基于交互作用的多变量灰色预测模型及其应用

丁 松, 党耀国, 徐 宁, 王俊杰

(1. 南京航空航天大学经济与管理学院, 江苏 南京 211106; 2. 滑铁卢大学系统设计工程系, 安大略 滑铁卢 N2L 3G1; 3. 南京审计大学管理科学与工程学院, 江苏 南京 211815)

0 引 言

多变量灰色预测模型是灰色系统理论中最重要的模型之一,该模型包含了一个系统行为特征序列和N-1个影响因子(又称驱动因素)序列,通过将已知因素作为驱动项和将未知因素作为灰作用量,建立微分方程描述驱动因素、灰作用量与系统行为间的关系,对系统行为进行预测。多变量灰色预测模型能够相对准确地描述系统与因素之间的关系,更符合灰色系统“部分信息已知,部分信息未知”的“小样本”“贫信息”不确定性系统结构特征。因此,该模型一直受到众多学者的关注。文献[1]提出了把驱动项作为灰常量来处理的思路,解决了传统GM(1,N)模型的模拟预测问题,并获得了广泛应用。文献[2]利用灰色关联度探讨了GM(1,N)模型的拟合度与变量的选择关系,说明变量选择在灰色模型建模过程中的重要性。文献[3]将自记忆性准则融入到多变量模型构建中,提出了SMGM(1,m)模型。文献[4]利用采样定理和状态转移矩阵分析了GM(1,N)模型差分方程和微分方程的关系,探索该模型的离散化结构解。文献[5]对传统模型的背景值进行了优化,并利用遗传算法对参数进行求解,提升了模型的适应能力。文献[6]利用非线性优化方法对GM(1,N)模型进行了拓展研究,结合BP神经网络进行优化求解,取得较好的应用效果。文献[7]对传统模型的背景值和残差进行了优化,使得新模型能够适应多种建模序列,丰富了灰色建模理论。文献[8]构建了新型GMC(1,N)模型,利用非线性优化技术进行参数估计,进一步提升模型的可靠性和适应性。文献[9]将系统变化趋势融入到GM(1,N)建模,使得新模型具有更强的适应能力和外推能力,进一步提升了模型对小样本系统的管控能力。

为了进一步改善模型的建模预测效果,提升传统GM(1,N)的适应能力和可靠性,许多学者从模型结构、参数估计、融合其他方法等角度开展了研究,已经取得一系列有价值的应用成果。文献[10]将影响因素的变化趋势融入到传统模型建模,构建了TGM(1,N)模型。文献[11]分析了传统模型的缺陷,并通过引入线性修正项和灰作用量项,构建了较为合理的建模过程和结构,并在实例中证明了其有效性和实用性。文献[12]对该新模型的性质进行了拓展研究,并利用该模型对北京市机动车数量进行了预测。文献[13]针对传统模型背景值选取存在的问题,构建含有插值系数的背景值,并利用遗传方法对参数进行估计,取得了较好的建模效果。文献[14]提出了反向累加多变量预测模型,并结合滚动机理对金砖国家的CO2排放量与能源消费、城市人口和经济增长的关系进行了系统分析和预测。文献[15]充分利用卷积积分技术的优势,提出了GMC(1,N)模型。文献[16-17]针对多种应用场景,提出了两种改进模型,拓展了GMC(1,N)模型的应用领域。文献[18]基于索洛余值法提出了FDGM(1,h)模型,并给出了反馈控制方程和参数估计方法。纵观以上文献可知,其对传统模型改进和拓展的方面还是以系统行为特征序列和驱动因素序列同期变化为基础。

另外,对于多变量系统的建模预测,其影响因素对系统行为特征序列产生作用效果可能会存在一定时滞现象,例如从城市交通拥堵到环境污染的产生、从科技投入到产出等均存在延迟。针对这类问题,一些学者也进行了研究。文献[19]针对输入和输出存在时滞现象的系统建模问题,构建了GM(1,N|τ,r)模型。文献[20]在此基础上利用分数阶累加算子,提出了基于分数阶累加的时滞GM(1,N,τ)模型。文献[21]将时滞控制因子引入到多变量离散模型的驱动因素控制项中,利用灰色扩维识别方法和灰色关联分析工具研究时滞参数的估计,具有十分重要的研究意义。文献[22]从时滞累积角度研究相关因素对主系统行为序列的累积影响效果,构建了时滞GM(1,N)的基本模型和拓展模型。

上述模型的改进与拓展在很大程度上提升了GM(1,N)模型的建模精度和动态预测能力,但考察多变量灰色预测模型的研究现状可以发现,现有模型往往只考虑了多个驱动因素对系统的独立影响,而忽略了多个因素之间的相互作用对系统特征的影响。事实上,两个系统影响因素同时作为驱动变量时,某一因素的变化会影响另外一因素对系统的作用,它们之间存在相互制约、相互依赖的关系。如对于高新技术企业产出而言,研究人力和研究经费投入是企业持续发展的基本动力,两者之间有着密不可分的交互关系；对于研究人力投入而言,其对企业产值的影响依赖研究经费的持续投入来保障研究人员的全身心投入;对于研究经费投入而言,其对企业产值的影响受到研究人员的调控。再如,CO2的排放量受到GDP增长和能源使用量的影响,一方面GDP的增长受能源使用量的制约,另一方面能源使用量的需求来源于GDP的增长,两者之间有着相互调控的作用,这类实例在经济生活中还有很多。因此,两者之间的交互关系需要引入模型的构建当中去。本文在对传统多变量模型基本原理研究的基础上,不仅考虑各影响因素的独立作用效果,还将它们之间的交互作用项引入模型构建当中去,针对不同数据特征,构建基于交互作用的GM(1,N)模型,最后通过案例说明本文建模的有效性。

1 传统GM(1,N)缺陷分析及交互作用内涵

1.1 传统GM(1,N)模型构建及缺陷分析

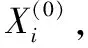
(1)

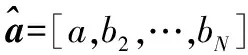
(2)

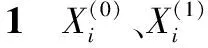
则参数列的最小二乘法估计满足:

证毕

1.2 交互作用的内涵

交互作用,反应的是两个或两个以上影响因素变量之间相互依赖、相互制约,共同对主系统变量的变化产生影响。当某影响因素对系统行为的作用效应的大小会因另一个影响因素的水平不同而有所差异时,则表示两个影响因素之间存在交互作用。常用的处理交互作用的方法是使用乘积项,可以通过以下简单的代数方程展现交互项的内在逻辑。若E(X1)表示系统行为特征序列,驱动因素用X2,X3表示,则传统独立的双因素灰色预测模型可以表示为

E(X1)=β1X2+β2X3+β4

(3)

如果驱动因素X2对系统的影响通过式(3)中的驱动系数β1来反映,且被认为驱动因素X3在X2对系统行为施加影响时有调节作用,那么当X2发生变化时,β1的取值也会产生相应的变化,通常情况下用线性方程说明X3对β1产生的影响,即β1=β3X3+α,则将该式代入式(3)并变形后,可得到包含乘积项的交互作用模型，即

E(X1)=β1X2+β2X3+β3X2X3+β4

(4)

式中,E(X1)表示系统行为特征序列,β3X2X3为交互作用项。当交互作用项为零时,表明X2和X3独立对系统行为序列产生影响,两影响因素不存在交互作用,反之则存在交互作用,如图1所示。

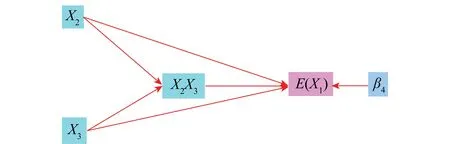
图1 两因素的交互作用示意图Fig.1 Schematic diagram of interaction between two factors

由图1可知，上述逻辑阐述过程过于简单,因为其他类型的交互模型会产生同样的方程,而其他类型的交互模型可以从不同的交互方程中演化而来。在此,本文仅给读者提供乘积项表示交互作用的背后逻辑,反映两个驱动因素间的双向线性调节作用。当然,在实际应用中,涉及驱动因素变量的可能函数关系也可能是非线性的,理想的函数形式应当通过数据分析驱动因素间的内在调节机理,构建适当的调节方程来反映因素间的交互关系对主系统行为的影响。

另外,也可能会存在3个及以上驱动因素间存在交互影响关系,需要进一步提炼交互驱动项。3个及以上驱动因素间的交互关系,除了两两因素间的双向交互作用,还存在三向交互作用,甚至多向交互作用,此类交互项形式往往可使用乘积项的多项式表示。以三向交互作用为例,其交互形式为

E(X1)=β1X2+β2X3+β3X3+β4X2X3+

β5X3X4+β6X2X4+β7X2X3X4+β8

(5)

可见,三因素间的交互作用更加复杂,包括主效应、双向交互作用和三向交互作用,分别由3个驱动因素自身(X2,X3,X4)、成对项(X2X3,X3X4,X2X4)、共同的乘积项(X2X3X4)表示。三向交互作用的显著性主要由共同乘积项体现,若β7=0,则不存在三向交互作用,该模型则退化为上文中的双向交互作用模型。对于4个及以上因素的交互作用,采用类似的推理方式,模型结构形式将更加复杂。

对于交互作用的识别,在经典的统计学研究里,交互作用的识别是通过F检验或者标准t检验来推断两影响因素间的交互效应是否显著,进而判断是否需要引入交互作用项,而统计建模的最大特点就是大样本大数据,这一点在现实生活中存在的“贫信息,小样本”数据类型则不太适用。因此,本文依据交互作用的现实含义,通过专家经验分析并利用灰色系统理论中的灰色关联分析方法对两个相关因素间的逻辑关系加以研究,确定驱动因素间是否存在交互作用关系。

2 基于交互作用的IEGM(1,N)模型构建及参数求解

2.1 基于交互作用的IEGM(1,N)模型构建

为了能够有效解决传统模型没有考虑交互作用项的缺陷,将影响因素的交互作用项引入经典GM(1,N)模型的灰作用量,构建基于交互作用的IEGM(1,N)(interaction effect grey model ofNvariables)模型及其拓展模型,以反映不同输入变量间的交互作用关系对系统行为变量的影响,并通过江苏省高新技术产业产值的案例分析,验证本文模型的有效性和实用性。

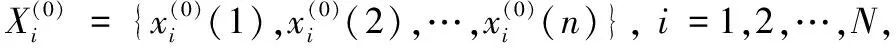
(6)

为基于交互作用的GM(1,N)模型,记为IEGM(1,N)

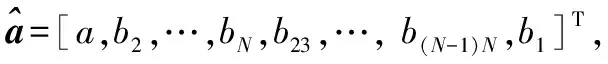
(7)

为IEGM(1,N)模型的白化微分方程。

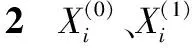
则参数列的最小二乘法估计满足:

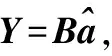
证毕

在估计出参数列之后,可以参照文献[1]中GM(1,N)求解过程,对IEGM(1,N)模型进行求解,便可得到以下求解步骤。

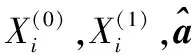
(1) 白化方程(7)的解为

(8)

(2) 当驱动项及交互项变化幅度很小时,可视驱动项和交互项为灰常量,则IEGM(1,N)模型的近似时间响应式为

(9)

(3) 累减还原式为

(10)

(4) IEGM(1,N)差分模拟式为

(11)

证明(1)由白化微分方程(7)可得通解公式为

(12)

(13)

再将式(13)代入式(12)便可得到式(9),定理得证。

证毕

式(2)～式(4)将驱动项和交互项看作灰常量,类似看成是GM(1,1)模型证明过程便可得证。

定理2和定理3分别给出了IEGM(1,N)模型参数估计和模拟值计算公式,当主系统行为和驱动因素交互项作用机制已知时,便可通过上述定理进行计算。

2.2 基于交互作用的IEGM(1,N)模型的拓展模型

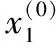
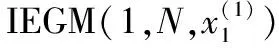
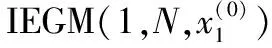
其中

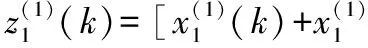
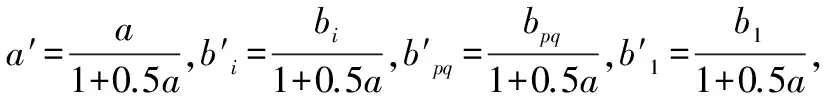
(14)

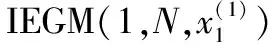
其中

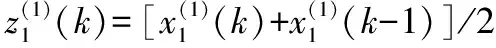
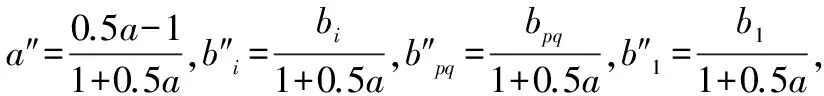
(15)

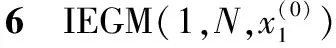
证明由定理4和定理5的证明过程可知,这3种模型均是在经典建模的基础上,代入背景值和累减还原公式进行化简得到,它们之间可以相互转化推导,因此是等价的。

3 案例分析

高新技术产业是提升国家创新能力的重要载体,是国家之间经济、科技竞争的制高点,代表了国家未来技术与产业的发展方向。从高新技术产业本身来看,人力投入和经费投入是创新产出的重要影响因素,它们之间相互影响、相互制约。在人力资本投入方面,科技人才是高新技术产业持续发展的基本动力,拥有高质量的科技人才和高规模的人力投入,才能保证企业研发创新活动的高效持续进行,进而提升企业创新产出,而人才投入多少,对产业产值贡献度的大小受到资金投入的调节作用。在资金投入方面,研发经费投入能够反映高新技术产业研发创新的基础能力和潜在产出,并为高新技术产业研发创新活动的顺利完成提供基础保障,但资金效益的产生依赖人才优势的发挥。因此,从经验分析角度看,增加和合理利用科技人员和研发经费,明晰两者间的交互作用关系,会直接促进高新技术产业产值的增加,提升高新技术产业的创新产出。

为了能验证本文模型在实际应用中的有效性,拟通过多种模型的对比分析,对江苏省高新技术产业产值进行预测分析。江苏省十分重视高新技术产业的发展,近些年对该产业的发展投入了大量的精力,主要包括科技人员投入和研发经费投入。在变量选择方面,本文以我国高新技术产业产值为产出指标(系统行为变量),以科技活动人员数(万人)和研发经费内部支出(亿元)为投入指标(驱动因素变量),2005-2015年这3个指标的数据如表1所示，其数据来源于江苏省统计年鉴和2015年江苏省高新技术产业主要数据统计公报。

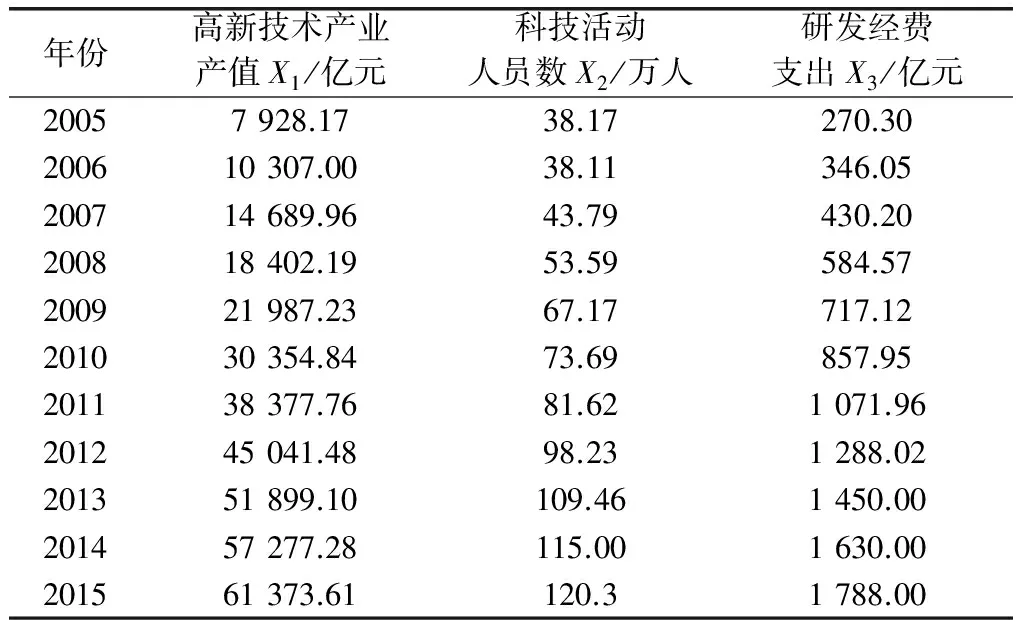
表1 江苏省高新技术产业产值及影响因素

为了避免不同数量级、量纲给模型带来病态性误差,本文将原始数据进行初值化,并在现价的基础上,计算出3种变量的增长速度,结果如表2所示。

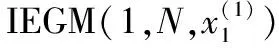
由表3中4种模型计算结果可知,传统GM(1,N)的平均相对误差高达33.01%,其两步外推误差也高达25.71%,已经基本失去模拟和预测的意义。产生那么大误差的主要原因是驱动因素变化幅度较大,不满足作为灰常量的建模基础,而且该模型没有考虑到人员投入与资金投入之间的交互作用关系,因此传统模型模拟和预测效果不理想。为了作为参照,本文还将GM(1,1)模型用于高新技术产值的单变量建模,基于模拟效果还不错,误差为6.25%,但是不能保证具有较好的外推效果,两步外推平均误差高达27.51%,主要是因为GM(1,1)仅适用于低速增长的准指数序列建模,对于波动增长序列建模效果较差。

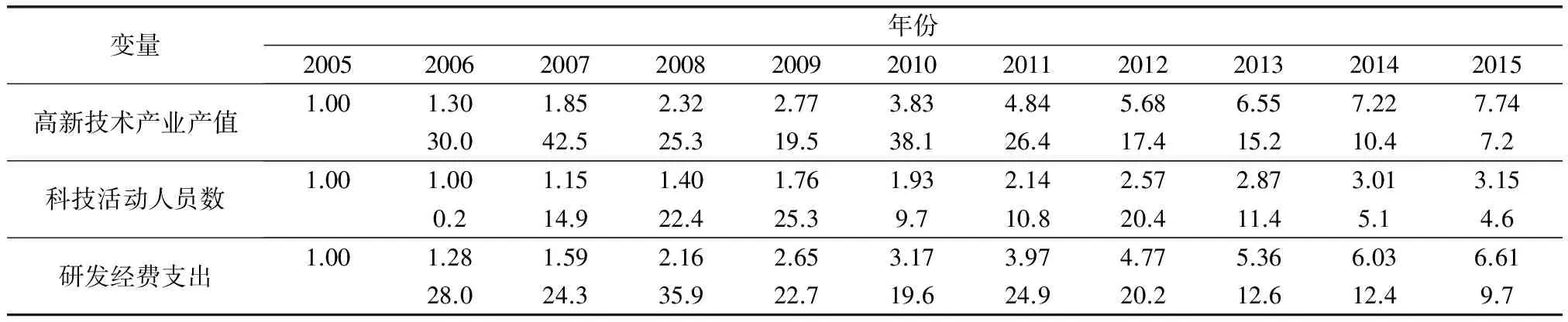
表2 各变量初值化后的数值增长速度

表3 各种模型模拟和预测结果

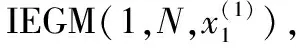
则关联度计算公式为

4 结 论

[1] 刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京:科学出版社,2010:149-157.

LIU S F, DANG Y G, FANG Z G. Grey system theory and its application[M]. Beijing: Science Press, 2010: 149-157.

[2] 尹子民,罗丽兮.灰色模型GM(1,n)的变量选择及拟合度分析[J].系统工程理论与实践,1999,19(11): 81-83.

YIN Z M, LUO L X. Variable selection and error analyzing of GM(1,n)[J]. Systems Engineering-Theory & Practice, 1999, 19(11): 81-83.

[3] GUO X J, LIU S F, WU L F, et al. A multi-variable grey model with a self-memory component and its application on engineering prediction[J]. Engineering Applications of Artificial Intelligence, 2015, 42(C): 82-93.

[4] 仇伟杰, 刘思峰. GM(1,N)模型的离散化结构解[J]. 系统工程与电子技术, 2006, 28(11): 1679-1681.

QIU W J, LIU S F. Dispersed structure solve of model GM(1,N)[J]. Systems Engineering and Electronics, 2006, 28(11): 1679-1681.

[5] PEI L L, CHEN W M, BAI J, et al. The improved GM (1,N) models with optimal background values: a case study of Chinese high-tech industry[J].The Journal of Grey System,2015,27(3): 223-234.

[6] 周伟, 方志耕. 非线性优化GM(1,N)模型及其应用研究[J]. 系统工程与电子技术, 2010, 32(2):317-320.

ZHOU W, FANG Z G. Nonlinear optimization method of model GM(1,N) and application[J]. Systems Engineering and Electronics,2010, 32(2): 317-320.

[7] GUO H, XIAO X P, FORREST J. A research on a comprehensive adaptive grey prediction model CAGM(1,N)[J]. Applied Mathematics and Computation, 2013, 225(1): 216-227.

[8] WANG Z X, HAO P. An improved grey multivariable model for predicting industrial energy consumption in China[J]. Applied Mathematical Modelling, 2016, 40(11): 5745-5758.

[9] DING S, DANG Y G, LI X M, et al. Forecasting Chinese CO2emissions from fuel combustion using a novel grey multivariable model[J].Journal of Cleaner Production,2017,162:1527-1538.

[10] 丁松, 党耀国, 徐宁. 基于驱动变量增长趋势的TGM(1,N)预测模型[J]. 系统工程, 2015, 33(3): 149-153.

DING S, DANG Y G, XU N. TGM(1,N) prediction model based on trends of driving variables[J]. Systems Engineering, 2015, 33(3): 149-153.

[11] ZENG B, LUO C, LIU S, et al. Development of an optimization method for the model GM (1,N)[J]. Engineering Applications of Artificial Intelligence, 2016, 55: 353-362.

[12] ZENG B, LUO C, LIU S, et al. A novel multi-variable grey forecasting model and its application in forecasting the amount of motor vehicles in Beijing[J]. Computers & Industrial Engineering, 2016, 101(C): 479-489.

[13] HSU L C. Forecasting the output of integrated circuit industry using genetic algorithm based multivariable grey optimization models[J].Expert Systems with Applications, 2009, 36(4): 7898-7903.

[14] WU L, LIU S, LIU D, et al. Modelling and forecasting CO2 emissions in the BRICS (Brazil, Russia, India, China, and South Africa) countries using a novel multi-variable grey model[J]. Energy, 2015, 79(79): 489-495.

[15] TIEN T L. The indirect measurement of tensile strength of material by the grey prediction model GMC(1,N)[J]. Measurement Science Technology 2005, 16(6): 1322-1328.

[16] TIEN T L. Forecasting CO2 output from gas furnace by grey prediction model IGMC(1,N)[J]. Journal of the Chinese Society of Mechanical Engineers, 2010, 31(1): 55-65.

[17] TIEN T L. The indirect measurement of tensile strength by the new model FGMC(1,N)[J]. Measurement, 2011, 44(10):1884-1897.

[18] XIE N M, ZHU C Y, ZHENG J. Expansion modelling of discrete grey model based on multi-factor information aggregation[J]. Journal of Systems Engineering and Electronics, 2014, 25(5): 833-839.

[19] 黄继.灰色多变量GM(1,N|τ,r)模型及其粒子群优化算法[J].系统工程理论与实践,2009, 29(10):145-151.

HUANG J. Grey GM(1,N|τ,r) model and its particle swarm optimization algorithm[J].Systems Engineering-Theory & Practice, 2009, 29(10): 145-151.

[20] 毛树华,高明运,肖新平. 分数阶累加时滞GM(1,N,τ)模型及其应用[J]. 系统工程理论与实践, 2015, 35(2):430-436.

MAO S H, GAO M Y, XIAO X P. Fractional order accumulation time-lag GM(1,N,τ) model and its application[J]. Systems Engineering-Theory & Practice, 2015, 35(2): 430-436.

[21] 张可,曲品品,张隐桃.时滞多变量离散灰色模型及其应用[J].系统工程理论与实践,2015,35(8): 2092-2103.

ZHANG K, QU P P, ZHANG Y T. Delay multi-variables discrete grey model and its application[J]. Systems Engineering-Theory & Practice, 2015, 35(8): 2092-2103.

[22] 王正新. 多变量时滞GM(1,N)模型及其应用[J]. 控制与决策, 2015, 30(12):2298-2304.

WANG Z X. Multivariable time-delayed GM(1,N) model and its application[J]. Control and Decision, 2015, 30(12): 2298-2304.