基于模糊多目标规划的防空反导火力分配

徐 浩, 邢清华, 王 伟

(空军工程大学防空反导学院, 陕西 西安 710051)

0 引 言

信息化条件下,空袭是高度集成的体系化作战。作为防御方,需要同时执行防空和反导任务,即利用防空反导武器系统担负起同时反空气动力学目标和反弹道类目标的作战任务[1]。火力分配(weapon target assignment,WTA)作为防空反导作战的关键环节,对防空反导作战效能的发挥具有重要影响。因此研究防空反导WTA具有非常重要的意义。

鉴于WTA的重要性,广大学者纷纷采用蚁群算法[2]、遗传算法[3]、克隆选择算法[4]、Memetic 算法[5]和粒子群算法[6]等对WTA问题进行了深入研究。这些研究大多以对敌毁伤概率最大为目标函数构建单目标优化WTA模型,需要分配全部火力,不符合作战实际。为此,文献[5-6]提出以最大作战效费比为目标函数构建WTA模型,避免分配全部火力。然而,这种方法本质上还是单目标优化,采用事先提供的决策偏好信息,仅能给出一种WTA方案,对战场态势变化的适应性较弱和对不同指挥员的决策偏好体现不够。并且,随着战场环境的日益复杂化,防空反导作战过程中获取的信息具有很强的不确定性,确定型WTA方法[2,6]已很难适用。

为此,考虑到基于多目标优化的WTA方法[7-8]能提供多种分配方案,具有对战场态势变化适应性较强和能较好地融合指挥员决策偏好的优点,并针对防空反导WTA面临目标威胁信息不确定的情况,采用模糊多目标规划方法构建WTA模型以提高不确定情况下防空反导WTA方法对战场态势变化的适应性。鉴于量子行为粒子群算法的优良性能,提出具有单/双势阱的多目标量子行为粒子群算法(multi-objective quantum-behaved particle swarm optimization with double/single-well, MOQPSO-D/S)以求解所建立的WTA模型。

1 基于模糊多目标规划的防空反导WTA建模

1.1 模型假设

假设m个防空反导武器系统参与作战,需要拦截n个来袭目标,其中,第1～na个目标为空气动力学目标,记为A类目标,其余为弹道类目标,记为B类目标。

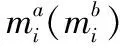
假设第i个武器系统发射xij枚拦截弹拦截第j个目标,且单发毁伤概率为pij。

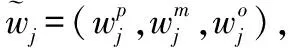
1.2 模糊多目标建模

以拦截效益最大化和拦截损耗最小化为目标建立多目标火力分配优化模型

(1)

(2)

约束条件为

(1) 武器系统i最多射击一种类型的目标

(3)

(2) 武器系统i拦截的目标数量不能多于其目标通道

(4)

(3) 武器系统i发射的拦截弹数量不能多于其导弹通道

(5)

(4) 武器系统i发射的拦截弹数量不能多于其携带的导弹数量

(6)

(5) 用于拦截目标j的拦截弹数量不少于拦截其所需的最少火力

(7)

1.3 模型的等价清晰化

该WTA模型的目标函数含有模糊参数,不能直接采用优化算法对其进行求解,需要对含有模糊参数的目标函数进行处理,转化为相应的清晰等价形式。

利用不确定理论中的必要性测度[9]将含有模糊参数的目标函数式(1)转化为

minc

(8)

式中,θ为来袭目标剩余威胁度小于或等于c的必要性测度。

因此，可以将式(8)转化为

minc

(9)

进一步得到其清晰等价形式

(10)

这样将基于模糊多目标规划的WTA模型转化为了清晰的多目标规划模型,可以利用多目标优化算法对其进行求解。

2 基于MOQPSO-D/S的模型求解

量子行为粒子群算法[10](quantum-behaved particle swarm optimization,QPSO)相对粒子群算法具有收敛速度更快、控制参数更少和全局收敛等优点,已受到广大学者关注[11-12]。起初,QPSO主要用于求解单目标优化问题。后来,学者们将其引入到多目标优化问题中,提出了多种基于QPSO的多目标优化算法[13-17]。鉴于这类算法的优良性能,将其引入到WTA多目标优化问题的求解中。

2.1 MOQPSO-D/S算法

多目标优化不同于单目标优化收敛于一个全局最优解,它要求解集多样性要好、分布均匀、与真实Pareto解集尽可能接近。然而,QPSO的快速收敛特性,导致基于QPSO的多目标优化算法具有容易早熟收敛的缺陷;QPSO全局收敛于一个最优解的特性又限制了基于QPSO的多目标优化算法解的多样性和分布性。为此,提出MOQPSO-D/S算法用于求解防空反导WTA多目标规划模型。该算法采用单/双势阱粒子位置更新方法均衡解的多样性、求解精度及速度之间的关系;采用混合随机变异方法避免算法早熟收敛及提高算法整体寻优精度;采用两阶段法选取领导粒子,提高解的分布均匀性和求解速度。

2.1.1 单/双势阱粒子位置更新公式

所谓单/双势阱位置更新方法就是在寻优早期,为提高种群多样性和避免算法早熟收敛,采用两个吸引子来更新粒子的位置;在寻优后期,为提高算法收敛精度和速度,采用单个吸引子来更新粒子的位置。具体的位置更新公式为

xk(t+1)=

(11)

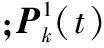
(12)

Lk(t)=

(13)

式中,α是扩张-收缩因子。

2.1.2 粒子混合随机变异方法

为了避免算法在寻优早期出现早熟收敛以及提高算法在寻优后期的收敛精度,提出混合随机变异方法。所谓混合随机变异,就是在寻优早期采用均匀随机变异,在寻优后期采用高斯变异。均匀随机变异可以使粒子以等概率在[xmin,xmax]上完全遍历,从而可以提高解的多样性,避免算法早熟收敛。其中[xmin,xmax]是决策变量的优化取值范围。高斯变异可以使粒子在原位置附近变异,从而避免算法后期因变异范围过大而导致寻优倒退,同时可以提高算法后期的局部寻优精度。具体方法为

(15)

式中,rand是闭区间[0,1]上均匀分布的随机数;Rand(·)是均匀随机变异算子;Gaussian(·)是高斯变异算子;σ是高斯变异均方差;pm是变异概率。

2.1.3 两阶段领导粒子选取方法

(16)

式中,x是粒子的位置；Nf是目标函数的个数。

sigma值法选择领导粒子的原理如图1所示。

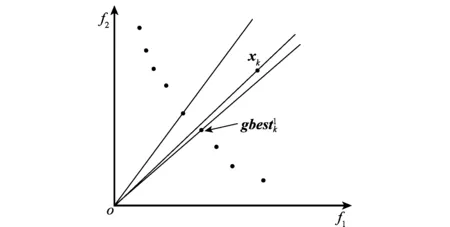
图1 Sigma值法选择领导粒子Fig.1 Selection guider particle by sigma method

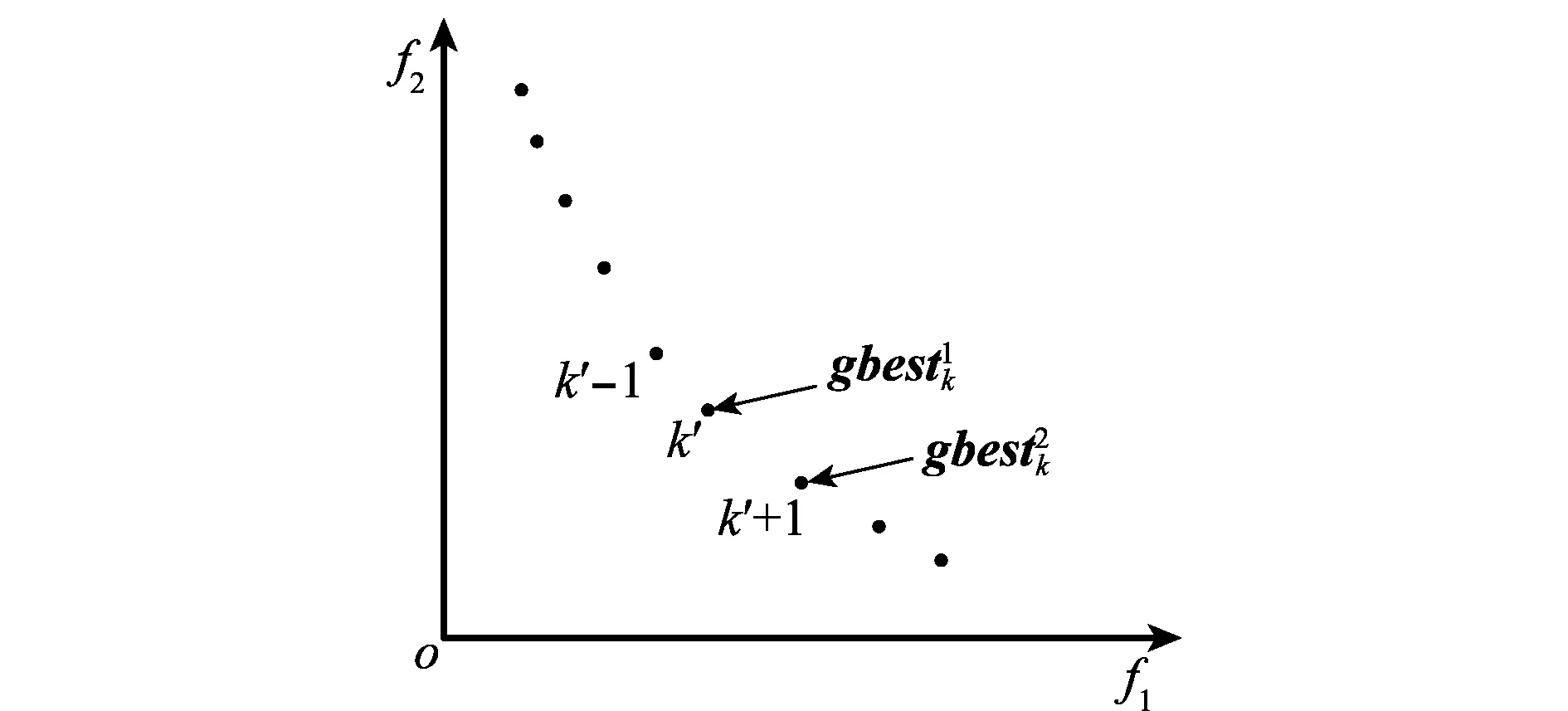
图2 第2个领导粒子的选取方法Fig.2 Selection method of the second guider particle

2.2 MOQPSO-D/S算法求解WTA模型

2.2.1 粒子编码

由于MOQPSO-D/S算法不能直接求解离散问题,因此需要对粒子的位置进行编码才能求解WTA模型。记粒子位置为x,采用矩阵式编码方式进行编码,具体为

式中,xij表示武器系统i拦截目标j所使用的拦截弹数量。

2.2.2 基于MOQPSO-D/S的模型求解过程

基于MOQPSO-D/S算法求解防空反导WTA模糊规划模型的具体步骤如下:

步骤1设置算法参数,随机初始化种群。

步骤3初始化外部存储文件ARCHIVE。根据粒子的适应度计算粒子间的支配关系;将非支配粒子存储到ARCHIVE中,并计算ARCHIVE中粒子的拥挤距离和sigma值。

步骤4令迭代次数t=1。

步骤5采用两阶段法选择各粒子的领导粒子gbest1和gbest2(当t>tmax/2时,不选取gbest2),并按式(11)更新粒子位置。

步骤6判断是否满足变异条件。若满足,则对粒子进行混合随机变异操作;否则转步骤7。

步骤8计算粒子xk与ARCHIVE中粒子的支配关系,若粒子xk支配ARCHIVE中的粒子xg,则将粒子xk加入ARCHIVE中,并删除粒子xg;若粒子xk与ARCHIVE中的粒子互不支配,则将粒子xk加入ARCHIVE中,转步骤9;否则,转步骤10。

步骤9计算更新后ARCHIVE中粒子的拥挤距离及新加入粒子的sigma值;判断ARCHIVE中的粒子数是否超过容量,若超出容量,则将拥挤距离最小的粒子删除;否则转步骤10。

步骤10令t=t+1;判断t>tmax是否成立,若成立,则终止迭代,输出ARCHIVE中的粒子作为多个防空反导WTA方案;否则转步骤5。

2.3 MOQPSO-D/S算法的计算复杂度分析

设群体规模为N,ARCHIVE容量为M,目标函数个数为Nf,则MOQPSO-D/S算法单次迭代的计算复杂度主要由以下几部分决定:计算各粒子适应度的计算复杂度O(NfN);粒子个体最优位置更新的计算复杂度O(NfN);种群位置更新后,各粒子与ARCHIVE中的粒子进行比较的计算复杂度O(NfMN);更新ARCHIVE,进行拥挤距离排序的计算复杂度O(Nf(M+N)2);计算更新后ARCHIVE中粒子的sigma值的计算复杂度为O(N)。以上都是各部分最差情况下的计算复杂度。因此,MOQPSO-D/S算法每进行一次迭代的计算复杂度为O(Nf(M+N)2)。这与文献[15]中给出的MOQPSO-CD的计算复杂度是相同的,在可接受范围内。

3 实例分析

为了验证基于模糊多目标规划的火力分配模型的合理性,同时考察MOQPSO-D/S算法求解火力分配问题的寻优性能,给出以下实例。

假设某次防空反导作战中,我方6个武器系统Wi(i=1,2,…,6)需要拦截5个来袭目标Tj(j=1,2,…,5)。各武器系统所拥有的目标通道、导弹通道、弹药库存量以及单发拦截弹的归一化价值如表1所示。

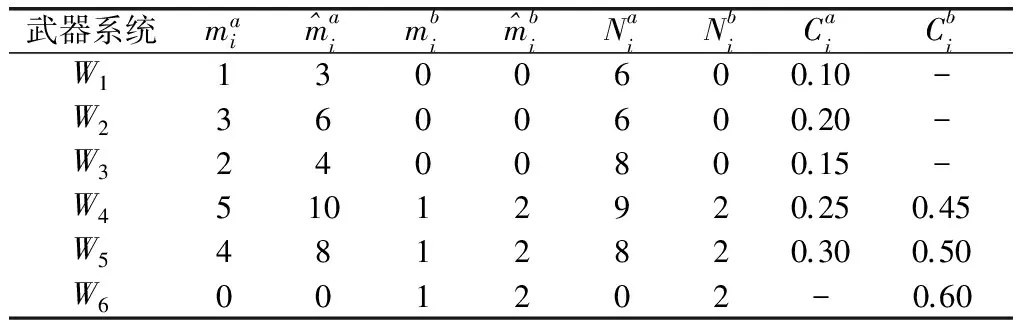
表1 各武器系统的WTA及拦截弹价值

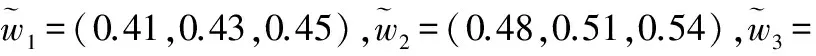
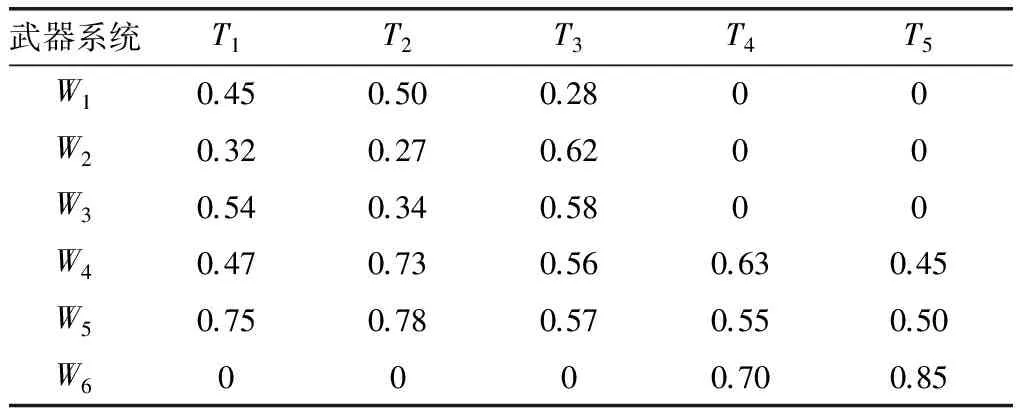
表2 单发毁伤概率

在Core i5 3.3 GHz、内存4 GB的计算机上的Matlab 2013a环境下进行仿真实验。以单目标优化算法IDPSO[6],以及MOQPSO-DPS[17]、MOQPSO-CD[14]和MOPSO-CD[20]等多目标优化算法作为对比算法,与本文提出的MOQPSO-D/S在求解WTA问题上进行性能对比。各算法均采用相同的粒子编码和不可行解调整方式,多目标优化算法的ARCHIVE容量都设置为100, MOQPSO-D/S、MOQPSO-DPS和MOQPSO-CD算法的扩张-收缩因子α随着迭代次数变化由1呈线性递减到0.4。

3.1 实时性分析

在不同群体规模和迭代次数下采用MOQPSO-D/S算法求解算例,分别运行30次,算法平均运行时间如表3所示。

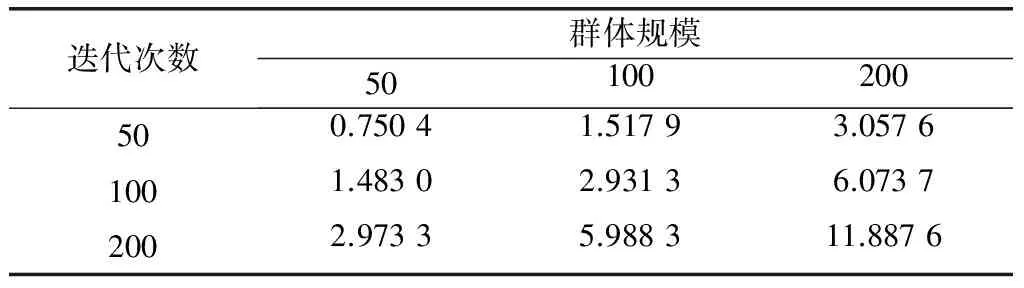
表3 算法平均运行时间

由表3可知,MOQPSO-D/S算法可以有效满足防空反导WTA对算法实时性的需要。

在群体规模和迭代次数都为100的情况下,采用MOQPSO-DPS、MOQPSO-CD和MOPSO-CD求解算例,分别运行30次,将它们的运行时间与本文算法相对比,结果如图3所示。

图3 各算法的实时性比较Fig.3 Comparison of real-time performance

由图3可知,MOQPSO-D/S的实时性要明显优于其他3种算法。

3.2 收敛性分析

采用MOQPSO-D/S求解算例,在群体规模和迭代次数都为50的情况下,获得的结果如图4所示。

图4 MOQPSO-D/S求解算例的仿真结果Fig.4 Simulation results of MOQPSO-D/S solving the example

由图4可知,采用MOQPSO-D/S求解防空反导WTA的模糊多目标规划模型得到的解,分布较为均匀。其中,每个点对应一种WTA方案,可以为指挥员提供多种决策方案。指挥员根据战场态势和风险偏好做出最终的WTA决策。相较于仅能给出WTA方案的单目标优化方法,该方法可以更好地适应战场态势的变化和融合指挥员战术思想来进行WTA。

为了验证采用MOQPSO-D/S求解WTA问题得到的结果的有效性,采用文献[6]中以最大效费比为目标函数建立的单目标WTA模型和IDPSO算法求解本算例。设置群体规模和迭代次数均为50,进行30次仿真,平均运行时间为0.719 3 s,算法的迭代曲线和最优WTA结果分别如图5和表4所示。

图5 基于IDPSO的WTA迭代曲线Fig.5 Iterative curve of WTA based on IDPSO

由图5可知，单目标优化算法所得到的最优分配结果与图4中红色五角星标注点对应结果相同,而算法在相同群体规模和迭代次数条件下的平均运行时间比MOQPSO-D/S算法略小。由此表明,虽然采用MOQPSO-D/S求解WTA问题一定程度上分散了计算资源,但依然能获得包含单目标最优分配结果的满意结果。同时证明了基于模糊多目标规划的WTA模型是合理的,采用MOQPSO-D/S求解模型是可行的。

表4 基于IDPSO的最优WTA

为了进一步验证MOQPSO-D/S算法求解WTA问题时的收敛性,在群体规模和迭代次数都为100的条件下,采用MOQPSO-D/S、MOQPSO-DPS、MOQPSO-CD和MOPSO-CD求解算例,将得到的Pareto最优解集进行对比。以支配覆盖率C(X1,X2)[21]衡量各算法的收敛性优劣。其中,X1和X2分别表示两种算法得到的Pareto最优解集,C(X1,X2)越大、C(X2,X1)越小,表明X1对应算法的收敛性能越优于X2对应算法。各算法的对比结果如表5所示,表中A1,A2,A3和A4分别代表MOQPSO-D/S、MOQPSO-DPS、MOQPSO-CD和MOPSO-CD算法所求得的Pareto最优解集。

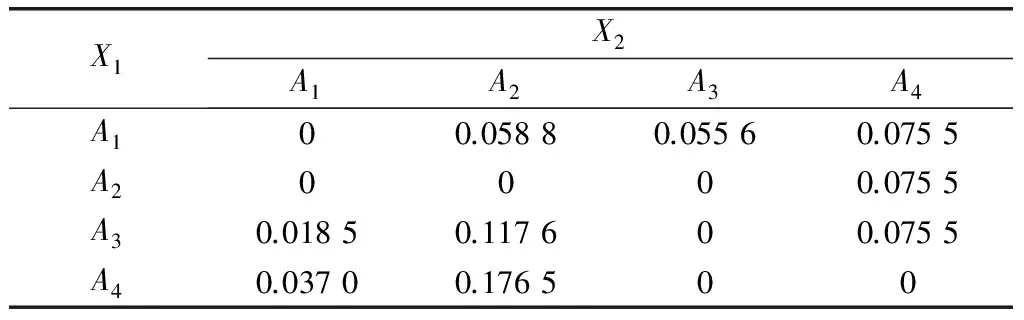
表5 各算法的Pareto最优解集之间的支配覆盖率

由表5可知,MOQPSO-D/S求解WTA问题的收敛性与其他3种多目标优化算法相比是最好的。

3.3 多样性分析

为了验证MOQPSO-D/S算法求解WTA问题得到的Pareto解的分布均匀性,采用分布广度指标SP[22]进行评价,SP值越小,表明Pareto解分布越均匀。在群体规模和迭代次数都为100的条件下,算法均独立运行30次,SP值的统计结果如图6所示。

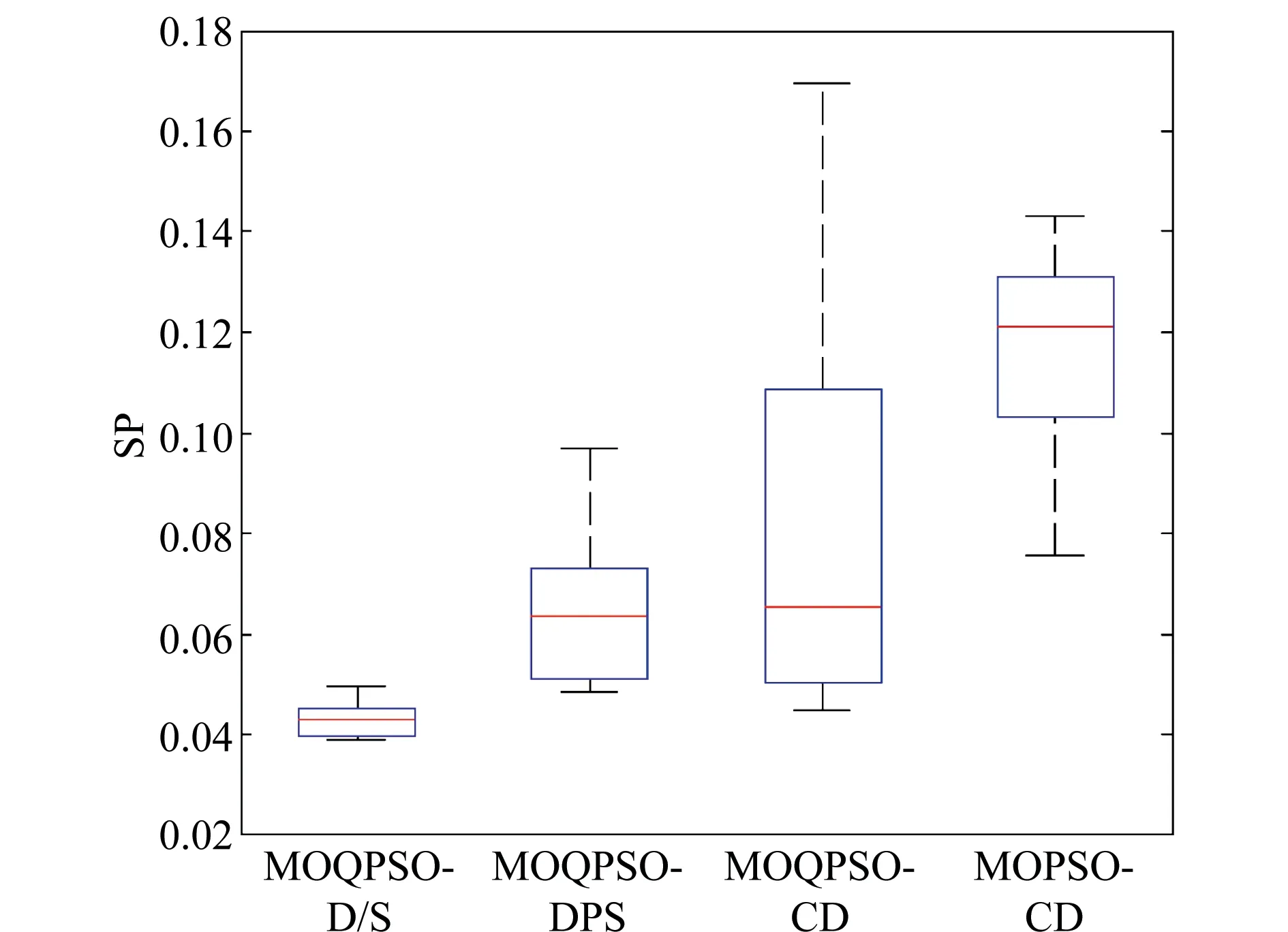
图6 各算法的Pareto最优解集的分布性Fig.6 Diversification of four algorithms’ Pareto optimal sets

由图6可知,MOQPSO-D/S算法求解WTA问题得到的Pareto最优解集的分布是最均匀的,并且MOQPSO-D/S求得的 Pareto最优解集的分布性是最稳定的。

为了进一步验证MOQPSO-D/S算法求解防空反导WTA问题的有效性,在此对不同作战规模(m×n)算例进行仿真求解。各算法求解作战规模分别为6×6、20×30和50×80的算例,必要性测度均为0.8,进行30次仿真得到的仿真结果如表6所示。

表6 各算法求解不同作战规模算例的性能比较

由于篇幅所限,在此不一一列出各武器系统的火力配置及拦截弹价值、目标威胁度和单发毁伤概率。由表6可知,求解不同作战规模的算例时,MOQPSO-D/S算法在实时性及解的分布均匀性方面依然比其他3种算法优越。另外,通过采用支配覆盖率对比各算法所求得的Pareto最优解集可知, MOQPSO-D/S求解不同作战规模的WTA问题的收敛性依然是最好的。在此不再列出各算法所求Pareto最优解集之间的支配覆盖率。

4 结 论

基于模糊多目标规划方法建立的防空反导WTA模型,考虑了来袭目标威胁值不确定的问题,可以为不确定情况下的防空反导WTA提供参考。

基于MOQPSO-D/S的WTA方法可以得到多种WTA方案,相比单目标优化方法,在辅助WTA决策时,能更好地适应战场态势的变化及融合指挥员的战术思想。

由于采用了单/双势阱粒子位置更新、混合随机变异和两阶段领导粒子选取等方法,所提出的MOQPSO-D/S算法相比MOQPSO-DPS、MOQPSO-CD及MOPSO-CD算法,在求解WTA问题时,具有更好的实时性、收敛性以及可以获得分布更为均匀的Pareto最优解集,可以为WTA多目标优化模型的求解提供优良算法。

[1] TEAGUE J M, DORNER K R, HARTMAN W B. Back to the future: integrated air and missile defense in the pacific, AD-A622600[R].Maxwell AFB,AL:Air Force Research Institute,2015.

[2] 常天庆,陈军伟,郝娜,等.装甲分队动态武器目标分配中蚁群算法终止控制[J].系统工程与电子技术,2015,37(2):343-347.

CHANG T Q, CHEN J W, HAO N, et al. Terminating control of ant colony algorithm for armored unit[J].Systems Engineering and Electronics, 2015, 37(2): 336-342.

[3] 董朝阳,路遥,王青.改进的遗传算法求解火力分配优化问题[J].兵工学报,2016,37(1):97-102.

DONG C Y, LU Y, WANG Q. Improved genetic algorithm for solving firepower distribution[J]. Acta Armamentraii,2016,37(1):97-102.

[4] LIANG H, KANG F. Adaptive chaos parallel clonal selection algorithm for objective optimization in WTA application[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(6): 3459-3465.

[5] 颜冀,李相民,刘立佳,等.基于Memetic算法的超视距协同空战火力分配[J].北京航空航天大学学报,2014,40(10):1424-1429.

YAN J, LI X M, LIU L J, et al. Weapon-target assignment based on memetic optimization algorithm in beyond-visual-rang cooperative air combat[J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(10): 1424-1429.

[6] 范成礼, 邢清华, 郑明发, 等. 基于IDPSO的武器目标分配优化算法[J]. 系统工程与电子技术, 2015, 37(2): 336-342.

FAN C L, XING Q H, ZHENG M F, et al. Weapon-target allocation optimization algorithm based on IDPSO[J]. Systems Engineering and Electronics, 2015, 37(2): 336-342.

[7] 顾佼佼,赵建军,颜骥,等.基于MODPSO-GSA的协同空战武器目标分配[J].北京航空航天大学学报,2015,41(2):252-258.

GU J J, ZHAO J J, YAN J, et al. Cooperative weapon-target assignment based on multi-objective discrete particle swarm optimization-gravitational search algorithm in air combat[J]. Journal of Beijing University of Aeronautics and Astronautics,2015,41(2):252-258.

[8] 张滢,杨任农,左家亮,等.基于分解进化多目标优化算法的火力分配问题[J].系统工程与电子技术,2014,36(12):2435-2441.

ZHANG Y, YANG R N, ZUO J L, et al. Weapon-target assignment based on decomposition-based evolutionary multi-objective optimization algorithms[J]. Systems Engineering and Electronics, 2014, 36(12): 2435-2441.

[9] 刘宝碇, 赵瑞清, 王纲. 不确定规划及应用[M]. 北京: 清华大学出版社, 2003.

LIU B D, ZHAO R Q, WANG G. Uncertain programming with application[M]. Beijing: Tsinghua University Press, 2003.

[10] SUN J, FENG B, XU W B. Particle swarm optimization with particles having quantum behavior[C]∥Proc.of the IEEE Congress on Evolutionary Computation, 2004: 325-331.

[11] SINGH M R, MAHAPATRA S S. A quantum behaved particle swarm optimization for flexible job shop scheduling[J]. Computers & Industrial Engineering, 2016, 93(1): 36-44.

[12] WANG G G, GANDOMI A H, ALAVI A H, et al. A hybrid method based on krill herd and quantum-behaved particle swarm optimization[J]. Neural Computing and Applications, 2016, 27(4): 989-1006.

[13] 沈佳宁. 基于QPSO算法求解多目标优化问题及其应用[D]. 无锡: 江南大学, 2008.

SHEN J N. Solving multi-objective problem based on QPSO algorithm and application[D]. Wuxi: Southern Yangtze University, 2008.

[14] 施展, 陈庆伟. 基于QPSO和拥挤距离排序的多目标量子粒子群优化算法[J]. 控制与决策, 2011, 26(4): 540-547.

SHI Z, CHEN Q W. Multi-objective quantum-behaved particle swarm optimization algorithm based on QPSO and crowding distance sorting[J].Control and Decision,2011,26(4):540-547.

[15] 施展. 多目标量子行为粒子群优化算法研究[D]. 南京: 南京理工大学, 2011.

SHI Z. Research on multi-objective quantum-behaved particle swarm optimization algorithms[D]. Nanjing: Nanjing University of Science and Technology, 2011.

[16] HEYAM A B. A quantum behaved particle swarm approach to multi-objective optimization[D]. Birmingham, UK: the University of Birmingham, 2015.

[17] XU S H, MU X D, CHAI D, et al. Multi-objective quantum-behaved particle swarm optimization algorithm with double-potential well and share-learning[J]. Optik-International Journal for Light and Electron Optics, 2016, 127(12): 4921-4927.

[18] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-II[J]. IEEE Trans.on Evolutionary Computation, 2002, 6(2): 182-197.

[19] MOSTAGHIM S, TEICH J. Strategies for finding good local guides in multi-objective particle swarm optimization (MOPSO)[C]∥Proc.of the IEEE Swarm Intelligence Symposium, 2003: 26-33.

[20] RAQUEL C R, JR NAVAL P C. An effective use of crowding distance in multiobjective particle swarm optimization[C]∥Proc.of the Genetic and Evolutionary Computation Conference, 2005: 257-264.

[21] ZITZLER E. Evolutionary algorithms for multi-objective optimization methods and applications[D]. Switzerland: Swiss Federal Institute of Technology Zurich, 1999.

[22] SCHOTT J R. Fault tolerant design using single and multicriteria genetic algorithm optimization[D]. Cambridge: Massachusetts Institute Technology, 1995.