利用优化概率神经网络识别自相关过程异常

（昆明理工大学，昆明 650500）

0 引言

控制图是统计过程控制的基本工具和手段，经过不断发展有学者相继提出了两种控制图模式识别理论，即统计模式识别和人工智能模式识别。其中人工神经网络（Artificial Neural Network，ANN）作为一种人工智能技术被广泛应用于控制图模式识别研究。1989年，Pugh[1]首次提出将神经网络应用于过程控制中，并证明所提方法比传统休哈特控制图的性能更优越。HB Hwang[2]对BP神经网络（Back-propagation Network，BPN）应用于随机过程控制做出了研究，也取得了良好的效果。分析ANN在控制图模式识别的研究成果概率神经网络（probabilistic neural network, PNN）在控制图模式识别中的运用较少。pecht D.F.[3]在1990年提出的PNN网络是一种4层前馈神经网络，与传统BP神经网络相比，概率神经网络的训练时间更短。然而PNN网络的自适应学习能力以及较强的容错能力主要取决于平滑因子。对优化PNN网络，很多学者也做出了相关的研究成果；K.Z.Mao等人[4]提出通过遗传算法选择合适的PNN的平滑因子，通过简化PNN的网络拓扑结构获得更高的分类精确率。

针对传统PNN网络应用于控制图模式识别中的不足，本文选择粒子群算法（Particle swarm optimization, PSO）对PNN的平滑因子spread参数进行优化，将优化的PNN网络对自相关过程的6种模式进行识别，以获得更高的控制图模式识别精度为研究目标，并通过模拟实验进行了验证。

1 控制图模式的划分及自相关过程

按照GB/T4091-2001对控制图模式判断的准则，异常状态分为8种，本文主要对其中的6种模式进行研究分别为正常模式（NOR）、向上阶跃模式（US）、向下阶跃模式（DS）、上升趋势模式（IT）、下降趋势模式（DT）和周期模式（CYC），如图1所示。

生产过程中的数据很容易产生自相关性，违背了控制图以数据相互独立的理论前提。因此在自相关过程中使用控制图会产生大量的虚发报警或漏发报警。Cook等[5]研究了BPN在监测自相关过程方差能得到较好识别率；孙静[6]在残差控制图的基础上进一步解释了自相关过程受控状态的含义。

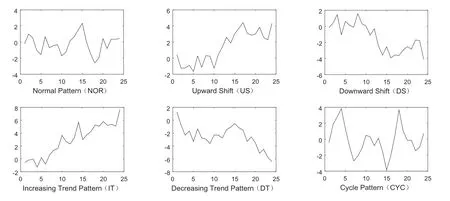
图1 6种基本控制图模式

在自相关过程的研究中，通常利用时间序列来描述自相关过程的动态规律性。其中，一阶自回归模型AR(1)拟合的自相关过程在实际生产中最为常见，研究也最多。AR(1)过程可描述如下：

2 概率神经网络模型

PNN模型基于Bayes分类规则与Parzen窗概率密度估计方法的神经网络模型。PNN模型由4层组成分别为：输入层、隐含层、求和层和输出层。模型的基本结构如图2所示。

图2 PNN网络结构示意图

式中，Wi为输入层与输出层之间的连接权值，δ为平滑因子对分类有非常重要的作用，求和层计算得出故障模式的估计概率密度函数。输出层其作用是在每个模式的估计概率密度中选择最大后验概率密度的神经元作为整个模型的输出。

3 优化PNN网络的控制图模式识别

3.1 PSO优化算法

Kennedy和Eberhar在模拟鸟群觅食过程中发现了PSO算法的优化性能[7]。PSO算法的数学描述如下：

假设D维搜索空间中有n个粒子，第i个粒子的位置向量为xi=（xi1，xi2，…，xiD），第i个粒子的当前最优位置为pbesti=（pi1，pi2，…，piD），整个粒子群的当前最优位置为gbest=（g1，g2，…，gD），第i个粒子的位置变化率为vi=(vi1，vi2，…，viD)。粒子的速度和位置变化公式如下所示：

其中，和c1=c2=2为学习因子，Arand是0到1之间的随机数。

本文以测试精度作为目标函数，利用PSO算法优化平滑因子SPREAD参数。

算法步骤如下：

Step1：设定平滑因子的取值范围[0,10]，随机产生初始化种群。

制定完善合理的科研成果评价体系和科研成果转化政策，将科研成果转化纳入科研成果评价体系，作为创新性能力评价标准之一，并与绩效奖励、职称评聘、科研奖项的评比等挂钩，保证评价指标的多样化。可根据高校发展需求和实际发展状况制定若干权变量，明确奖励范围、奖励力度，提高对科研成果持有人的奖励力度，并保证实时激励，充分调动科研成果持有人的积极性和主动性。

Step2：根据粒子获得的平滑因子，构建PNN网络，计算识别精度即粒子的适应度值。

Step3：与当前局部最优pbest比较，更新局部最优值，使得目标函数最大。

Step4：每个粒子的局部最优值与当前全局最优值gbest比较，更新gbest，获得最大的目标函数值。

Step5：更新粒子的速度和位置。

Step6：迭代次数达到最大或者目标函数达到最优则终止循环，否则返回Step3。

Step7：返回的粒子群的全局最优值gbest为平滑因子的最优值。

3.2 随机产生自相关数据

本文通过AR(1)时间序列模型模拟产生自相关数据，其公式为：

Rt是具有一阶自回归AR(1)特性的时间序列数据，μ=80是受控状态的均值，φ是自相关系数，随机噪声et服从N（0，λσε）分布（0≤λ≤1噪声幅度参数）。Xt为t时刻的观测值，dt为异常波动，t时刻的异常波动为d(t)。窗口宽度为24，基于蒙特卡洛模拟产生训练样本集和测试样本集。

3.3 模式识别模型的基本框架

本文所构建的基于PSO优化概率神经网络的控制图模式识别模型框架如图3所示。

4 实验验证

为了验证构建的概率神经网络参数优化模型，进行了数值模拟实验，通过得出的实验结果确定出概率神经网络运用于自相关过程模式识别中的最优参数。

4.1 实验环境与实验数据

实验在台式计算机上进行软件环境为MATLAB 2015b。根据3.2节所述的训练样本集和测试样本集，如表1所示。

4.2 实验过程及结果

为了验证所构建的概率神经网络的参数优化模型的有效性，根据实验得出的结果进行客观分析。经过迭代得到的最优粒子编码及其适应度值如表2所示。

通过表2所示，经过30次迭代优化，PNN网络对6种基本控制图模式的平均识别精度在第30次迭代中达到最优，即平滑因子为2.34时，取得的最优适应度为0.9518。

由表3所示，每种模式的识别准确度都在90%以上，其中CYC模式的识别精度达到100%，US和DT模式的识别精度相对较低都为92.22%，经过计算得出的平均识别精度达到95.18%。

4.3 不同自相关水平的比较

优化的PNN网络用于自相关过程的控制图模式识别，为了分析不同自相关水平下优化的网络的模式识别性能，本文选择了相关系数为φ∈{0.9，0.7，0.5，0.3，0.1}55种情况进行比较，结果如表4所示。

表4所示的实验结果显示，自相关水平φ=0.5的识别精度最高，相关水平高于0.5或低于0.5识别精度都有降低；自相关水平对CYC模式的识别精度基本没有影响，都能达到100%；当φ=0.7时，NOR模式的识别精度达到最高100%；综上分析，数据的自相关水平对优化的PNN网络控制图模式识别性能会产生影响。

4.4 与BP神经网络对比识别精度

图3 构建模式识别模型框架

本文将基于PSO优化的概率神经网络控制图模式识别方法与BP神经网络（BPANN）进行比较研究。实验分别比较了不同自相关水平（φ∈{0.9，0.7，0.5，0.3，0.1}）下两种模型的过程异常模式识别准确率，如图4所示。

表1 训练与测试数据集

表2 最优粒子编号及其适应度值

表3 优化的PNN网络测试结果和准确率

表4 不同自相关水平的识别精度（%）比较

图4 不同自相关水平下优化的PNN网络与BP神经网络识别准确率对比

从图4中可见，正自相关系数无论相关程度的高低，优化的PNN神经网络比BP神经网络的识别准确率高，自相关水平越高BP神经网络的识别准确率越低，相比之下优化的PNN网络的识别准确率相对稳定。

5 结束语

本文针对概率神经网络中SPREAD参数对网络性能的影响，分别构建平滑因子不同的PNN网络，通过粒子群算法经过30次迭代优化最终确定出最优的平滑系数为2.34。优化后的PNN网络作用于自相关过程的控制图模式识别中，当自相关系数为0.5时，平均识别精度最高。与控制图识别领域常用的BP神经网络进行了比较，结果显示基于PSO优化的概率神经网络的控制图模式识别性能更强。

本文主要解决了PNN网络在自相关过程控制图模式识别应用中的平滑因子不确定问题，PSO算法简化了SPREAD参数通过经验进行调整的复杂过程。经过数据仿真实验，优化的PNN网络在自相关过程中的控制图模式识别中可以取得较强的分类效果。

[1]Pugh G A.Synthetic neural networks for process control[J].Computers and Industrial Engineering,1989,17(1-4):24-26.

[2]Hwarng H B.Detecting process mean shift in the presence of autocorrelation: a neural-network based monitoring scheme[J].International Journal of Production Research,2004,42:573-595.

[3]Specht.D.F. Probability Neural Networks[J].Neural Networks,1990,3:109-118.

[4]Mao K Z, Tan K C,Ser W. Probabilistic Neural-network Structure Determination for Pattern Classification[J].IEEE Transactions on Neural Networks,2000,11(4):1009-1016.

[5]Cook D. F., Zobel C. W., Nottingham Q. J.Utilization of neural networks for the recognition ofvariance shifts in correlated manufacturing process parameters[J].International Journal of Production Research,2001,39(17):3881-3887.

[6]孙静,自相关过程的统计控制状态[J].管理工程学报,2003,17(2):75-80.

[7]Kennedy, J.,Ebethart,R.C Particle swam optimization[A].Proceedings of IEEE international Conference on NeuraI Networks[C].1995,1942-1948.