基于改进复制动态演化博弈模型的最优防御策略选取

黄健明，张恒巍



基于改进复制动态演化博弈模型的最优防御策略选取

黄健明1,2，张恒巍1,2

（1.信息工程大学三院，河南 郑州 450001；2. 数学工程与先进计算国家重点实验室，河南 郑州 450001）

针对同一博弈群体之间存在策略依存性，通过引入激励系数，改进传统复制动态方程，完善复制动态速率计算方法，构建基于改进复制动态的网络攻防演化博弈模型。利用改进复制动态方程进行演化均衡求解，采用雅可比矩阵的局部稳定分析法对所求均衡点进行稳定性分析，得到不同条件下的最优防御策略。研究结果表明，同一群体的不同策略之间既存在促进作用，也存在抑制作用。通过实验仿真验证了所提模型和方法的准确性和有效性，为解决现实社会中的信息安全问题提供了新的理论支撑。

策略依赖性；激励系数；改进复制动态；复制动态速率；雅可比矩阵；最优防御策略

1 引言

“互联网+”时代[1]的到来，使互联网在给人类社会带来便利的同时，也带来了日益严峻的网络安全问题。由于网络规模日益扩大，网络攻击手段日益复杂化、智能化和多样化[2~4]，入侵检测、防火墙[5~7]等传统的静态防御措施已经无法满足当前网络安全的需要，如何确保网络空间安全成为一个亟待解决的问题。

网络攻防对抗过程具有目标对立性、关系非合作性以及策略依存性等特征，与博弈论的基本特征保持一致[8]，因此，将博弈论应用于网络信息安全已经成为该领域的研究热点。目前的研究成果大都基于传统博弈理论[9,10]，Lye等[11]基于博弈双方的目标对立性和策略依存性，构建了静态网络攻防博弈模型，用于网络安全行为分析，但网络攻防具有动态变化特性，静态博弈模型无法分析其动态变化过程。基于此，林旺群等[12]基于非合作、非零和动态博弈理论提出了完全信息动态博弈主动防御模型，对网络安全主动防御技术问题进行了研究，对网络攻防动态对抗过程进行了分析，但完全信息条件在实际中无法满足，从而降低了模型的现实意义。姜伟等[13]通过建立不完全信息随机博弈模型，对入侵意图、入侵目标以及策略的选取进行推理。张恒巍等[14]针对具有不完全信息的动态攻防过程，提出了基于攻防信号博弈模型的防御策略选取方法。这些方法均停留在单阶段博弈分析的基础上，而实际网络攻防属于一个多阶段博弈过程，从而降低了模型和方法的适用性。基于此，王长春等[15]将网络攻防对抗过程与Markov随机过程相结合，构建多阶段Markov网络攻防对抗博弈模型，用于网络行动策略选取分析。但上述研究均以行为者完全理性为前提。由于现实社会中人的有限理性约束，网络攻防行为不可能达到完全理性，因此，完全理性假设与实际情况不符，从而降低了模型和方法的准确性。

演化博弈[16]是传统博弈理论与生物进化理论相结合的产物，建立在博弈者有限理性的前提条件下，以群体为研究对象，不仅继承了传统博弈模型的对抗性、非合作性以及策略依存性等特点，还具有动态演化的特征，强调博弈过程的动态演化[17]，与网络攻防实际更加契合。部分学者已经开始将演化博弈理论应用于网络信息安全领域，但目前相关研究还处于起步阶段。孙薇等[18]将演化博弈理论应用于网络信息安全，采用复制动态对网络攻防对抗的动态演化过程进行了研究，但仅对2种策略进行分析，模型的扩展性和适用范围有限。朱建明等[19]基于非合作演化博弈理论，提出了攻防双方信息不对称情况下具有学习机制的攻防演化博弈模型，并采用系统动力学进行过程分析，但仅对模型动力学进行分析，对安全防御指导作用不强。黄健明等[20]构建了基于非合作演化博弈理论的攻防演化博弈模型，采用复制动态对博弈均衡进行了求解分析，用于网络安全防御策略选取，但未对博弈演化过程进行具体分析，降低了模型的可信性。以上演化博弈模型均采用复制动态的学习机制，其思想是选取某一特定策略频率的变化等于该策略的适应度与群体平均适应之间的差值。然而，复制动态并未考虑同一群体下策略间的相互依赖关系。在实际网络攻防过程中，不仅攻防双方策略之间存在依存性，防御策略之间以及攻击策略之间均存在一定的依赖关系。

本文通过引入激励系数，用于表示同一博弈群体中的策略依存关系，改进传统复制动态方程，提高计算复制动态速率的准确性。然后，以实际网络攻防为背景，基于非合作演化博弈理论，构建基于改进复制动态的网络攻防演化博弈模型并对其进行均衡求解。最后，采用雅可比矩阵的局部稳定分析法[21]对所求均衡点进行稳定性分析，得到了不同条件下的博弈演化趋势和最优防御策略，可以用于网络攻击行为分析和预测，并为网络信息安全防御决策提供一定指导。

2 改进复制动态攻防演化博弈模型构建

演化博弈源于生物进化的思想[22]，学习机制是演化博弈的核心[23]，其中以复制动态[24]应用最为广泛。复制动态采用策略学习复制的思想，决策者通过模仿、学习的方法调整自身策略，该机制克服了最优反应动态[25]学习机制无法适用于学习能力较弱个体的问题，但是，并未考虑同一群体下策略之间的相互作用。基于此，通过引入激励系数，构建基于改进复制动态的网络攻防演化博弈模型，用于网络攻击行为预测和安全防御策略选取。

2.1 攻防演化博弈模型

图1 基本网络攻防博弈树

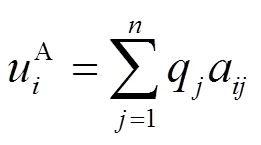
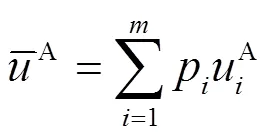
2.2 改进复制动态构造

由此可知

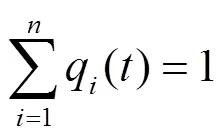
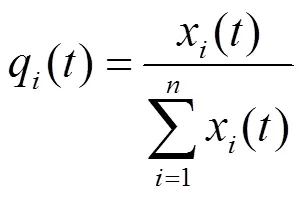
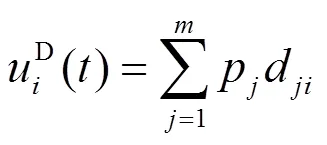
同理可知

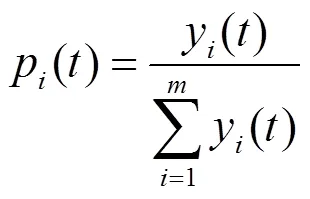
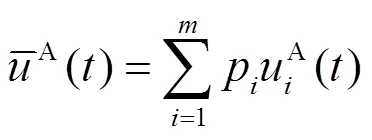
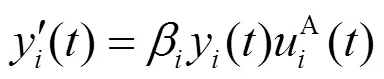
联立式(10)和式(16)，得到改进后的复制动态微分方程系统[28]为

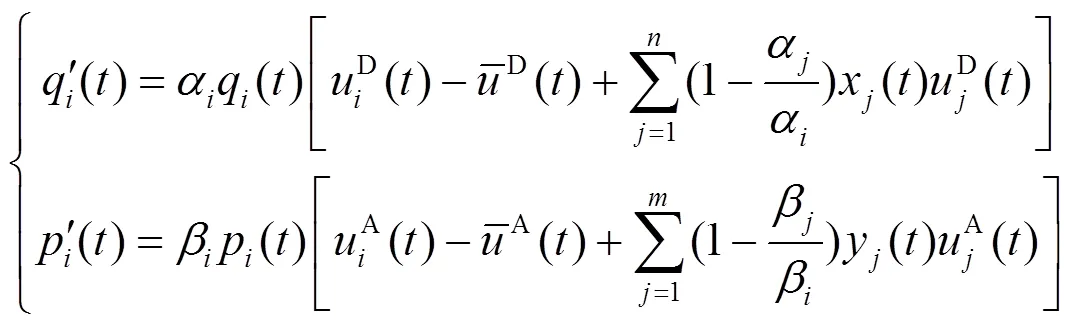
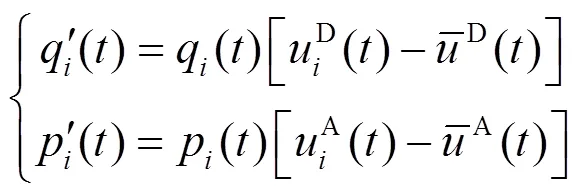
3 攻防演化稳定分析

基于上述提出的改进复制动态攻防演化博弈模型，针对攻防双方均具有2种可选策略的案例，对相应的改进复制动态方程进行均衡求解，并对不同均衡解进行稳定性分析，得到不同条件下的最优防御策略。

3.1 攻防演化博弈描述

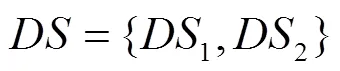
图2 网络攻防博弈树

3.2 攻防演化博弈求解

基于上述条件，结合第2.2节可得

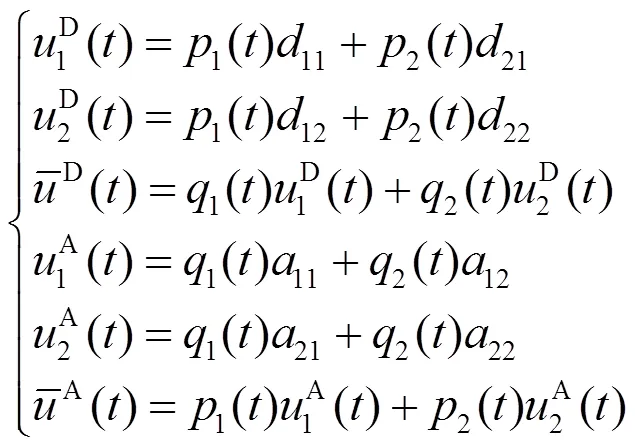
由

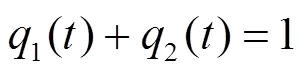
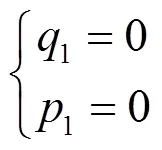
3.3 攻防演化动力学分析

针对上述建立的改进复制动态网络攻防演化博弈模型，采用系统动力学方法[30,31]对复制动态演化博弈系统进行分析，能够有效探索博弈系统内在的演化特性。

基于上述5个演化平衡点，采用雅可比矩阵的局部稳定分析法对所有演化平衡点进行稳定性分析。复制动态方程式(21)的雅可比矩阵为

(23)

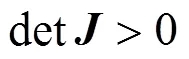
将上述4个点分别代入式(22)和式(23)，可以得到表1的结果。

表1 攻防博弈复制动态系统均衡点对应的雅可比行列式和迹计算式

针对雅可比行列式和迹的计算式，可以分以下4种情况进行分析讨论。

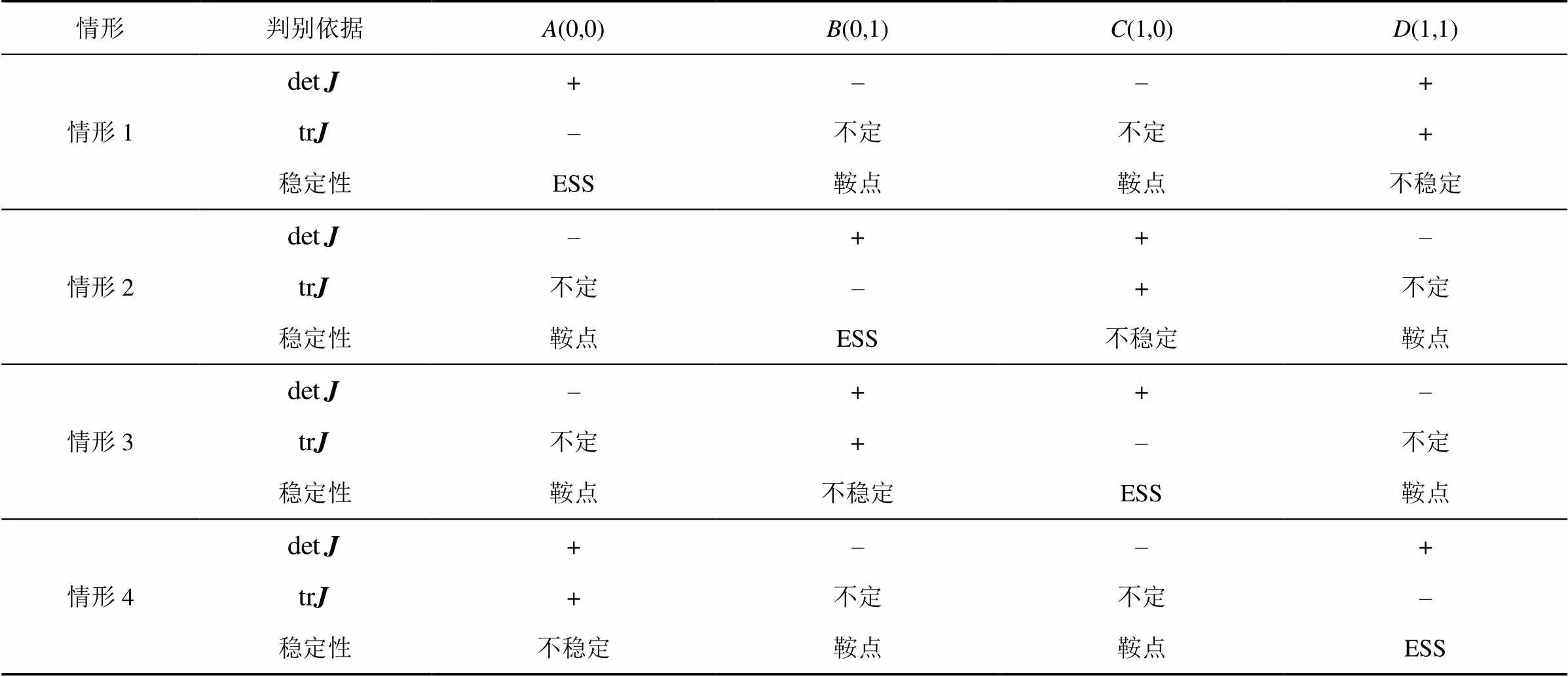
情形判别依据A(0,0)B(0,1)C(1,0)D(1,1) 情形1+––+ –不定不定+ 稳定性ESS鞍点鞍点不稳定 情形2–++– 不定–+不定 稳定性鞍点ESS不稳定鞍点 情形3–++– 不定+–不定 稳定性鞍点不稳定ESS鞍点 情形4+––+ +不定不定– 稳定性不稳定鞍点鞍点ESS

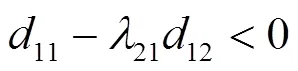
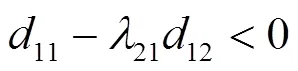
情形判别依据A(0,0)B(0,1)C(1,0)D(1,1) 情形1+––+ –不定不定+ 稳定性ESS鞍点鞍点不稳定 情形2+––– –不定+不定 稳定性ESS鞍点鞍点鞍点 情形3–++– 不定+–不定 稳定性鞍点不稳定ESS鞍点 情形4–+–+ 不定+不定– 稳定性鞍点不稳定鞍点ESS 情形5++–+ 不定–不定+ 稳定性不定ESS鞍点不稳定 情形6–++– 不定–+不定 稳定性鞍点ESS不稳定鞍点 情形7+–+– +不定–不定 稳定性不稳定鞍点ESS鞍点 情形8+––+ +不定不定– 稳定性不稳定鞍点鞍点ESS

情形判别依据A(0,0)B(0,1)C(1,0)D(1,1) 情形1+––+ –不定不定+ 稳定性ESS鞍点鞍点不稳定 情形2–++– 不定–+不定 稳定性鞍点ESS不稳定鞍点 情形3++–– –+不定不定 稳定性ESS不稳定鞍点鞍点 情形4––++ 不定不定+– 稳定性鞍点鞍点不稳定ESS 情形5––++ 不定不定–+ 稳定性鞍点鞍点ESS不稳定 情形6++–– +–不定不定 稳定性不稳定ESS鞍点鞍点 情形7–++– 不定+–不定 稳定性鞍点不稳定ESS鞍点 情形8+––+ +不定不定– 稳定性不稳定鞍点鞍点ESS

图4 当，时，攻防演化复制动态关系

同理，通过分析可以得出其他几种情形的演化关系，具体如图5~图11所示。

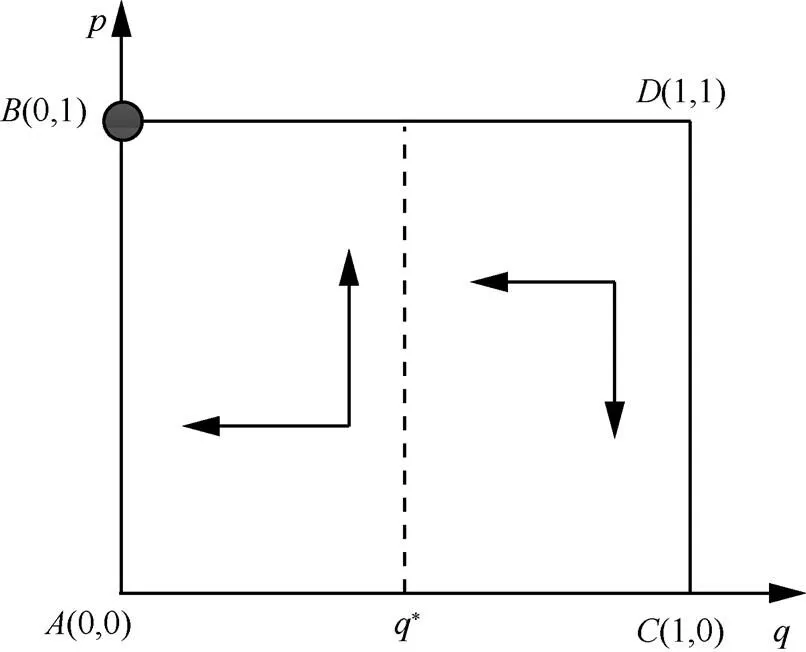
图5 当，时，不投资防御为防御方最优防御策略

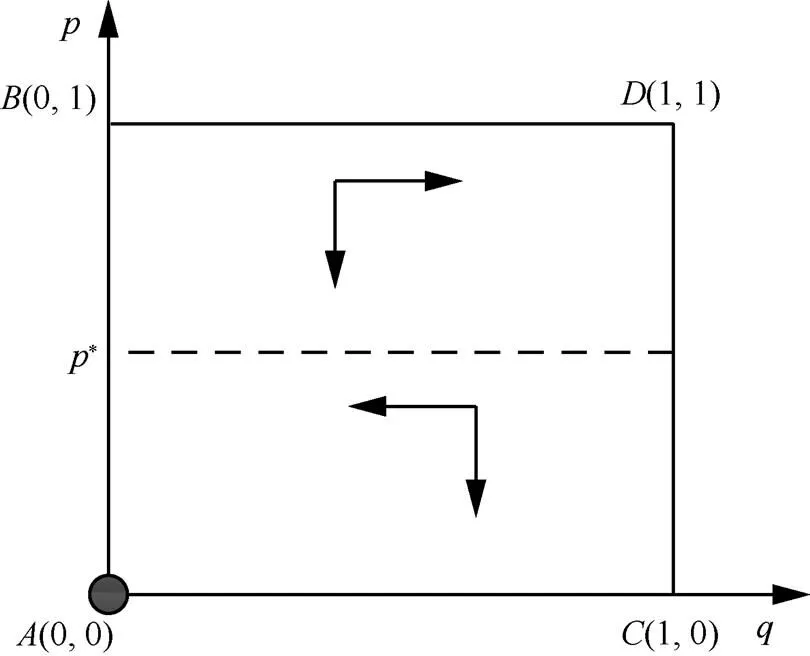
图6 当，时，不投资防御为防御方最优防御策略

图7 当，时，投资防御为防御方最优防御策略

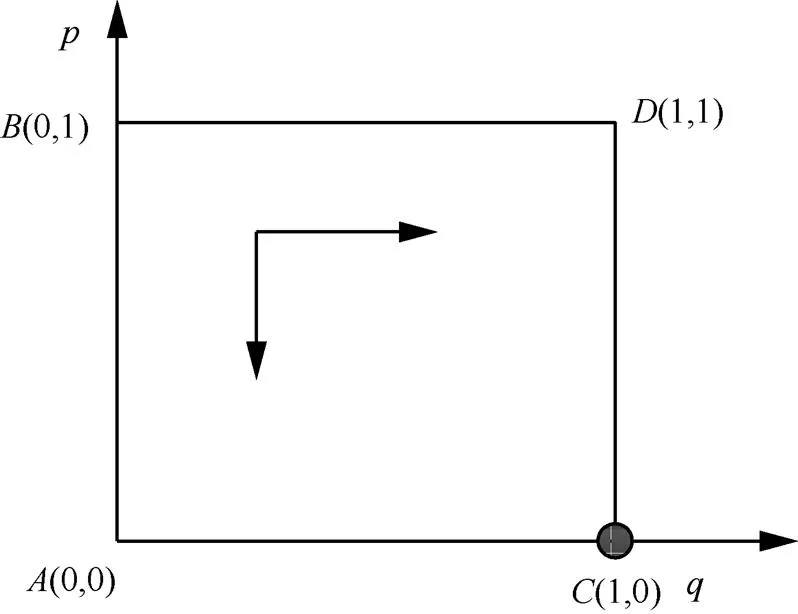
图8 当，时，不投资防御为防御方最优防御策略

图9 当，时，投资防御为防御方最优防御策略

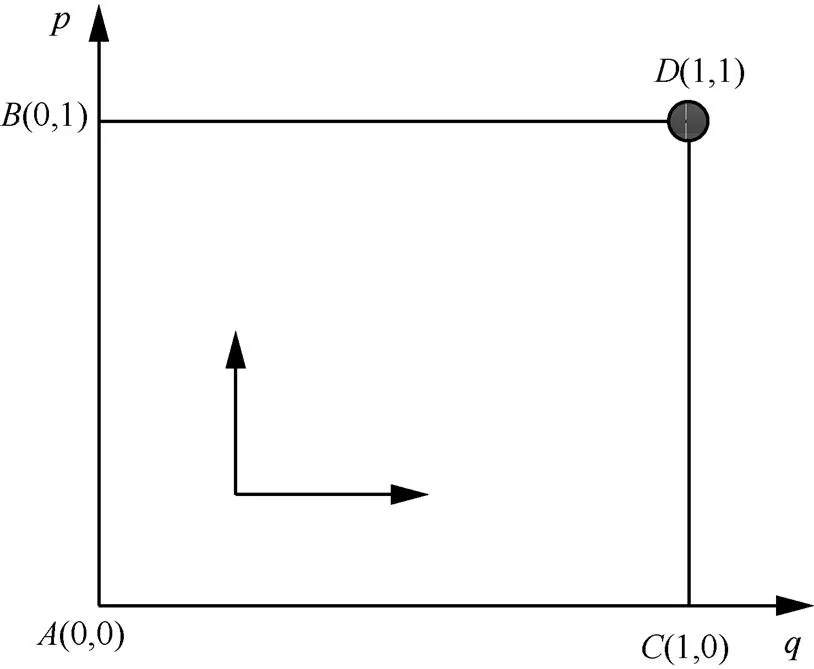
图10 当，时，投资防御为防御方最优防御策略

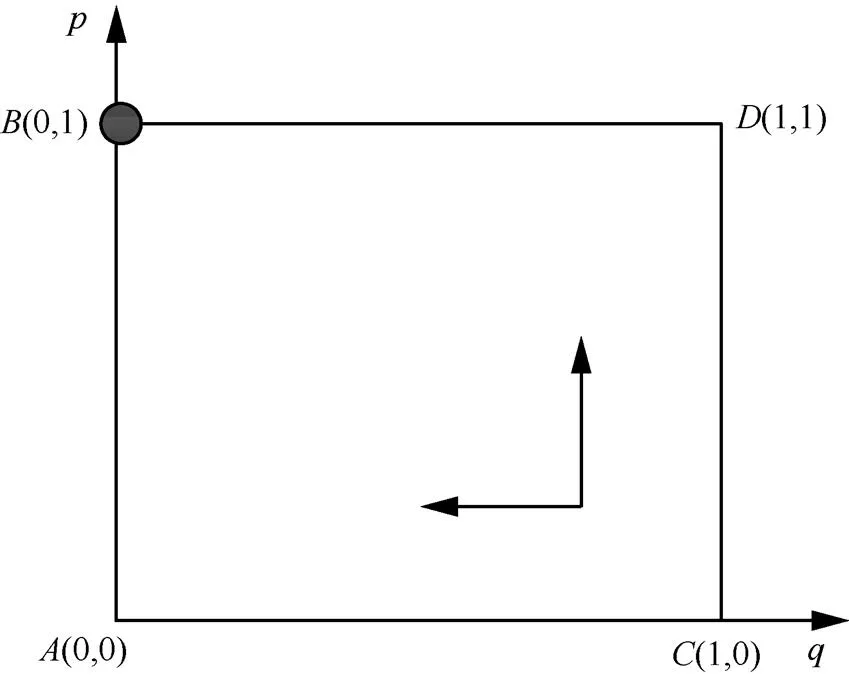
图11 当，时，不投资防御为防御方最优防御策略

3.4 模型和方法对比

将本文模型与方法同其他文献方法进行比较，可以得到比较结果如表5所示。网络攻防主要由人来控制，由于实现中人的有限理性限制，以决策者完全理性为前提的传统博弈理论与网络攻防实际不符。如文献[13,14]中的模型方法是以传统博弈理论为基础，完全理性条件降低了模型和方法的现实可行性。演化博弈建立在决策者有限理性的条件下，采用复制学习的思想更新个体策略，具有过程动态演化的特点，增强了模型和方法的现实基础。如文献[18,19]均是演化博弈模型，采用传统复制动态学习机制，摆脱了行为者完全理性的限制，但其模型和方法并未考虑同类（同一群体）策略之间的相互影响。在实际攻防过程中，不仅攻防双方策略之间存在依存性，防御策略之间以及攻击策略之间均存在一定的依赖关系，而这种同类策略之间的相互作用会对博弈演化过程中的复制动态速率产生较大影响，从而降低了模型和方法的准确性。

本文以决策者非完全理性的传统演化博弈理论为基础，综合考虑并定量描述同类策略之间的影响，通过引入激励系数，用于描述攻防双方同一群体策略之间的相互作用，改进传统复制动态方程，构建基于改进复制动态的网络攻防演化博弈模型，并对模型进行了分析与求解，提高了模型和方法的准确性。相比表5中其他文献的方法，本文方法对网络防御策略选取具有更强的针对性，采用该方法选取的最优防御策略更准确，对网络防御具有更好的指导意义。

表5 模型与方法比较结果

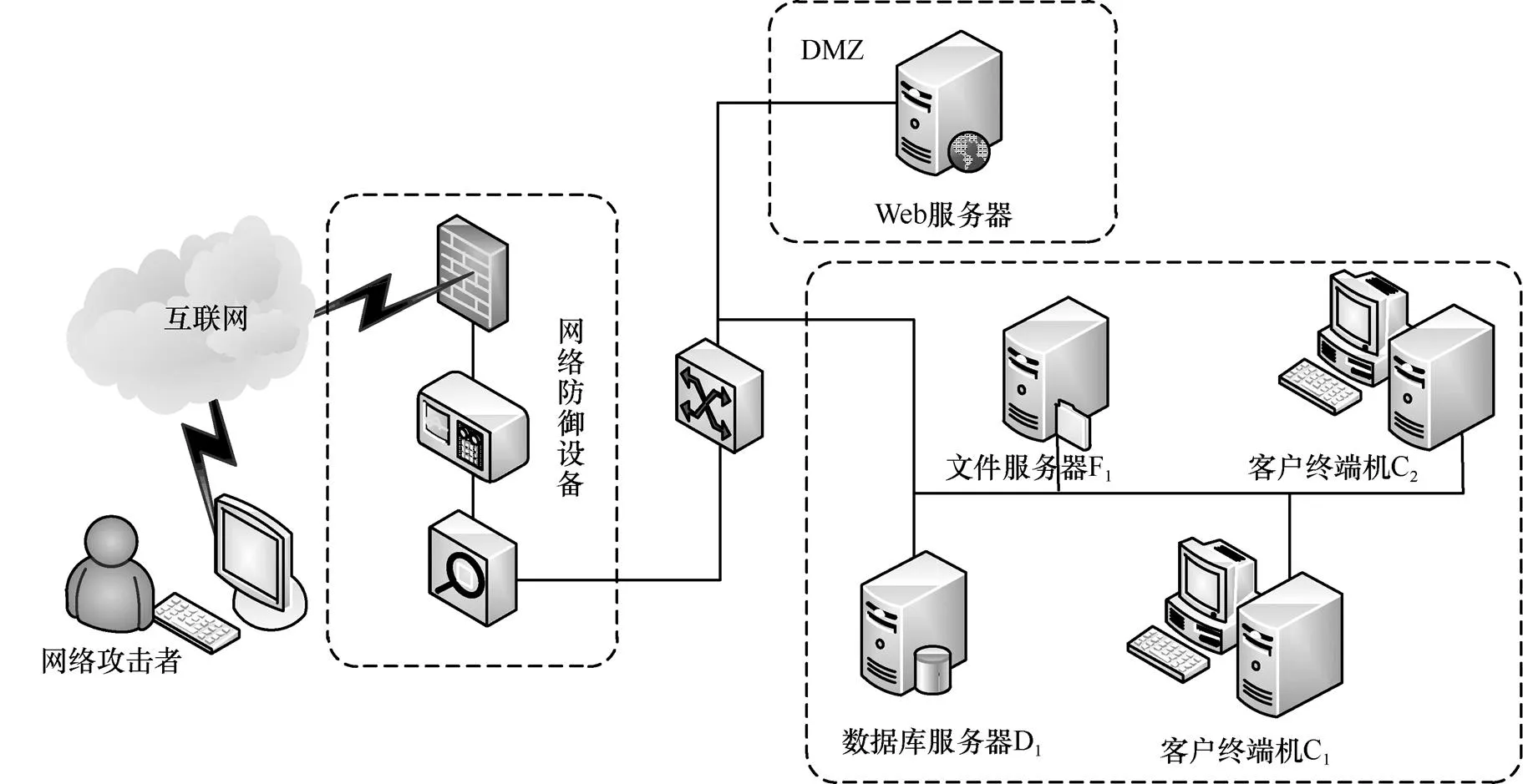
图12 网络信息系统的拓扑环境

4 实验仿真与分析

4.1 实验环境描述

基于本文提出的基于改进复制动态网络攻防演化博弈模型，通过部署一个简单的网络信息系统进行仿真实验，用于验证本文模型和方法的有效性。该网络信息系统的拓扑环境如图12所示，主要由网络防御设备、Web服务器、文件服务器、数据库服务器和客户终端机组成。通过防火墙将网络分为网络攻击者所在的外网区、DMZ隔离区和内网安全区3部分。在DMZ区域的Web服务器为Apache服务器；内网中的数据库服务器为Apache服务器提供数据库服务；客户终端机可以运行邮件、FTP和SSH程序。采用的访问控制规则是：非本网络的主机只能访问Web服务器，系统内Web服务器、应用服务器可以对数据库服务器进行访问。

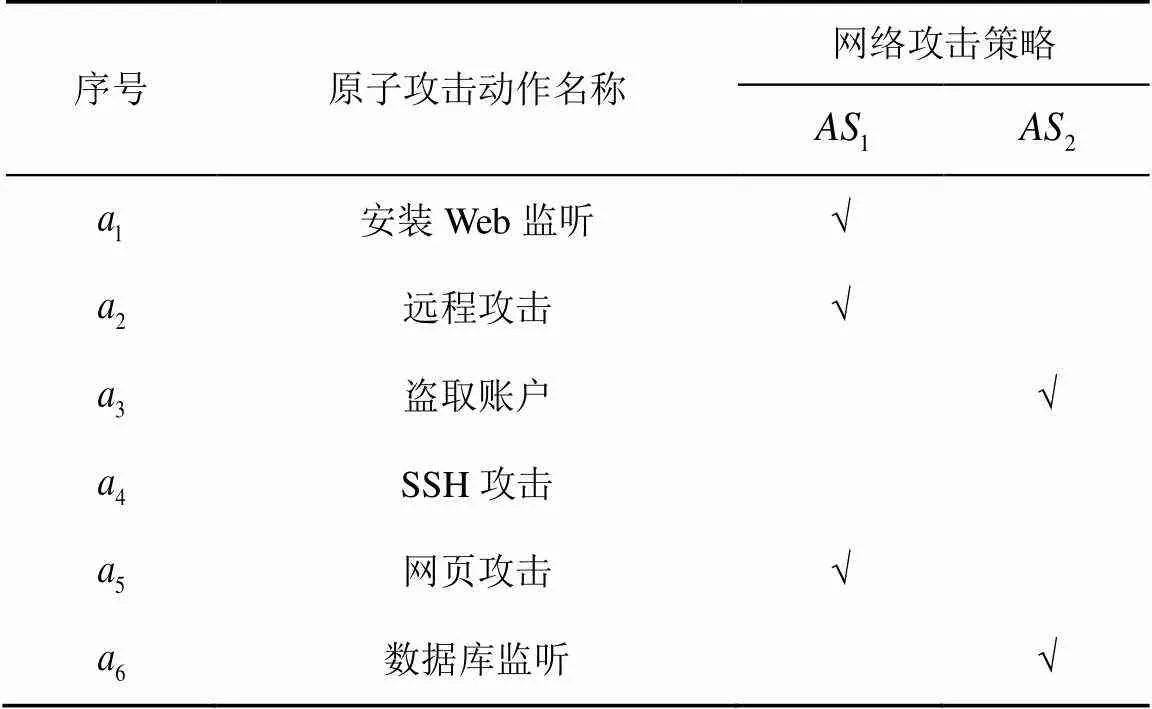
表6 原子攻击策略描述

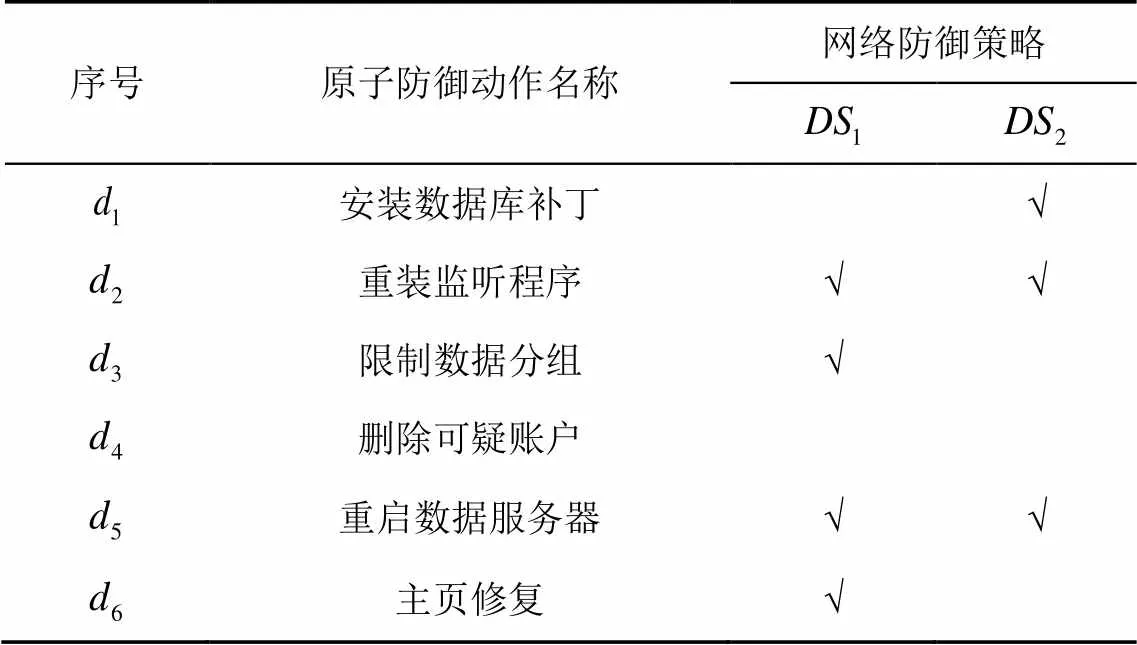
表7 原子防御策略描述

4.2 应用验证与分析

针对本文提出的改进复制动态攻防演化博弈模型，通过对激励系数设置不同取值，验证同一群体中不同策略之间的依赖关系对博弈演化过程的影响，突出改进复制动态演化博弈模型的优越性。其中，激励系数越大，表示策略之间的影响度越大；否则，表示策略之间的影响度越小。

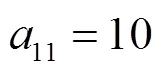
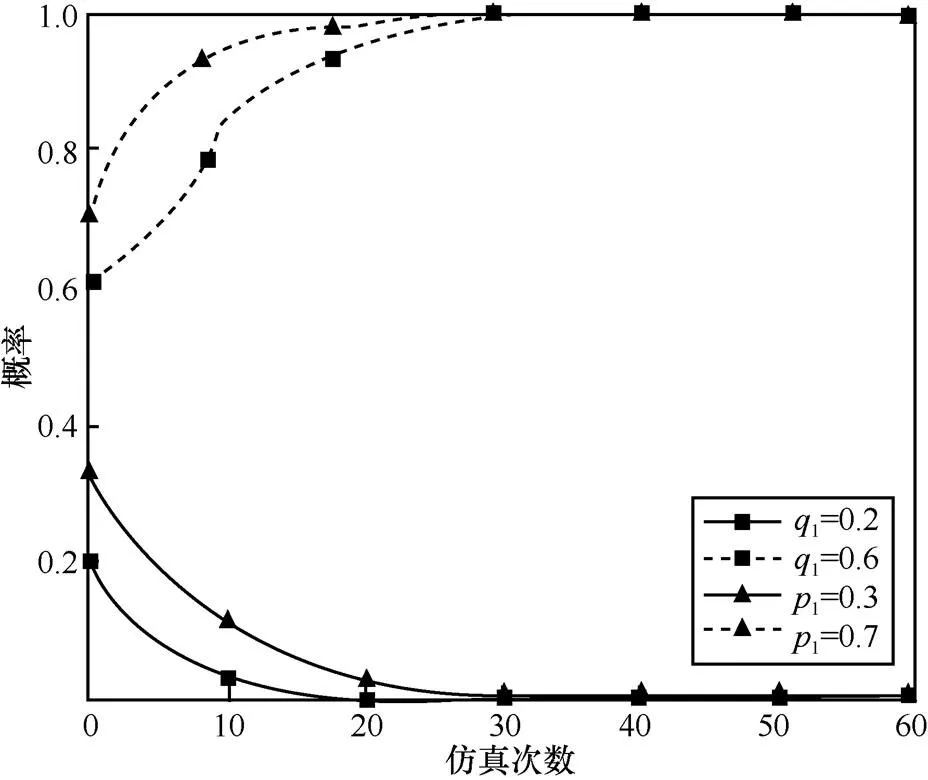
图13 当，时，不同初始状态下的攻防演化趋势

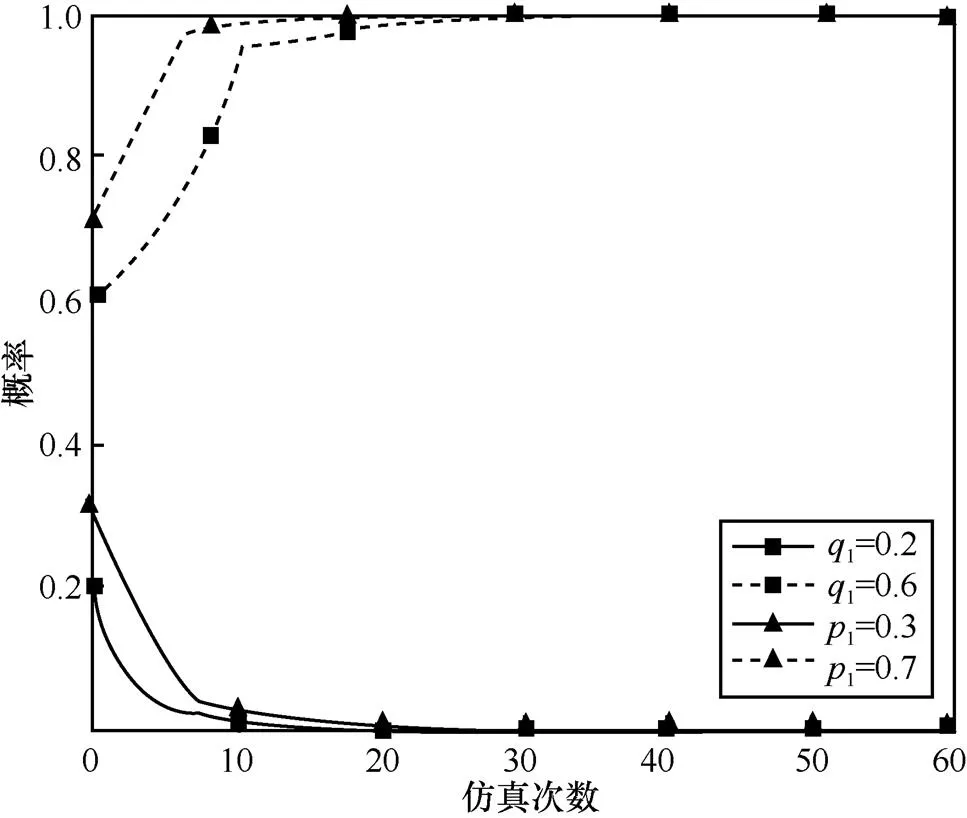
图14 当，时，不同初始状态的攻防演化趋势

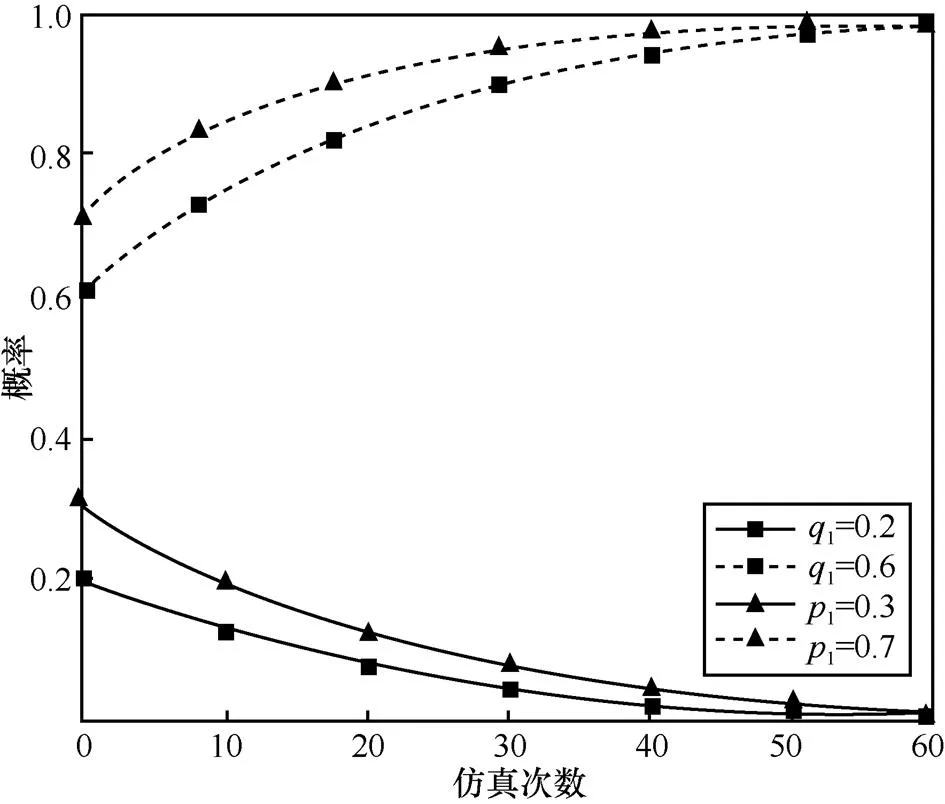
图15 当，时，不同初始状态的攻防演化趋势

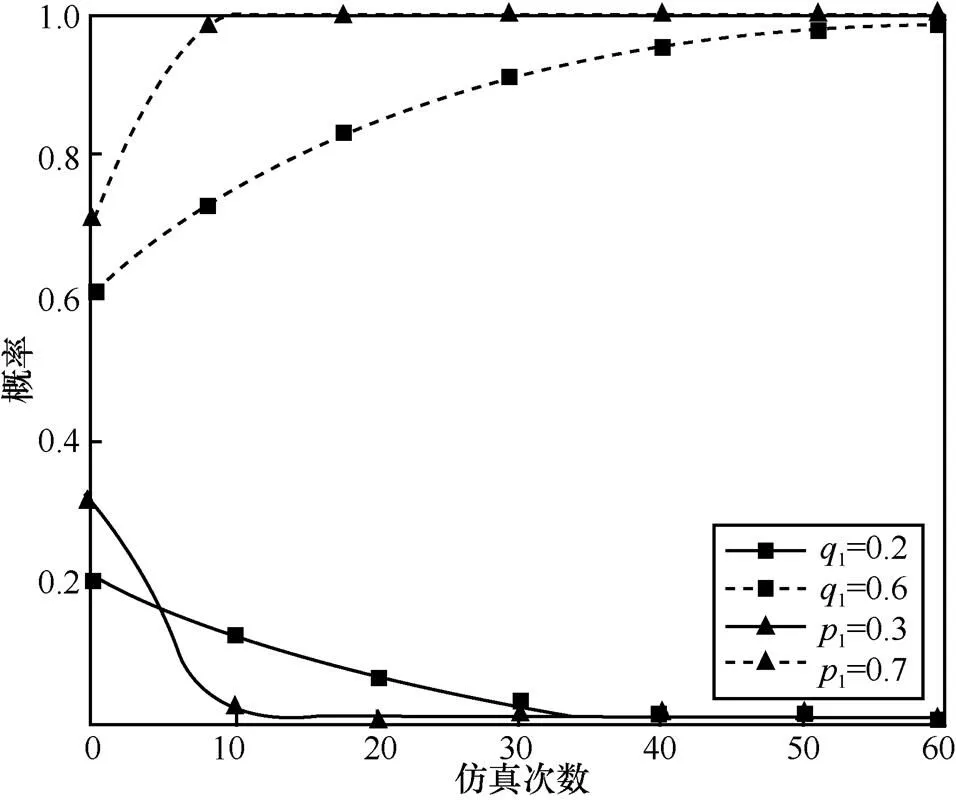
图16 当，时，不同初始状态的攻防演化趋势

由以上仿真结果可知，在给定各博弈参数取值的条件下，博弈系统在经过多次演化后，最终将收敛于某个稳定状态，得到相应的最优防御策略。通过观察对比发现，复制动态中激励系数的不同取值，对博弈系统演化的收敛速度具有不同的影响。由此可知，同一群体中的策略之间既存在促进作用，也存在抑制作用，实验仿真结果与本文所提模型中的理论分析保持一致，说明本文对传统复制动态方程的改进提高了模型和方法的准确性，可以用于指导网络安全防御决策。

5 结束语

本文针对同一群体中存在策略依存关系的问题，通过改进复制动态方程对网络攻防博弈过程中最优防御策略选取问题进行了研究。主要工作如下。

1) 从网络攻防实际出发，基于非合作演化博弈理论，通过引入激励系数，改进传统复制动态方程，构建基于改进复制动态的网络攻防演化博弈模型。

2) 利用改进复制动态方程进行均衡求解，采用雅可比矩阵的局部稳定分析法对所求均衡点进行稳定性分析，得到了不同条件下的最优防御策略。

3) 在给定各博弈参数取值的条件下，通过数值仿真，验证了激励系数在攻防博弈系统中对策略选取的激励作用。

研究结果表明，同一群体之间的策略存在相互依赖性，对博弈演化的收敛速度具有重要影响，这种依赖关系既包含促进作用，又包含抑制作用。研究成果拓展了演化博弈理论，对于在有限理性条件的动态攻防中实施网络防御决策具有指导意义，能够为开展网络空间攻防对抗研究提供模型和方法支持。但也还存在一些不足，如攻防策略集的确定以及激励系数的量化，这将成为下一步研究的重点。

[1] ROY S, ELLIS C, SHIVA S, et al. A survey of game theory as applied to network security[C]//43rd Hawaii International Conference on System Sciences, 2010: 1-10.

[2] LIANG X, XIAO Y. Game theory for network security[J]. IEEE Communications Surveys & Tutorials, 2013, 15(1): 472-486.

[3] VIDUTO V, HUANG W, MAPLE C. Toward optimal multi-objective models of network security: survey[C]//2011 17th International Conference on Automation & Computing. 2011: 6-11.

[4] GORDON L, LOEB M, LUCYSHYN W, et al. 2016 CSI/FBI computer crime and security survey[C]// 2016 Computer Security Institute. 2016: 48-64.

[5] SERRA E, JAJODIA S, PUGLIESE A, et al. Pareto-optimal adversarial defense of enterprise systems[J]. ACM Transaction on Information & System Security, 2015, 17(3): 11.

[6] RICHARD L, JOSHUA W. Analysis and results of the DARPA off-line intrusion detection evaluation[C]//17th International Workshop on Recent Advances in Intrusion Detection. 2015:162-182.

[7] EISENSTADT E, MOSHAIOV A, AVIGAD G. The competing travelling salespersons problem under multi-criteria[C]//2016 14th International Conference on Parallel Problem Solving from Nature. 2016: 463-472.

[8] GORDON L, LOEB M. Budgeting process for information security expenditures[J]. Communications of the ACM, 2016, 51(8): 395-406.

[9] WHITE J, PARK J S, KAMHOUA C A, et al. Game theoretic attack analysis in online social network (OSN) services[C]//2016 International Conference on Social Networks Technology. 2016: 1012-1019.

[10] OCEVICIC H, NENADIC K, SOLIC K. Game theory: active defense model and method[J]. IEEE Information and Network Security, 2016, 51(8):395-406.

[11] LYE K W, WING J. Game strategies in network security[J]. International Journal of Information Security, 2005, 4(1/2): 71-86.

[12] 林旺群, 王慧, 刘家红. 基于非合作动态博弈的网络安全主动防御技术研究[J]. 计算机研究与发展, 2013, 48(2): 306-316.

LIN W Q, WANG H, LIU J H. Research on active defense technology in network security based on non-cooperative dynamic game theory[J]. Journal of Computer Research and Development, 2013, 48(2): 306-316.

[13] 姜伟, 方滨兴, 田志宏. 基于攻防随机博弈模型的防御策略选取研究[J]. 计算机研究与发展, 2013, 47(10): 1714-1723.

JIANG W, FANG B X, TIAN Z H. Research on defense strategies selection based on attack-defense stochastic game model[J]. Journal of Computer Research and Development, 2013, 47(10): 1714-1723.

[14] 张恒巍, 余定坤, 韩继红, 等. 基于攻防信号博弈模型的防御策略选取方法[J]. 通信学报, 2016, 37(5): 39-49.

ZHANG H W, YU D K, HAN J H, et al. Defense policies selection method based on attack-defense signaling game model[J]. Journal on Communications, 2016, 37(5): 39-49.

[15] 王长春, 程晓航, 朱永文, 等. 计算机网络对抗行动策略的Markov博弈模型[J]. 系统工程理论与实践, 2014, 34(9): 2402-2410.

WANG C C, CHENG X H, ZHU Y W, et al. A Markov game model of computer network operation[J]. Systems Engineering -Theory & Practice, 2014, 34(9):2402-2410.

[16] MARTIN A N. Breaking the symmetry between interaction and replacement in evolutionary dynamics on graphs[J]. Physical Review Letters, 2016 (23):24-33.

[17] LI P, DUAN H B. Robustness of cooperation on scale-free networks in the evolutionary prisoner’s dilemma game[J]. A Letters Journal Exploring the Frontiers of Physics, 2014 (105):12-19.

[18] 孙薇. 基于演化博弈论的信息安全攻防问题研究[J]. 情报科学, 2015 (9): 1408-1412.

SUN W. Research on attack and deference in information security based on evolutionary game[J]. Information Science, 2015 (9): 1408-1412.

[19] 朱建明, 宋彪, 黄启发. 基于系统动力学的网络安全攻防演化博弈模型[J]. 通信学报, 2014, 35(1): 54-61.

ZHU J M, SONG B, HUANG Q F. Evolution game model of offense-defense for network security based on system dynamics[J]. Journal on Communications, 2014, 35(1): 54-61.

[20] 黄健明, 张恒巍, 王晋东, 等. 基于攻防演化博弈模型的防御策略选取方法[J]. 通信学报, 2017, 38(1): 168-176.

HUANG J M, ZHANG H W, WANG J D, et al. Defense strategies selection based on attack-defense evolutionary game model[J]. Journal on Communications, 2017, 38(1): 168-176.

[21] SHEN S G, HUANG L J, FAN E, et al. Trust dynamics in WSN: an evolutionary game-theoretic approach[J]. Journal of Sensors, 2016, 32(4): 34-43.

[22] LIU F M, DING Y S. Dynamics analysis of evolutionary game-based trust computing for P2P networks[J]. Application Research of Computers, 2016, 33(8): 2460-2463.

[23] FUDENBERG D, LEVINE D. Learning in games[J]. European Economic Review, 1998, 42(3-5): 631-639.

[24] GILBOA I, MATSUI A. Social stability and equilibrium[J]. Econometrica, 1991, 59(3):859-867.

[25] DREW F, JEAN T. Game theory[M]. Boston: Massachusettes Institute of Technology Press, 2012.

[26] BERGER U, HOFBAUER J. Irrational behavior in the Brown-von Neumann-Nash dynamics[J]. Games and Economic Behavior, 2006, 56(1): 1-6.

[27] SMITH M J. Stability of a dynamic model of traffic assignment-An application of a method of Lyapunov[J]. Transportation Science, 1984, 18(3):245-252.

[28] GUO H, WANG X W, CHENG H, et al. A routing defense mechanism using evolutionary game theory for delay tolerant networks[J]. Applied Soft Computing, 2016(38):469-476.

[29] TAYLOR P D, JONKER L B. Evolutionary stable strategies and game dynamics[J]. Mathematical Biosciences, 1978, 40(1/2):145-156.

[30] LEE W K, FAN W, MILLER M, et al. Toward cost-sensitive modeling for intrusion detection and response[J]. Journal of Computer Security, 2002, 10(1-2): 5-22.

[31] BORKOVSKY R N, DORASZELSKI U, KRYUKOV Y. A user’ s guide to solving dynamic stochastic games using the homotopy method[J]. Operation Research, 2015, 58(4): 1116-1132.

Improving replicator dynamic evolutionary game model for selecting optimal defense strategies

HUANG Jianming1,2, ZHANG Hengwei1,2

1. The Third College, Information Engineering University, Zhengzhou 450001, China 2. State Key Laboratory of Mathematical Engineering and Advanced Computing, Zhengzhou 450001, China

In terms of the existence of strategy dependency in the same game group, network attack-defense evolutionary game model based on the improved replicator dynamics was constricted by introducing the intensity coefficient, which completed the method of calculating replicator dynamic rate. The improved replicator dynamic equation was adopted to solve the evolutionary equilibrium for the situation that both attack and defense have two optional strategies. The stability of the equilibrium points was analyzed by the local stability analysis method of Jacobian matrix, and the optimal defense strategies were obtained under different conditions. The results show that the strategy dependency between the players in the same group has a certain influence on the evolution of the game, both the incentive and the inhibition. Finally, the accuracy and validity of the model and method are verified by the experimental simulation, which provides a new theoretical support for solving the information security problems in the real.

strategy dependency, strength coefficient, improving replicator dynamic, replicator dynamic rate, Jacobian matrix, optimal defense strategy

TP390

A

10.11959/j.issn.1000-436x.2018010

黄健明（1992-），男，湖南张家界人，信息工程大学硕士生，主要研究方向为网络安全主动防御。

张恒巍（1978-），男，河南洛阳人，博士，信息工程大学副教授，主要研究方向为网络安全与攻防对抗、信息安全风险评估。

2017-05-31；

2017-10-12

张恒巍，zhw11qd@163.com

国家自然科学基金资助项目（No.61303074, No.61309013）；河南省科技计划基金资助项目（No.12210231003, No.13210231002）

: The National Natural Science Foundation of China (No.61303074, No.61309013), Henan Science and Technology Research Project (No.12210231003, No.13210231002)