粮堆磷化氢浓度衰减阶段数学模型及验证研究

郭 超 王殿轩 劳传忠 沙宽宽 温湛清

(广东省粮食科学研究所粮食储藏与害虫防治研究室1，广州 510310) (河南工业大学粮油食品学院2，郑州 450001) (粮食储藏与安全教育部工程研究中心3，郑州 450001) (广州市白云区粮食储备公司4，广州 510440) (珠海市三灶粮食收储公司5，珠海 519040) (粮食储运国家工程实验室6，广州/郑州 510310/450001)

磷化氢是当前世界范围内应用最普遍的熏蒸剂，广泛应用在粮食、烟草、干果、药材等储藏物的杀虫处理。在中国的储粮熏蒸主要应用则以磷化氢仓外发生器施药、磷化铝粮面潮解施药、磷化铝布袋潮解施药、磷化铝探管施药等方式下的环流或非环流熏蒸技术应用为主。同磷化氢熏蒸杀虫技术，因技术掌握程度、应用操作水平、仓房密闭条件等差异，而出现不同的杀虫效果。磷化氢熏蒸失败的事例时有所见，二次或多次熏蒸的情况仍有存在[1]。磷化氢熏蒸杀虫的关键主要取决于有效浓度和在有效浓度下的熏蒸时间，实现熏蒸成功必须确保这两个影响因素超过一定的阈值[2-3，7，9]。熏蒸时间一般为粮堆密闭时间，在实际熏蒸过程易于掌握，而熏蒸中采用和保持合理的磷化氢浓度至关重要[4-5]。分析掌握熏蒸过程中磷化氢的浓度变化规律，对科学使用磷化氢并有效杀灭害虫具有重要的现实意义。

熏蒸是在密闭环境中进行的，一般施药后熏蒸剂浓度变化的基本过程分3个阶段，即毒气发生阶段、毒气衰减阶段、毒气排放阶段[1]。国内外对这3个阶段磷化氢浓度的变化规律报道主要分为基于熏蒸剂对流扩散和吸附特性建立的粮堆内部分布模型，以及粮堆熏蒸剂平均浓度随时间的变化模型。关于熏蒸剂在粮堆内部分布模型的类似研究也有一些探讨，王远成等[6]建立和验证了熏蒸剂(磷化氢)的对流扩散和吸附模型，并采用计算流体动力学方法对圆筒仓内谷物熏蒸过程中磷化氢质量浓度进行了数值预测，分析了熏蒸过程中磷化氢的质量浓度分布规律；Isa等[7]采用计算流体动力学方法，对立筒仓强制环流熏蒸和粮面施药熏蒸中磷化氢的浓度分布进行预测分析，研究发现立筒仓泄漏的部位对环流熏蒸中熏蒸剂的分布影响很大。若泄漏部位在立筒仓的底部，表层的害虫将杀灭困难，底部泄漏部位不影响粮面施药后熏蒸剂的分布，但接近立筒仓底层的磷化氢浓度保持低。采用计算流体动力学方法建立的粮堆内部熏蒸剂分布模型在改进熏蒸工艺设计时有一定参考，由于在建模过程多采用微积分，熏蒸实践中难以推广应用。张立力等[8]利用Wolfram对大型立筒仓磷化氢外环流熏蒸过程浓度和时间的变化建立模型，其中熏蒸剂发生阶段符合二次函数模型，浓度衰减阶段和散气阶段均符合冥函数模型；Cryer等[9]分别报道了硫酰氟熏蒸过程中熏蒸剂浓度衰减阶段和散气阶段的动力学模型符合C/C0=exp(-kt)(C0，熏蒸剂初始浓度；C，t时的熏蒸剂浓度；k,单位时间内衰减速度常数)；中国储备粮管理总公司等[1]报道了在不补充熏蒸剂到密闭环境中，熏蒸的浓度和时间呈指数模型变化C=C0exp(-(t-t0)k)或lnC0-lnC=k(t-t0)(C0，t0时刻熏蒸剂浓度；C，t时的熏蒸剂浓度；k,单位时间内衰减速度常数)，其中熏蒸密闭期间熏蒸剂的浓度在初始阶段迅速降低，之后以半对数的关系减少。从已报到的研究来看，其中提到的模型种类较多，但一些模型中含有的熏蒸剂初始浓度难以界定，磷化氢初始浓度的精确度影响到模型准确性，由此导致此类模型指导实际工作偏离度较大。

作者研究了在不进行熏蒸剂补充的密闭环境条件下，粮堆内磷化氢浓度随时间的变化规律，建立了粮堆内磷化氢平均浓度和熏蒸时间的模型，并进行了实仓验证，以期为解决生产中抗性害虫防治提供指导。

1 材料与方法

1.1 实验仓房

建模实验仓房采用广州市白云区粮食储备公司九佛直属粮库04-1A01仓，模型验证仓房采用珠海市三灶粮食收储公司P1仓、P2仓、P3仓。实验仓房均为高大平房仓，其储粮熏蒸基本条件见表1所示。

1.2 实验方法

1.2.1 仓房气密性测定

参照GB/T 25229—2010 平房仓气密性要求。

1.2.2 磷化氢浓度测定

广州市白云区粮食储备公司九佛直属粮库04-1A01仓和珠海市三灶粮食收储公司P1仓、P2仓、P3仓均在粮堆表层四角及中央设置5个气体取样点，用橡胶管引至仓外磷化氢气体检测箱内。粮堆的磷化氢浓度为5个气体取样点的平均浓度。熏蒸过程中，九佛直属粮库04-1A01仓不实施补药，珠海市三灶粮食收储公司P1仓、P2仓、P3仓浓度低于200 mL/m3时立即补药。

1.2.3 数据处理

模型的拟合和参数计算均采用SPSS 17.0和Excel 2010分析，本研究的分析结果为Excel 2010计算的结果，其中参数计算采用最小二乘法。数据的相关性分析采用SPSS 17.0双变量相关性分析，相关系数r选取Pearson相关系数。

2 结果与分析

2.1 熏蒸过程中粮堆内磷化氢浓度随时间变化

九佛粮库04-1A01仓磷化氢浓度随时间的变化如图1所示。由图1可知，在仓内粮面投放43.5 kg磷化铝后，磷化氢浓度逐渐升高。经第2 天环流4 h和第8天环流2.5 h，仓内磷化氢浓度在第9 天达到最高值，为692.2 mL/m3。随着时间的延长，磷化氢浓度逐渐降低，第28天浓度降低为194 mL/m3，第45 天浓度降低至33.6 mL/m3。对磷化氢发生阶段和衰减阶段浓度C和熏蒸时间t拟合曲线，结果表明磷化氢发生阶段浓度C和熏蒸时间t遵循C=2.62t3-44.50t2+264.87t模型(R2=0.960 24)，衰减阶段遵循C=1 649.1e-0.080 89t模型(R2=0.977 8)。根据衰减阶段模型计算出的磷化氢浓度与实测值相关系数0.990 8，这表明预测值与实测值具有较高的相关性。

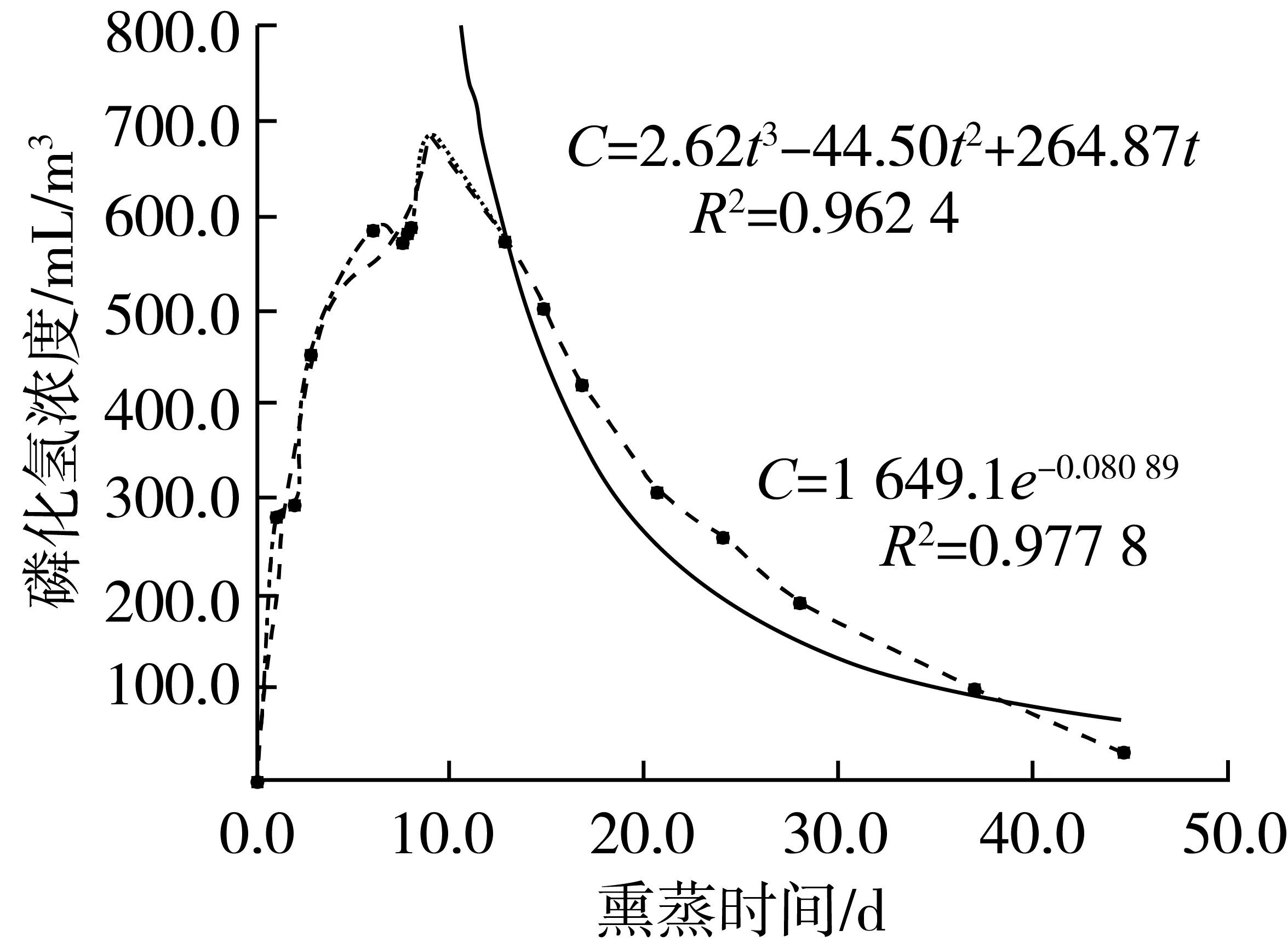
图1 九佛粮库04-1A01仓磷化氢浓度随时间的变化

2.2 磷化氢浓度-时间模型的建立及应用

基于九佛粮库04-1A01仓磷化氢发生阶段浓度C和熏蒸时间t遵循C=2.62t3-44.50t2+264.87t模型(R2=0.960 24)，衰减阶段遵循C=1 649.1e-0.080 89t模型(R2=0.977 8)，假定熏蒸过程中磷化氢浓度C和熏蒸时间t遵循上述模型，以磷化氢浓度最大值为分界点，建立磷化氢发生阶段和衰减阶段磷化氢浓度-时间模型，如下：

磷化氢发生阶段：C=αt3+βt2+γt(α>0，β<0,γ>0) Ⅰ

磷化氢衰减阶段：C=ae-bt(a>0；b>0) Ⅱ

其中C为磷化氢浓度，mL/m3；t为熏蒸时间,d；e为自然指数；α,β,γ,a,b均为常数。

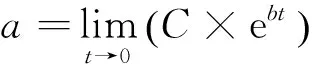
2.2.1 模型Ⅱ拟合所需的数据量分析

分别采用3个点至8个点拟合模型Ⅱ，采用最小二乘法计算获得a、b，并计算拟合度R2，如表2所示。从表2可知，采用3个点至8个点拟合模型Ⅱ，其数据与模型的拟合度均大于0.97，这表明采用3个或3个以上的数据即可得到拟合度高的模型Ⅱ。同时，采用不同数量的数据所得到的模型，预测磷化氢衰减阶段浓度的预测值与实测值相关性r均大于0.98，这表明采用不同数量的数据所得到的模型Ⅱ均可以较好的预测。如九佛粮库04-1A01仓磷化氢在28 d时浓度为194.6 mL/m3，而采用不同数量的数据所得到的模型Ⅱ分别预测浓度降至194 mL/m3的熏蒸天数如表2所示，结果表明采用3个数据拟合的模型预测的熏蒸天数误差最大，超过实际天数的5.6 d，但随着数据量的增多，预测的熏蒸天数由33.6 d逐渐减少并趋近于28 d，这表明随着数据量的增加，模型Ⅱ的预测的准确性不断提高。

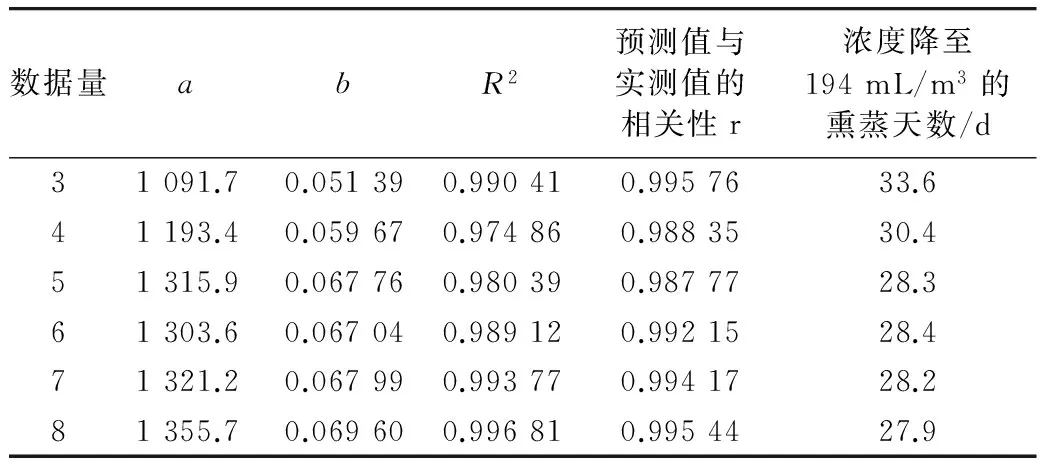
表2 不同数据量拟合的模型参数变化及预测值和实测值的相关性

2.2.2 计算磷化氢熏蒸最大浓度

根据磷化氢发生阶段模型I：C=αt3+βt2+γt(α>0,β<0,γ>0)和衰减阶段模型Ⅱ：C=a×e-b×t(a>0;b>0)，在t>0 d时模型分别为增函数和减函数。令αt3+βt2+γt=a×e-b×t，则两模型在t时刻相等，此刻磷化氢浓度为最大，即当t=9.6 d时，磷化氢浓度最大值Cmax=758.9 mL/m3[10]。磷化氢浓度半数衰减时间HLT为8.6 d。

2.2.3 计算磷化氢衰减阶段浓度和熏蒸时间

由C=ae-bt(即C=1 649.1e-0.080 89t)，计算到不同熏蒸时间对应的磷化氢浓度，如表3所示。由表3可知，实验期间九佛粮库04-1A01仓磷化氢浓度随时间的增加逐渐降低，且磷化氢浓度下降的幅度逐渐降低，其中14～21 d浓度降低了229.7 mL/m3，28～35 d浓度降低了74.1 mL/m3，42～49 d浓度降低了23.9 mL/m3，但每隔7 d浓度均以43.2%的比例降低。

表3 基于模型Ⅱ计算出的不同熏蒸时间对应的磷化氢浓度

令磷化氢浓度发生阶段模型Ⅰ：C=2.62t3-44.50t2+264.87t和衰减阶段模型Ⅱ：C=1 649.1e-0.080 89t浓度C分别为350、300、250、200、150、100 mL/m3，可计算到磷化氢浓度发生阶段和衰减阶段不同浓度下对应的熏蒸时间，如表4所示。

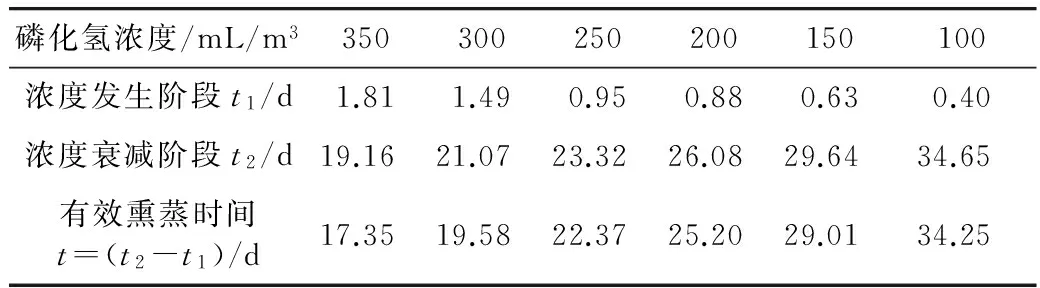
表4 基于模型Ⅰ和Ⅱ计算出的不同磷化氢浓度对应的有效熏蒸时间

2.3 模型Ⅱ在实仓熏蒸中的相关性与吻合度验证

2.3.1 P1仓实际熏蒸浓度变化与模型验证关系

P1仓压力从500 Pa降低至250 Pa，压力半衰期为105 s。熏蒸过程中P1仓共补药2次。由图2可知，磷化氢衰减阶段浓度和时间变化分3个阶段，均符合模型Ⅱ，且R2介于0.949 91～0.994 21，这表明模型的拟合度较高。由表5可知，P1仓磷化氢衰减阶段阶段Ⅰ、阶段Ⅱ、阶段Ⅲ浓度预测值与实测值的相关性r分别为0.995 6、0.988 5、0.970 4，这表明模型Ⅱ拟合效果好，磷化氢预测浓度接近实测值。

图2 三灶粮库P1仓磷化氢浓度随时间的变化

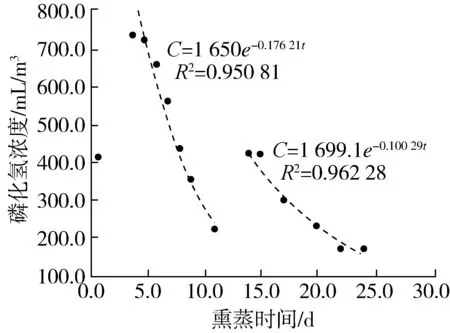
图3 三灶粮库P2仓磷化氢浓度随时间的变化 表5 三灶粮库P1仓磷化氢浓度预测值与实测值的相关性

模型实测值/mL/m3预测值/mL/m3r阶段Ⅰ:C=1139.3e-0.17001t582.0,517.0,443.5,304.8,253.3602.2,508.1,428.6,305.1,257.40.9956阶段Ⅱ:C=1895e-0.11637t468.6,427.8,403.8,305.0,263.0482.8,429.8,382.5,303.1,269.80.9885阶段Ⅲ:C=2444.5e-0.08712t442.6,424.5,412.0,380.3,363.0,297.5,201.0477.3,437.4,401.0,367.5,336.8,283.0,217.90.9704

表6 三灶粮库P2仓磷化氢浓度预测值与实测值的相关性

表7 三灶粮库P2仓阶段I磷化氢实测浓度对应的熏蒸时间

表8 三灶粮库P2仓阶段II磷化氢实测浓度对应的熏蒸时间

表9 三灶粮库P3仓磷化氢浓度预测值与实测值的相关性

2.3.2 P2仓实际熏蒸浓度变化与模型验证关系

P2仓压力从500 Pa降低至250 Pa，压力半衰期为96 s。熏蒸过程中P1仓共补药1次。由图3可知，磷化氢衰减阶段浓度和时间变化分两个阶段，均符合模型Ⅱ，且R2介于0.950 81～0.962 28，这表明模型的拟合度较高。由表6可知，P2仓磷化氢衰减阶段阶段Ⅰ、阶段Ⅱ浓度预测值与实测值的相关性r分别为0.958 3、0.984 9，这表明模型Ⅱ拟合效果好，磷化氢预测浓度接近实测值。此外，由表7、表8可知，P2仓磷化氢衰减阶段Ⅰ和阶段Ⅱ熏蒸时间预测值与实测值的相关性r分别为0.988 6、0.996 2，这表明模型II拟合效果好，磷化氢预测的熏蒸时间接近实测值。

2.3.3 P3仓实际熏蒸浓度变化与模型验证关系

P3仓压力从500 Pa降低至250 Pa，压力半衰期为69 s。熏蒸过程中P3仓共补药2次。由图4可知，磷化氢衰减阶段浓度和时间变化均符合模型Ⅱ，且R2介于0.924 54～0.999 38，这表明模型的拟合度较高。由表9可知，P3仓磷化氢衰减阶段阶段Ⅰ、阶段Ⅱ、阶段Ⅲ浓度预测值与实测值的相关性r分别为0.975 0、0.996 3，0.959 2，这表明模型Ⅱ拟合效果好，磷化氢预测浓度接近实测值。此外，由表10可知，P3仓不同磷化氢浓度下的预测熏蒸时间与图4吻合，其中第9.5 天、第18.2天时的磷化氢浓度为200 mL/m3。2015年12月8日P3仓开始施药熏蒸，根据熏蒸方案，此时应对粮堆补药。实际生产中，P3仓分别于第9 天(12月17日)和第19 天(12月27日)施药，这表明模型II拟合效果好，不同浓度下的磷化氢预测的熏蒸时间接近实测值。当磷化氢浓度下降至200 mL/m3时，阶段Ⅲ模型预测到的熏蒸时间为30 d，即下次补药应该在2016年1月7日。

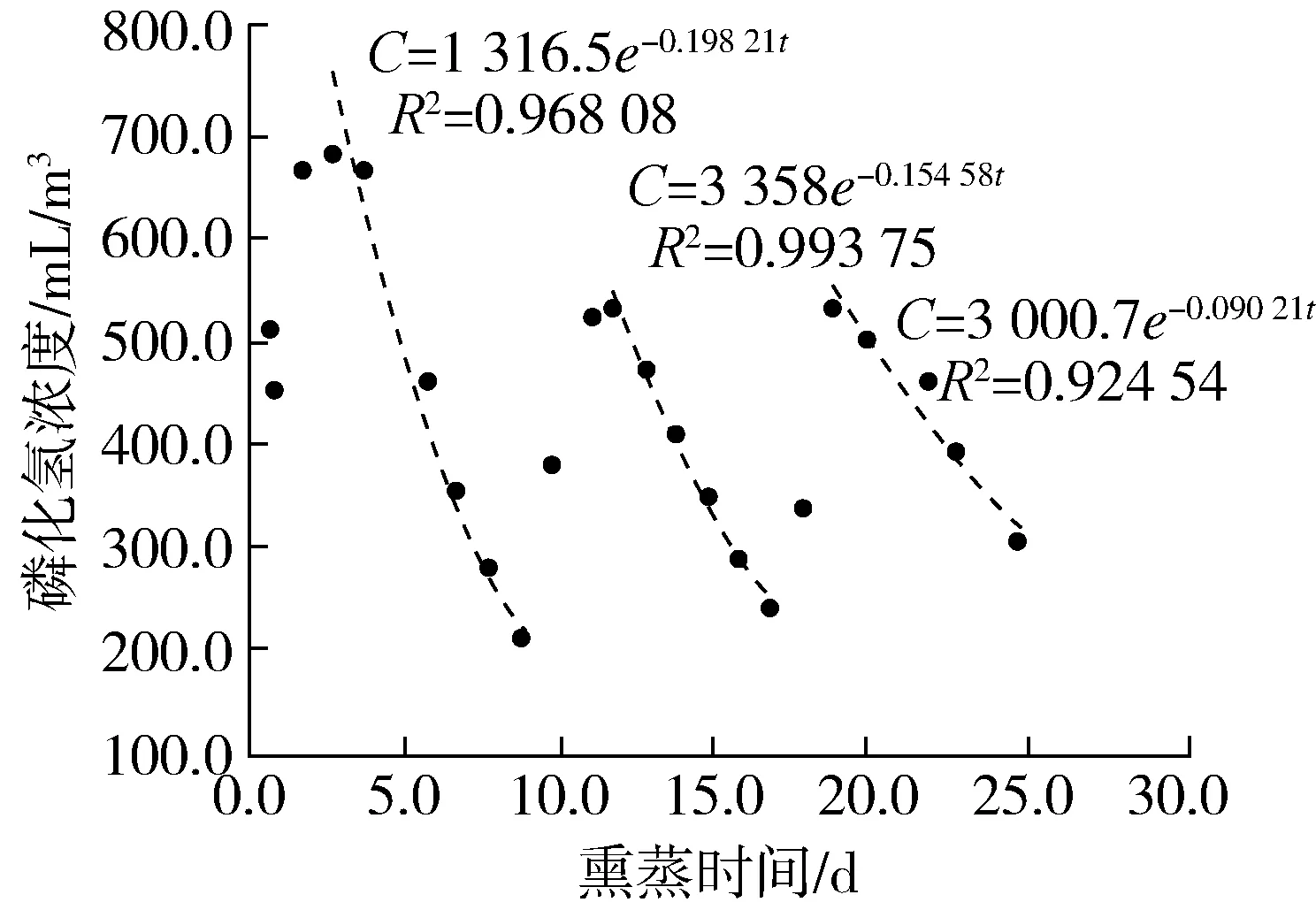
图4 三灶粮库P3仓磷化氢浓度随时间的变化 表10 三灶粮库P3仓不同磷化氢浓度下的预测熏蒸时间

磷化氢浓度/mL/m3熏蒸时间预测值/d阶段Ⅰ:C=1316.5e-0.19821t阶段Ⅱ:C=3358e-0.15458t阶段Ⅲ:C=3000.7e-0.09021t3506.714.623.83007.515.625.52508.416.827.52009.518.230.015011.020.133.210013.022.737.7

3 讨论

本实验以广州市白云区粮食储备公司九佛直属粮库04-1A01仓为建模实验仓，在不进行熏蒸剂补充的密闭环境条件下，分析了粮堆内磷化氢浓度随时间变化规律，构建了粮堆内磷化氢平均浓度和熏蒸时间的关系模型，其中磷化氢发生阶段模型Ⅰ：C=2.62t3-44.50t2+264.87t和衰减阶段模型Ⅱ：C=1 649.1e-0.080 89t。模型II在珠海市三灶粮食收储公司P1仓、P2仓、P3仓进行实仓验证。结果表明，衰减阶段磷化氢浓度随熏蒸时间的增加，磷化氢浓度呈指数下降趋势。衰减阶段模型II能够用于计算不同磷化氢浓度对应的熏蒸时间、不熏蒸时间对应的磷化氢浓度等指标，结合模型I还可计算磷化氢熏蒸最大浓度、最低熏蒸浓度下的有效熏蒸时间以及磷化氢浓度半数衰减时间HLT。此外，模型II还可用于预测粮堆的补药时间，指导粮食仓储行业实施磷化氢熏蒸作业。

九佛粮库04-1A01仓平均粮温为23.5 ℃，最低点粮温为22.3 ℃。根据GB/T 29890—2013 《粮油储藏技术规范表》E.1，当温度为20～25℃时不同虫种不同密闭时间的磷化氢熏蒸最低有效浓度设定要求，磷化氢保持最低有效浓度为350 mL/m3的密闭时间保持超过14 d以上，300 mL/m3时应超过21 d，250 mL/m3时应超过28 d。由表3可知，磷化氢保持最低有效浓度分别为350、300、250 mL/m3时，粮堆密闭的时间分别为17.35、19.58、22.37 d。虽磷化氢浓度为300、250 mL/m3时粮堆密闭时间均低于GB/T 29890—2013 《粮油储藏技术规范表》E.1规定，但磷化氢浓度为300 mL/m3时密闭时间超过14 d，从理论上讲，该粮堆中扁谷盗类(属)、蛾类、谷蠹、米象、书虱、螨类、赤拟谷盗、米扁虫及其他抗性虫种均应被完全杀灭。

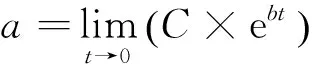
三灶粮库P1仓、P2仓、P3仓仓房压力半衰期分别为105、96、69 s，而三个仓阶段I单位时间内衰减速度常数b分别为0.170 01、0.176 21、0.198 21。从数值上看，随着压力半衰期的减少，衰减常数逐渐增大，即仓房气密性越差，仓内磷化氢衰减速度越快，这与实际情况相一致。同样，以三灶粮库P1仓阶段Ⅰ、阶段Ⅱ、阶段Ⅲ为例，单位时间内磷化氢衰减速度常数b分别为0.170 01、0.116 30、0.087 12。从数值上看，P1仓磷化氢衰减速度逐渐减慢。随着仓内磷化氢浓度的降低，仓内外浓度差逐渐减小，这可能导致磷化氢衰减速度逐渐减慢。在气密性较好的仓内熏蒸，对大多数熏蒸剂来说吸着将成为影响衰减速率常数的主要部分[12],因此，磷化氢衰减速度逐渐减慢还可能与粮堆吸附磷化氢有关。此外，九佛粮库04-1A01仓采用负压法测试仓房气密性，而三灶粮库P1仓、P2仓、P3仓采用正压法测试仓房气密性。高彬彬等[13]报道的北11仓和南11仓、周长金等[14]报道的安陆45仓和安陆49仓磷化氢熏蒸过程衰减阶段的浓度变化均符合本研究建立的模型。以上仓房无论使用负压法或正压法，熏蒸过程磷化氢衰减阶段浓度变化符合本研究提到的模型，实际上由于仓房压力半衰期测定主要在新建仓房验收时使用，在粮食保管过程中测定较少，而基于单位时间内衰减速度常数b可能与仓房压力半衰期、粮堆吸附磷化氢有关，进一步研究单位时间内衰减速度常数b，可能更好用于指导磷化氢熏蒸。

4 结论

粮堆内磷化氢浓度衰减阶段的浓度呈指数下降趋势。磷化氢浓度衰减阶段浓度和时间符合指数模型C=ae-bt(a>0；b>0)(其中C为磷化氢浓度,mL/m3；t为熏蒸时间,d；e为自然指数)。该模型可计算不同磷化氢浓度对应的熏蒸时间、不同熏蒸时间对应的磷化氢浓度、预测粮堆的补药时间等，用于指导粮食仓储行业磷化氢熏蒸作业。

致谢：感谢广州市白云区粮食储备公司九佛直属粮库戴惠良、刘柄和、滕俊涛等和珠海市三灶粮食收储公司伍灿洪、曹文杰、王山、黄海涛、肖小波、苏雄彬、陈锦锐等的工作。感谢广东省粮食科学研究所曾伶、卢木波、张少波、杨永强、冼庆、郑妙、张小松等对本工作的支持。

[1]中国储备粮管理总公司,河南工业大学.储粮磷化氢熏蒸技术区域优化[M].北京:中国农业科学技术出版社,2008 China National Grain Reserves Corporation, Henan University of Technology.Regional optimization of phosphate fumigation technology for sorage grain[M]. Beijing:China Agricultural Science and Technology,2008

[2]CHAYAPRASERT W, NUKHAM K, SUKCHAROEN A. Evaluation of the superposition method for predicting gas leakage rates during fumigations in empty model silos[J].Journal of Stored Products Research, 2015, 64, Part B: 13-20

[3]CHAYAPRASERT W, MAIER D E, SUBRAMANYAM B, et al. Gas leakage and distribution characteristics of methyl bromide and sulfuryl fluoride during fumigations in a pilot flour mill[J].Journal of Stored Products Research, 2012, 50: 1-7[4]王殿轩,卞科.储粮熏蒸剂的发展动态与前景[J].粮食储藏, 2004, 32(4): 3-7 WANG D X,BIAN K. Development trend of fumigant used in stored grain[J]. Grain Storage, 2004, 32(4): 3-7

[5]白旭光.储藏物害虫与防治[M].北京:科学出版社,2008 BAI X G. Stored product pest and control[M].Beijing: Science Press,2008

[6]王远成, Thorpe G R, 赵会义,等.储粮熏蒸过程中磷化氢浓度的分布模型及验证研究[J].中国粮油学报, 2015, 30(7): 81-84 WANG Y C, THORPE G R,ZHAO H Y,et al. The model and validation of phosphine fumigation in stored grains in silos[J]. Journal of the Chinese Cereals and Oils Association, 2015, 30(7): 81-84

[7]ISA Z M, FARRELL T W, FULFORD G R, et al.Mathematical modelling and numerical simulation of phosphine flow during grain fumigation in leaky cylindrical silos[J].Journal of Stored Products Research, 2016, 67: 28-40

[8]张立力,霍洪源,赵志永,等.立筒库磷化氢环流熏蒸模型的研究[J].粮食储藏,2000, 28(1): 27-32 ZHANG Z L,HUO H Y,ZHAO Z Y,et al.Study on silo recirculation fumigation model of phosphine in china[J]. Grain Storage, 2000, 28(1): 27-32

[9]CRYER SA,BARNEKOW DE.Estimating Outside Air Concentrations surrounding Fumigated Grain Mills[J]. Biosystems Engineering, 2006, 94(4): 557-572

[10]Wolfram Alpha LLC.Wolframalpha computational knowledge engine[EB/OL].[2016-03-02].http://www.wolframalpha.com/

[11]REED R C. Managing Stored Grain to Preserve Quality and Value[M].AACC International, 2005

[12]王殿轩,曹阳.磷化氢熏蒸杀虫技术[M].成都：成都科技大学出版社，1999 WANG D X,CAO Y. Phosphine fumigation technology[M].Chengdu: Chengdu University of Science and Technology Press,1999

[13]高彬彬,沈天翔,金宗铨,等.平房仓磷化氢膜下环流熏蒸技术的应用研究[J].粮食储藏, 2000,6:41-48 GAO B B,SHEN T X,JIN Z Q,et al.Trials of phosphine recirculation fumigation in grain bulk sealed surface with plastic sheet in horizontal bins[J]. Grain Storage, 2000,6:41-48

[14]周长金,马明君,李锡伟,等.不同气密性对环流熏蒸效果的影响[J].粮食储藏, 2003,5:21-23 ZHOU C J,MA M J,LI X W,et al. Effect of different gastightness on recirculation fumigation[J]. Grain Storage, 2003,5:21-23.