机械展开式再入飞行器柔性面材料力学性能仿真

董鑫 张红英 陈建平



机械展开式再入飞行器柔性面材料力学性能仿真

董鑫 张红英 陈建平

（南京航空航天大学飞行器先进设计技术国防重点学科实验室，南京 210016）

针对中国未来地球再入及深空探测的任务需求，开展了机械展开式再入飞行器的研究。文章基于机械展开式再入飞行器的结构特点，采用时空守恒元解元方法，建立三维非定常环境下机械展开式再入飞行器气动面的流固耦合数值模型。主要针对柔性面材料的弹性模量进行对比仿真计算，分析柔性面的变形及应力情况。通过对比分析得到：飞行器背部产生较明显的涡，起到抑制柔性面变形的作用；柔性面变材料的弹性模量的适用范围，当弹性模量为50GPa左右时满足使用要求；柔性面变形和应力的分布及大小，最大变形位置位于柔性面边缘，柔性面中部形成向内的凹陷，且其最大变量形略小于边缘变形量；文章讨论了柔性面厚度对变形量变的影响。文章结果为柔性面的气动特性及气动加热分析提供基础，也为柔性面的工程研制提供参考。

再入飞行器 机械展开式 流固耦合 柔性面材料 航天返回

0 引言

随着我国航天事业的发展，天地往返运输和深空探测任务将是今后的研究重点。针对未来地球再入及深空探测的任务需求，机械展开式再入（进入）飞行器应运而生。机械展开式再入（进入）飞行器具有体积小、质量轻、热流水平低、过载小、适用性好等优点，是国际上研究的重点[1]。机械展开式再入飞行器和传统类型的再入飞行器有较大区别，其柔性面结构较为特殊，需要考虑返回过程中结构变形和承载能力是否满足要求。此外，还需考虑柔性面变形对气动特性和气动加热特性等的影响，为进一步分析气动特性、气动热特性提供依据。柔性面结构的流固耦合问题是进行其他研究的基础，可以为柔性面材料的选择及工程研制提供一定的指导。

国内外一些研究学者已经对再入飞行器做了相关的研究，并取得了一定成果。文献[2]进行了机械展开式减速伞跨声速飞行时的数值研究，比较了DES方法和的RANS方法的不同影响，并将计算数据与“维京”号着陆器的实验数据对比验证；文献[3]发现展开式飞行器能适用于高热流、高压等极端情况，并指出了该方案的技术难点，尤其是柔性面变形的影响；文献[4]在研究火星计划所采用的可展开式飞行器时，利用NASTRAN软件模拟出特定攻角下气动面的压力及变形情况，但并未给出柔性面具体计算方法；文献[5]测试并分析了一种适用于自适应可展开进入和定位技术的3D碳纤维织物，可以满足热防护要求，但并未研究主要的承载层；文献[6-8]主要针对充气式再入飞行器的气动特性及相关技术进行了初步研究；文献[9]对半刚性机械展开式进行了技术述评，并指出流固耦合分析的重要性。

本文针对机械展开式再入飞行器的气动面进行流固耦合研究，通过分析得到柔性面材料的弹性模量的适用范围、柔性面变形和应力的分布及大小，以及柔性面厚度对变形的影响，为柔性面的气动特性及气动加热分析提供基础，也为柔性面的工程研制提供参考。

1 计算模型

机械展开式再入飞行器是一种新型的再入飞行器，其前端部气动面是一种可以从折叠状态到展开状态的结构。结构主要包括刚性防热头锥和柔性气动面：防热头锥由传统的刚性硬质防热材料制成，主要起热防护的作用，再入过程中具备可抛、分离的功能；柔性面与辐条连接，它是一种具备收纳和展开能力的新型柔性材料，随辐条展开后与刚性防热头锥形成球锥形气动外形，起到减速与防热作用。展开后的外形如图1（a）所示，主要由半顶角70°的刚性防热头锥、8块柔性气动面、8个连接辐条、撑杆、直径0.5m的货仓等部分组成，其中每块柔性气动面上边缘长约0.27m，下边缘长约0.86m，高约0.8m。

在流固耦合计算中考虑柔性壁面情况，流固耦合计算的主要目标是柔性面的变形量和应力分布。为节约计算时间简化模型，在建模过程保留防热头锥、柔性面、辐条和货仓部分，而忽略控制柔性面收放的一些机构结构以及连接装置等，这是因为其对气动面影响较小。将柔性面与头锥和肋条连接部位均设置为共节点来体现实际结构。

考虑到采用流固耦合在计算高超声速时耗费时间长，网格布置不能太密，因此在初步计算分析中划分网格如图1（b）所示，肋条较窄，以肋的宽度作为网格尺寸时计算量很大，故简化为梁单元。梁的形式以及材料属性也是影响结构流固耦合的因素，本文使用的梁是边长为3cm的矩形梁，材料为碳纤维双马来酰亚胺树脂复合材料。柔性面、防热头锥部分选用壳单元，分别如图中黄色和蓝色部分所示。NASA研究的机械展开式再入飞行器VITaL号，整个柔性面厚度为3.8mm，其中结构层约占厚度的2/5，因此，本文模型中设置柔性面厚度为2mm。

流场网格应适应该模型结构大小，流场前端面为进气口，后端面为出气口，周围为无反射壁面，中部气流与柔性面接触较多，网格划分较细与柔性面网格大小相当，越往外影响越小，网格可相对画粗，流场网格共计123万，如图2所示。流场入口方向设置为沿飞行器轴向方向，目前只考虑该来流方向。在飞行器轴线方向上，流场网格应与飞行器相匹配，所以该段网格较细，越往后网格可逐渐变粗，飞行器质心位置处于流场流向方向的三分之一处，能够较好的反应出激波及尾流的变化情况。

机械展开式再入飞行器的返回阶段是一个复杂的过程，选择返回过程中最大动压时的工况来模拟，可以有效的反映气动面所受的最严酷情况。因此，本文选择飞行器承受最大动压时刻的状态，最大动压为768Pa。

2 控制方法

2.1 CE/SE算法

目前柔性织物超声速流固耦合计算除了传统的CFD求解器加CSD求解器松散耦合方法外，主要采用基于LS-DYNA的ALE方法和时空守恒元解元方法（Space-time Conservation Element and Solution Element Method，CE/SE）[10-11]，它是求解双曲型守恒律方程的一种新型数值方法，可以求解一些复杂的流动，被NASA列为第二代CFD软件的主要算法之一[12]。其特点是使用泰勒展开构造格式，在捕捉激波间断时，仅处理数值导数项，提高了格式的求解速度并简化了格式的构造过程。在求解过程中，用类似紧致格式的方法计算各物理量的空间导数，使计算精度得到明显提高。该方法主要适于求解超声速流动并能较好地实现复杂激波的捕捉，且LS-DYNA求解器内部实现了CE/SE流场求解与FEM结构求解的界面耦合，使之能够对超声速流固耦合问题进行求解。目前CE/SE方法无法考虑织物透气性，无法考虑湍流、真实气体效应等，只能假设气体为完全气体、层流情形[13]。针对机械展开式再入飞行器的超声速流固耦合分析，采用该方法可以得到结构应力、变形等结果，并且较准确的分析流场情况，可以计算得到激波与结构的相互作用和干扰过程。

2.2 流固耦合算法

流固耦合问题按其耦合机理可分为两大类[14]：第一类是流固两域部分或全部重叠在一起；第二类是耦合作用仅发生在两相介质的交界面上，由流固耦合面上的平衡及协调关系来引入耦合方程。本文选择第二类，显式动力学积分方法求解充气过程的流固耦合问题，程序在每个时间步内首先需要分别计算流场网格和柔性面结构网格的节点力，之后将流体－结构交界面的节点力进行耦合[15]。当流体和柔性壁面网格一致，即流体节点与柔性壁面节点重合时，流固耦合界面处的数据传递通过对应节点完成；当流体和柔性壁面网格不匹配时，则需采用映射算子进行插值计算，将结构变形由柔性壁面网格传递给流体网格，流体荷载传递给柔性壁面网格。根据力平衡条件，流固耦合界面上沿法线方向流体应力与柔性壁面应力平衡。利用映射算子将流体节点应力插值到柔性壁面节点上，并利用柔性壁面边界插值函数积分得到柔性壁面节点力，作为有限元求解的自然边界条件。迭代弱耦合法中流场分析和结构分析具有独立性和完整性，利用LS-DYNA软件的优势，计算耗内存较少，适用于流固耦合的数值计算，对稳态分析处理较好，是目前用得最多的流固耦合气动弹性分析方法[16-17]。

3 结果分析

为了减小柔性面的变形，可以采用提高气动面的刚度或者增加辐条数目的方法，但是都会导致结构质量的增加。因此，在不改变飞行器气动面结构的基础上，本文采用不同材料参数分别进行气动面的流固耦合仿真实验。陈宇峰、陈务军等人研究表明，对于经纬向张力比接近1的薄膜结构，泊松比的变化对结构变形影响较小，而弹性模量变化对结构变形影响明显[18]。本文所采用的柔性面为单层薄膜结构，采用薄膜材料，经纬向张力比接近1，因此主要讨论材料的弹性模量对结构的影响，材料的密度和泊松比为定值，分别为1 180kg/m³和0.33。目前，碳纤维编织柔性材料的弹性模量可以达到200GPa，但考虑到柔性面在飞行器的其他工作状态下需要折叠收放，所以在满足使用要求的前提下材料的弹性模量应该尽可能小。根据工程实际情况确定四种弹性模量，分别为50MPa、500MPa、5GPa、50GPa。设定柔性面上特征曲线AB、CD、EF，曲线AB、EF各取15个特征点，曲线CD上取9个特征点，如图3所示。

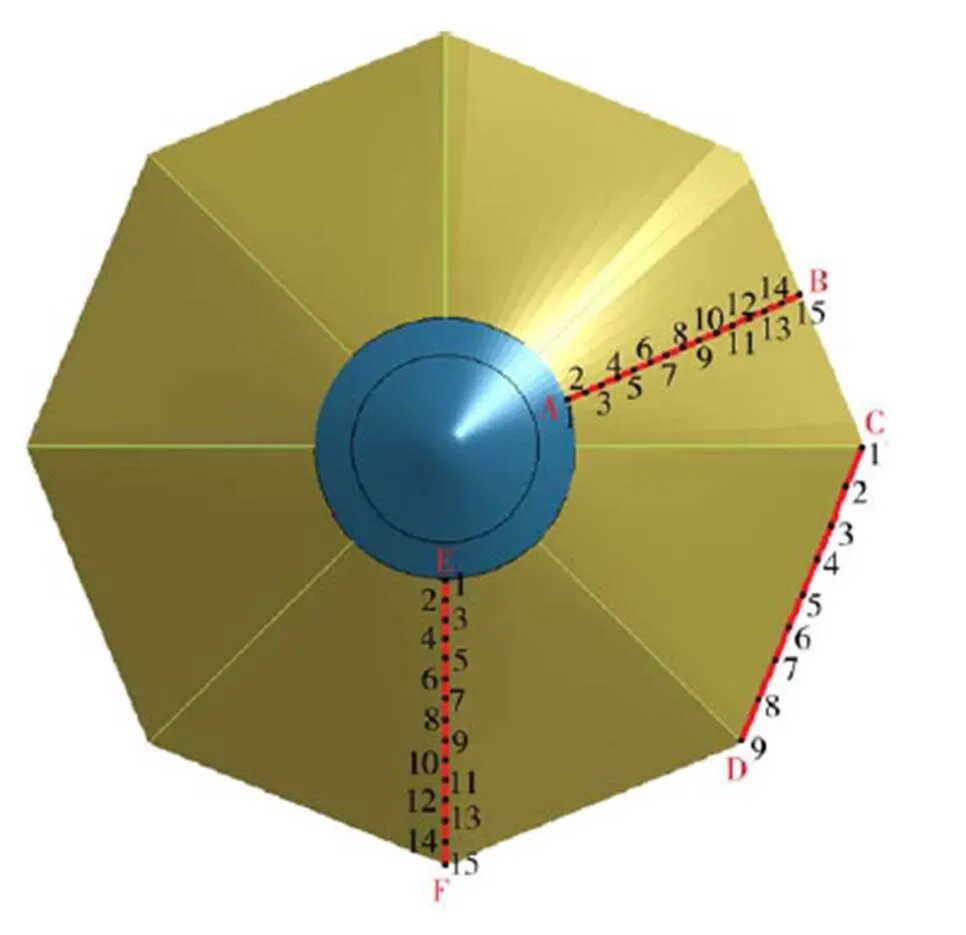
图3 特征曲线及特征点

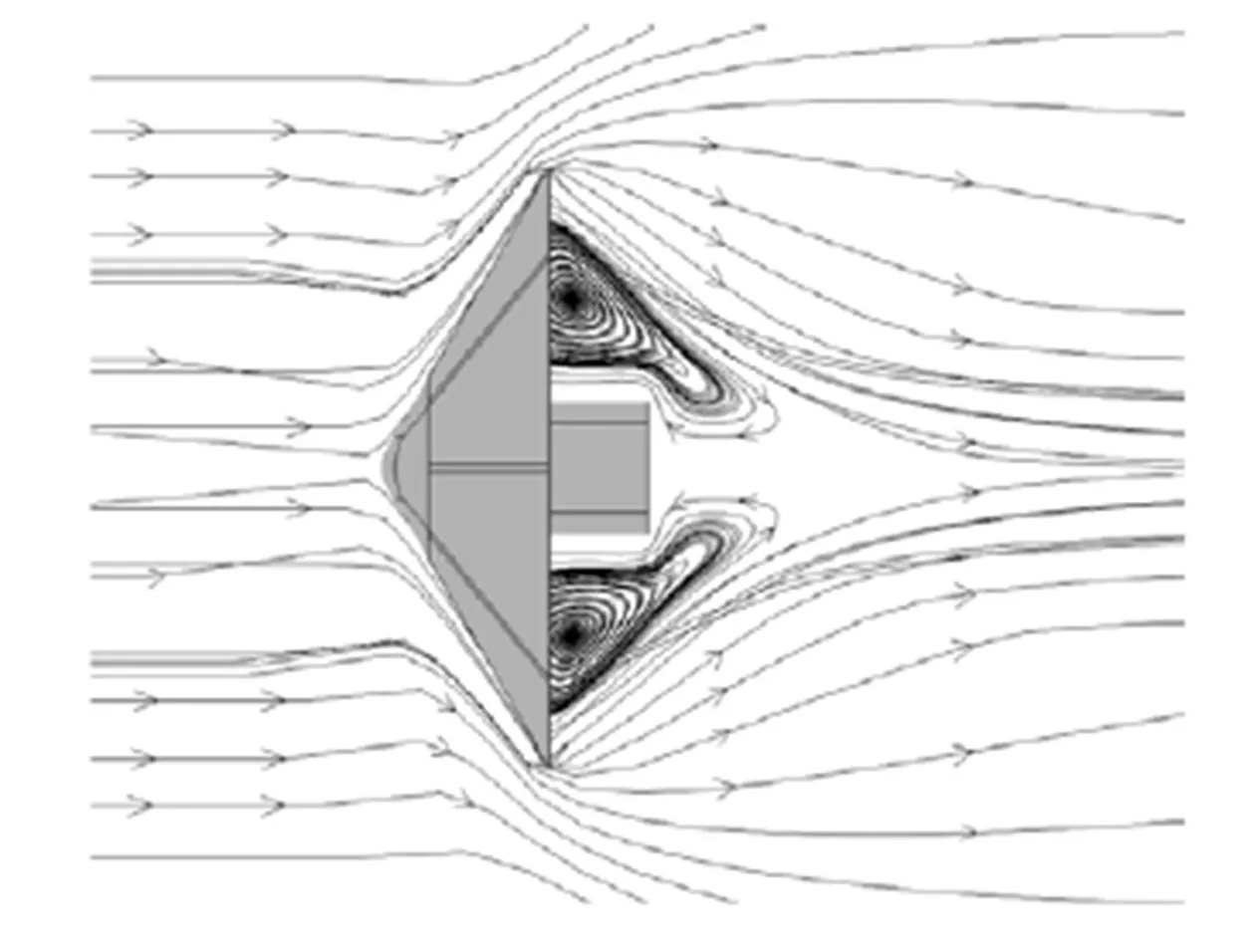
图4 流线图

3.1 流场分析

本文模型所处大气环境的密度为1.29kg/m³、压强为8.46Pa、温度为228.4K。图4给出了机械展开式再入飞行器气动面受载过程的流场计算结果。来流速度达到=10，来流流过柔性面边缘后，在柔性面的背部形成明显的尾涡，流线方向如图4中箭头所示。来流和尾涡共同作用在柔性面上，柔性面背后的涡对抑制柔性面变形起到一定作用。

3.2 气动面外形变化

4个不同弹性模量下分别取8块柔性面气动面特征曲线AB上各特征点变形量，求平均值，得到特征点变形量变化曲线，如图5（a）所示。由计算结果可知，当柔性面的弹性模量为50GPa时，柔性面上最大变形出现在沿径向方向的中部，最大位移量约为13.8mm，柔性面上缘至柔性面中部的位移量随径向方向逐渐增大，增长速率递减，柔性面中部至柔性面外缘的位移量先减后增，变化幅度不大，柔性面最外缘面外位移较大，最大位移量约为13.6mm；当柔性面的弹性模量为5GPa/0.5GPa时，柔性面变形量沿径向方向先增后减再增，最大变形位置为柔性面外缘；50MPa时，柔性面的变形量沿径向增加，中间段增幅缓慢，内外缘处增幅较大，最大变形量在柔性面外缘为53mm。特征曲线CD上，由计算结果可以看出，最大的面外位移出现在相邻辐条支撑的每块柔性面的平分线上，如图5（b）所示。整体情况为每块柔性面中部形成一个凹陷，此外，柔性面最外缘部分的变形量也较明显。在工程实践中，由于机械展开的运动形式，柔性面在展开到规定气动面位置时柔性面上存在一定的预紧力，会减小变形。柔性面的位移量随材料的弹性模量的减小依次递增，特征曲线上各点的变形量变化趋势类似，在弹性模量为0.5GPa时变形量已经达到了接近30mm，变形量较大，将会带来的气动加热显著等问题。

3.3 结构应力

选取动压最大时刻进行计算，特征曲线AB上各点拉应力随位置变化曲线如图6（a）所示。特征曲线EF上各位置点拉应力如图6（b）所示：

图5 特征线AB/CD变形量曲线图

由图6可知，刚性头锥和柔性面连接处的拉应力最大，最大拉应力出现在刚柔交接处的中部位置，在特征曲线AB上，拉应力大小随径向方向持续减小，开始下降较快，中部位置压应力下降不明显，外缘处应力较小。当材料的弹性模量为50GPa时，最大拉应力大小为5MPa。特征曲线EF上，弹性模量为50GPa时每块柔性面与柔性面连接处的应力出现先减后增的趋势，刚柔交界处拉应力最大，为3.5MPa，前半段下降趋势明显，特征线EF中部最小拉应力为1MPa，随后持续增大至3.2MPa。5GPa的弹性模量下，拉应力也是先减后增，最大拉应力为1.6MPa。当柔性面的弹性模量为500MPa时，最大拉应力在0.6MPa以下。

3.4 厚度影响

柔性面的厚度也是影响气动面变形的关键因素之一。机械展开式再入飞行器的柔性面包括迎风面的烧蚀层、隔热层，背风面的承载层，本文所用流固耦合模型只研究承载层。本文模型中设置柔性面初始厚度为2mm。根据上文计算结果，当柔性面材料的弹性模量介于5至50GPa时柔性面的变形量较小，所以选择弹性模量为25GPa的状态进行厚度的对比分析，柔性面厚度分别取为1mm和2mm。由图7可以看出，当柔性面的厚度从2mm变成1mm后，特征曲线AB上各点的变形趋势不变，最大变形量由14.7mm增加至23mm，是原来的1.5倍左右。

4 结束语

本文通过对机械展开式再入飞行器的气动面进行流固耦合研究，建立了三维非定常环境下机械展开式再入飞行器气动面的流固耦合数值模型，对比柔性面材料不同的弹性模量参数，得出柔性面的变形和应力随弹性模量的变化关系，以及柔性面厚度对变形量的影响，结论如下：

1）随着材料弹性模量的减小，变形量增加显著，弹性模量为50GPa左右时变形量较小；

2）气动面稳定后，每块柔性面的最大变形出现在柔性面的外缘处，柔性面中部形成一个向内的凹坑，其最大变形量与外缘处最大扰度相差不大；

3）柔性面受气动载荷作用下，头锥与柔性面连接处的局部拉应力最大，需要提高该连接处的强度，此外，在弹性模量为5至50GPa状态下肋条和柔性面连接的地方，应力两端大、中部小；

4）当柔性面的厚度从2mm变成1mm后，最大变形量由14.7mm增加至23mm，是原来的1.5倍左右。

[1] 李旭东. 半刚性机械展开式进入飞行器特性分析[D]. 南京: 南京航空航天大学, 2015. LI Xudong. The Analysis of Characteristics for Semi-rigid Mechanically-deployed Entry Decelerator[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015. (in Chinese)

[2] STERN E, BARNHARDT M, VENKATAPATHY E, et al. Investigation of Transonic Wake Dynamics for Mechanically Deployable Entry Systems[C]//IEEE Aerospace Conferenc. Big Sky, MT, IEEE, 2012: 53(7): 1-10. DOI: 10. 1109/AERO. 2012. 6187000.

[3] DUTTA S, SMITH B, PRABHU D, et al. Mission Sizing and Trade Studies for Low Ballistic Coefficient Entry Systems to Venus [C]//IEEE Aerospace Conferenc. Big Sky, MT, IEEE, 2012: 186(6): 1-14.

[4] VENKATAPATHY E, AMOLD J, FERNANDEZ I, et al. Adaptive Deployable Entry and Placement Technology (ADEPT): A Feasibility Study for Human Mission to Mars[C]//21st AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Reston, USA: AIAA, 2011. AIAA-2011-2608.

[5] AMOLD J, PETERSON K H, YOUNT B C, et al. Thermal and Structural Performance of Woven Carbon Cloth for Adaptive Deployable Entry and Placement Technology[C]//AIAA Aerodynamic Decelerator Systems Conference. Reston, USA: AIAA 2013, 46(2): 251-252.

[6] 高艺航, 贺卫亮. 充气式返回舱气动热特性研究[J]. 航天返回与遥感, 2014, 35(4): 17-25. GAO Yihang, HE Weiliang. Research on Aerodynamic Heating Characteristics of Inflatable Reentry Decelerator[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(4): 17-25. (in Chinese)

[7] 荣成成, 左光, 陈冲, 等. 充气式再入航天器总体方案及关键技术初探[J]. 航天返回与遥感, 2015, 36(1): 16-23. RONG Chengcheng, ZUO Guang, CHEN Chong, et al. A Study of General Scheme and Key Technologies of Inflatable Re-entry Vehicle[J]. Spacecraft Recovery & Remote Sensing, 2015, 36(1): 16-23. (in Chinese)

[8] 卫剑征, 谭惠丰, 王伟志, 等. 充气式再入减速器研究最新进展[J]. 宇航学报, 2013, 34(7): 881-890. WEI Jianzheng, TAN Huifeng, WANG Weizhi, et al. New Trends in Inflatable Re-entry Aeroshell[J]. Journal of Astronautics, 2013, 34(7): 881-890. (in Chinese)

[9] 李旭东, 张鹏, 尚明友, 等. 基于金星探测机械展开式进入飞行器技术述评[J]. 航天返回与遥感, 2015, 36(2): 1-8. LI Xudong, ZHANG Peng, SHANG Mingyou, et al. Review of Venus Explorer Mission Using Mechanically-deployed Entry Decelerator[J]. Spacecraft Recovery & Remote Sensing, 2015, 36(2): 1-8. (in Chinese)

[10] VENKATAPATHY E, PETERSON K H, BLOSSER M L, et al. Viability of 3D Woven Carbon Cloth and Advanced Carbon-carbon Ribs for Adaptive Deployable Entry Placement Technology (ADEPT) for Future NASA Missions[C]//National Space and Missiles Symposium, June 24-28, 2013, Bellevue , Washington: AIAA.

[11] COOK G, ZHANG Z C, IM K. Applications of the CESE Method in LS-DYNA[C]//21st AIAA Computational Fluid Dynamics Conference, June 24-27, 2013, San Diego, CA.

[12] 赵书苗. 时-空守恒元解元方法数值研究[D]. 西安: 西北工业大学, 2007. ZHAO Shumiao. The Numerical Study of The Space-time Conservation Element and Solution Element Method[D]. Xian: Northwestern Polytechnical University, 2007. (in Chinese)

[13] ZHANG Z C, COOK G. New Features of CE/SE Compressible Fluid Solver in LS-DYNA[C]//13th International LS-DYNA Users Conference.

[14] 邢景棠, 周盛, 崔尔杰. 流固耦合力学概述[J]. 力学进展, 1997, 27(1): 19-38. XING Jingtang, ZHOU Sheng, CUI Erjie. A Survey on the Fluid Solid Interaction Mechanics[J]. Advances in Mechanics, 1997, 27(1): 19-38. (in Chinese)

[15] 高兴龙, 唐乾刚, 张青斌, 等. 开缝伞充气过程流固耦合数值研究[J]. 航空学报, 2013, 34(10): 2270. GAO Xinglong, TANG Qiangang, ZHANG Qingbin, et al. Numerical Study on Fluid-structure Interaction of Slot-parachute’s Inflation Process[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(10): 2270. (in Chinese)

[16] HUANG Yuying, QIAN Qin, WANG Shigang, et al. Fluid-structure Impact Analysis with a Mixed Method of Arbitrary Lagrangian-eulerian BE and FE[J]. Acta Mechanica Solida Sinica, 1993, 41(993): 365-376.

[17] 陈锋, 王春江, 周岱. 流固耦合理论与算法评述[J]. 空间结构, 2012, 18(4): 58-59. CHEN Feng, WANG Chunjiang, ZHOU Dai. Review of Theory and Numerical Methods of Fluid-structure Interaction[J]. Spatial Structures, 2012, 18(4): 58-59. (in Chinese)

[18] 陈宇峰, 陈务军, 赵飞龙, 等. ETFE 膜材泊松比对膜结构变形的影响分析[J]. 科学技术与工程, 2013, 13(5): 4246-4251. CHEN Yufeng, CHEN Wujun, ZHAO Feilong, et al. Impact Analysis of ETFE Membrane Poisson’s Ratio on Membrane Structural Deformation[J]. Science Technology and Engineering, 2013, 13(5): 4246-4251. (in Chinese)

（编辑：毛建杰）

Simulation Analysis of Mechanical Properties of Mechanically-deployed Entry Decelerator with Flexible Surface

DONG Xin ZHANG Hongying CHEN Jianping

（Ministerial Key Discipline Laboratory of Advanced Design Technology of Aircraft, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China）

Aiming at the task demand of China's future reentry and deep space exploration, the research on mechanically-deployed entry decelerator is carried out. Based on the structural characteristics of the mechanically-deployed entry decelerator, the numerical model of the fluid-solid coupling of the aerodynamic surface of the entry decelerator in the three-dimensional unsteady environment is established usingthe space-time conservation element and solution element method. The deformation and stress of the flexible surface are analyzed by comparing the material modulus of elasticity in numerical simulation. The following conclusions can be get through comparative analysis: A more visible vortex appears on the back of the decelerator, which inhibits the deformation of the flexible surface. The modulus of elasticity range of the flexible material, the distribution and size of the deformation and stress, and the influence of the thickness of the flexible surface on the deformation can be get by analysis. It meets the requirements when the elastic modulus of the flexible plane is about 50GPa. The maximum deformation position lies at the edge of the flexible surface. The middle of the flexible surface forms an inward depression, and its maximum variable shape is smaller than the amount of deformation of the edge. The effect of the thickness of flexible surface on the deformation is also discussed .The results of this paper provide the basis for the aerodynamic characteristics and aerodynamic heating analysis of the flexible surface, and also provides reference for the engineering development of the flexible surface.

entry decelerator; mechanically-deployed; fluid-structure coupling; flexible material; spacecraft recovery

V525

A

1009-8518(2018)01-0011-08

10.3969/j.issn.1009-8518.2018.01.002

董鑫，男，1993年生，南京航空航天大学航空宇航学院航空工程专业硕士研究生，研究方向为航天器返回技术。E-mail: 1529987531@qq.com.

2017-04-24

航空科学基金（2016ZC52031），江苏高校优势学科建设工程资助项目