载人飞船两种垂挂转换方案载荷比较及分析
包进进 雷江利 贾贺
载人飞船两种垂挂转换方案载荷比较及分析
包进进1,2雷江利1贾贺1
(1 北京空间机电研究所,北京 100094)(2 北京市航空智能遥感装备工程技术研究中心,北京 100094)
为了对新一代载人飞船转垂挂载荷进行深入研究,优化结构设计,文章首先建立了转垂挂过程的动力学模型,通过与空投试验结果比对验证了模型的正确性。在此基础上,针对标称工况、主伞阻力面积偏小工况、返回舱质量偏大工况,计算得到无阻尼缓冲装置和有阻尼缓冲装置两种转垂挂方案对应垂挂转换过程中垂挂吊带载荷及返回舱过载。结果表明:最小载荷出现在主伞阻力面积偏小工况下,最大载荷出现在返回舱质量偏大工况下;各种工况下,阻尼缓冲装置对降低垂挂转换过程中的过载能起到一定的效果;载荷越大的工况阻尼缓冲装置的缓冲效果越差。文章的建模方法和分析结果对新一代大载重载人飞船的论证有一定借鉴意义。
拉力 过载 阻尼缓冲装置 垂挂吊带 垂挂转换 载人飞船
0 引言
为了降低载人飞船的着陆过载,消除对航天员的冲击伤害,在采用降落伞减小载人飞船下降速度方案的基础上,需配合采用反推发动机或着陆缓冲气囊的方案,实现将载人飞船着陆过载控制在航天员可接受范围内。反推发动机或缓冲气囊均布置在飞船防热大底内部、返回舱正下方,而降落伞吊点一般布局在返回舱侧壁靠近顶端,在降落伞减速阶段采用单点吊挂方式工作。为了反推发动机或缓冲气囊更好的工作,在反推发动机或缓冲气囊工作前,需将降落伞吊挂方式由单点吊挂转换为双点吊挂,使反推发动机推力或气囊缓冲作用力尽量沿返回舱轴向方向。为此,飞船着陆过程中设置转垂挂程序,实现返回舱单点吊挂转为双点吊挂[1]。
在飞船垂挂转换工作过程中,将产生较大的载荷作用在垂挂吊带和返回舱结构上,随着“神舟”飞船一期及二期飞行任务的成功,对飞船转垂挂过程的吊带载荷和返回舱过载已经进行了深入的研究,并通过地面、空投试验和飞行任务的验证,表明“神舟”飞船转垂挂过程设计的正确性和合理性。目前,国内外均在加紧研制功能和性能更强的新一代载人飞船,新一代载人飞船质量比“神舟”飞船质量大很多,将采用阻力面积更大的群伞进行减速[2-4]。由于返回舱质量增加且垂挂转换的自由行程大,新一代载人飞船垂挂转换过程将可能带来更大的载荷[5],对垂挂吊带和返回舱的结构设计提出了更高要求。
为了对新一代载人飞船转垂挂载荷进行深入研究,优化结构设计,本文首先通过建立转垂挂过程的动力学模型,仿真得到垂挂转换过程中的吊带拉力及返回舱过载。为了减小吊带承受的拉力和返回舱过载,设计采用传统的减小冲击的铝蜂窝阻尼缓冲装置,通过仿真对阻尼缓冲装置工作下的转垂挂过程吊带拉力和返回舱过载进行分析。并对无阻尼缓冲装置和有阻尼缓冲装置两种方案的载荷进行比对。本文的建模方法和分析结果对新一代大载重载人飞船的论证有一定借鉴意义。
1 动力学模型及模型验证
1.1 基本假设
在飞船转垂挂过程中,受力情况十分复杂,为了简化计算过程,对计算模型进行如下假设:
1)主降落伞和返回舱在每一瞬时的运动都遵循同一条轨迹,且运动方向与重力方向相同;
2)考虑重力、气动力、伞带拉力;
3)考虑主伞结构质量和附加质量[6-7];
4)阻尼缓冲装置工作过程垂挂吊带按恒定拉力计算;
5)伞带在拉伸过程中的受力严格按照其材料试验获得的静态应力—应变曲线[8];
6)不考虑主伞运动过程中的扭矩。
1.2 动力学模型
本仿真所建动力学模型将主伞伞衣、主伞伞绳和主伞吊带视为一个质点,将返回舱视为一个质点,将主伞伞绳、主伞吊带和垂挂吊带等效为一根柔性带[9-10],称为伞带。动力学模型如图1所示。
根据图1建立的动力学模型如下
ds/d=(s-ds)/s+n,ds/d=s(1)
dc/d=(-dc-s)/c+n,dc/d=c(2)
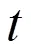
s=×,>0 (3)
式中为中间变量,=(sl×bl×bh×(sl+bl+bh))/(bl×bh×slsl×bh×blsl×bl×bh),其中sl、bl、bh依次为主伞伞绳、主伞吊带、垂挂吊带断裂强度;为伞带总伸长率,(sl+bl+bh-(sl+bl+bh))/(sl+bl+bh),其中sl、bl、bh依次为主伞伞绳、主伞吊带、垂挂吊带未变形前原长,sl、bl、bh依次为物伞系统运动过程中主伞伞绳、主伞吊带、垂挂吊带伸长后实际长度。
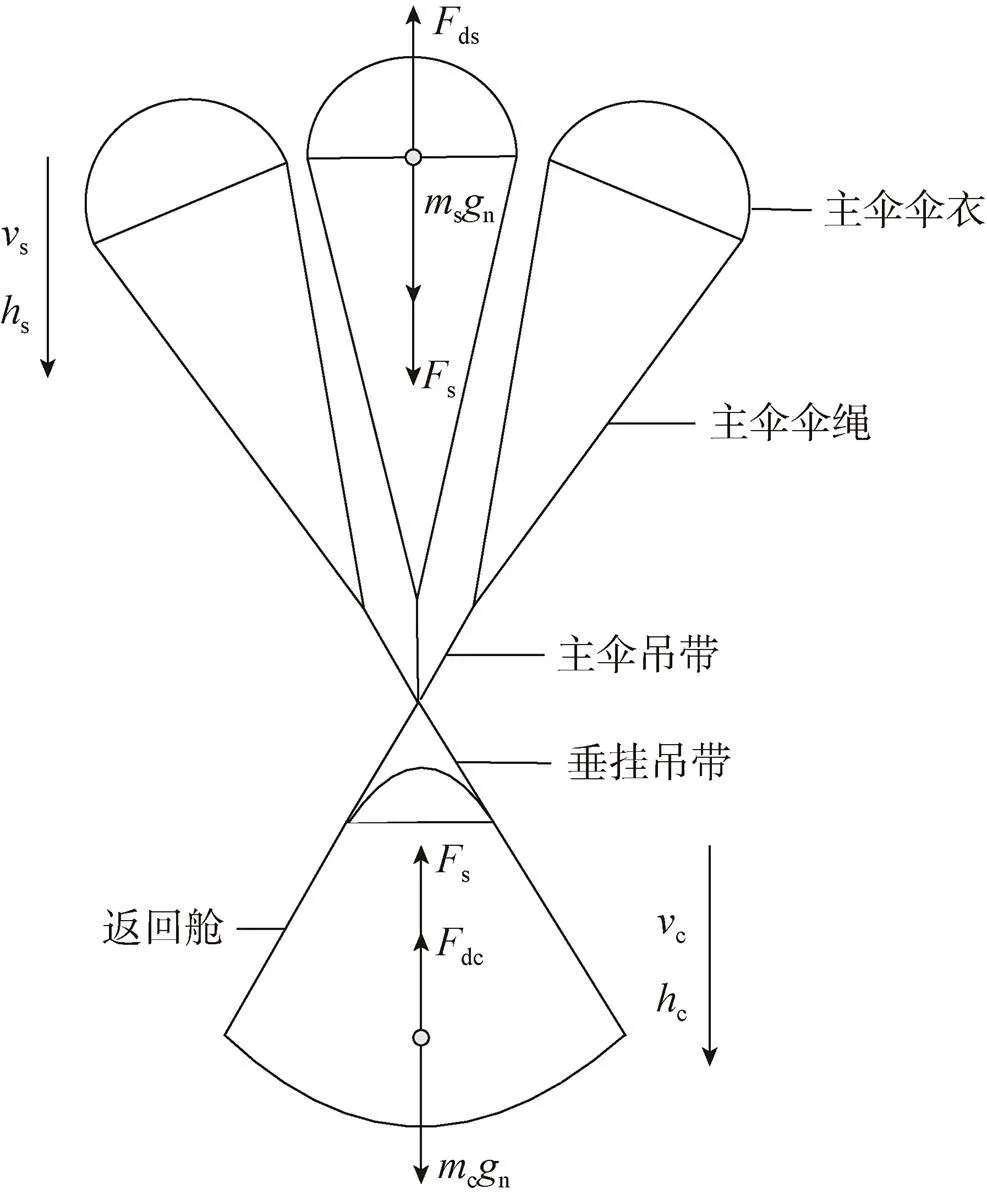
图1 动力学模型
在上述动力学模型基础上,考虑阻尼缓冲装置的动力学模型应为:在上述动力学模型基础上,将垂挂转换过程分为两个阶段,第一个阶段为单点吊挂转为双点吊挂阶段,实际仿真过程中在此阶段考虑垂挂吊带拉脱防热层阶段(拉防热层阶段认为伞带拉力为定值,s取定值,即取为防热层拉脱力);第二个阶段为阻尼缓冲装置工作阶段,此阶段认为伞带的拉力为定值,s取定值,即取为阻尼缓冲装置的压溃力。
1.3 模型验证
为了验证动力学模型的正确性,利用“神舟”飞船空投试验数据与仿真结果进行比对,具体仿真结果如图2所示,试验结果如图3所示。
通过图2可以看出,垂挂吊带最大拉力仿真结果为62kN,稳降阶段拉力约为18kN,拉力变化周期约为1s。通过图3可以看出,此次空投试验垂挂吊带最大拉力约为60kN,稳降阶段的拉力约为18kN,拉力变化周期约为1s。仿真结果与试验结果基本吻合,因此认为仿真结果可信。
由于本仿真不考虑垂挂转换过程中的舱的摆动,因此仿真结果较试验结果更早趋于稳定。
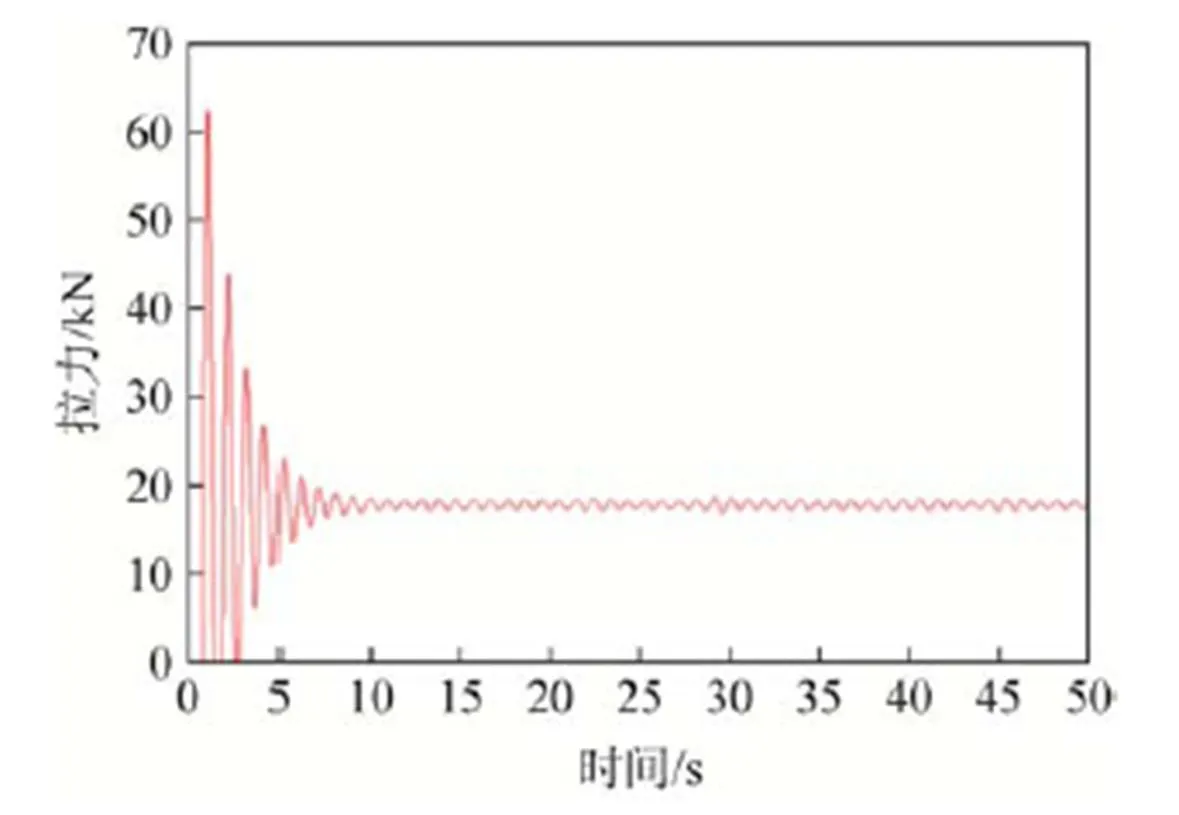
图2 仿真结果
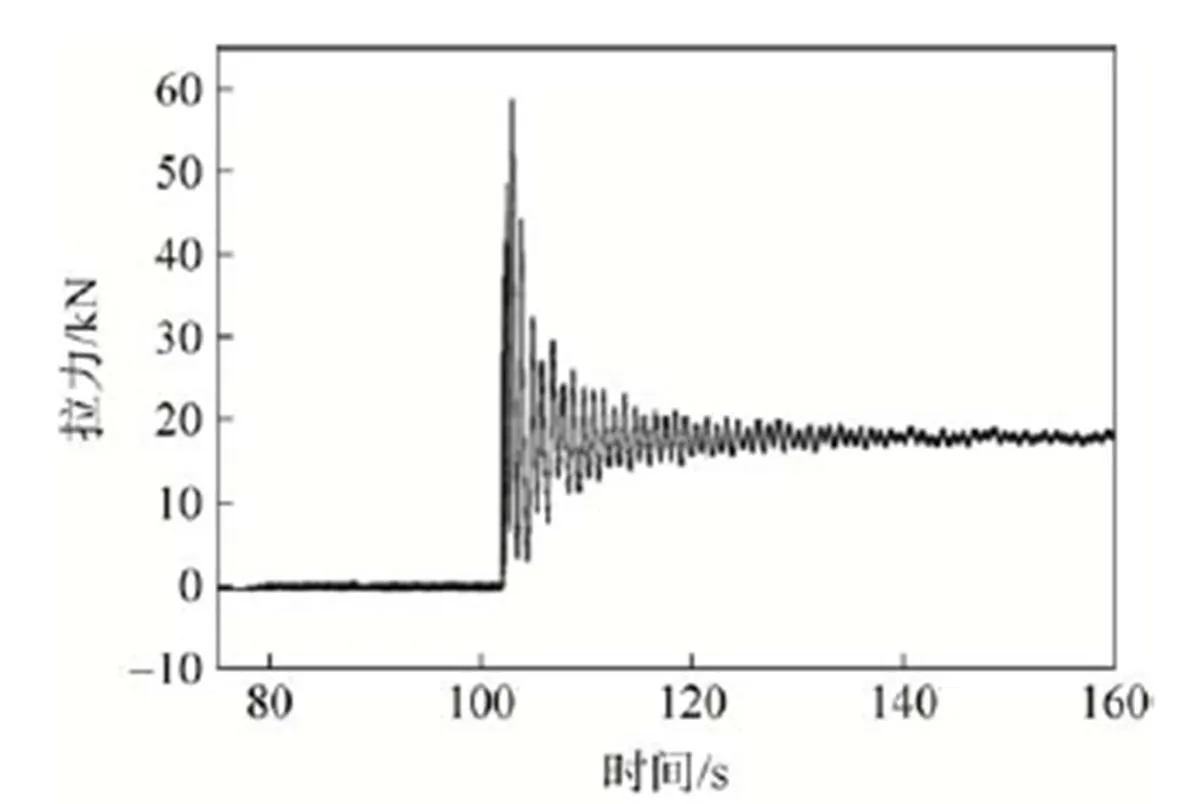
图3 试验结果
2 两种垂挂转换方案载荷比较与分析
由于传统的降低冲击的缓冲装置为铝蜂窝结构,因此本文研究无阻尼缓冲装置和采用铝蜂窝结构的有阻尼缓冲装置两种方案对应的吊带载荷及返回舱过载。两种方案具体连接形式如图4和图5所示。
新一代大载重载人飞船回收着陆过程中涉及多种工况,为了全面考察两种转垂挂方案在各工况下的工作性能,本文针对标称工况、主伞阻力面积偏小工况、返回舱质量偏大工况,分别对两种转垂挂方案下的吊带载荷及返回舱过载进行仿真计算。
2.1 标称工况
标称工况下,两种转垂挂方案下的吊带载荷及返回舱过载仿真结果如图6~图9所示。
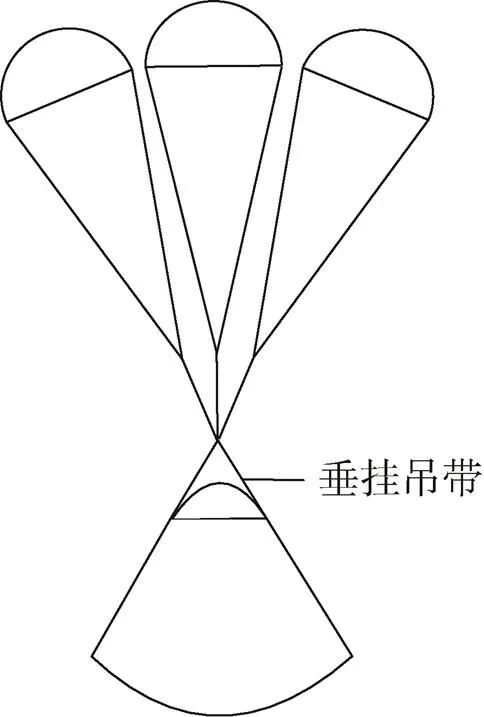
图4 无阻尼缓冲装置方案示意图
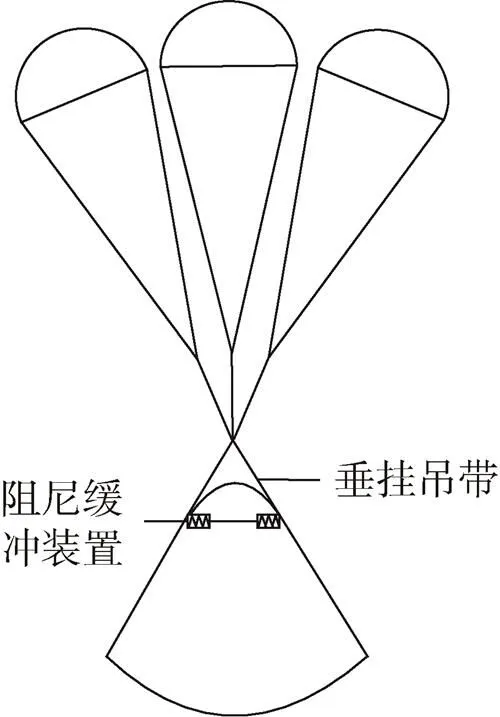
图5 有阻尼缓冲装置方案示意图
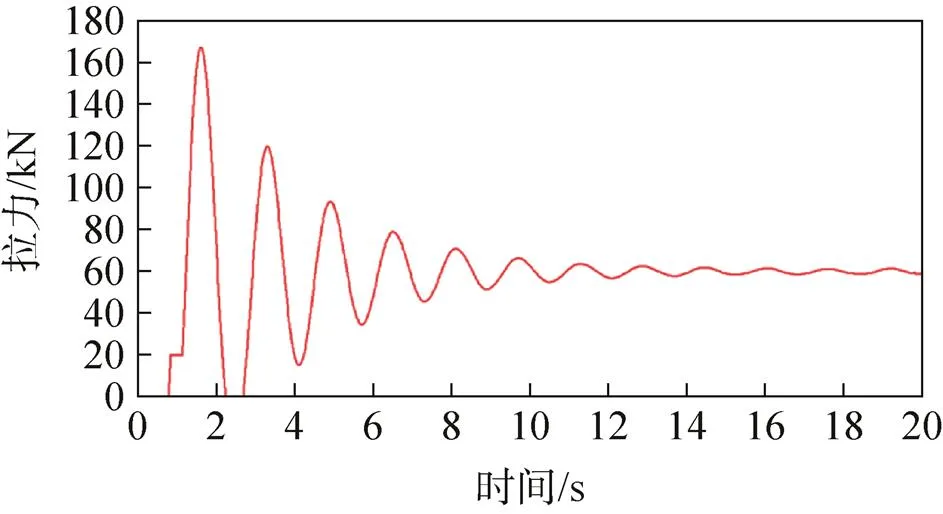
图6 无阻尼缓冲装置方案吊带拉力
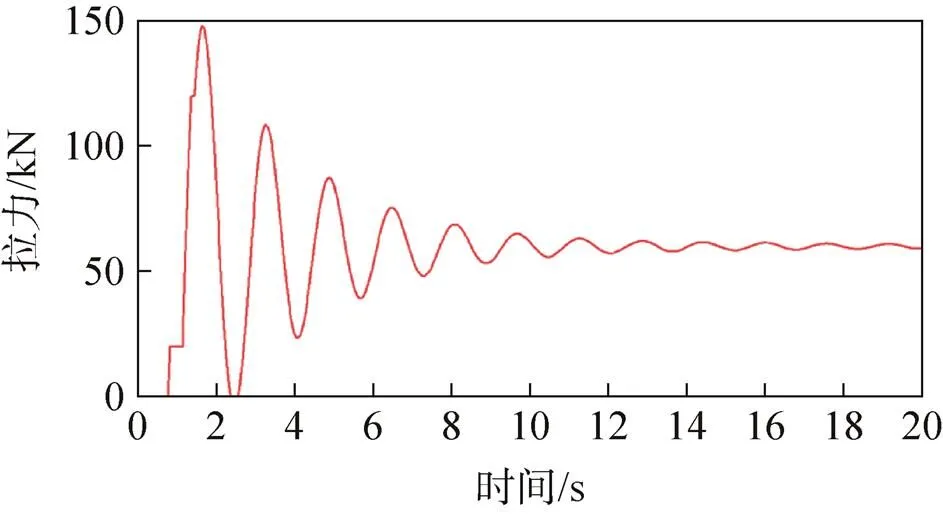
图7 有阻尼缓冲装置方案吊带拉力

图8 无阻尼缓冲装置方案返回舱过载
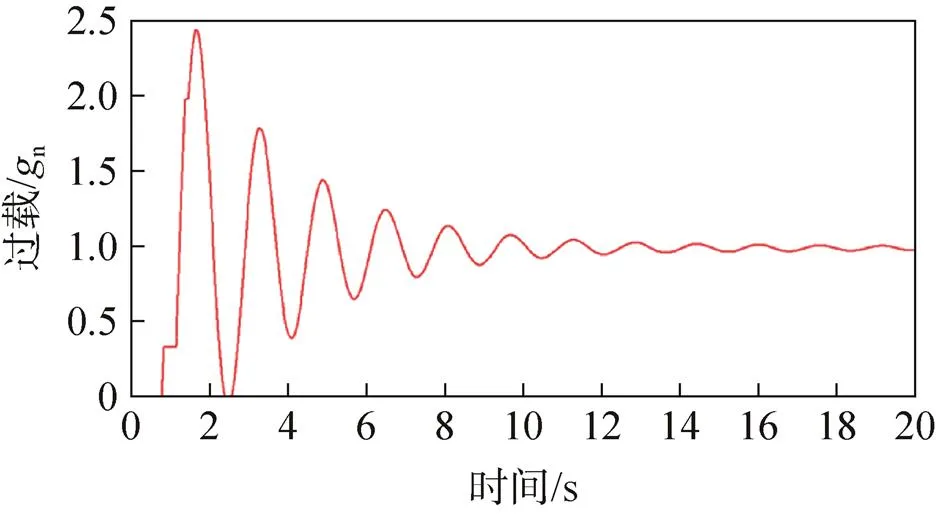
图9 有阻尼缓冲装置方案返回舱过载
根据图6、图8可以看出,无阻尼缓冲装置的转垂挂方案中两根垂挂吊带的拉力合力(沿返回舱轴线)最大值为167.39kN,返回舱最大过载为2.754 9n。根据图7、图9可以看出,有阻尼缓冲装置的转垂挂方案中两根垂挂吊带的拉力合力(沿返回舱轴线)最大值为150kN,返回舱最大过载为2.468 7n。
上述仿真结果表明:标称工况下,阻尼缓冲装置对降低垂挂转换过程中的过载能起到一定的效果。
2.2 主伞阻力面积偏小工况
主伞阻力面积偏小工况下,两种转垂挂方案下的吊带载荷及返回舱过载仿真结果如图10~图13所示。
根据图10、图12可以看出,无阻尼缓冲装置的转垂挂方案中两根垂挂吊带的拉力合力(沿返回舱轴线)最大值为158.88kN,返回舱最大过载为2.614 9n。根据图11、图13可以看出,有阻尼缓冲装置的转垂挂方案中两根垂挂吊带的拉力合力(沿返回舱轴线)最大值为142.65kN,返回舱最大过载为2.347 8n。
上述仿真结果表明:主伞阻力面积偏小工况下,阻尼缓冲装置对降低垂挂转换过程中的过载能起到一定的效果。
2.3 返回舱质量偏大工况
返回舱质量偏大工况下,两种转垂挂方案下的吊带载荷及返回舱过载仿真结果如图14~图17所示。
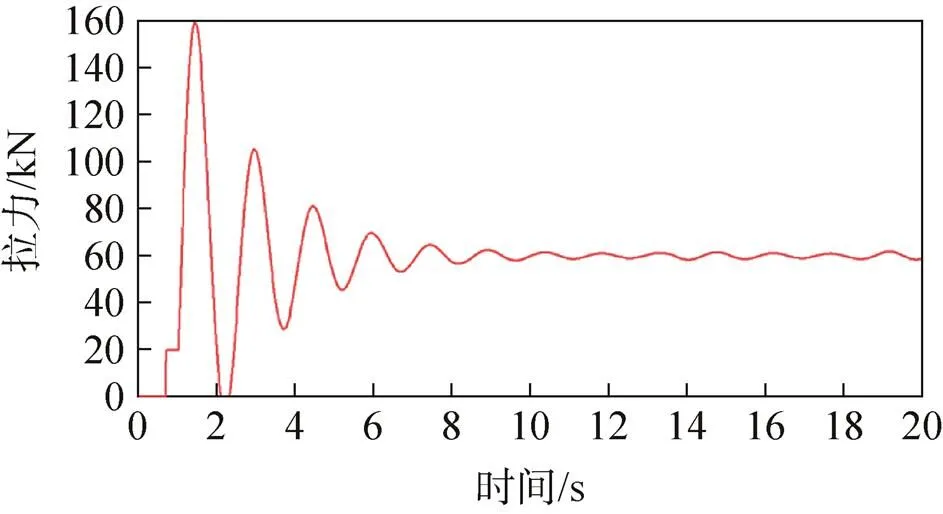
图10 无阻尼缓冲装置方案吊带拉力
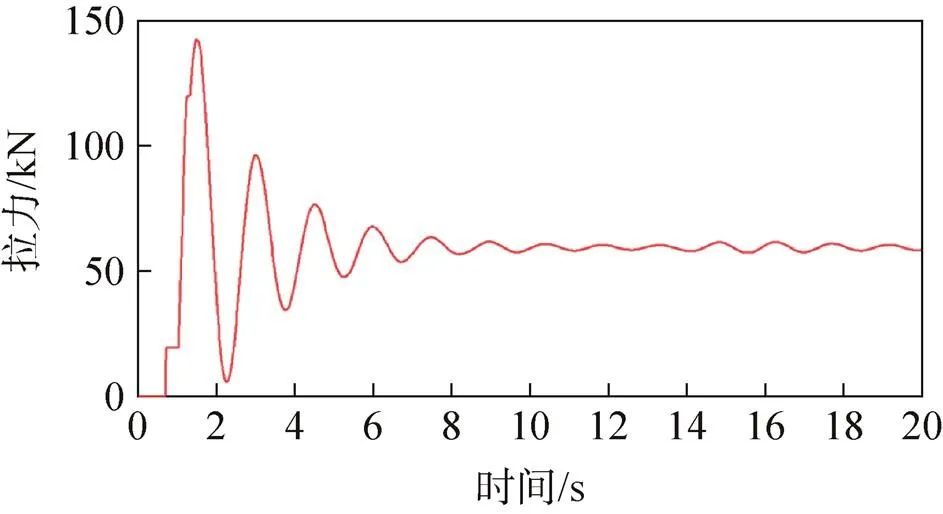
图11 有阻尼缓冲装置方案吊带拉力
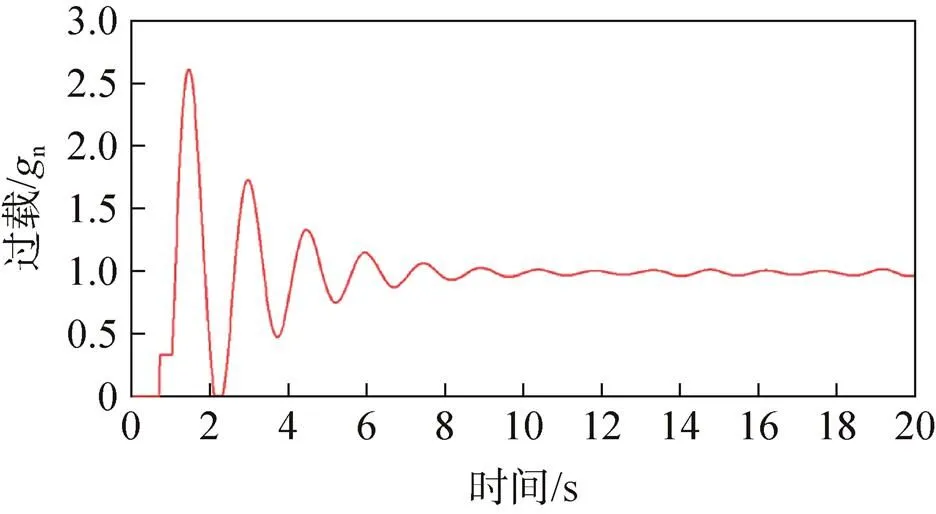
图12 有阻尼缓冲装置方案返回舱过载
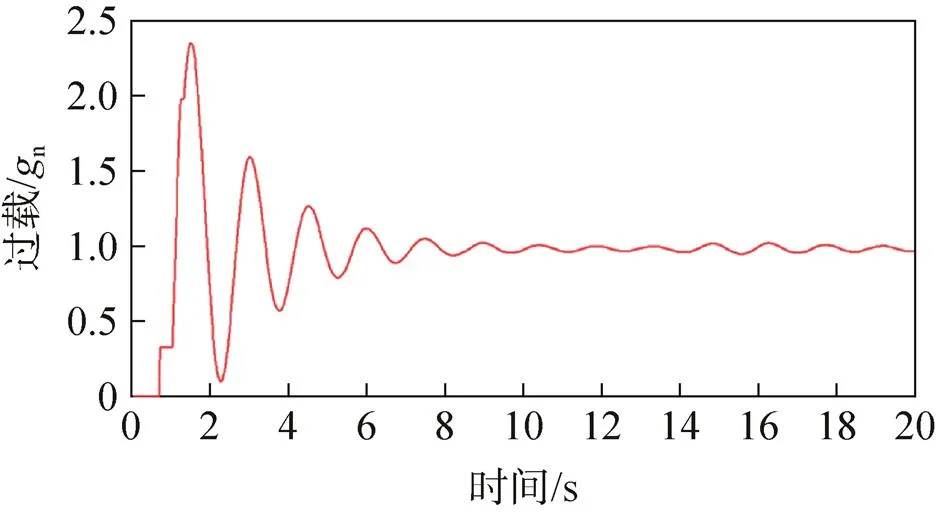
图13 无阻尼缓冲装置方案返回舱过载
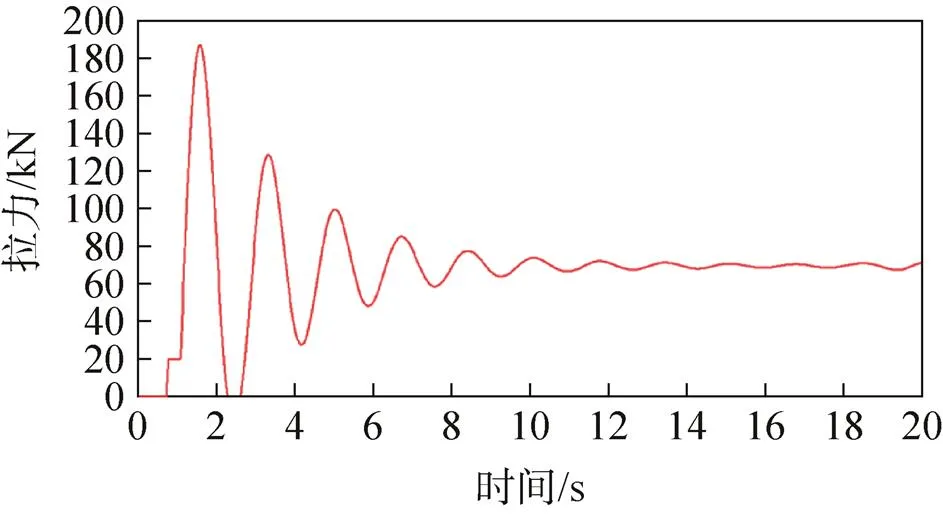
图14 无阻尼缓冲装置方案吊带拉力
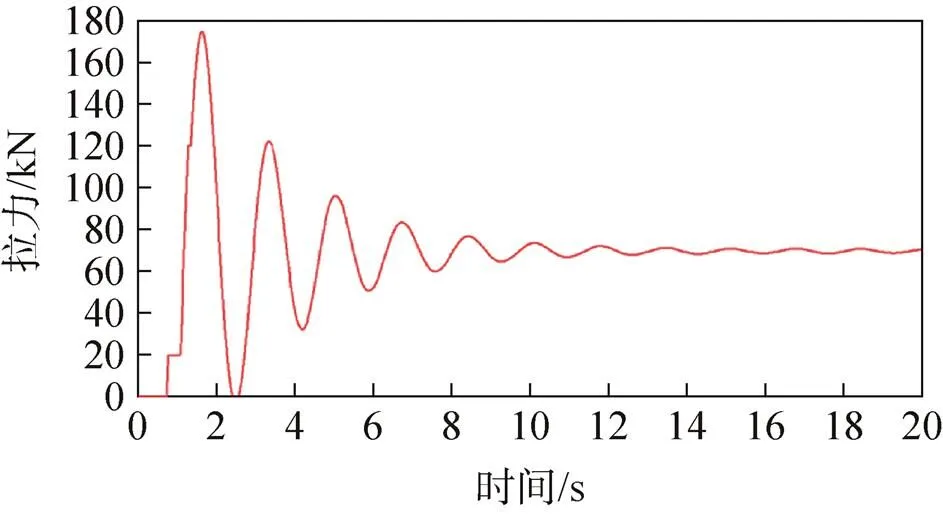
图15 有阻尼缓冲装置方案吊带拉力
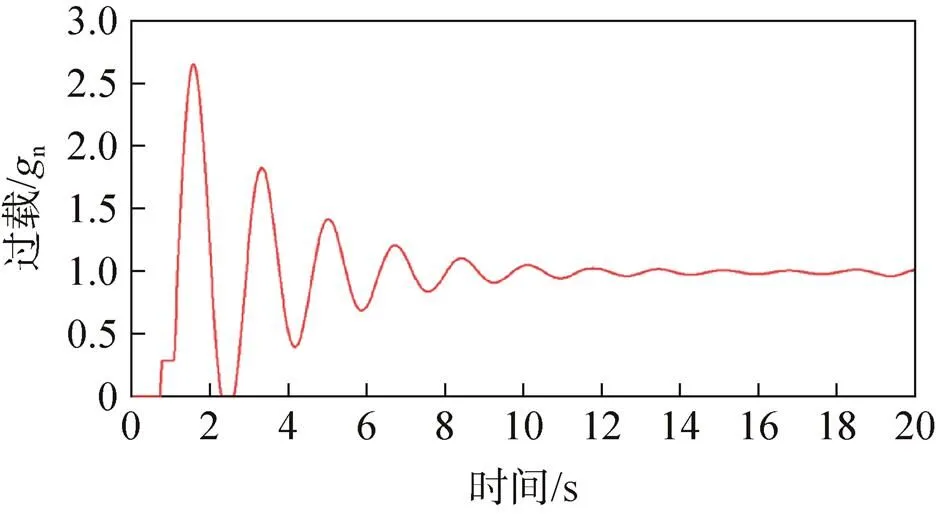
图16 无阻尼缓冲装置方案返回舱过载
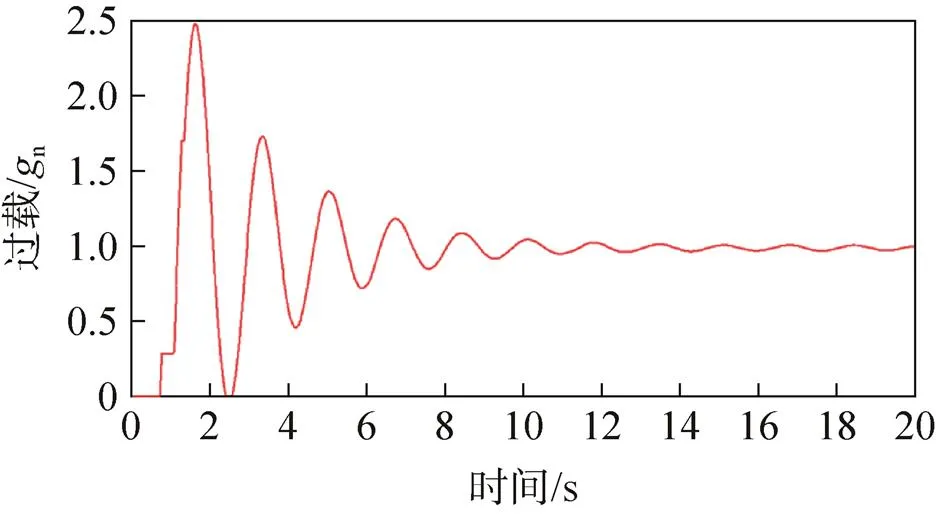
图17 有阻尼缓冲装置方案返回舱过载
根据图14、图16可以看出,无阻尼缓冲装置的转垂挂方案中两根垂挂吊带的拉力合力(沿返回舱轴线)最大值为187.03kN,返回舱最大过载为2.650 7n。根据图15、图17可以看出,有阻尼缓冲装置的转垂挂方案中两根垂挂吊带的拉力合力(沿返回舱轴线)最大值为174.76kN,返回舱最大过载为2.476 7n。
上述仿真结果表明:返回舱质量偏大工况下,阻尼缓冲装置对降低垂挂转换过程中的过载能起到一定的效果。
2.4 两种方案比较分析
根据2.1~2.3节仿真结果,比较两种方案的垂挂转换过程载荷如表1所示。
表1 两种方案对应载荷比较
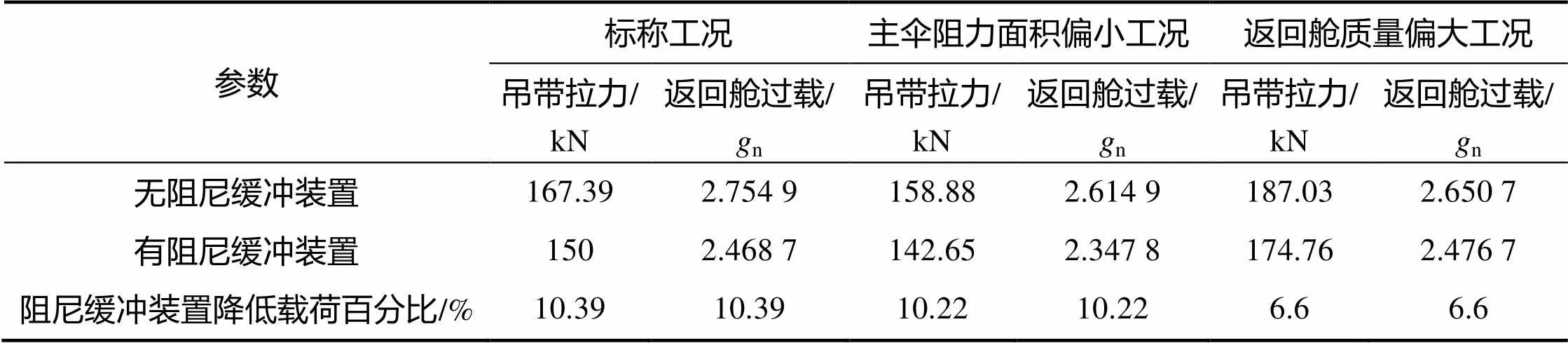
Tab.1 Load comparison of two schemes
通过表1可以看出:
1)主伞阻力面积偏小工况下,垂挂转换过程中垂挂吊带的拉力和返回舱过载与其他两种工作模式比较最小;返回舱质量偏大工况下,垂挂转换过程中垂挂吊带的拉力和返回舱过载与其他两种工作模式比较最大;
2)各种工况下,阻尼缓冲装置对降低垂挂转换过程中的过载能起到一定的效果,加阻尼缓冲装置降低载荷百分比在6.6%~10.39%之间;
3)由于缓冲行程不变,使得载荷越大的工况下阻尼缓冲装置的缓冲效果越差。
3 结束语
本文针对标称工况、主伞阻力面积偏小工况、返回舱质量偏大工况,研究了无阻尼缓冲装置和有阻尼缓冲装置两种转垂挂方案对应垂挂转换过程中垂挂吊带载荷及返回舱过载。通过分析仿真结果得出以下结论:
1)最小载荷出现在主伞阻力面积偏小工况下,最大载荷出现在返回舱质量偏大工况下;
2)各种工况下,阻尼缓冲装置对降低垂挂转换过程中的过载能起到一定的效果,为了提高缓冲效率,后续需要对缓冲行程和蜂窝性能进行优化设计;
3)载荷越大的工况阻尼缓冲装置的缓冲效果越差。
由于转垂挂过程时间较短,本文的建模过程未考虑返回舱姿态的变化,为了更深入的对新一代载人飞船垂挂转换过程载荷进行系统研究,后续需要开展考虑返回舱姿态的垂挂转换过程仿真工作。
[1] 童旭东, 李惠康, 葛玉君, 等. 神舟号载人飞船回收着陆分系统设计与性能评估[J]. 航天返回与遥感, 2004, 25(3): 1-5. TONG Xudong, LI Huikang, GE Yujun, et al. Design and Performance Evaluation of ‘SZ’ Manned Spacecraft Recovery and Landing System[J]. Spacecraft Recovery & Remote Sensing, 2004, 25(3): 1-5. (in Chinese)
[2] 杨雷, 张柏楠, 郭斌, 等. 新一代多用途载人飞船概念研究[J]. 航空学报, 2015, 36(3): 703-713.YANG Lei, ZHANG Bainan, GUO Bin, et al. Concept Definition of New-generation Multi-purpose Manned Spacecraft[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(3): 703-713. (in Chinese)
[3] 陈怡, 闫大庆. 国外新一代载人飞船研制概况[J]. 中国航天, 2015, (10): 18-23. CHEN Yi, YAN Daqing. Overview of New Generation of Manned Spacecraft[J]. Aerospace China, 2015, (10): 18-23. (in Chinese)
[4] 庞之浩. 美国研制中的几种载人天地往返系统[J]. 国际航空, 2014, (7): 31-37. PANG Zhihao. U.S. Manned Spacecraft Developing in Progress[J]. International Aviation, 2014, (7): 31-37. (in Chinese)
[5] 张家琦, 马逵. 一种特殊用途垂挂吊索钢丝绳的研发试制[J]. 热加工工艺, 2011, 40(18): 8-10.ZHANG Jiaqi, MA Kui. Research Development and Pre-production of Wire Rope of Hang Down Suspender with Special Use[J]. Hot Working Technology, 2011, 40(18): 8-10. (in Chinese)
[6] 黄伟. 降落伞附加质量的计算方法[J]. 航天返回与遥感, 2016, 37(2): 42-50. HUANG Wei. Calculation Methods of Added Mass of Parachute[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(2): 42-50. (in Chinese)
[7] 熊菁, 秦小波, 程文科. 降落伞系统附加质量的研究[J]. 中国空间科学技术, 2002, 22(4): 32-38. XIONG Jing, QIN Xiaobo, CHENG Wenke. The Added Mass Research in Parachute System[J]. Chinese Space Science and Technology, 2002, 22(4): 32-38. (in Chinese)
[8] 林斌. 降落伞伞包载荷分析计算[J]. 航天返回与遥感, 2005, 26(1): 14-17. LIN Bin. Load Analysis for Parachute Bag[J]. Spacecraft Recovery & Remote Sensing, 2005, 26(1): 14-17. (in Chinese)
[9] 王利荣. 降落伞理论与应用[M]. 宇航出版社, 1997: 318-319. WANG Lirong. Parachute Theory and Application[M]. China Astronautic Publishing House, 1997: 318-319. (in Chinese)
[10] EWING E G, BIXBY H W. 回收系统设计指南[M]. 吴天爵, 马宏伟, 译. 航空工业出版社, 1988: 225-242. EWING E G, BIXBY H W. Recovery Systems Design Guide[M]. Translated by: WU Tianjue, MA Hongwei. Aviation Industry Press, 1988: 225-242. (in Chinese)
[11] GREENE G C, PREISSER J S. Effect of Suspension Line Elasticity on Parachute Loads[J]. Journal of Spacecraft & Rockets, 1970, 7(10): 1278-1280.
[12] MOULIN J. Recovery System Simulation: Link Modelization[C]//AIAA 12thAerodynamic Decelerator Systems Technology Conference and Seminar, Lodon, United Kingdom, 1993: 296-304.
[13] 余莉, 史献林, 袁文明. 牵顶伞在降落伞拉直过程中的作用[J]. 南京航空航天大学学报, 2009, 41(2): 198-201. YU Li, SHI Xianlin, YUAN Wenming. Effects of Parachute Deployment Using Attached Apex Drogue[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2009, 41(2): 198-201. (in Chinese)
[14] 王从磊, 孙建红, 喻东明. 阻力伞拉直过程的影响因素分析[J]. 南京航空航天大学学报, 2013, 45(2): 196-201. WANG Conglei, SUN Jianhong, YU Dongming. Analysis of Effect Factors on Deployment of Drag Parachute[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(2): 196-201. (in Chinese)
[15] 鲁媛媛, 荣伟, 吴世通. 火星环境下降落伞拉直过程的动力学建模[J]. 航天返回与遥感, 2014, 35(1): 29-36.LU Yuanyuan, RONG Wei, WU Shitong. Dynamic Modeling of Parachute Deployment in Mars Environment[J]. Spacecraft Recovery & Remote Sensing, 2014, 35(1): 29-36. (in Chinese)
[16] 张青斌, 彭勇, 程文科, 等. 降落伞拉直过程的质量阻尼弹簧模型[J]. 弹道学报, 2003, 15(1): 31-36. ZHANG Qingbin, PENG Yong, CHENG Wenke, et al. A Mass Spring Damper Model of Parachute Deployment[J]. Journal of Ballistics, 2003, 15(1): 31-36. (in Chinese)
[17] 宋旭民, 秦子增, 程文科, 等. 具有倒“Y”型吊挂的降落伞系统动力学建模[J]. 国防科技大学学报, 2005, 27(5): 103-106. SONG Xumin, QIN Zizeng, CHENG Wenke, et al. The Dynamic Model of a Parachute System with the Inverted ‘Y’ Suspension[J]. Journal of National University of Defense Technology, 2005, 27(5): 103-106. (in Chinese)
[18] 张青斌, 程文科, 彭勇, 等. 降落伞拉直过程的多刚体模型[J]. 中国空间科学技术, 2003, 23(2): 45-50. ZHANG Qingbin, CHENG Wenke, PENG Yong, et al. A Multi-rigid-body Model of Parachute Deployment[J]. Chinese Space Science and Technology, 2003, 23(2): 45-50. (in Chinese)
(编辑:庞冰)
Load Comparison and Analysis of Two Kinds of Suspension Conversion Schemes for Manned Spacecraft
BAO Jinjin1,2LEI Jiangli1JIA He1
(1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)(2 Beijing Engineering Technology Research Center of Aerial Intelligent Remote Sensing Equipments, Beijing 100094, China)
In order to study suspension conversion load and optimize structure design for new generation manned spacecraft, the dynamic model of suspension conversion process is established in this paper, simulation model is confirmed by comparing airdrop test data. In normal working mode, reducing main parachute area mode, increasing capsule weight mode, hanging rope tension and capsule overload of suspension conversion process is obtained by hanging rope and hanging rope with buffer. Results show that minimum load occurs in reducing main parachute area mode, maximum load appears in increasing capsule weight mode, the damping buffer device has certain effect on reducing the load in all of modes. The load is larger, the buffer effect is worse. The results of this paper have certain reference significance for the demonstration of the new generation manned spacecraft.
tension; overload; buffer; hanging rope; suspension conversion; manned spacecraft
V423.5
A
1009-8518(2018)01-0028-07
10.3969/j.issn.1009-8518.2018.01.004
包进进,女,1984年生,2011年获中国空间技术研究院飞行器设计专业硕士学位,工程师。研究方向为航天器返回与着陆技术。E-mail:bjj0524@163.com。
2016-12-26
国家重大科技专项工程

