一种遥感器光轴微振动姿态解算方法
鲁之君 唐绍凡 李欢 田国梁
一种遥感器光轴微振动姿态解算方法
鲁之君1,2唐绍凡1李欢1田国梁1
(1 北京空间机电研究所,北京 100094)(2 先进光学遥感技术北京市重点实验室,北京 100094)
静止轨道高光谱遥感器积分时间较长且谱段较多,成像品质受高频微振动影响较大,若要提高空间分辨率,则需准确地对其光轴微振动进行探测,并指导稳像系统进行矫正。针对光轴微振动探测问题,文章首先提出了一种将像移探测与微振动姿态解算相结合的探测方法,可对遥感器光轴沿俯仰、滚转方向高频微振动进行探测;其次以符合空间分辨率要求的遥感图像作为参考图像,基于摄影测量方法建立了一系列与参考图像存在确定光轴姿态差的测试图像,将参考图像与测试图像作为输入,并对其采样间光轴姿态差进行解算;最后对仿真结果进行了分析,由仿真结果可知该方法可以有效地对10μrad以下的光轴微振动进行探测。
静止轨道 微振动 像移 摄影测量 高光谱 航天遥感
0 引言
高时效性及持续探测能力的地球静止轨道高光谱探测技术具有“图、谱、构、时”的独特优势,已成为当前高光谱遥感领域重要的发展方向。地球静止轨道高光谱遥感器的轨道高度较高、探测谱段较多,因此为了满足成像对所需能量的要求,所需的积分时间一般超过10ms,而随着积分时间的增加,遥感器所受微振动将对成像造成很大的影响[1]。随着光学遥感技术的发展,各种稳像技术层出不穷,然而无论是机械稳像[2-3]还是电子稳像[4]都需要准确的光轴微振动信息作为输入,因此对光轴微振动进行探测正逐渐成为高分辨率遥感领域的关注重点。
传统的光轴微振动探测方法主要包括星敏感器探测法、惯性元件件探测法。对于高频小振幅的光轴扰动,星敏感器的数据更新率过低(一般低于10Hz),无法对高频微振动导致的光轴微振动进行实时探测[5]。惯性元件中激光与光纤陀螺仪的探测精度最高,可达到μrad级别,然而其探测量为角速度,若将角速度进行积分求解偏转角度则带入误差较大,难以应用[6]。因此基于图像的探测方法成为航天微振动探测的新方向,文献[7]、[8]利用基于图像的联合变换相关方法对存在微振动的两幅遥感图像进行了仿真,计算得到的像移精度分别为0.2、0.25个像元,但并未给出由像移量进一步解算光轴微振动的相关计算方法。文献[9]利用共线方程理论,对选取的多个控制点进行分析得到了两摄像机空间姿态变化信息,但此方法在解算时需要控制点先验信息。
基于以上原因,本文提出了一种将像移探测与微振动姿态解算相结合的探测方法,实现了对高频微振动下遥感器沿俯仰、滚转方向微振动的探测。
1 微振动探测方法
光学遥感器在轨所受到的微振动主要为平动及转动产生的微振动,对成像产生主要影响的微振动为光轴在俯仰、滚转方向产生的转动微振动,平动微振动产生的影响可忽略不计[10]。卫星星体坐标系滚转俯仰方向定义如图1所示,其中轴正方向为卫星运动方向,轴指向地心,轴垂直于、所构成平面。定义卫星俯仰转动的正方向为顺时针方向,滚转转动的正方为逆时针方向。
高光谱静止轨道光学载荷视场范围一般为0.6°×0.6°。通过将部分视场分配给一个加装在光学系统中的小型面阵探测器,如图2所示,可实现光谱仪、小面阵同轴成像。
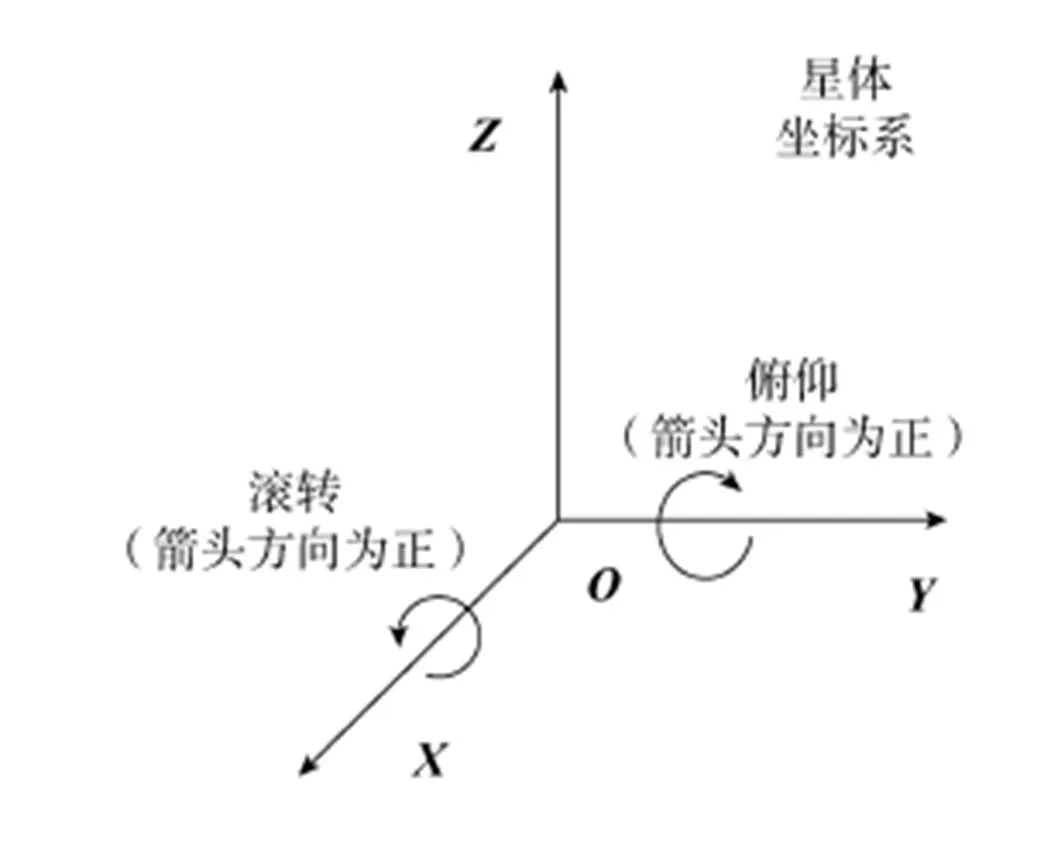
图1 卫星星体坐标系滚转、俯仰方向定义

图2 小型面阵探测器成像方式
由于光轴沿俯仰、滚转方向微振动对成像起主要影响,微振动探测方法的输出为光轴在一次积分时间内沿俯仰、滚转方向偏转量,其具体实现方法为:
1)在微振动下,首先利用小型面阵探测器在光谱仪一次积分时间内多次快速成像得到一组图像序列,并将其中相邻的图像两两分组,利用子区域像移探测方法对每组内相邻的两幅图像中多个子区域进行像移计算。小型面阵探测器构型如图3所示。
2)利用微振动姿态解算方法通过得到的多个子区域像移量对两幅图像间光轴在俯仰、滚转方向偏转量进行解算,将每组图像的光轴微振动量进行叠加,得到光谱仪一次积分时间内微振动所导致的微振动量,通过变换多个子区域的位置得到10组数据,在去除粗大误差后计算得到探测数据在俯仰、滚转方向的均值,作为最终测量。
1.1 子区域像移探测方法
子区域像移探测所用方法为联合变换相关方法[11-13],由于所选的多个子区域需要将小面阵探测器视场内的地物全部覆盖,且相互之间不可过分重叠,因此将其尺寸设定为小面阵探测器采样图像尺寸的四分之一,探测误差最小。
将存在姿态差的相邻的两幅图像定义为参考图像与目标图像,设参考图像与目标图像所对应的同一个子区域分别为,,建立平面直角坐标系–,将和的中心位置对称地置于平面直角坐标系的(–,0),(,0)点处,两者之间的物理间隔为2,如图4所示。
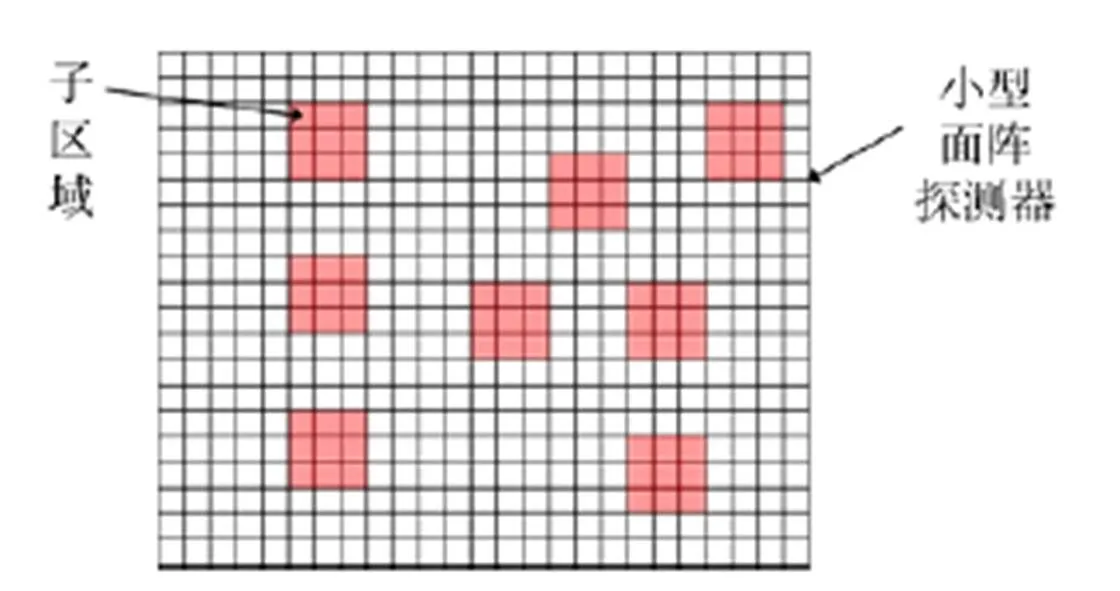
图3 小型面阵探测器构型
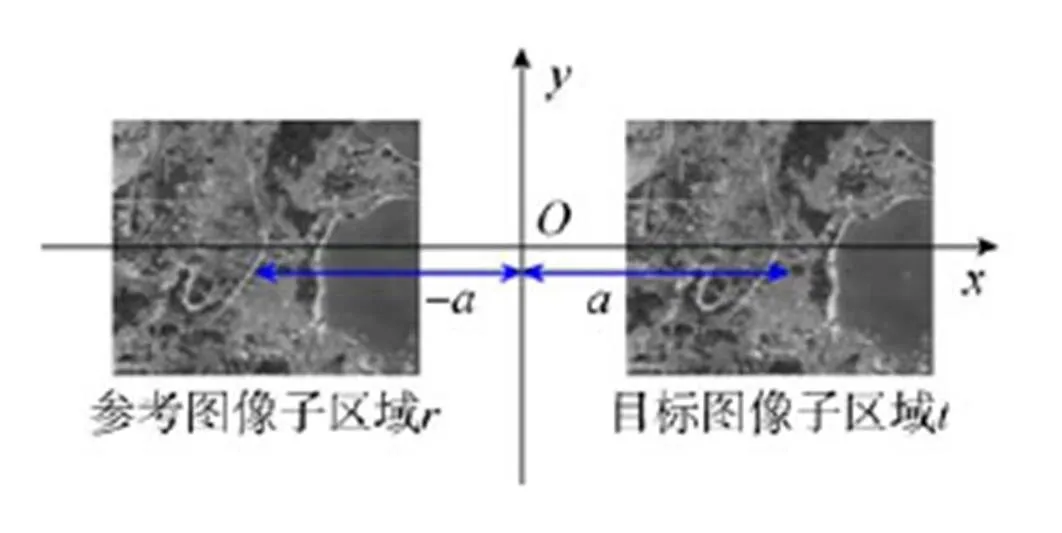
图4 输入图像放置示意
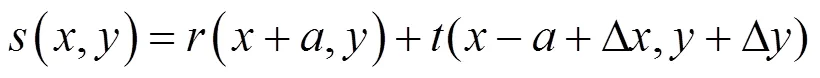
其联合功率谱为
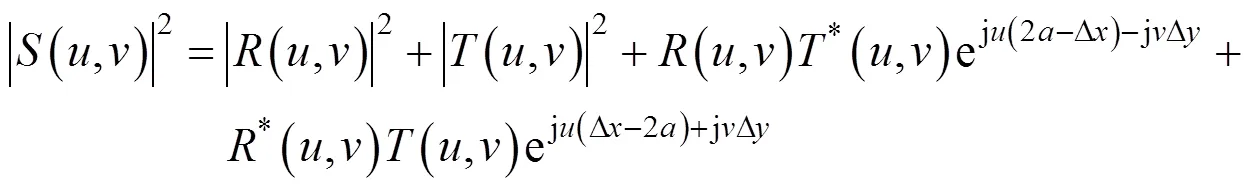
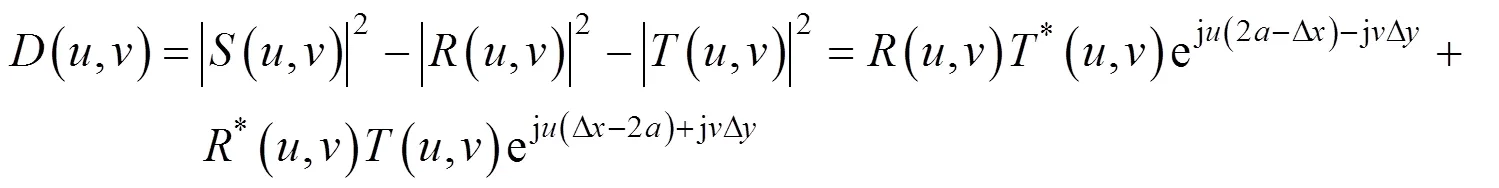
1.2 微振动姿态解算方法
微振动姿态解算方法主要目的是通过子区域探测得到的多个像移量对参考图像与目标图像在滚转、俯仰方向的偏转量进行求解,其原理基于共线方程理论,即不论像平面如何旋转,物点与光学中心连线与焦平面的交点始终为物点在焦平面的像点,如图5所示。
设视场范围内有多个参考物点1~M,在参考图像和目标图像的坐标分别为1(x1,y1)(x1,y1),2(x2,y2)(x2,y2),…,M(rn,rn)(x,y),则由共线方程可知必有一矢量使得下式成立[9]
×0 (4)
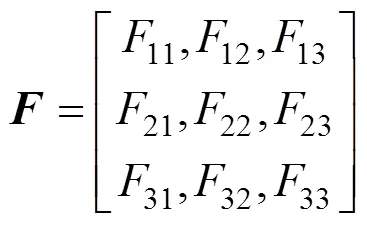
由矩阵理论可知,需要选取至少8个控制点来获取基础矩阵的唯一解。针对8个控制点模型进行方法设计,其中8个控制点即为上所述子区域的中心点,利用联合变换相关的方法对子区域像移量进行探测即可得到控制点在参考图像与目标图像上的坐标。
在获得基础矩阵的唯一解后,可利用Louguet-Higgins[15]提出的本质矩阵对光轴微振动进行求解,其与基础矩阵的关系为
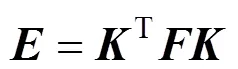
式中为相机的内方位参数(实验室测定),则在、已知后可以在相差一个比例因子的情况下确定本质矩阵。将本质矩阵进行奇异值分解[16]可得=T。
设参考图像与目标图像在微振动下的姿态旋转矩阵为
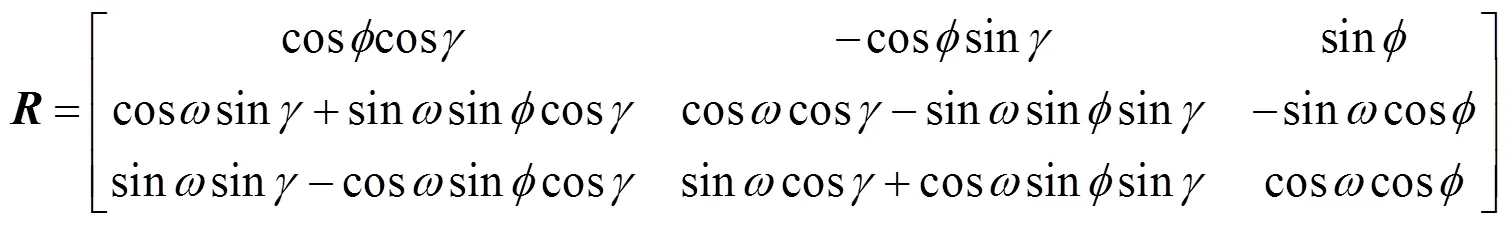
式中为滚转方向偏转量;为俯仰方向偏转量;为偏航方向偏转量(无平动情况下默认为0)。
由Hartley所提出的姿态解算方法[17]可得
≈T(7)
2 微振动探测方法试验验证
静止轨道光谱仪其积分时间一般大于10ms,若要在一次积分时间内对光轴微振动进行准确探测,则小面阵探测器积分时间需为遥感器积分时间的十分之一,即采样频率大于100Hz。微振动探测方法对遥感器俯仰、滚转方向微振动的探测精度需达到1~10μrad,且需要保证探测误差导致的星下点像移小于一个像元。
利用某静止轨道高光谱遥感器参数进行分析后,设定小面阵探测器地面分辨率为25m、焦距为21m、像元尺寸为15μm、探测器尺寸为500像元×500像元。
2.1 仿真方案
设小面阵探测器在相邻两次成像时在俯仰、滚转方向分别存在由微振动所导致的模值为1μrad、6μrad、10μrad的标准偏转量,通过一幅地面分辨率为25m的遥感图像利用摄影测量方法进行仿真,最终得到36组测试数据,每组测试数据包含的两幅图像分别为在不同标准偏转量下相邻两时刻采样得到的遥感图像。
利用上述子区域像移探测与微振动姿态解算方法相结合的微振动探测方法对得到的36组测试数据进行计算,求解得到每组测试数据中两幅遥感图像间的试验偏转量。
2.2 仿真及分析
Tab.1 Test data error along pitching direction μrad

Tab.2 Test data error along rolling direction μrad
(1)光轴微振动方向对探测误差影响
以俯仰、滚转方向标准偏转量模值为6μrad的点为例进行分析(1μrad、10μrad点情况基本相同)。图6为对应点的测量误差值。表3为对应点在星下点位置像移测量误差的均值和均方根误差。
表3 光轴微振动误差均值、均方根误差

Tab.3 Mean and standard deviation of optical axis micro vibration error
由图6、表3可知,随着光轴沿俯仰、滚转方向偏转方向的不同,测试点并未产生粗大误差。通过均方根误差可知全部测试点都处于一个较小的误差波动范围内,因此可认为光轴微振动方向对探测误差没有影响。
(2)标准偏转量幅值对探测误差影响分析
标准偏转量幅值对探测误差影响分析如图7、图8所示。
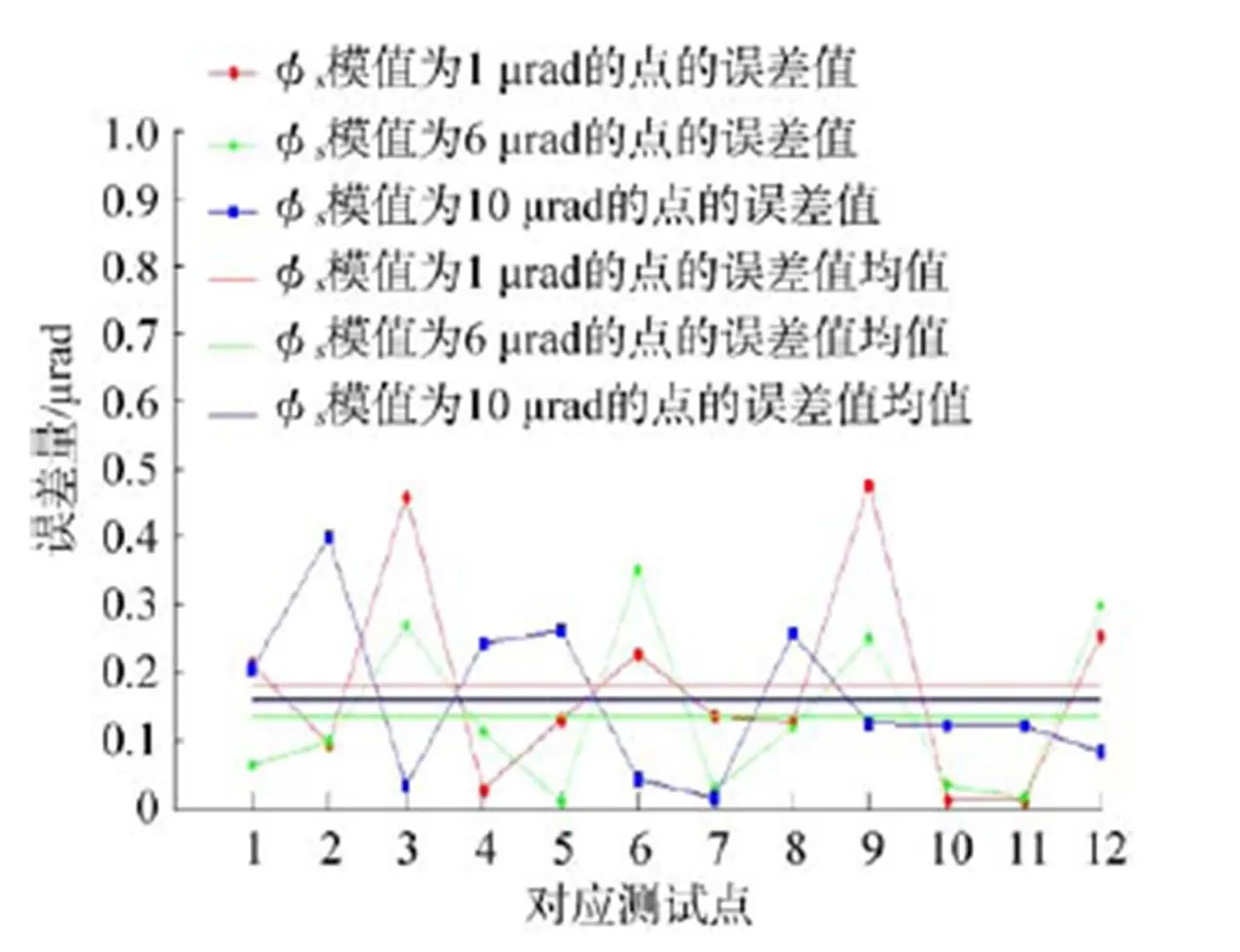
图7 光轴微振动量大小沿俯仰方向误差比较
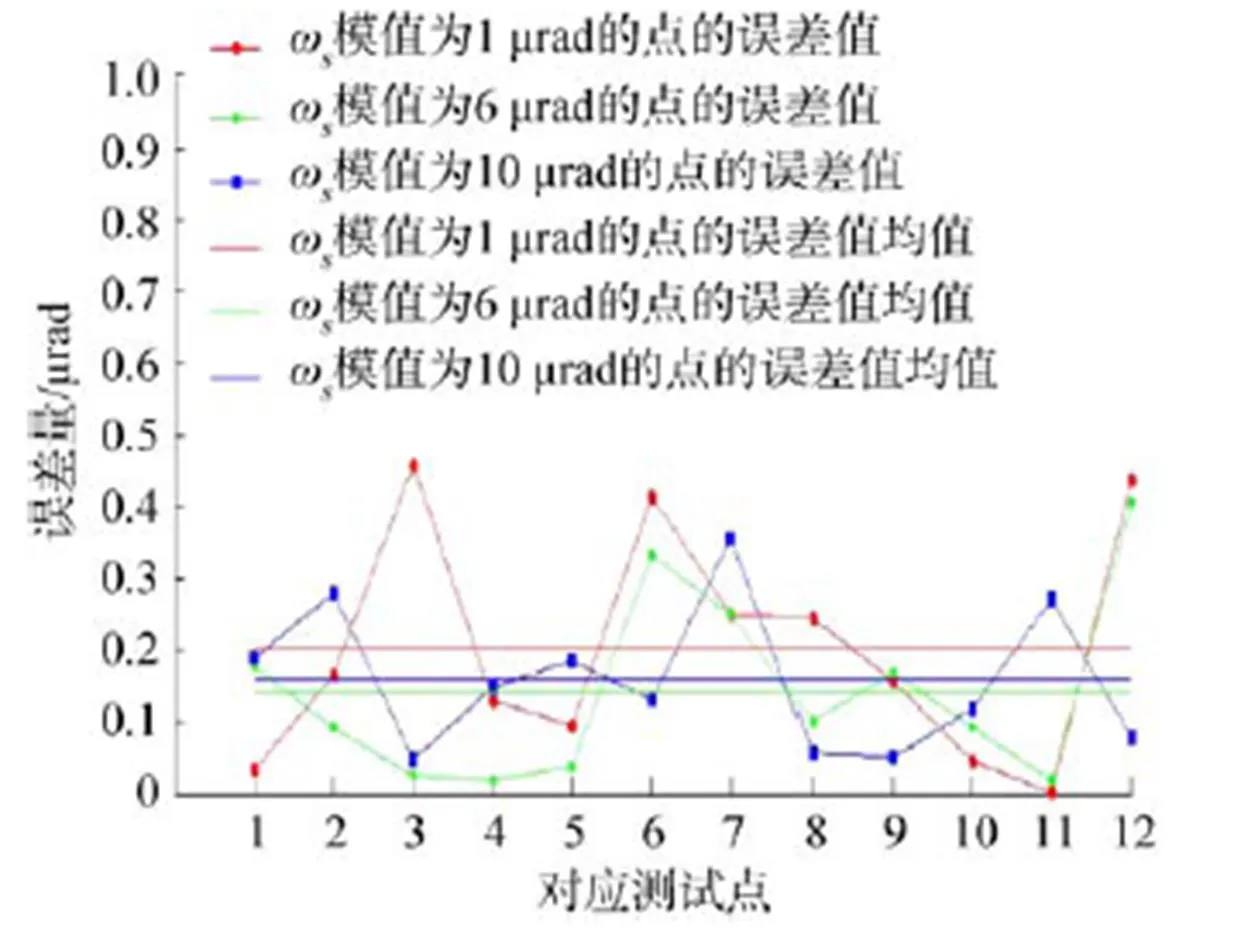
图8 光轴微振动量大小沿滚转方向误差比较
由图7、图8可知,当俯仰、滚转偏转量模值增大时,偏转量误差的均值并无较大变化,由此可知偏转量幅值增大并不会对探测误差产生影响。
(3)总误差分析
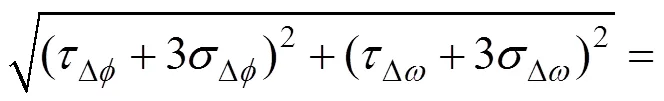
表4 总误差分析

Tab.4 Total error analysis
3 结束语
基于静止轨道光谱仪积分时间长的特点,本文提出了一种将像移探测与微振动姿态解算相结合的探测方法,由试验仿真分析可知,本方法可以有效地对静止轨道光谱仪存在的光轴沿滚转、俯仰方向1~10μrad的高频微振动进行探测,且探测精度不受微振动量大小、方向影响,可有效地应用于遥感器在轨稳像、地面重构等领域。
[1] 陶小平. 地球静止轨道凝视成像系统分时积分稳像技术验证[J]. 光学学报, 2014, 34(13): 143-149. TAO Xiaoping. Technology of Vibration Suppression Based on Multiple Integration for Staring Imaging System in GEO Orbit[J]. Acta Optica Sinica, 2014, 34(13): 143-149. (in Chinese)
[2] 张丽, 汤恩生, 许敬旺. 空间相机像移补偿方法研究[J]. 航天返回与遥感, 2007, 28(3): 19-22. ZHANG Li, TANG Ensheng, XU Jingwang. Studies on the Image Motion Compensation Methods of Space Camera[J]. Spacecraft Recovery & Remote Sensing, 2007, 28(3): 19-22. (in Chinese)
[3] 李浩洋, 刘兆军, 徐彭梅. 浅谈空间光学遥感器稳像技术[J]. 航天返回与遥感, 2010, 31(6): 52-57. LI Haoyang, LIU Zhaojun, XU Pengmei. An Overview on Image Stabilization Method of Space-born Remote Sensing Systems[J]. Spacecraft Recovery & Remote Sensing, 2010, 31(6): 52-57. (in Chinese)
[4] 赵红颖, 金宏, 熊经武. 电子稳像技术概述[J]. 光学精密工程, 2001, 9(4): 353-359. ZHAO Hongying, JIN Hong, XIONG Jingwu. An Introduction to Electronic Image Stabilization Technology[J]. Optics and Precision Engineering, 2001, 9(4): 353-359. (in Chinese)
[5] 林萌萌. 基于惯性测量单元的船用星敏感器定位/姿态方法研究[D]. 哈尔滨工业大学, 2014. LIN Mengmeng. Research on Positioning/Attitude Algorithm of Star Sensor for Ship Basing on Ineritial Measurement Unit[D]. Harbin Engineering University, 2014. (in Chinese)
[6] 安文吉. 某三轴稳定卫星姿态确定及控制系统研究[D]. 哈尔滨工业大学, 2007. AN Wenji. Attitude Determination and Control System of A Three-axis Stabilized Satellite[D]. Harbin Engineering University, 2007. (in Chinese)
[7] 葛任伟, 吴清文, 王运, 等. 基于联合变换相关器的像移测量方法研究[J]. 计算机仿真, 2010, 27(3): 215-219. GE Renwei, WU Wenqing, WANG Yun. The Study of Image Motion Measurement Based on Joint Transform Correlator[J]. Computer Simulation, 2010, 27(3): 215-219. (in Chinese)
[8] 许博谦, 郭永飞, 王刚. 测量空间相机像移量的联合变换相关器的改进[J]. 光学精密工程, 2014, 22(6): 1418-1423. XU Boqian, GUO Yongfei, WANG Gang. Improvement of Joint Transform Correlator for Measurement of Space Camera Image Motion[J]. Optics and Precision Engineering, 2014, 22(6): 1418-1423. (in Chinese)
[9] 徐巧玉. 大型装备在线三维视觉测量系统关键技术研究[D]. 哈尔滨工业大学, 2007. XU Qiaoyu. Study of the Key Technologies of Online 3D Vision Measurement System for Large-scale Equipments[D]. Harbin Engineering University, 2007. (in Chinese)
[10] 满益云, 陈世平. 一种实时测量卫星运动像移的新方法[J]. 航天返回与遥感, 2003, 24(3): 24-29. MAN Yiyun, CHEN Shiping. An Innovative Method for the Real Time Measurements of Image Shift Due to the Motion of the Satellite[J]. Spacecraft Recovery & Remote Sensing, 2003, 24(3): 24-29. (in Chinese)
[11] JANSCHEK K, BOGE T, DYBLENKO S, et al. Image Based Attitude Determination Using an Optical Correlator[C]// Spacecraft Guidance, Navigation and Control Systems, 2000.
[12] TCHERNYKH V, DYBLENKO S V, JANSCHEK K, et al. Optical-correlator-based System for the Real-time Analysis of Image Motion in the Focal Plane of an Earth Observation Camera[J]. Proceedings of SPIE - The International Society for Optical Engineering, 2000, 4113(1): S321-S322.
[13] TCHERNYKH V, HARNISCH B. Compensation of Focal Plane Image Motion Perturbations with Optical Correlator in Feedback Loop[J]. SPIE, Sensors, Systems, and Next-generation Satellite VIII, 2004, 5570: 1-23.
[14] 葛鹏. 基于联合变换光学相关器的图像位移矢量探测技术[D]. 浙江大学, 2012. GE Peng. Image Displacement Measurement Based on Joint Transform Optical Correlator[D]. Zhejiang University, 2012. (in Chinese)
[15] LONGUET-HIGGINS H C. A Computer Algorithm for Reconstructing a Scene from Two Projections[J]. Nature, 1981, 293(5828): 133-135.
[16] 蒋正新, 施国梁. 矩阵理论及其应用[M]. 北京: 北京航空航天大学出版社, 1988. JIANG Zhengxin, SHI Guoliang. Matrix Theor and its Analysis[M]. Beijing: Beihang Univrsity Press, 1988. (in Chinese)
[17] HARTLEY R I. Estimation of Relative Camera Positions for Uncalibrated Cameras[C]//European Conference on Computer Vision. Springer-Verlag, 1992: 579-587.
[18] 李福东. 航空远距离倾斜摄影相机扫描稳像及像移补偿技术研究[D]. 哈尔滨工业大学, 2015. LI Fudong. Research on Scanning & Motion Compensation of Airborne Camera for Long Range Oblique Photography[D]. Harbin Engineering University, 2015. (in Chinese)
[19] 李延伟, 远国勤. 面阵彩色航空遥感相机前向像移补偿机构精度分析[J]. 光学精密工程, 2012, 20(11): 2439-2443. LI Yanwei, YUAN Guoqin. Accuracy Analysis of Forward Image Displacement Compensation Divece for Aerial Scan Color CCD Camera[J]. Optics and Precision Engineering, 2012, 20(11): 2439-2443. (in Chinese)
[20] VELLA F, CASTORINA A, MANCUSO M, et al. Digital Image Stabilization by Adaptive Block Motion Vectors Filtering[J]. IEEE Transactions on Consumer Electronics, 2002, 48(3): 796-801.
[21] MORIMOTO C, CHELLAPPA R. Evaluation of Image Stabilization Algorithms[C]//IEEE International Conference on Acoustics, Speech and Signal Processing. IEEE, 1998: 2789-2792.
(编辑:王丽霞)
A Detection Method for Optical Axis Disturbance of the Remote Sensor
LU Zhijun1,2TANG Shaofan1LI Huan1TIAN Guoliang1
(1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China)(2 Key Laboratory for Advanced Optical Remote Sensing Technology of Beijing, Beijing 100094, China)
Because the hyperspectral remote sensor on stationary orbit has long integration time and many spectral bands, the image quality is greatly influenced by high frequency micro vibration. In order to improve the spatial resolution, the optical axis micro vibration should be detected accurately to guide rectifying the image stabilization system. In view of the detection problem of the optical axis micro vibration, a detection method was firstly proposed, combining image motion detection with micro vibration attitude determination, which can be used to detect the high frequency micro vibration along the pitching and the rolling directions of the optical axis. Secondly, taking the remote sensing image which conforms to the spatial resolution requirements, as the reference image, a series of test images which have the defined optical axial attitude difference with the reference images are established based on photogrammetry. Taking the reference and test images as input, the optical axis attitude difference in the sampling interval is computed by this algorithm. Finally, the simulation results are analyzed. From the simulation results, one can know that the method is effective to detect the high frequency micro vibration of the optical axis below 10mrad.
geostationary orbit; micro vibration; image motion; photogrammetry; hyperspectral; space remote sensing
TP751.2
A
1009-8518(2018)01-0061-08
10.3969/j.issn.1009-8518.2018.01.008
鲁之君,男,1992年生,2015年获南京航空航天大学探测制导与控制专业学士学位,现在中国空间技术研究院飞行器设计专业攻读硕士学位。研究方向为遥感器总体设计。E-mail: luzhijun1992@163.com。
2017-10-13

