基于学习的地震剖面超分辨率重建方法研究

刘旭跃， 黄 骏

(中国石化 石油物探技术研究院，南京 211103)

0 引言

地震剖面图是通过地震施工在地面上布置一条条的测线，沿着这些测线采集地震信息，然后经过计算机处理而得到的图像。经过地质解释的地震剖面图像就如同自地表向下的地层切片，在长度和深度方向上显示了地下的地质构造情况。它具有明显的纹理特征，不同的纹理代表着不同的地质体。影响地震剖面品质的因素有多种：采集环境差产生干扰波、复杂的表层结构影响激发能量的下传、复杂的地下地质条件影响地震波能量的接收、野外施工中高程不准、室内资料处理参数设置不精确等。国内、外学者针对此问题，提出了很多改善的方法，大致分为2类：①从物理学角度，对信号数据本身进行处理(如李晓飞[1]概括的振幅处理，叠前噪音压制、静校正和反褶积等技术)；②从地震采集方法上面改进(如采取加大激发能量、强化激发手段等)措施来获得好的资料，但是大大增加了采集成本。

随着计算机图像处理技术的发展，利用图像超分辨率重建技术能从低分辨率图像中重建高分辨率图像，克服图像获取过程中产生的不利条件，从而获得更好的图像内容，提高场景识别的准确性，达到提高图像分辨率，改善图像质量的目的[2]，以实现在成本相对较低的条件下获得更高分辨率的图像[3]。

笔者首先采用优化的TV去噪技术，去除地震资料噪声，提高地震资料的信噪比，然后采用逐层相似性学习的方法进一步提高地震剖面图像分辨率。这样得到的高质量剖面图，有助于解释人员更好地将地震信息转化成地质信息，以达到精确重现地下地质的情况，从而对测区作出更合理的油气评价。

1 相关理论

1.1 TV模型图像去噪

图像去噪的目的是去除原有图像存在的噪声，同时又要保留图像的细节结构(如边缘、纹理等)。TV模型不但能去除图像中原有的加性噪声，而且能有效地保留图像的边缘信息。在日常生活中，灰度图像对应着一个矩阵，矩阵的位置对应着图像的像素点，矩阵中的元素值对应着图像像素点的灰度值，因此需要对模型离散化，离散化后的TV 模型为[4]：

minG(Au)+H(u)

(1)

其中:u∈Rm,u为图像按列拉成的列向量；A∈Rn×m为差分算子，都是凸函数；G:Rn→(-∞，∞]；H:Rm→(-∞，∞]都是凸函数，由于G和H所取的范数不同，我们考虑如下的模型。

L1-ATVH(u)=‖u-f‖1

G(Au)=‖Au‖1

(2)

G(Au)=‖Au‖1

(3)

L1-ITVH(u)= ‖u-f‖1

(4)

(5)

设X为N×N的矩阵，x为X的列向量拉成的向量，则

Xi,j=xi+(j-1)NI,j=1,2,…,N

(6)

设D为N×N矩阵

(7)

为一阶差分矩阵。

则A为一个2N2×N2的矩阵

(8)

混合积的性质为

(A⊗B)(C⊗D)=(AC)⊗(BD)

(9)

(A⊗B)T=AT⊗BT

(10)

(A⊗B)-1=A-1⊗B-1

(11)

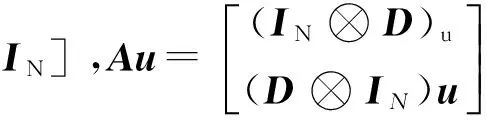
(12)

(13)

(14)

1.2 超分辨率图像重建

超分辨率即通过硬件或软件的方法提高原有图像的分辨率，通过一系列低分辨率的图像，来得到一幅高分辨率的图像过程就是超分辨率重建。高分辨率意味着图像中的像素密度更高，能够提供更多的细节，而这些细节在许多实际应用中不可或缺。根据输入图像的多少可以将超分辨率重建问题分为2类：多图像、单图像[5]。①多图像超分辨率是指把一系列图像(或视频的一部分)用于重建，它们都包含着高度相关的信息(即相对场景运动)[6]；②单幅图像超分辨率重建技术通过放大图像的同时增强细节来提高图像分辨率，适用于无法获取同一场景图像序列的各种情况[7](如古代文物资料修复，高速运动物体的瞬时成像、无法重现或连续拍摄的医学图像处理等)。笔者是采用单幅图像超分辨率重建。

单幅图像超分辨率算法根据获取的目的分为3类：①基于插值的方法；②基于重建的方法；③基于学习的方法。

基于学习的图像超分辨率算法最早由卡耐基-梅隆实验室的Baker S[15]在2000年提出的。利用贝叶斯学习框架，对一个低分辨率图像集进行训练，产生一个学习模型，通过这个模型预测图像高频细节信息。目前常用的学习算法有Freeman等[8]提出的Example-based方法、Chang等[9]提出的基于邻域嵌入的方法、Karl等[10]提出的使用支持向量机的方法等，我采用的方法是在局部相似性学习的基础上进行改进。

为了能将重建图像中的有用信息通过某种方式组合起来，集成一幅高质量的图像[6]，需要选择合适的训练集和邻域集进行学习。根据图像的局部相关性特点，假定训练集和邻域集都来自一个分布模型。其数学模型如图1所示。

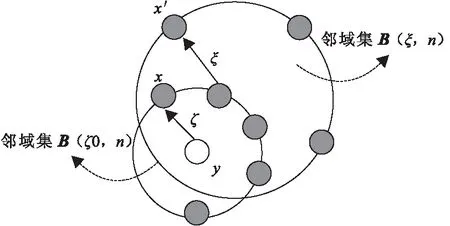
图1 数学模型Fig.1 Mathematical model

邻域集是由待估计像素y和其最近邻像素集合B(ξ，n)，B(ξ，n)={x∈Ω,||y-x||≤ξ}，其中ξ=[ξ0，ξ1，……，ξn]是距离向量，ξi表示中间像素和其邻域像素点的距离。N是邻域集的像素数量，以Ω代表已知像素集。

根据邻域集的像素，我们可以使用式(15)来求取y，

y=βTX

(15)

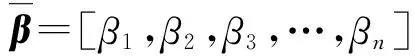
训练集在待估计像素y邻近选择其中一个训练窗口B(ξ，n)，其中ξ=[ξ0，ξ1，…，ξn]是与ξ成比例的距离向量，即ξ=ιζ,ι是比例因子，且ι≥1。所有的训练子窗口B(ξ，n)形成训练集。

在每一个训练窗口中，中心像素点和其周围像素点的距离正比于邻域窗口内中心像素点和其周围像素点的距离。

局部几何性指的是，在一个集合中，邻域像素点对中心像素点的贡献度。邻域窗口与训练窗中的贡献度的对应关系，称为局部几何相似性。系数β代表了邻域窗口和训练窗口的局部几何结构性，可通过对训练窗口的局部几何性的学习，将训练窗口的此种局部几何性传递至邻域窗口中，即令训练集中所有训练窗口满足统一的数学模型，所有的m个训练窗口B(ξ，n)满足式(15)，从而得到优化解β的估计值：

(16)

其中

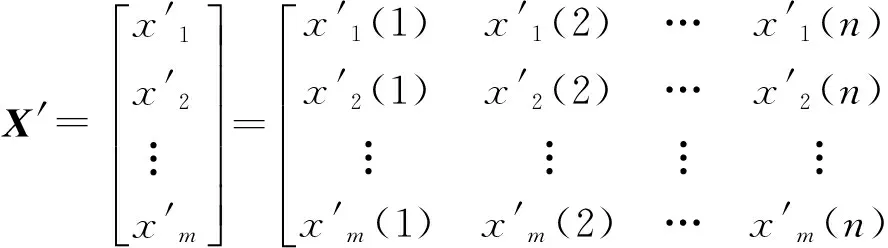
(16)

其中,X′是各训练窗口中的周围像素，是m*n矩阵，每一行代表了每个训练窗口的周围像素，而x则是对应于每个训练窗口的中心像素。

我们可以通过最小二乘式(18)求解式(17)。

β=(x′Tx′)-1(x′Tx)

(18)

2 地震剖面超分辨率重建技术流程

由于地震剖面图是由检测出来的信号生成的，每个点是代表地震震动的强度，不同于普通的灰度图像。针对地震剖面特点，总的技术流程框架如图2所示。

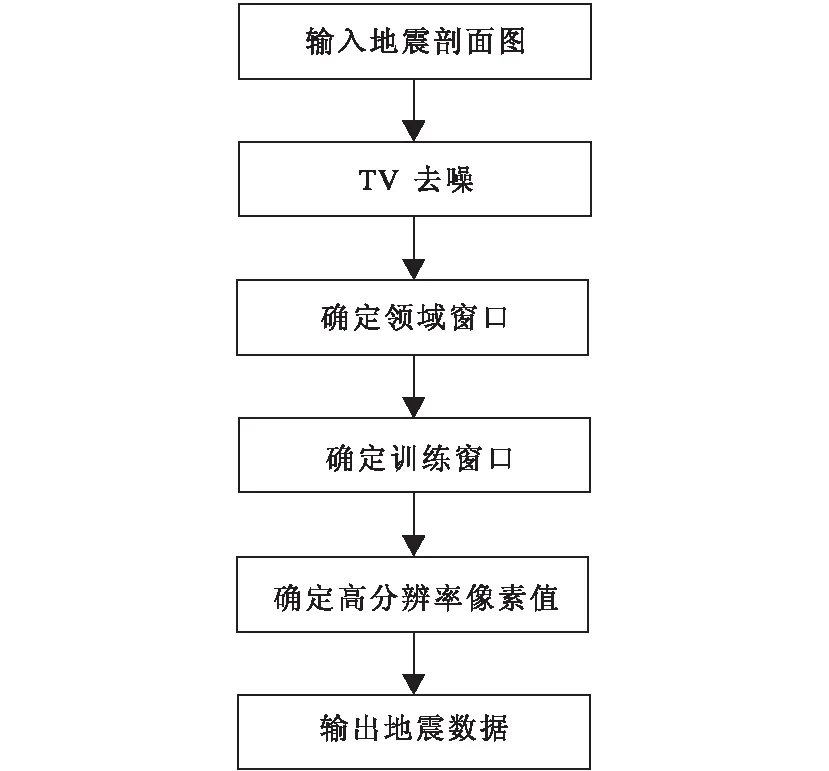
图2 总的技术流程框架Fig.2 General technical process framework

2.1 TV去噪算法

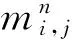
(19)

(20)

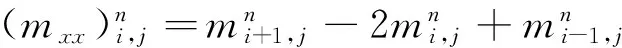
(21)

(22)

(23)

离散迭代格式为：

(24)

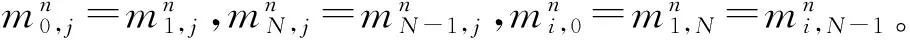
2.2 逐层相似性学习算法

建立数学模型，对于待求区域中的像素点y,认为此点的值是来自于其领域像素值的加权平均，即

y=βX

(25)

其中：权值β为i*1列向量；X∈B(ε,i),也为i*1列向量；B(ε,i)为邻域窗口，ε为邻域半径，i为此邻域窗口中的像素数目。

围绕未知点选择训练集B(ε,j)，它是一个更大范围的邻域窗口，对此集合中的每一个像素点形成对应于未知像素点的训练窗口，假定每个训练窗口中像素点及其周围邻域都满足公式(24)，则权系数可以通过求取MSE极小得到。

(25)

式中：X∈B(ε,j)。

待处理的图像点定义邻域窗口时，其所包含的像素中经常会存在未知点，此时对应的训练窗口中包含的点应与邻域窗口存在着方向上一一对应的关系。此模型所具有的边缘导向属性是从其训练窗口的各个子模式所拷贝学习得来的。为保持边缘特征，通过加权的方式来选取，则式(24)变为：

(26)

其中：Q为n*1阶向量。

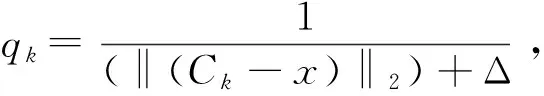
然后填补未知点顺序。为在取得有用信息和误差传递方面去一个平衡点，采用逐层递进的分组行进法。该方法是找到满足

|▽T|F=1到达的时间的一组数据，

(27)

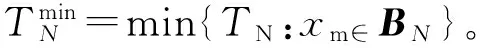
逐层递进的分组行进法的一组数据对应于修补边界层，对此数据同时进行更新，每层数据的更新只受上层数据或已知数据的影响，与本层已求出的数值无关。

3 实例与分析

3.1 实例比较

本方法采用塔河实际资料为例进行测试，选用测线范围在450条～1 100条，CDP范围450道～1 500 道，并选用峰值信噪比(PSNR)和结构相似度(SSIM)，作为标准来客观评价重建图像的质量。测试和训练都采用某原始地震剖面图，如图3所示。经过TV方法处理，λ=1.0时得到的地震剖面图如图4，然后经逐层相似性学习处理后得到地震剖面图如图5。

把图4和图5的地震剖面放大效果进行比较，如图6、图7所示。

3.2 效果分析

采用峰值信噪比(PSNR)、边缘保持指数(EPI)和结构相似性(SSIM)进行评价。PSNR用来衡量滤波器的去噪能力，值越大则图像质量越好[11]；EPI衡量边缘保持能力，EPI值越大，边缘保持能力越强；SSIM衡量两张图像的结构相似性，范围从-1到1，值越大越相似。

图3 原始地震剖面图Fig.3 Original seismic profile

图4 TV方法处理后的地震剖面图Fig.4 Seismic profile after TV method

图5 逐层相似性学习处理的地震剖面图Fig.5 Seismic profile of layer by layer similarity learning processing

图6 局部放大剖面图(TV方法)Fig.6 Local magnification profile (TV method)

图7 局部放大剖面图(逐层相似性学习)Fig.7 Local magnification profile (layer by layer similarity learning)

峰值信噪比：

PSNR=

(28)

EPI：

(29)

SSIM：

SSIM=

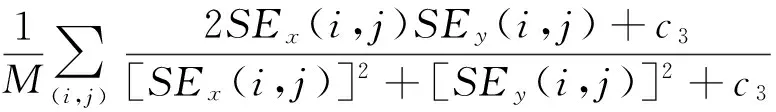
(30)

表1是降噪后的效果值。图4较图3而言地震剖面同相轴连续性更好，层间结构也更清晰。

表1 降噪效果

把经TV方法处理和学习处理的图分别与图2原始地震剖面进行SSIM计算，表2列出两种方法结构相似性比较值。本文方法得到的图与原始图的结构性更相似。

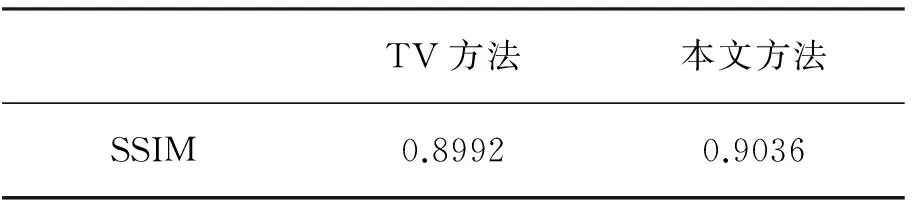
表2 结构相似性比较

4 结论

笔者利用图像处理方法，通过优化的TV全变分算法提高地震剖面的信噪比，较好地保持图像边缘，然后采用逐层相似性学习方法，通过邻域窗口，选取合适的训练窗口，得到待重建的高分辨率值。实现将单幅图像未知区域的自行进行修复。结果分析表明，处理后的图像不仅提高了原始图的分辨率，还能更多、更有效地保留有效信息，方便后期地震解释工作的顺利开展。

[1] 李晓飞.地震高分辨率处理技术[J].青年科学,2014,18(9):212-212. LI X F. Seismic high resolution processing technology[J].Academic research and discussion,2014,18(9):212-212.(In Chinese)

[2] 李展,吴少春,彭青玉.图像自适应分块单幅超分辨率算法[J].系统工程与电子技术,2015,37(10):2411-2417. LI Z, WU S C,PENG Q Y. Image adaptive block single super-resolution algorithm[J]. System engineering and electronic technology,2015,37(10):2411-2417. (In Chinese)

[3] 杨帅锋,赵瑞珍. 基于低秩序矩阵和字典学习的图像超分辨率重建[J].计算机研究与发展,2016,53(4):884-891. YANG S F,ZHAO R Z. Image super resolution reconstruction based on low order matrix and dictionary learning[J]. Computer research and development,2016,53(4):884-891. (In Chinese)

[4] 邓淑龙.TV模型图像去噪的算法分析[D].浙江：浙江大学,2014. DENG S L. Analysis of image denoising algorithm based on TV model[D]. Zhejiang: Zhejiang University,2014. (In Chinese)

[5] 李欣,崔子冠,朱秀昌.超分辨率重建算法综述[J].电视技术,2016,40(9)：1-9. LI X,CUI Z G,ZHU X C. Overview of super-resolution reconstruction algorithms[J]. TV Technology,2016,40(9)：1-9. (In Chinese)

[6] PARK S C,PARK M K,KANG M G.Super-resolution image reconstruction:a technical overview[J].IEEE signal processing magazine,pecial issue of super-esolution image reconstruction,2003,20(3):21-36.

[7] 曾宪华,候苏丽.基于宽度学习的集成超分辨率重建方法[J].计算机工程与设计,2016,37(9):2526-2529. ZENG X H,HOU S L. Integrated super-resolution reconstruction method based on width learning[J]. Computer engineering and design,2016,37(9):2526-2529. (In Chinese)

[8] MORSE, B., SCHWARTZWALD, D.Image magnification using level-set reconstruction[C].Proc. IEEE International Conf. Computer Vision,2001:333-341.

[9] LIU,C.,SHUM, H.Y., ZHANG, C.S.Two-step approach to hallucinating faces: global parametric model and local nonparametric model[J].In:Proc. IEEE Conf. on Computer Vision and Pattern Recognition， 2001：192-198.

[10]BAKER, S., KANADE, T.. Limits on super-resolution and how to break them[J].IEEE Trans.Pattern Anal. Mach. Intell，2002(24)：1167-1183.

[11]刘博.结构相似性图像质量评价方法研究[D].辽宁：大连理工大学,2012. LIU B. Research on image quality evaluation of structural similarity[D]. Liaoning: Dalian University of Technology,2012. (In Chinese)

[12]公成敏. 全变分原理在地震数据去噪中的应用[J].计算机与数字工程,2014,297(42):1271-1274. GONG C M. The variational principle and its application in denoising of seismic data[J]. Computer and digital engineering, 2014,297(42):1271-1274. (In Chinese)

[13]张文娟,王艳红.边缘结构相似性图像质量的高阶统计及评价[J].西安工业大学学报,2016,36(3):173-176. ZHANG W J,WANG Y H. High order statistics and evaluation of edge structure similarity image quality[J]. Journal of Xi'an Technological University,2016,36(3):173-176. (In Chinese)

[14]杨芳.基于学习的图像超分辨率技术及其应用研究[D].北京：北京理工大学,2011. YANG F. Research on image super resolution technology based on learning and its application[D].beijing: Beijing Institute of Technology,2011. (In Chinese)

[15]BAKER S, KANADE T. Limits on Super-resolution and How to Break Them[J]. Computer Vision and Pattern Recognition, 2000, 9(2): 372-379.