4种分类算法参数选择及分类特点研究
王正杰,杨伟丽,王 喆,侯玉珊,郭银景
(山东科技大学电子通信与物理学院,山东 青岛 266590)
0 引 言
分类算法是人工智能、模式识别和数据挖掘领域中重要的数据处理方法,其目的是通过样本数据建立分类模型或函数,将实体属性值分类到给定的数据类别中,常用的分类算法可以分为参数化模型和非参数化模型[1]。当使用参数化模型时,需要通过训练数据估计参数,然后对数据进行分类操作,典型的包括感知机、逻辑斯谛回归和线性支持向量机。非参数化模型无法通过一组固定参数进行表征,而且参数数量也会随着训练数据增加而递增,典型的包括决策树(含随机森林)、采用核函数的支持向量机和K近邻。进行数据分类时,数据特征空间维数、数据噪声以及分类算法参数设置都会影响分类精度[2]。同时,算法的参数选择在实际应用中也有很广泛的需求[3-4],对算法参数寻优是算法应用的重要基础[5-6]。本文选择2类模型中的代表算法,通过建立不同类型数据集并设置不同算法参数,分析多种算法分类效果,对了解不同算法分类精度及适用数据类型具有重要的指导意义。
1 算法基本原理
1.1 KNN
KNN是最近邻法的推广,KNN算法通过搜索模式空间,找出待分类样本的k个邻近数据。具体地说,对未知(待分类)样本xt分类时,在训练样本集中寻找与待分类样本xt距离最近的k个样本,若这k个样本大多数属于某一类别,则判定该测试样本属于该类[7]。因此,KNN算法的2个重要因素是距离最近的样本数k和“距离”度量公式。
假设有C个类别:w1,w2,…,wc,若k个近邻样本中属于w1,w2,…,wc类的样本数分别是k1,k2,…,kc,此时决策规则为:
则xt∈ωi,即未知样本被分配到k个近邻中样本数最多的那一类中。
常用的距离度量公式如下[8]:
3)切比雪夫距离:max|xi-yi|(i=1,2,…,n);
4)闵可夫斯基距离:
其中 s-1为样本协方差矩阵的逆矩阵。
1.2 支持向量机
SVM是一种在线性可分条件下求最佳分类超平面基础上发展而来的算法,其主要思想是将低维线性不可分问题通过核函数映射到高维特征空间,变成高维空间线性可分问题,在线性可分条件下求最优分类面[9]。
设训练样本x1,x2,…,xn,x∈Rm,训练样本所属类别(分类标签集)为y∈{+1,-1},传递函数(分类规则)定义为:
f(x)=sgn (wTx+b)
将求解最优分类面问题表示为如下约束问题[10]:
(1)
st. yi(wTxi+b)≥1 (i=1,2,…,n)
(2)
考虑到存在噪声引起的离群点,在最优化目标中加入惩罚系数和松弛变量,即增加对应样本xi允许偏离函数间隔。约束条件(2)式就变成:
yi(wTxi+b)≥1-ξi, i=1,2,…,n
(3)
优化目标式(1)变成:
(4)
其中,C为惩罚因子,ξ为松弛变量,该值可自行设定。
通过拉格朗日乘子法,引入辅助变量λi,可以得到分类函数:

其中,xi为第i个样本向量,x为未知向量,〈xi,x〉表示2向量的内积。
从上式可以看出,若选择不同的内积计算方法,则可以得到不同的分类函数,常使用的核函数有如下形式[11-12]:
1)高斯核函数:
K(xi,x)=exp (-‖xi-x‖2/2σ2)
2)多项式核函数:
K(xi,x)=((xi·x)+1)d, d=1,2,…
3)感知器核函数:
K(xi,x)=tanh [β(xi,x)+b]
4)高斯径向基核函数(RBF):
K(xi,x)=exp (-γ‖xi-x‖2)
5)线性核函数:
K(xi,x)=〈xi,x〉
1.3 决策树——CART算法
决策树是基于训练数据集的特征,通过一系列的问题来推断样本所属类别的一种方法[13]。CART算法可对特征属性进行二元分裂,分裂之后得到2个子样本,则每个内部结点都有2个分支。无论一个属性有几个取值,决策树的每一步决策只能是“是”或“否”,即分支系数始终为2。
设x1,x2,…,xn代表单个样本的n个样本属性,y代表所属类别。CART算法通过多次分裂将n维空间分割成不重叠的矩形。
分裂步骤如下:
1)选取xi,再选取xi的一个值vi,n维空间被vi划分为2部分。一部分满足xi≤vi,另一部分都满足xi≥vi;
2)对1)得到的2部分重新选择属性,按照1)继续划分,直到将整个n维空间被划分完。
为使划分效果更好,CART采用了一种称为“节点不纯度”的指标来度量进行二元分裂时的不纯度。常用的几种“不纯度”测量函数是[14-15]:
1)Gini指标(随机选中的样本被误分时的误差率)。
假设有C种类别,则节点s的Gini不纯度为:
其中,pi是节点s中属于类别i的概率,Gini(s)=0时,所有样本属于同类。Gini指数越大,样本包含的类别越多。
2)方差不纯度:
I(s)=p(w1)p(w2)
该不纯度适用于二分类问题。
3)“熵不纯度”(Entropy Impurity):
2 主要参数及作用
2.1 KNN
对于KNN分类模型,需要对近邻数k和距离度量公式这2个参数进行选择。
1)k值的设定。值大小会影响KNN模型的复杂度。k值过小会降低分类的精度,增大模型复杂度,但过于复杂或过于简单的模型的复杂度的测试准确率也比较低;k值过大且测试样本属于样本数量较少的类,反而会增加数据的含噪度,降低分类精度。

2)距离度量的选择。闵氏距离是常用的距离计算方法,当p=2时为欧氏距离,而马氏距离由于能够利用样本协方差获得统计特性,因此在计算样本距离上有很大的优越性,这里选择这2种距离公式进行分析。
2.2 SVM
对于支持向量机核函数本文选择线性核函数和径向基核函数,即Linear SVM和RBF SVM,支持向量机的参数选择和比较是该算法的重要研究内容[16-17]。这里主要设定惩罚系数C和RBF核函数的系数γ这2个参数。
1)惩罚系数C,即松弛变量的系数。
主要作用:在优化函数里平衡模型复杂度和训练错误率这两者之间的关系,控制着对误分样本的惩罚程度。若C取值比较小时,意味放弃离群点,即选择少量样本作为支持向量,支持向量和超平面的模型也会变得简单,训练误差较大,导致“欠学习”。该值较大时,对经验误差的惩罚大,代表保留距离较远的离群点,即选择较多样本作为支持向量,则支持向量与超平面的模型变复杂,使“过拟合”出现的可能性增加。在Scikit-learn中,C默认值是1。
2)RBF核函数的系数γ。
RBF核函数:
k(xi,x)=exp (-γ‖xi-x‖2)
其中γ指某个样本对整个分类超平面的影响。
γ值的大小代表单个样本对整个分类超平面的影响程度。当γ比较小时,影响比较大,易被选为支持向量;当γ比较大时,影响比较小,不易被选为支持向量。Scikit-learn中γ的默认值是1/样本特征数。
当同时考虑C和γ时,若C比较大且γ比较小,则支持向量较多,模型会比较复杂,容易“过拟合”;若C比较小且γ比较大,则模型简单,支持向量少。
2.3 决策树
对于CART算法,需要设定的主要参数为决策树的最大深度及“节点不纯度”指标。决策树最大深度当数据样本少或者特征属性比较少的时候该值可被忽略。若模型样本数量和特征比较多的情况下,需要限制决策树的深度,并根据数据的分布决定该取值。常用的可以取值10~100之间。“节点不纯度”指标使用Gini和Entropy不纯度。
3 实验仿真
本文选用Pycharm编程环境,使用Scikit-learn模块进行实验分析。首先分析不同参数下分类算法的最优参数,根据所选最优参数分析不同噪声下分类算法的分类效果。
3.1 数据集
这里选择2种数据集,用make_moons函数生成的数据集1和make_circles函数生成的数据集2。根据分类的效果,在讨论最佳参数时,采用数据集1,在进行更详细的讨论时,使用2组数据集。首先使用数据集1的3组不同噪声下的数据作为分类算法在不同参数下的精度数据,类别标记个数为2,加入的数据噪声分别是0.1,0.3和0.5,将100个样本分为40个训练样本和60个测试样本。
3.2 参数分析
通过仿真得出分类算法主要参数下的分类精度结果见图1~图5。
1)对于KNN算法,通过分析图1得出如下结论:
①2种距离度量具有相似特性,即当噪音取3种不同值时,分类精度曲线可以大致分成对应3组,这表明噪音对不同距离度量有相似影响。
②当同一噪声下,选用闵可夫斯基距离得到分类精度较高于马氏距离得到分类精度。
③选择同一种度量距离时,数据噪声变大,分类精度降低。

⑤k值过小或过大都会影响分类精度,因此在比较分类算法分类效果时,根据经验规则和上述参数分析结果,令KNN算法的近邻值k=6。

图1 不同噪声及不同k值下KNN算法精确度

图2 不同噪声及最大深度下决策树分类精确度

图3 不同系数RBF核函数分类精确度(n=0.1)

图4 不同系数RBF核函数分类精确度(n=0.3)

图5 不同系数RBF核函数分类精确度(n=0.5)
2)对于决策树算法,通过分析图2得出如下结论:
①2种不纯度指标具有相似特性,随着深度变化,分类精度有所不同,但分类精度增加或者减少趋势一致。
②当数据噪音为0.1和0.3时,2种指标的4条曲线可以分为一组,定位精度较高;当数据噪声为0.5时,2种指标的曲线可以分为一组,该算法对数据分类效果急剧下降,因此该算法处理含有噪声较大数据能力较弱。
③同一种噪声下,决策树分类精度随着最大深度(2~20)增大而变化;当噪声较小时,分类精度随着深度增加而增加,当噪声较大时,分类精度降低。
④对于2种“节点不纯度”指标,数据噪声相同时,选用“Gini”指标时精确度高于选用“Entropy”指标时精确度。
⑤在比较不同分类算法分类效果时,令决策树节点度量指标为“Gini”。为使在不同噪声情况下分类精度都可以取到较高的分类精度,选取最大深度值为6。
3)对图3~图5分析,同一种噪声数据下,惩罚系数C和RBF核函数系数改变都对精确度有着不可忽略的影响。RBF系数γ的取值一般为1/样本特征数,因选用样本特征数为2,此处γ=0.5。为研究参数对分类精度的影响,令RBF系数取值范围为0.1~1.0。惩罚系数C取值范围为0.5~1.5。
对RBF SVM算法,通过分析图3~图5得出如下结论:
①随着噪声增大,分类精度逐渐降低。
②当噪声为0.1时,分类精度随着γ的增大而增大;当噪音为0.3时,分类精度基本不随着γ变化而保持稳定;当噪声达到0.5时,分类精度随着γ的增大而减小。
③当噪音较小时,γ可以适当设置为较大值;当噪音适中时,γ只要不是较小值即可获得较好精度;当噪音较大时,γ应该取较小值。
④当γ=0.5±0.2时,不同种噪声下,都取得良好精度。
⑤当惩罚系数C较大γ较小时或者C较小γ较大时,分类精度都降低。
对于支持向量机核函数为线性核函数时,其主要参数为惩罚系数C,这里根据图3~图5的结果来选择参数大小。
表1 各算法重要参数设置

主要参数选择实验取值KNN(K近邻法)k、距离度量公式k=7、闵可夫斯基距离SVM(支持向量机)C核函数=“linear”C=1核函数=“RBF”系数γγ=0.6,C=1决策树最大深度、不纯度指标max_depth=6,Gini
为了区分不同算法对数据边界分类能力,这里选择各种算法性能最好参数来进行各种算法的综合分析,所选主要参数见表1。
3.3 分类效果分析
根据所选参数,仿真得出算法对2种数据集在不同噪声下分类结果,如图6和图7所示。总体来讲,大部分分类算法的分类精确度都随着噪声增大而降低。2种数据集除了数据集2的RBF SVM算法在噪音为0.1时有最好分类效果外,数据集1在不同噪音条件下,所有算法都有更好分类精度,这说明通常情况下,不同类型数据集在大部分算法上比其它数据集会有更好的分类效果,或者说能否有效分类主要由数据集本身决定。
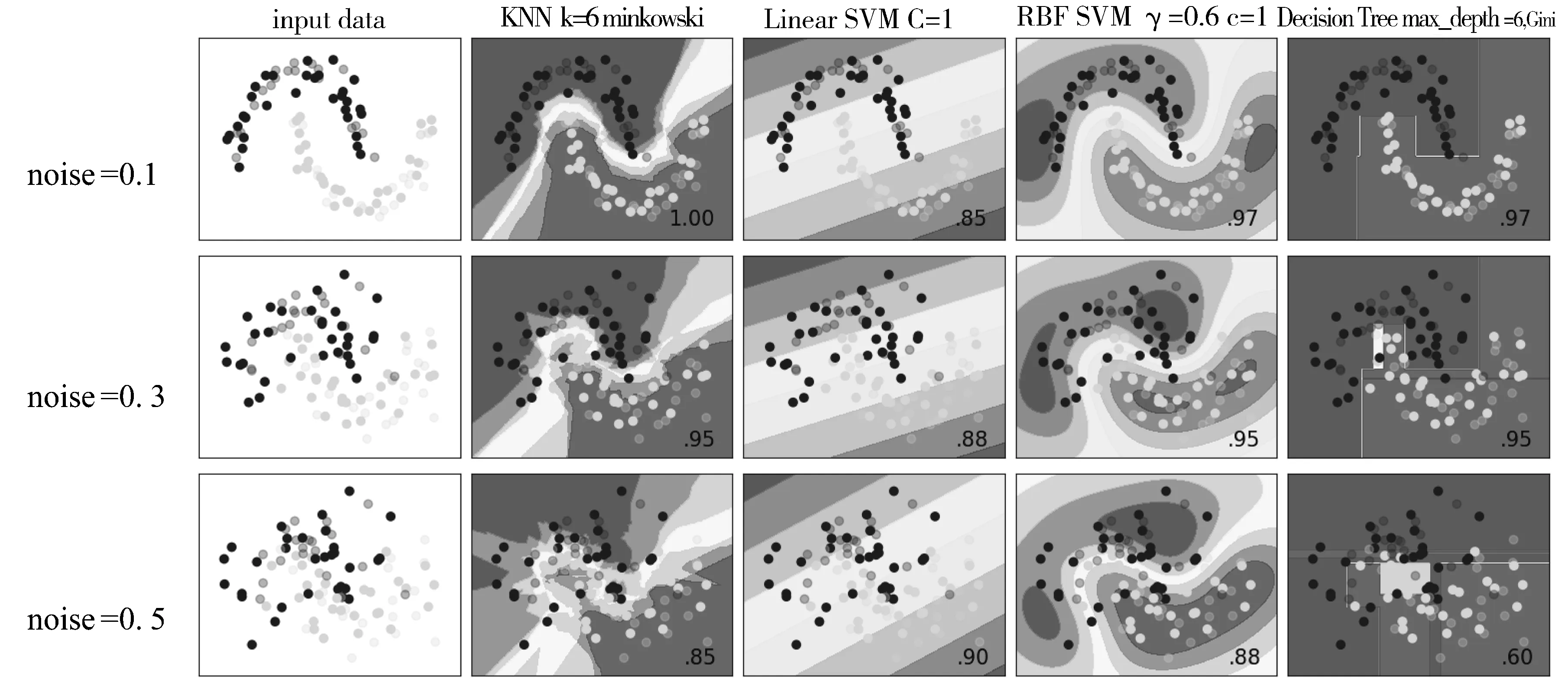
图6 分类算法对make_moons函数产生数据分类结果

图7 分类算法对make_circles函数产生数据分类结果
在数据集1条件下,Linear SVM分类精度随着噪音增加,分类精度反而增加,因为噪音越低,节点分布越密,更不容易获得分类平面。其它算法随着噪音增加分类精度降低,但是不同算法之间变化程度不同,当噪音为0.1和0.3时,3种算法都有95%分类精度,当噪音增加到0.5时,KNN和RBF SVM拥有85%以上分类精度,而决策树由于只能设置直线分类边界导致其精度下降为60%。当噪音较小时,Linear SVM分类精度比其他3种方法都低,当噪音达到0.5时,该方法分类精度反而超过其他3种方法,这表明,不同的算法对噪音的适应能力不同,在给定数据集的情况下,若已知噪音程度,可以选择有效分类方法提高分类精度。在本数据集情况下,RBF SVM基本上拥有最好分类能力。
在数据集2条件下,Linear SVM分类精度没有随着噪音增加而发生变化,其他3种算法分类精度都随着噪音增加急剧下降。当噪音较小时,3种算法都有很高分类精度,当噪音增加时,KNN和RBF SVM分类精度从100%降至75%,决策树降为65%,而KNN在噪音为0.5时,分类精度仅为45%,这表明在给定数据集情况下,不同算法分类精度有很大差别。在本数据集情况下,RBF SVM拥有最好分类能力。
对于2种数据集,KNN和RBF SVM在不同噪音下都有类似的分类精度,这主要由于两者都使用距离来判断节点类别,并且可以形成曲线边界,因此两者在所给数据集和不同噪音参数下,分类精度大部分情况下比较接近,都有比较好的分类能力。而线性支持向量机和决策树都只能采用直线作为分类边界,当噪声变大时,分类效果明显变差,因此,曲线分类边界明显比直线边界拥有更好的分类能力。在数据集1的情况下,数据有明显界限,虽然当噪音增加时,边界不太清晰,但是3种算法除了决策树,都能达到85%准确率。在数据集2情况下,数据点没有线性边界,因此,当噪音增加至0.5时,数据点之间边界已经非常模糊,除了RBF SVM可以绘制任意曲线边界的分类方法能达到65%分类精度,其他分类方法分类精度已经降至50%及以下。总体上来说,基于RBF SVM在各种条件下,拥有较好的分类精度。
3.4 分类精度及时间消耗分析
计算时间运行环境为:Windows10专业版64位、Intel i5-6500CPU(3.2 GHz)、8 G DDR4内存、固态硬盘。本文以n=0.3为例,分析当节点数为100、1000、5000、1万和10万时的分类精度和运行50次的平均时间消耗对算法性能做分析。因为当节点数少于1000时,分类算法在时间上没有明显的区别,这里以节点数为1000的运行时间作为基准,如表2所示进行分析。
从表2可以看出,KNN所需时间最少,决策树次之,支持向量机花费时间最多。从图8和图9可以看出,2种数据集都表现出如下相同的规律,当节点数在1万以内,单位节点消耗时间迅速增加,当节点数量继续变多时,消耗时间减少。线性支持向量机在各个节点数量条件下,都消耗最多时间,特别是在数据集2的条件下,实际上数据已经线性不可分。在各种节点数情况下,K近邻一直消耗最少时间,决策树次之,支持向量机花费的时间最久,采用RBF的SVM需要运算核函数,花费时间更多,而线性支持向量机由于数据线性不可分,耗费时间最久。
表2 1000个节点时不同算法的运行时间 /ms

KNNLinearSVMRBFSVMDecisionTree数据集154022863429802数据集253146775375801

图8 数据集1不同点数所花费时间比

图9 数据集2不同点数所花费时间比
下面分析不同节点数在各种算法下分类精度,图10展示了在数据集1时的分类精度,从图中可以看出,分类精度差别不是很大,其中以线性支持向量机精度最低。

图10 数据集1不同点数分类精度比较
图11展示了在数据集2时分类精度,对于此类数据集,线性支持向量机分类效果明显很差,大部分情况下分类精度小于0.5。从图10和图11可以知道,节点数量对分类算法的影响比较小,数据集的结构对算法的分类精度有较大影响。

图11 数据集2不同点数分类精度比较
4 结束语
本文分析4种基本分类算法参数作用,通过设置其主要参数,比较算法参数和节点数量对算法精度影响。通过设置最佳参数和使用生成数据集,分析不同噪音参数时分类算法的分类精度及运行所需时间,讨论算法分类结果的基本特点。通过仿真实验表明:对于二维数据的处理,KNN在这4种分类算法上拥有最好分类能力并且消耗了最少的运行时间。根据工作原理推断在高维数据大量数据情况下,KNN和RBF SVM应该具有很好的分类能力,为处理高维数据提供了可靠的依据。
[1] 塞巴斯蒂安·拉施卡. Python机器学习[M]. 北京:机械工业出版社, 2017:55-56.
[2] 宋晖,薛云,张良均. 基于SVM分类问题的核函数选择仿真研究[J]. 计算机与现代化, 2011(8):133-136.
[3] 肖永良,朱韶平,刘文彬,等. 基于优化支持向量机的高校教师绩效评价研究[J]. 赤峰学院学报(自然科学版), 2014(24):25-27.
[4] 尚丹. 基于参数优化的SVM分类器在肺癌早期诊断中的应用[D]. 郑州:郑州大学, 2014.
[5] 崔君荣,苑薇薇. 利用智能算法优化支持向量机参数[J]. 河北科技师范学院学报, 2017,31(1):34-38.
[6] 徐晓明. SVM参数寻优及其在分类中的应用[D]. 大连:大连海事大学, 2014.
[7] Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction[M]. 2nd ed. Springer New York, 2009:463-468.
[8] 曾勇. 广义近邻模式分类研究[D]. 上海:上海交通大学, 2009.
[9] Boyd S, Vandenberghe L. 凸优化[M]. 王书宁,许鋆,黄晓霖译. 北京:清华大学出版社, 2013:42-46.
[10] 周志华. 机器学习[M]. 北京:清华大学出版社, 2016:123-124.
[11] 奉国和. SVM分类核函数及参数选择比较[J]. 计算机工程与应用, 2011,47(3):123-124.
[12] 梁礼明,钟震,陈召阳. 支持向量机核函数选择研究与仿真[J]. 计算机工程与科学, 2015,37(6):1135-1141.
[13] 陈辉林,夏道勋. 基于CART决策树数据挖掘算法的应用研究[J]. 煤炭技术, 2011,30(10):164-166.
[14] 齐乐,岳彩荣. 基于CART决策树方法的遥感影像分类[J]. 林业调查规划, 2011,36(2):62-66.
[15] 张亮,宁芊. CART决策树的两种改进及应用[J]. 计算机工程与设计, 2015(5):1209-1213.
[16] 冯新刚. 支持向量机核函数选择方法探讨[D]. 赣州:江西理工大学, 2012.
[17] 魏峻. 一种有效的支持向量机参数优化算法[J]. 计算机技术与发展, 2015,25(12):97-100.

