基于杠杆法的两行星排行星齿轮变速器传动方案分析

白传鑫 刘 凯 马朝锋

（西安理工大学 机械与精密仪器工程学院，西安 710048）

液力自动变速器由液力变矩器、行星齿轮变速器和电子液压控制系统三部分组成，本文主要研究对象为行星齿轮变速器。行星齿轮变速器主要结构包括行星排和控制元件（离合器、单向离合器和制动器）。行星齿轮变速器的作用是改变传动比或传动方向。行星排多采用内啮合形式，由于各齿轮的模数小，并且采用共轴式传动，相较于平行轴式齿轮变速箱，在传递功率相同的条件下，其能够在很大程度上缩小尺寸并减轻重量，同时可以实现同向、同轴减速传动。

由于单排行星齿轮机构变速范围有限，不能满足汽车的实际需求，所以液力自动变速箱通常由多个单排行星排和多组换挡执行元件组成。通过控制接合或分离不同的控制元件，人们可以获得不同挡位的速比。因此，其结构相对复杂，组合形式繁多。

本文主要对两行星排组成的行星齿轮变速器的组成结构进行分析，介绍两行星齿轮变速器中典型的机构类型。同时，结合几何方法，即杠杆法，分析两行星排齿轮变速的结构特点，计算各典型机构的传动比，为变速器设计提供参考。

1 杠杆法相关理论

杠杆法是用垂直布置的杠杆系等效替代行星齿轮机构，将行星齿轮机构的分析转化为垂直布置杠杆系的分析[1]。

1.1 单行星排等效杠杆法

杠杆法是将一个行星排等效为一根三支点杠杆。对于单级式行星排，如图1（a）所示，中间支点为行星架（PC），两端支点分别为太阳轮（S）和齿圈（R）。对于双级式行星排，如图1（b）所示，中间支点为R，两端支点分别是PC和S。其中，S到PC的距离与R到PC的距离之比为K，即行排特性系数[2]。

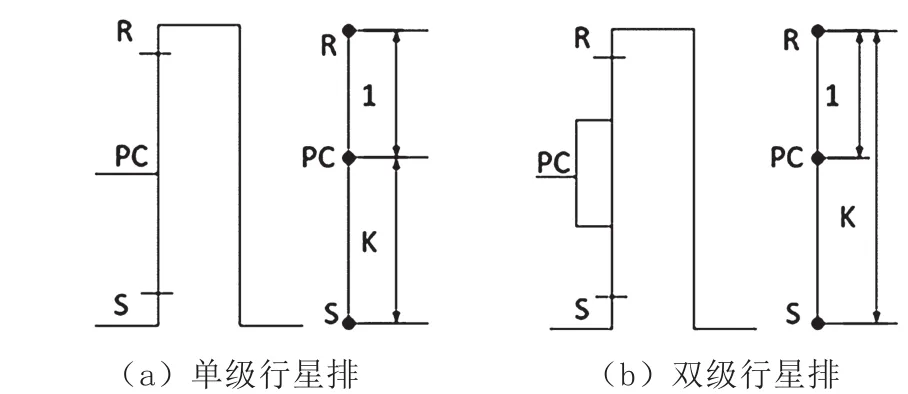
图1 单行星排等效杠杆

代替行星排的垂直杠杆，其转速方程和力矩方程与行星排的相吻合。行星排三元件的转速和力矩分别转化为支点的水平速度和水平力[3]。

1.2 两行星齿轮传动等效杠杆法

杠杆法把不同行星排数组成的两自由度固定结构行星齿轮机构看作行星变速器基本组成单元，它是行星齿轮变速器不能再分割的基本运动构件单元，即基本组成单元就是不同支点数的单杠杆。

行星齿轮变速器可用传动简图来表示，杠杆法中采用与行星排数相对应的3支点杠杆组成的杠杆图来表示，这种与传动简图完全对应（行星排数和构件间连接关系一一对应）的杠杆图被称为分杠杆图。在分杠杆图上，相连的节点可合并成一个点，因此双行星排组成的两自由度固定结构行星机构可合并为一个4支点杠杆[4]。

2排行星排的连接关系有两种，即串联关系和并联关系。串联关系是指两行星排各构件之间只有一组连接关系，并联关系是指两行星排各构件之间存在两组连接关系。多行星排并联时，在分杠杆图中，连接点用一水平线段表示；在合杠杆图中，相互连接的部分合并为1个支点。同时要对杠杆的力臂进行调整，要保证连接部分合并点之间的力臂长度相等，且各杠杆力臂长度比值不变[5]。

1.3 等效杠杆法的缺陷及补充

对于两排行星齿轮变速器，原有杠杆法没有给出串联行星排杠杆图的表示方法，无法分析行星排串联时行星齿轮变速器各挡位的传动情况。因此，需要对原有杠杆法进行补充。

两行星排串联时，在分杠杆图中，连接点用一水平线段表示；在合杠杆图中，相互连接的部分合并为1个支点。同时要保证原杠杆的力臂长度不变。

2 并联两行星排的传动方案综合

首先考虑两单级式行星排。从杠杆图上可知，前、后排杠杆各有三个支点S1，PC1，R1和S2，PC2，R2，根据不同节点相互连接的可能性进行分析，共有12种方案，四类连接方式，如表1所示。

在变速器设计时，应避免太阳轮与圈相连，以防止叠套，故方案（2）、方案（8）、方案（10）和方案（12）不满足要求。同样，两组同名构件相连的方案（1）、方案（6）、方案（7）均不能满足变速器挡位的设计要求（具有1个倒挡，1个直接挡和2～4个减速挡）。故上述方案共有5种情况符合设计要求，分别是方案（3）、方案（4）、方案（5）、方案（9）和方案（11），其分杠杆图如图2所示。

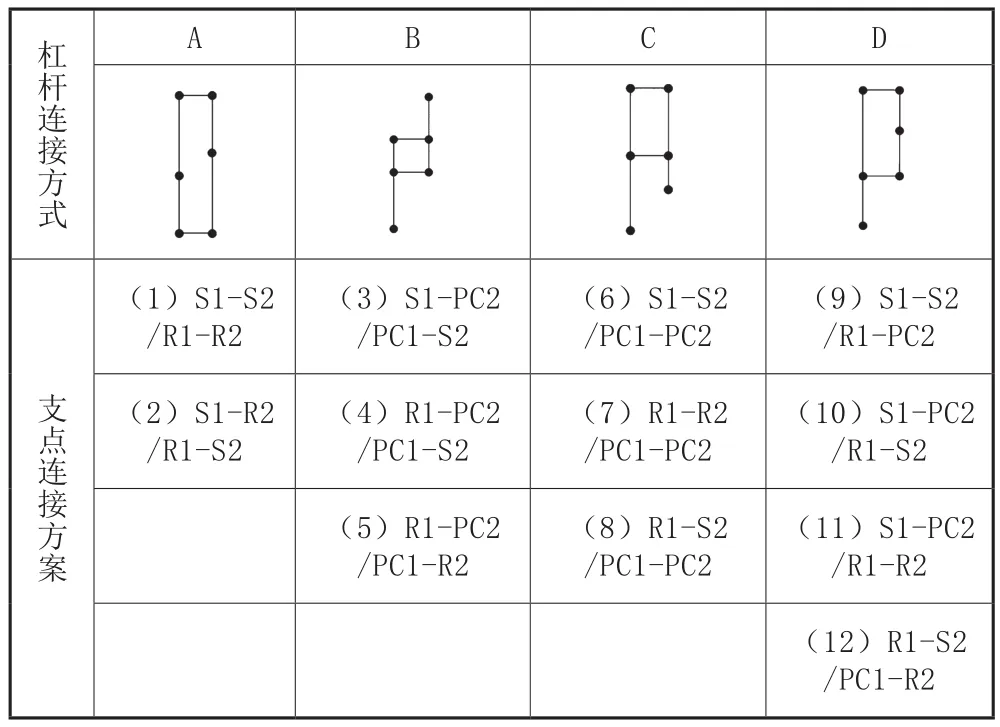
表1 两行星排并联方案

图2 两单级行星排可行方案

其中，方案（9）即为辛普森式方案，方案（5）为CR-CR式方案，也称为辛普森改进型。这两种结构是两排行星齿轮变速器的常用结构，应用广泛，特点为结构较简单且换挡执行元件少。

其次，与两单级式行星排类似，一单级式与一排双级式所组成的行星齿轮变速器同样有12种可能组合。通常情况下，一单级式与一双级式行星齿轮变速器前后行星架共用一个行星轮，即行星架为连接两排行星排的公共构件之一，包括S1-S2/PC1-PC2、R1-R2/PC1-PC2和R1-S2/PC1-PC2三种连接形式。

同样，由于太阳轮与齿圈相连，易出现叠套，故R1-S2/PC1-PC2不符合设计要求。其中，R1-R2/PC1-PC2即为拉维奈尔赫式行星齿轮变速器。与辛普森式和CR-CR式相比，拉维奈尔赫式构件数有所增加，结构较为紧凑，符合变速器设计要求，它们也是两行星排行星齿轮变速器的优选结构。

2.1 辛普森行星齿轮机构分析

辛普森行星齿轮变速器是一种典型结构，其传动简图如图3（a）所示，图3（b）是其等效分杠杆图。其结构特点是：两个行星排共用一个太阳轮，前齿圈和后行星架连接在一起，通过输出轴传递动力，可实现2个减速挡、1个直接挡和1个倒挡，无超速挡。其径向尺寸较小，轴向尺寸较大，该机构常用于后桥驱动的轿车上，是行星齿轮变速器早期常用的结构形式。

该机构的控制元件包括2个离合器C1/2和CR，2个制动器B1/R和B2。设两个行星排特性系数分别为a和b，比例常数为1。如图3（c）所示，通过分杠杆图，人们可以画出合杠杆图。通过比例换算，该四支点杠杆中各段的杠杆比为：a:1:[（a+1）/b]。

由于该行星齿轮变速器的输入转速ni为1个单位转速，制动点转速为0。然后，确定不同挡位下的输入点和制动点，连接输入点和制动点，人们可以得到各挡位的速度线，其与输出轴x交点的横坐标即为输出转速大小。输入转速与输出转速之比即为传动比。图3（d）为各挡的速度线图。

图3 辛普森行星齿轮变速器等效杠杆

下面对各挡传动比进行分析：

1挡时，C1/2和B1/R工作，后排齿圈与输入轴相连，前排行星架固定。输入点为R2，制动点为PC1。如图3（d）所示，1挡转速线与x轴交点的横坐标即为转速线。由相似三角形关系可得，传动比为输入点到制动点的距离与输出点到制动点的距离之比。故1挡传动比为：

2挡时，C1/2和B2工作，后排齿圈与输入轴相连，太阳轮固定。同理，2挡传动比为：

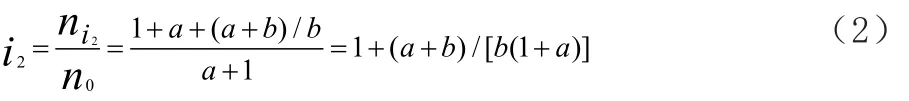
3挡时，C1/2和CR工作，后排齿圈与太阳轮固定连接，并与输入轴相连，此时整个行星齿轮机构作为一个整体运动，传动比为1，为直接挡。

R挡时，CR和B1/R工作，前排太阳轮与输入轴相连，前排行星架固定，则R挡的传动比为：

表2为辛普森行星齿轮变速器传动比计算表。

表2 辛普森行星齿轮变速器各挡传动情况

2.2 CR-CR行星齿轮机构分析

CR-CR式，即改进型辛普森行星齿轮机构，如图4（a）所示，其等效杠杆图如图4（b）、4（c）所示。它的结构特点是：前排齿圈与后排行星架为一体；后排齿圈与前排行星架为一体；两个太阳轮独立。后排行星架为输出元件。其可实现2个减速挡、1个直接挡、1个超速挡和1个倒挡。

它采用3个离合器C，4个制动器B和3个单向离合器F。设前、后行星排特性系数分别为a和b，取比例常数为1，则前排S1到PC1的距离与PC1到R1的距离之比为a:1，后排S2到PC2的距离与PC2到R2的距离之比为b:1，则4支点竖直杠杆图中各段的杠杆比为a:1:b。各挡位的换挡元件及传动比如表3所示。计算与辛普森行星齿轮变速器类似，速度线图如图4（d）所示。

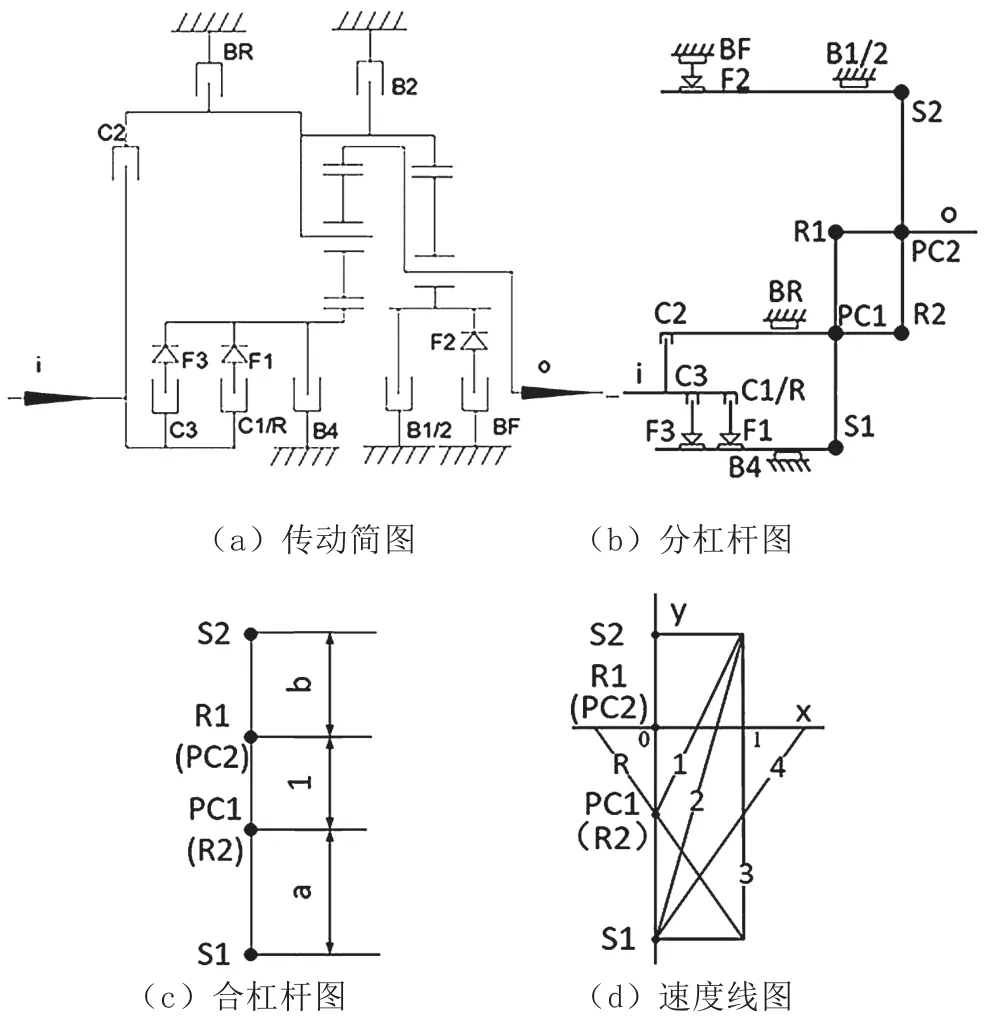
图4 CR-CR行星齿轮变速器等效杠杆

表3 CR-CR行星齿轮变速器各挡传动情况

2.3 拉维奈尔赫行星齿轮机构分析

拉维奈尔赫行星齿轮系统的典型结构如图5（a）所示，其等效杠杆图如图5（b）、5（c）所示。它的结构特点是：两行星排共用1个行星架和1个齿圈，前排为单级式行星排，后排为双级式行星排。齿圈为输出轴，同样可以实现2个减速挡、1个直接挡、1个超速挡和1个倒挡。

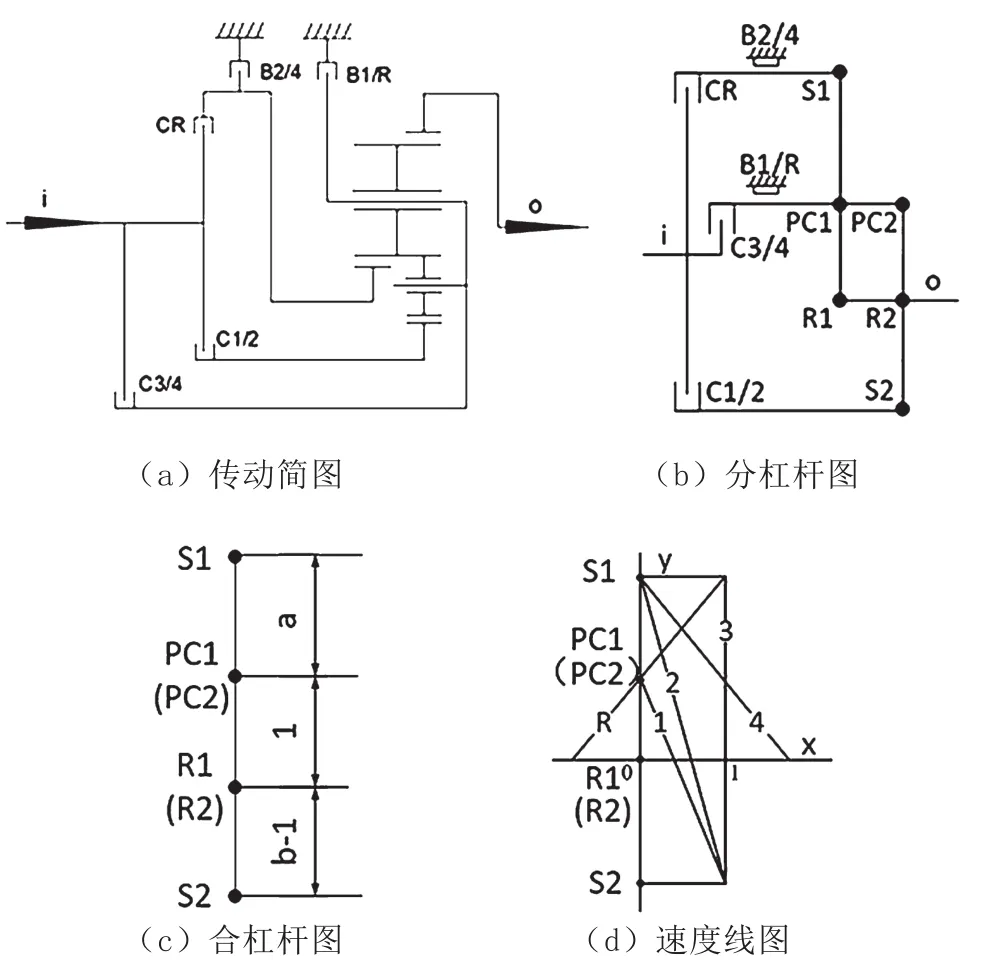
图5 拉维奈尔赫行星齿轮变速器杠杆

拉维奈尔赫行星齿轮机构轴向和径向尺寸均较小，结构紧凑，前、后桥驱动均可采用，其缺点是拆装困难，制造成本较高。它的控制元件包括3个离合器C和2个制动器B。设前、后排齿圈特性系数为a、b，比例常数为1。则前排S1到PC1的距离与PC1到R1的距离之比为a:1，而后排为双行星齿轮机构，S2到R2的距离与R2到PC2的距离之比为（b-1）:1，则该4支点竖直杠杆图中各段的杠杆比为a:1:（b-1）。其各挡位的换挡元件及传动比如表4所示，速度线图如图5（d）所示。

表4 拉维奈尔赫行星齿轮变速器各挡传动情况

3 串联两行星排传动方案综合

原杠杆法对并联行星排提出了等效杠杆法的解决方案，未就串联行星排提出相应的处理方法。串联两排行星排可以等效为5点杠杆。对于串联两行星排，前、后排杠杆共有三类连接方式，共有6种可能组合，详情如表5所示。

表5 两行星排串联方案

这三类方案中，仅有A类方案有一定实用性。其中方案（3）为通用汽车公司研发的5L40E型自动变速器，其传动简图及等效杠杆图如图6（a）、图6（b）和图6（c）所示。它是一种特殊结构的拉维奈尔赫型行星齿轮组，两行星排不仅公用行星架，还公用1组行星架上的齿轮，前排行星架上的内行星轮同时是后排行星架上的外行星轮。这种设计非常巧妙，通过简单的公用关系实现了3个减速挡，1个直接挡、1个超速挡和1个倒挡的组合。

假设前、后行星排特性系数分别为a和b，取比例常数为1，则支点R1、R2分别到公共构件点PC1（PC2）的距离为1，该5支点竖直杠杆图中各段的杠杆比为（a-1）:1:（b-1）。各挡的控制元件、传动比计算公式如表6所示，其传动比计算与辛普森行星齿轮系统类似，速度线图如图6（d）所示。

图6 5L40E行星齿轮变速器杠杆

通过1挡和R挡真实传动比计算，可得a=3.03，b=3.42，带入3、4、5挡传动比计算公式，其数值与实际传动比吻合。这证明了杠杆法在分析通用5L40E型自动变速器各挡动力传递时的正确性。

表6 5L40E行星齿轮变速器各挡传动情况

4 结论

本文将两行星排分为串联和并联两种连接方式，采用杠杆法，分析了两行星排所有可能的传动方案。研究表明，两行星排并联传动方案，可简化为4点杠杆，通常能实现3速和4速。同时，笔者推导出常见并联机构辛普森、CR-CR和拉维奈尔赫各档传动比的计算公式。杠杆法能直观反映出输出速度和传动比的大小，清晰地显示各挡位的输入、输出及制动构件。杠杆法还可以用于分析机构中各构件的转矩和行星齿轮变速器的换挡过程，为控制元件的布置和变速器的设计提供依据。基于现有杠杆法，人们拓展了其适用范围，将两行星排串联传动方案等效为5点杠杆，并通过实例验证了其正确性。

[1]黄宗益，李兴华.轿车自动变速器杠杆分析法[J].传动技术，2002，（3）：18-25.

[2]黄宗益.现代轿车自动变速器原理和设计[M].上海：同济大学出版社，2006：52-56.

[3]黄宗益，贾王欢，李兴华.行星变速器杠杆设计法[J].传动技术，2016，（2）：3-16.

[4]冯樱.运用杠杆法计算汽车行星齿轮变速器的传动比[J].湖北汽车工业学院学报，2008，22（3）：17-20.

[5]何国旗，李兴华.行星齿轮传动分析的新方法[J].机械工程师，2003，5（11）：48-51.