Nonlinear Prediction with Deep Recurrent Neural Networks for Non-Blind Audio Bandwidth Extension

Lin Jiang, Ruimin Hu*, Xiaochen Wang Weiping Tu Maosheng Zhang National Engineering Research Center for Multimedia Software, School of Computer Science, Wuhan University, Wuhan 007, China Institute of Big Data and Internet Innovation, Hunan University of Commerce, Changsha 00, China Software College, East China University of Technology, Nanchang 00, China Collaborative Innovation Center for Economics crime investigation and prevention technology, Jiangxi Province, Nanchang 00,China Hubei Key Laboratory of Multimedia and Network Communication Engineering, Wuhan University, Wuhan 007, China Collaborative Innovation Center of Geospatial Technology, Wuhan 0079, China

I. INTRODUCTION

In modern telecommunications, audio coding becomes an essential technology which attracts lots of attentions. In particular, for mobile applications, packing the data into small space with efcient methods is benecial. The coding algorithms must be fairly simple because mobile processors are relatively not very powerful and less processing leads to lesser use of battery. Audio bandwidth extension(BWE) is a standard technique within contemporary audio codecs to efciently code audio signals at low bitrates [1].

In the audio codecs, the signals are split into low frequency (LF) and high frequency(HF) parts, and are encoded by core codec and BWE respectively. The approach is based on the properties of the human hearing. The hearing threshold for high frequencies is higher than for lower frequencies (except very low frequencies), so high frequency tones are not heard as loud as the same amplitude tones at lower frequencies [2]. Also the frequency resolution of hearing is better on lower frequencies. Therefore, the coding bitrates for HF is far lower than for LF.

Another useful feature of many types of audio samples is that the level of the higher frequencies is usually lower than the level of lower frequencies. And finally, the sound of many musical instruments is harmonic, which means that some properties of the frequency spectrum are very similar in lower and higher frequencies [3]. The similarity of frequency spectrum is also called the correlation between LF and HF.

According to above mentioned properties and feature, on the decode side, the HF signals are usually generated by a duplication of the corresponding decoded LF signals and a priori knowledge of HF. Depending on whether transmitting parameters, the BWE methods have two categories: blind BWE and nonblind BWE. In non-blind BWE, a few parameters of HF are transmitted to the decoder side for reconstructing the high frequency signals.In this paper, we only discuss about non-blind BWE. For the sake of concise narrative, the term non-blind BWE will be replace with abbreviation BWE in the following section.

In the audio coding standard, BWE is a necessary module for coding high frequency signal. For example, MPEG Advance Audio Coding (AAC) used a spectral band replication method (SBR)[4], AMR WB+ used a LPC-based BWE[5], ITU-T G.729.1 used a hierarchical BWE[6], China AVS-M used a LPC-based BWE in FFT domain[7,8], MPEG Union Speech and Audio Coding (USAC)used an enhanced SBR (eSBR)[9], 3GPP EVS used a multi-mode BWE method, including TBE[10], FD-BWE[41] and IGF[42]. There are two main categories of BWE methods:time domain BWE and frequency domain BWE.

The time domain BWE performs adaptive signal processing according to the well-known time-varying source-filter model of speech production [1]. This approach is based on the Linear Predictive Coding (LPC) paradigm(abbr. LPC-based BWE) in which the speech signal is generated by sending an excitation signal through an all-pole synthesislter. The excitation signal is directly derived from a duplication of the decoded LF signals. The all-pole synthesis filter models the spectral envelope and shapes the fine pitch structure of the excitation signal when generating the HF signal. A small number of parameters of HF, as parametric representations of spectral envelope, are transmitted to the decoder side,such as Liner Prediction Cepstral Coefcients(LPCCs), Cepstral Coefficients (CEPs), Mel Frequency Cepstral Coefficients (MFCCs)[11,12], and Line Spectral Frequencies (LSFs)[13]. In order to improve the perception quality of coding, a codebook mapping technique is also introduced for achieving more accuracy presentations of HF envelope [14,15].

As the basic principle of the LPC-based BWE is speech generation model, this approach is widely used in speech coding[5-7,16]. However, because the lower frequencies of voiced speech signals generally exhibit a stronger harmonic structure than the higher frequencies, the duplication of LF excitation should cause too harmonic components on the generated HF excitation signal, which should bring out the objectionable, ‘buzzy’—sounding artifacts [16].

The frequency domain BWE recreates the HF spectral band signals in frequency domain. The basic principle of BWE approach is derived from the human auditory system in which hearing is mainly based on a shortterm spectral analysis of the audio signal.Spectral band replication (SBR) [4] is the most widely used frequency domain BWE method. SBR uses a Pseudo-Quadrature Mirror Filter (PQMF) description of the signal and improves the compression efficiency of perceptual audio codecs. This is achieved by simply copying the LF bands to the HF bands within the used filter bank, followed by post processing (including inverse filtering, adaptive noise addition, sinusoidal regeneration,shaping of the spectral envelope). However, if the correlation between low and high frequency becomes weak, the method will produce artifacts because the harmonic structure of the HF signal is not preserved. To remedy this,some methods were developed to maintain the harmonic structure: the phase vocoder driven Harmonic Bandwidth Extension (HBE)[17], the Continuously Modulated Bandwidth Extension (CM-BWE) using single sideband modulation [18], QMF-based harmonic spectral band replication [19], MDCT-based harmonic spectral bandwidth extension method[20]. These methods significantly improved the perception quality of coding. However,the coding artifacts are still existed inevitably because the replication method from LF to HF needs require the strong correlation between LF and HF [21].

The above mentioned BWE methods have two steps to generate the HF signal. First, rebuild the coarse HF signal by copying LF to HF at the corresponding present time frame.Second, generate the final HF signal by envelope adjustment using the transmitted HF envelope data. On therst step, the similarity between the coarse HF and original HF will directly affect the perception quality of coding.Consequently, the weak correlation between HF and LF will result in the degraded perception quality of coding. Our investigation found that the correlation existed in the LF signal of context dependent frames in addition to the current frame. In this paper, our main goal is to achieve more accurate coarse HF signal for improving the perception quality of coding.We propose a novel method to predict the coarse HF signal by deep recurrent neural network using the context dependent LF signal.Then we replace the conventional replication method by our method in the reference codecs.Moreover, in order to conrm the motivation of our method, we also propose a method to quantitatively analyse the correlation between LF and HF signal.

The paper is organized as follows. Section 2 describes the motivation of this paper. In section 3, the prediction method of coarse HF signal is given, while the performance of proposed method and comparison with others are shown in section 4,nally section 5 presents conclusion of this paper.

Fig. 1. Generic scheme of BWE.

II. MOTIVATION

2.1 Overview of BWE scheme

The generic scheme of BWE is shown ingure 1. In generic scheme of BWE, according to the perceptive difference of human system for HF and LF, the full band input signalSfullis split into HF signalShfand LF signalSlf.The LF signal is coded using a core codec,such as algebraic code excited linear prediction (ACELP)[5,7,8,10], or Transform Coded Excitation (TCX) algorithm[5,7,8], or MDCT-based Coding[6,9,10,36]. While HF signal is usually without an explicit waveform coding,only a small number of HF parametersPhfare extracted and transmitted to the decoder side.On the decoder side, the final HF signalS’hfis recreated using coarse HF signalChfand decoded HF parametersP’hf. The coarse HF signal is usually generated by the decoded LF signalS’lf. To produce a pleasant sounding HF signal, an intuitive approach is to increase the HF parameters. However, it is in conict with requirement of low bitrate. Some approaches are developed to enhance the similarity between coarse HF and original HF.

In time domain BWE, the coarse HF signal is usually derived from the decoded LF excitation signal. To preserve the harmonic structure of the HF excitation signal, a nonlinear function is used [16,22,]. In [23], the HF excitation signal is generated by upsampling a low band fixed codebook vector and a low band adaptive codebook vector to a predetermined sampling frequency. In frequency domain BWE, the coarse HF signal is usually derived from a duplication of decoded LF subband signal in frequency domain. To preserve the harmonic structure of original HF, some post processing is usually introduced, such as inverseltering, adaptive noise addition, sinusoidal regeneration, shaping of the spectral envelope [20], single sideband modulation [18],and a phase vocoder [17].

The above approaches are conducive to improve the similarity of coarse HF with original HF. However, the improvement is limited when the correlation between HF and LF signal becomes weak. More importantly, we found only the current frame decoded LF signal is used to generate coarse HF in existing method. According to the physical properties of the audio signal, we consider the correlation also exists in the LF signal of context dependent frames.

2.2 Correlation analysis between HF and LF

The motivation for all bandwidth expansion methods is the fact that the spectral envelope of the lower and higher frequency bands of the audio signal is dependent, i.e., the low band part of the audio spectrum provides information about the spectral shape of the high band part. The level of dependency will affect the accuracy of reconstructed HF signal. In existing BWE methods, only the current frame LF signal is used to recreate the coarse HF. The utilization of current frame is due to the shortterm correlation of audio signal. However,there is also a long-term correlation when fundamental frequency of voice changes slowly[24]. To reveal the long-term correlation for recreating the HF signal, we quantitatively analyse the correlation using mutual information between HF and LF.

Taking into account the uncertainty and nonlinearity of audio signal, mutual information is an appropriate measure of correlation[25,26]. The mutual information (MI) between two continuous variablesXandYis given by[27]:

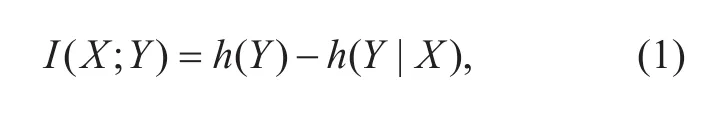
whereh(Y) is the differential entropy ofYand is defined by an integration over the value spaceΩYofY:

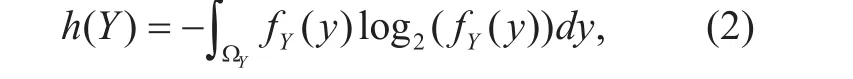
wherefY(y) denotes the probability density function (pdf) ofY. The conditional differential entropyh(Y|X) ofYgivenXis dened as:

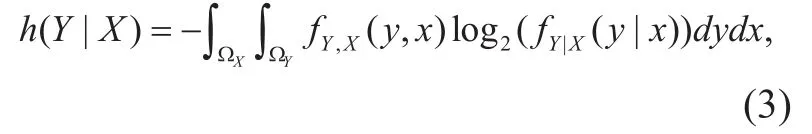
whereΩXis the value space ofXandfY,X(y,x)is the jointpdfofXandY. Throughout our correlation analysis,Xis a frequency spectral amplitude vectorALrepresenting LF band andYis a frequency spectral amplitude vectorAHrepresenting the HF band. The mutual information is dened in the discrete forms:

wherep(aL,aH) is the joint probability of LF and HF,p(aL) andp(aH) denotes the prior probability of LF and HF respectively.

In order to quantitatively analyse the correlation of various types of sound, we calculate theMIvalueunder different frame-shift, wheredenotes thei-th frame HF, thedenotes the (i-t) frame LF,tis frame shift. In figure 2, whent=0, the correlation is the greatest than others (the greater the MI value, the higher the correlation). It is easy to understand, because the HF and LF come from the same one frame. Just as we proposed the hypothesis in section 2.1, there also exists the correlation between thei-th frame HF and thei-1,i-2,i-3, … frame LF signal. Moreover, we also give the average MI values of various types of sound (e.g. speech,music and instrument) for evalu ating the correlation (seegure 3). Ingure 3, we alsond that the HF signal is not only associated with the LF signal of the current frame, but also associated with the LF signal of the front frame.All of this shows that HF construction can be derived from the LF signal of context dependent frames besides the current frame.

Fig. 2. The MI (bits) of bagpipes sound under different frame- shift.

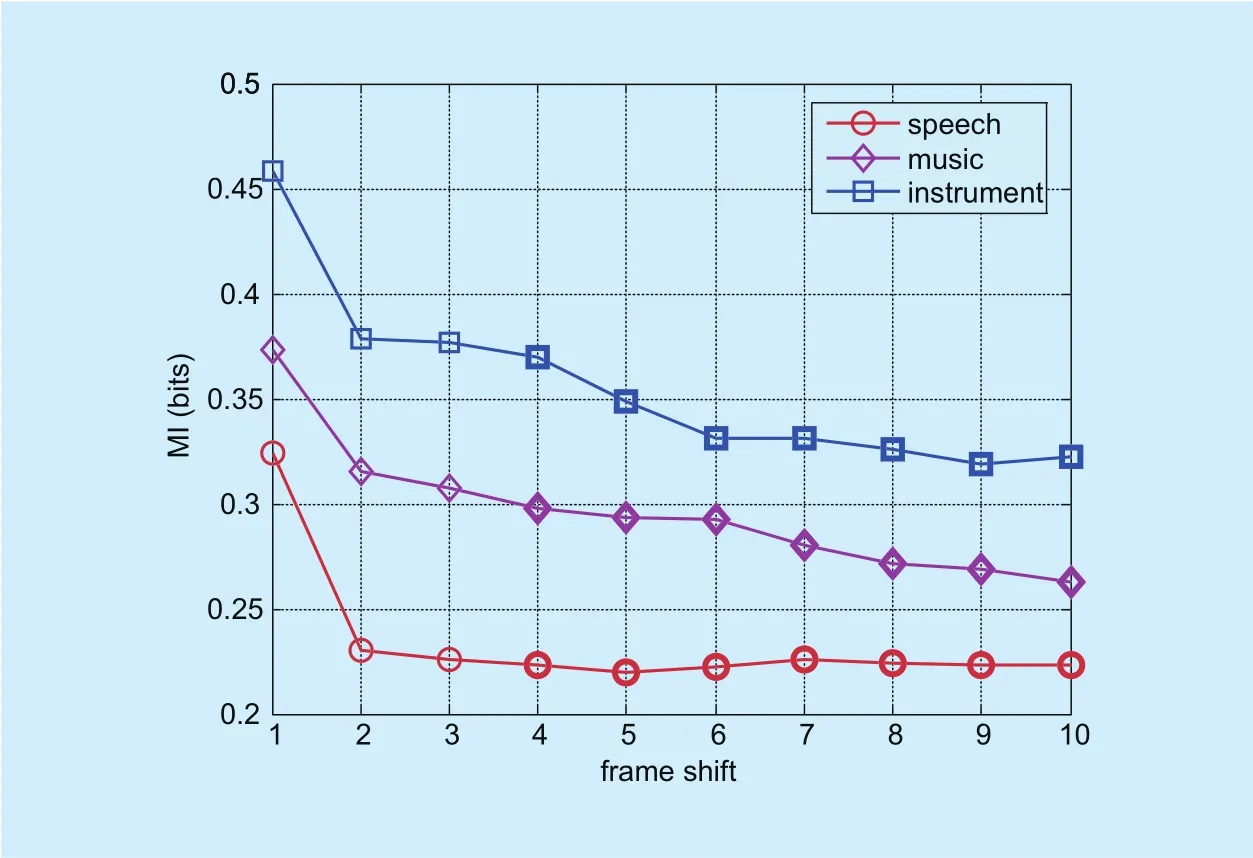
Fig. 3. The average MI (bits) of various types of sound under different frame-shift.

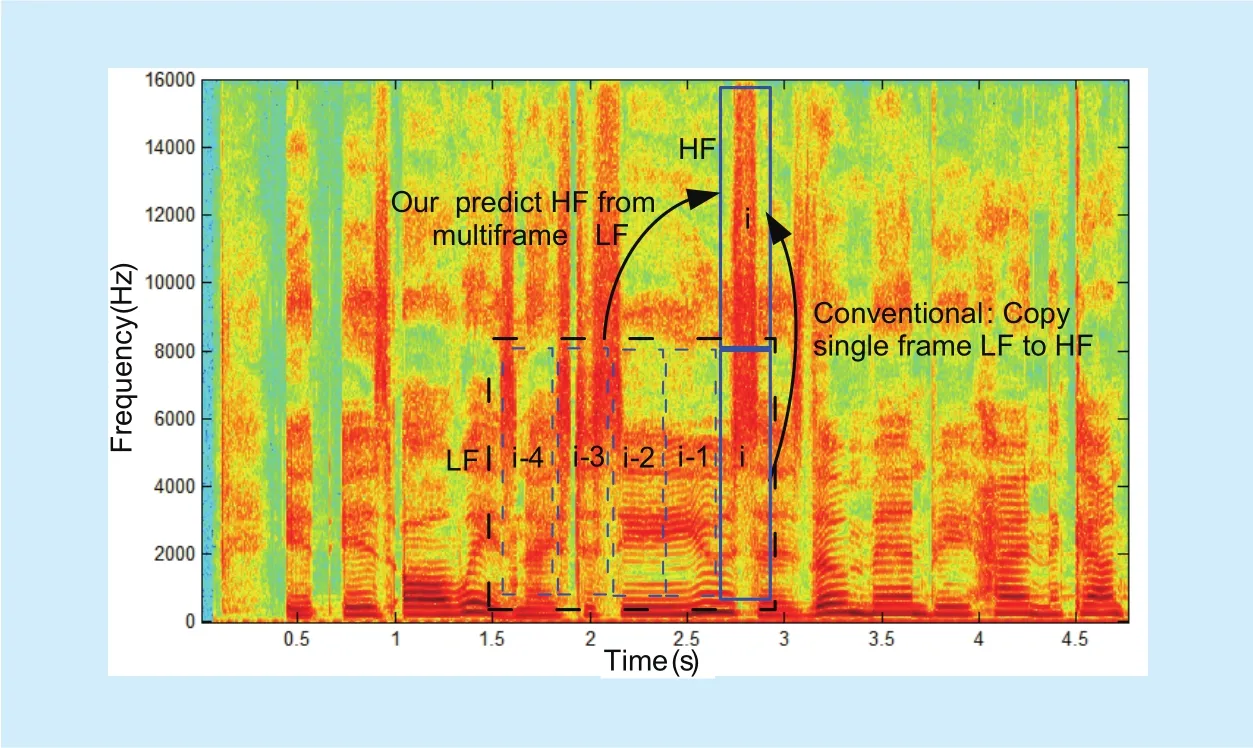
Fig. 4. The conceptual comparison between conventional and our method for generating coarse HF signal on Spectrogram.

2.3 Selection of prediction method

The purpose of this paper is to predict the coarse HF signal from LF. In particular, we will establish a nonlinear mapping model from LF to HF for achieving more accurate coarse HF signal. In blind bandwidth extension, nonlinear mapping model as a generic method is developed for expanding the wideband speech signal. In these methods, neural network is a usual selection due to its strong capacity on modelling [28-30]. As the mapping from LF to HF is extreme complicated, the model ability of previous shallow network is inadequate. In our previous work, we used a deep auto-encoder neural network to predict the coarse signal of HF [31]. The method significantly improved the perception quality of coding.Since only using the current frame LF signal,the improvement is limited when the correlation between LF and HF becomes weak.

According to the correlation analysis of above mentioned, the correlation existed in the LF signal of context dependent frame besides the current frame. The selected mapping method is required having a model capacity on time series signal. The recent deep recurrent neural networks showed an excellent performance for large scale acoustic modelling [32].Consequently, we select it as a model tool for predicting the coarse HF signal.

III. THE PREDICTION METHOD OF COARSE HF SIGNAL

3.1 Problem statement

In previous work, the coarse HF signal is usually generated by a duplication of the corresponding current frame LF signal. According to the correlation analysis in section 2, we will establish a nonlinear mapping model to predict the coarse HF signal using the context dependent LF signal. The conceptual comparison between conventional and our method is shown ingure 4. The prediction task can be formulated as a generative model problem in mathematical. This reformulation allows applying wide range of well-established methods.

be the training set whereliandhiis thei-th frame decoded LF signal and the original coarse HF signal, respectively. Let’s divide the dataset into train and validation setswith sizeNlandNvcorrespondingly. Further we introduce the set of prediction functionin which we want tond the best model. Assuming neural network with thexed architecture, it is possible to associate the set of functionFwith the network weights spaceWand thus functionfand vector of weightsware interchangeable.

Next step is to introduce the loss function.As in almost all generative models, here we are interested in accuracy error measure. In particular, we wishnd a “perfect” prediction function to generate the coarse HF signal with minimal error. We definedLoss(h,y) as the loss function, wherehis the original coarse HF signal,y=f(l) is the prediction value of the model from decoded LF signall. Assuming that there is a “perfect” predictionfF*in prediction function setF, our task is tondfF*in the best possible way. According to statistical learning theory[43], the risk associated with predictionf(l) is then dened as the expectation of the loss function :

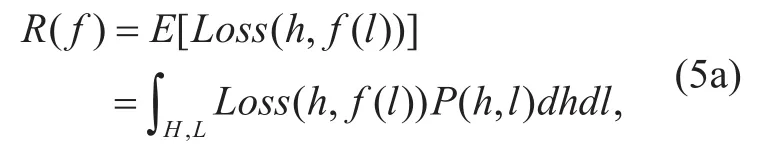
whereP(h,l) is a joint probability distribution over coarse HF signal train setHand decoded LF train setL. Our ultimate goal is to find a prediction functionfF*among axed class of function setFfor which theR(f) is minimal:

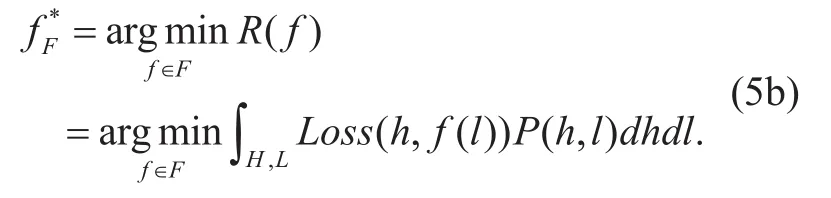
In general, the riskR(f) cannot be computed directly because the distributionP(h,l) is unknown to the learning algorithm. However, we can compute an approximation offF*, calledempirical risk[43], by averaging the loss function on the training set:

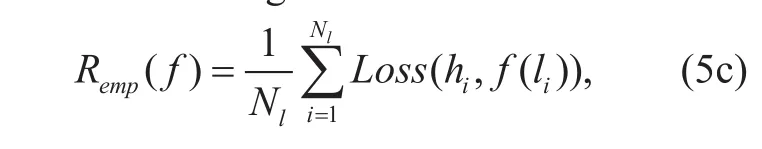
whereNlis the size of training set.Empirical risk minimization[43] principle states that the learning algorithm should choose a predictionfˆ which minimizes the empirical risk:

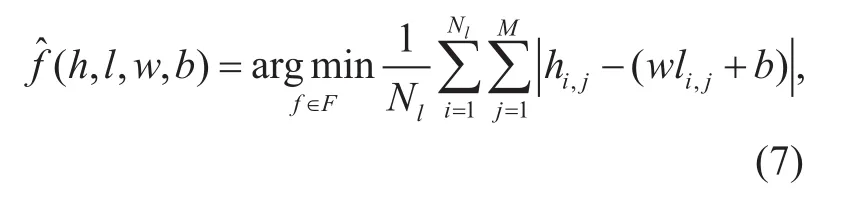
whereidenotes frame index,jis the frequency spectrum coefcient index, andMis frame length,wandbis the network weights and bias item, respectively. Common approach here to reduce overtting is to check the validation error from time to time during the optimization process and to stop when it starts growing. Due to the validation error will go up and down in a short time, the criterion of starts growing is implemented on the consecutive frames, e.g. 5 frames. If the validation error goes up steadily, we will stop it.

3.2 Prediction method

The purpose of recurrent neural networks(RNNs) was put forward to deal with time-serial data. Motivated by its superior performance in many tasks, we propose a nonlinear mapping model to predict the coarse HF signal using deep long short-term memory recurrent neural networks.

3.2.1 RNN

Recurrent neural networks allow cyclical connections in a feed-forward neural network[33]. Different from the feed-forward ones,RNNs are able to incorporate contextual infor-mation from previous input vectors, which allows them to remember past inputs and persist in the network’s internal state. This property makes them an attractive choice for sequence to sequence learning. For a given input vector sequence x=(x1,x2,…,xT), the forward pass of RNNs is as follows:

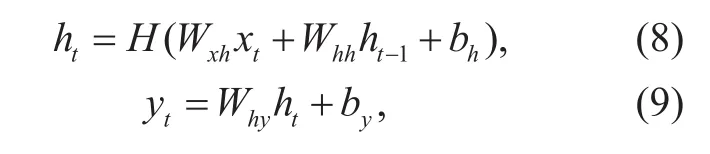
wheret=1,…,T, andTis the length of the sequence; h=(h1,h2,…,hT) is the hidden state vector sequence computed from x; y = (y1,y2,…,yT) is the output vector sequence; W are the weight matrices, where Wxh, Whhand Whyare the input-hidden, hidden-hidden and hidden-output weight matrices, respectively.bhandbyare the hidden and output bias vectors, respectively, andHdenotes the nonlinear activation function for hidden nodes.

For our prediction system, because of the context dependency correlation phenomenon,we desire the model to have access to both past and future context. But conventional RNNs can only access the past context and they ignore the future context. So the bidirectional recurrent neural networks (BRNNs) are used to relieve this problem. BRNNs compute both forward state sequenceh→and backward state sequenceh←, as formulated below:

Fig. 5. Long short-term memory (LSTM) [34].

3.2.2 LSTM-RNN

Conventional RNNs can access only a limited range of context because of the vanishing gradient problem. Long short-term memory(LSTM) uses purpose-built memory cells, as shown in figure 5 [34], to store information which is designed to overcome this limitation[34]. In sequence-to-sequence mapping tasks,LSTM has been shown capable of bridging very long time lags between input and output sequences by enforcing constant error flow.For LSTM, the recurrent hidden layer functionHis implemented as follows:

whereσis the sigmoid function;i,f,o,aandcare input gate, forget gate, output gate, cell input activation and cell memory, respectively.τandθare the cell input and output nonlinear activation functions, in whichtanhis generally chosen. The multiplicative gates allow LSTM memory cells to store and access information over long periods of time, thereby avoiding the vanishing gradient problem.

3.2.3 DBLSTM-RNNs-based Prediction Method

In order to accurately predict the coarse HF signal using the context dependent decoded LF signal, we design the DBLSTM-RNNs with the dilated LSTM, as shown in figure 6[35]. The dilated LSMT can make sure the predicted coarse HF signalH(ht|lt,lt-1,lt-2,…,l1)emitted by the model at timesteptdepend on any of the previous decoded LF signal at timestepst,t-1,t-2, ... ,1. A dilated LSTM is a LSTM which is applied over an area larger than its length by skipping input values with a certain step.

Stacked dilated LSTM efficiently enable very large receptive fields with just a few layers, while preserving the input resolution throughout the network. In this paper, the dilation is doubled for every layer up to a certain point and then repeated: e.g.

1,2,4,…,512, 1,2,4,…,512, 1,2,4,…,512.

The intuition behind this configuration is two-fold. First, exponentially increasing the dilation factor results in exponential receptiveeld growth with depth. For example each 1,2, 4,…, 512 block has receptive field of size 1024. Second, stacking these blocks further increases the model capacity and the receptiveeld size.

Learning DBLSTM-RNNs can be regarded as optimizing a differentiable error function:

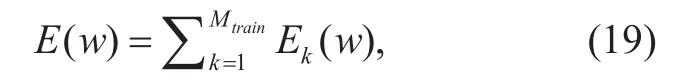
whereMtrainrepresents the number of sequences in the training data and w denotes the network inter-node weights. In our prediction system, the training criterion is to minimize the sum of squared errors (SSE) between the predicted value and the original coarse HF signal. We use back-propagation through time(BPTT) algorithm to train the network. In the BLSTM hidden layer, BPTT is applied to both forward and backward hidden nodes and back-propagates layer by layer. After training network, the weight vectors w and bias vectors b will be determined, we can use the network to predict the coarse HF signal with the decoded LF signal, as formulated below:

wherek=i-m+1,mis the timestep, andm=2d,ddenotes the depth of DBLSTM-RNNs.

六是财政支持低保政策实施的手段单一。财政部门对低保对象的支持局限于低保补贴，对低保对象从事创业与就业的支持政策不明确，如低保户创业和就业的启动资金支持或贷款贴息支持政策不明确，缺乏激励。

IV. THE EXPERIMENT AND EVALUATION

In order to verify the validity of the proposed method, we used the DBLSTM-RNNs instead of the conventional replication method to generate the coarse HF signal on the reference codecs. For testing the ubiquitous capacity of our method, we selected 6 representative reference codecs as evaluation object.

In this section, we first describe the reference codecs for evaluating the performance of proposed method. Then we train the DBLSTM-RNNs architecture on different reference codecs. Finally, we show the experimental results of subjective listening test,objective test and comparison of computation complexity.

4.1 Test reference codecs

(2)WB+ 3GPP AMR WB+ is an extended AMR-WB codec that provides unique performance at very low bit rates from below 10.4 kbps up to 24 kbps [5]. Its HF signal is encoded by a typical time domain BWE method(LPC-based BWE), and the coarse HF signal is achieved by copying the decoded LF excitation signals. The bitrate is set to 16.4 kbps in our experiments.

(3)AVS Audio and Video coding Standard for Mobile (AVS-M, submitted as AVS Part 10) is a low bitrate audio coding standard proposed for the next generation mobile communication system [7,8]. It is also therst mobile audio coding standard in China. Its BWE is similar to WB+, and the coarse HF signal derived from a duplication of decoded LF excitation signal. Like as WB+, the bitrate is set to

16.4 kbps for testing.

(5)EVS The codec for Enhanced Voice Services, standardized by 3GPP in September 2014, provides a wide range of new functionalities and improvements enabling unprecedented versatility and efficiency in mobile communication [10]. For upper band coding,EVS uses different BWE methods based on the selected core codecs. On LP-based coding mode, TBE and multi-mode FD-BWE method is employed. On MDCT based TCX coding mode, an Intelligent Gap Filling (IGF) tool is employed, which is an enhanced noiselling technique toll gaps (regions of zero values)in spectra.

(6)DAE This is an improved version of AVS P10 from our previous work [31]. The coarse HF signal is predict from the LF signal of current frame by a deep autoencoder. This method is selected as reference codecs because of its representative of prediction.

The more details of test reference codecs are listed on Table 1.

Table I. The details of test reference codecs.

4.2 Experiment setup

All networks are trained on an about 50 hour dataset consisting of TIMIT speech, Chinese speech, natural sounds and music. We randomly divided the database into 2 disjoint parts:80% for training, 20% for validation. Due to the different input signal on six test reference codecs, the training process is carried out separately on six reference codecs. The inputs of networks are the decoded LF signals which are extracted from each reference codecs, respectively. To the supervised data, the original coarse HF signals are extracted on the encoder side at each reference codecs, respectively.The frequency ranges are listed in Table 1.

Our goal is to predict the coarse spectrum,so the parameters remain untouched. For AAC+ and USAC, SBR and eSBR technique,the QMF coefficients of decoded LFs as input signal, due to the complex form of QMF,the real and imaginary coefficients are input separately, and the HF coarse spectrum also is predicted separately. For WB+ and AVS,the excitation of decoded LFs as input signal,and the excitation signal of HFs is predict. For DAE, the MDCT coefcients of decoded LFs as input, and the HF MDCT coefficients are predicted. For EVS, our method is implemented just on TBE, and the proposed model replaced the nonlinear function module on TBE.The excitation of decoded LFs and HFs as input and output of model respectively. For all reference codecs, the smoothing process was implemented on time domain for the generated final HFs. We used an energy suppressed method between frames to reduce the noise.

According to the Correlation analysis in section 2.2, the correlation is exists in the previous consecutive frames. In our implementation, we generally use the previous 5 frames decoded LFs signal to predict the current frame HFs coarse spectrum. However, the weak correlation (e.g. transient and other non-stable frames) maybe result in the strong distortion. In order to remedy it, before predicting, we implement the transient detec-tion on decoded LFs, if the frame is transient signal, we will don’t use it to predict. If the transient frame exceeds 2, we will only use the current frame to predict.

The training of networks architectures is implemented on a CPU-GPU Cluster which is a high performance computing system of Wuhan University [37]. We use the asynchronous stochastic gradient descent (ASGD)optimization technique. The update of the parameters with the gradients is done asynchronously from multiple threads on a multicore machine. The number of hidden layers is set based on the observation of Spectral Distortion (SD) between outputs of model and original coarse HF signal (see figure 7). The results show that the SD value is dropt with the increase of the networks depth, and the change levelled off at depth 10. Taking into account the computational complexity, we set the networks depth to 10, and the predicted timestep is 210=1024.

Fig. 7. The Spectral Distortion (SD) values of under different depth of networks.

4.3 Subjective evaluation

For evaluating the perception quality of coding, a subjective listening test was conducted using the comparison category rating (CCR)test [38]. 12 expert listeners participated in a CCR test compare pairs of audio samples, and evaluate the referenced one in each comparison with the replaced one (using proposed method to predict the coarse HF signal) using a discrete 7-point scale that ranges from much worse (−3) to much better (3). The resulting average score is known as the comparison mean opinion score (CMOS). For CMOS value, the score increased by 0.1 indicates significant improvement. By the way, the threshold is not a standard criterion. We use it is because it is a habitual rules on China AVS Workgroup,they usually accept a new technical proposal use this criterion [44,45]. The MPEG audio test files are used as test material (see table 2.), which is a well-known testles for evaluating the perception quality of coding of audio codecs. The results of subjective listening test are shown ingure 8.

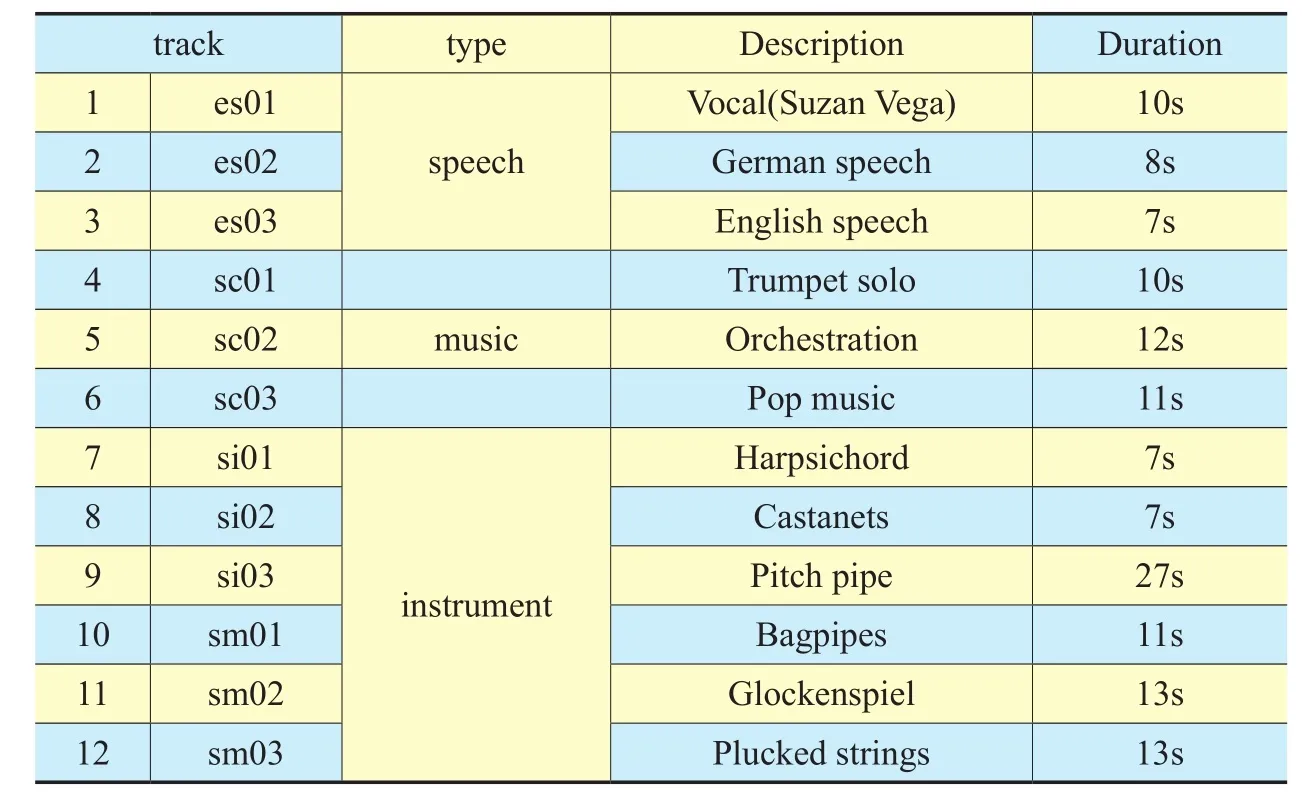
Table II. List of test material in our experiments.

For the selected reference codecs, the CMOS of our method is more than 0.15 except the USAC, which indicates a signicant improvement using DBLSTM- RNNs instead of conventional replication method. And we alsond the CMOS is higher on codecs with the low bitrate. The average CMOS reaches 0.29 on WB+ codec (only 0.8kbps for BWE),which demonstrates the accuracy of coarse HF signal is important for perception quality of coding. For USAC, the improved potential is limited with less than 0.1 average CMOS.In USAC, a strategy of increasing bitrate for BWE is used to remedy the flaw of spectral band replication. The purpose, DAE is selected as reference codec, is to verify the contribution of context dependent LF signal compare with the current frame LF. From the CMOS ingure 8, the score reaches 0.18, a signication improvement is showed, and which illustrates the correlation indeed exists in the successive frame besides the present time frame.

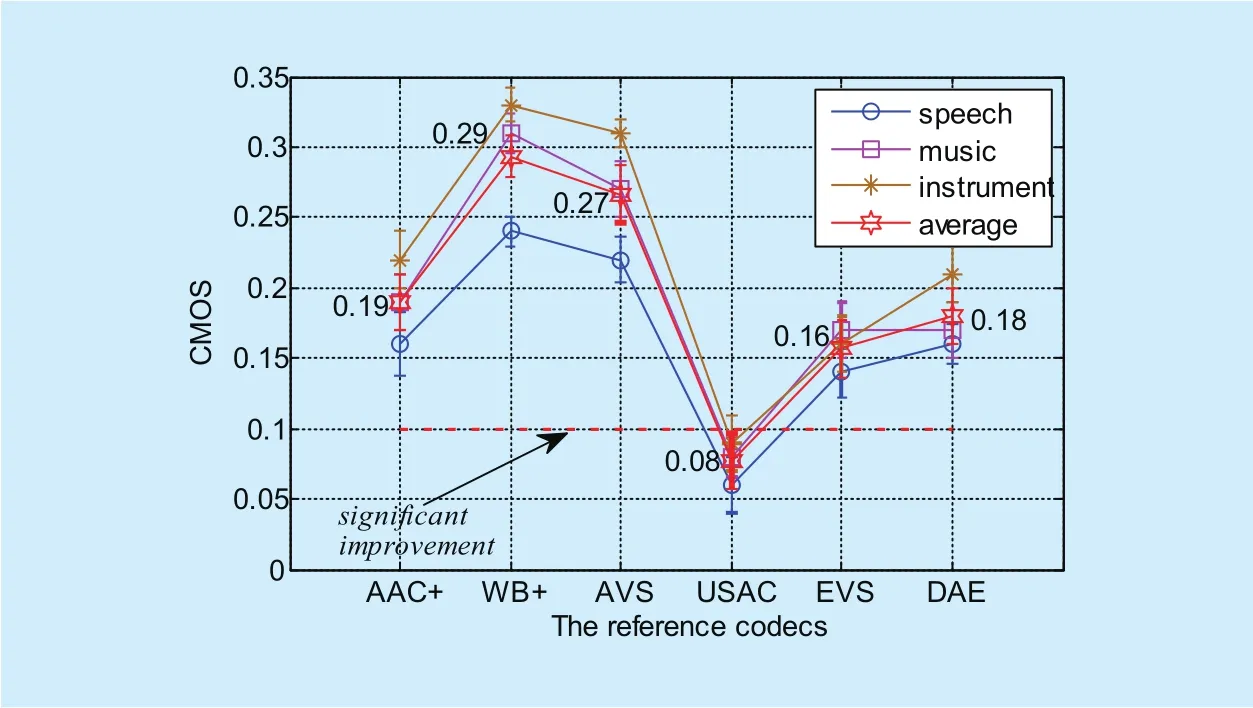
Fig. 8. Comparison mean opinion scores (CMOS) of quality comparisons between different reference codecs in the CCR test. The scores for various audio types are shown separately. Error bars indicate the standard error of the mean.

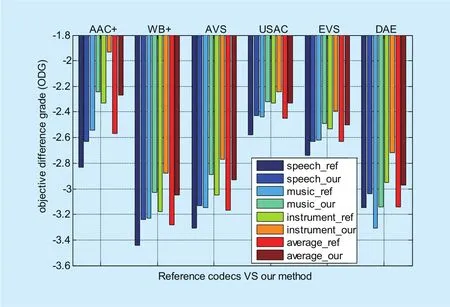
Fig. 9. Objective difference grade (ODG) of quality comparisons between different reference codecs and our method in the PEAQ test. The scores for various audio types are shown separately.

For various audio types (speech, music,instrument), the CMOS of our method appears an obvious discrimination. For speech test samples, the CMOS is the lowest, while the highest CMOS appears on instrument test samples. This phenomenon can be explained according to the frequency components of signal. For speech and instrument signals,the richness of the harmonic is different on HF bands, and the instrument is richer than speech. The richer harmonic will bring about the stronger correlation between LF and HF.Therefore, the performance of DBLSTMRNNs can be better for the case of rich harmonic signal.

4.4 Objective evaluation

In order to further evaluate the performance of the proposed method, we also implement an objective test using the perceptual evaluation of audio quality method (PEAQ) [39]. PEAQ,as ITU-R Recommendation BS.1387, is a standardized algorithm for objectively measuring perceived audio quality. A PQevalAudio test software tool [40] is used to evaluate the objective difference grade (ODG) between reference sample and test sample, the ODG values range from 0 to -4, where 0 corresponds to an imperceptible impairment and –4 to an impairment judged as very annoying. In order to match the subjective test, we used the same test material as the subjective test (see Table 2).

The objective test results are shown ingure 9, as expected, the ODG are approximately consistent with the CMOS of subjective listening test. The average ODG increased by 15.39%, 22.76%, 17.05%, 7.45%, 11.84%,13.55% on AAC+, WB+, AVS, USAC, EVS,DAE, respectively, and the total average ODG increased by 14.67%. The objective test results are also further verify the better performance of the proposed method compare with the reference codecs.

4.5 Computational complexity

In order to assess the calculation complexity, a simple codec runtime is executed. A 368 seconds wavele is selected as test item, and the run environment of test is also same between different codecs. Taking account into the implement location of our method on codecs,the test is carried out on the decoder side. We used a GetTickCount function at Visual C++(windows.h) to capture the runtimes, including whole decoder of reference codecs and our method, single DBLSTM- RNNs module. In order to reduce the runtimes, the parameters of network are stored to memory instead ofle. All test programme is implemented on Inter(R) Core(TM) i3- 2370M CPU @2.40 GHz,4G memory, Windows 7.0 OS. The runtimes of each codec are listed in Table 3.

The runtimes of our method are inevitably incremental because of its complex architecture of network. The average runtimes of decode increased by 42.64% using our method to predict the coarse HF signal. And the runtimes of RNNs module accounts for 40.25% of total decode procedure. Despite having expensive computation complexity, our method is still acceptable on some non-real-time application scenario.

V. CONCLUSION

A method for the prediction of the coarse HF signal in non-blind bandwidth extension was described in this paper. The method was found to outperform the reference method for bandwidth extension both in subjective and objective comparisons. According to the testing results, the performance was excellent for the low bitrate BWE, and the outstanding prediction capacity was emergent for the rich harmonic signal, like as instruments. In addition to improving the perception quality of coding,we also found that the context dependent LF signal was vital for generating more accurate HF signal.

Though the proposed method has a superior performance, the expensive computation complexity will limit its application, e.g. real-time application scenario. Consequently, reducing the computation complexity is still required in future work. Moreover, the perception quality of coding on USAC codec was satisfactory,while the bitrate is still high (3.5kbps) for BWE. Reducing the redundant parameters of HF is also further work.

Table III. The runtimes comparison (unit: second).

ACKNOWLEDGEMENT

We gratefully acknowledge anonymous reviewers who read drafts and made many helpful suggestions. This work is supported by the National Natural Science Founda

tion of China under Grant No. 61762005,61231015, 61671335, 61702472, 61701194,61761044, 61471271; National High Technology Research and Development Program of China (863 Program) under Grant No.2015AA016306; Hubei Province Technological Innovation Major Project under Grant No.2016AAA015; the Science Project of Education Department of Jiangxi Province under No. GJJ150585. The Opening Project of Collaborative Innovation Center for Economics Crime Investigation and Prevention Technology, Jiangxi Province, under Grant No. JXJZXTCX-025;

[1] Larsen, Erik R, and R. M. Aarts.Audio Bandwidth Extension: Application of Psychoacoustics, Signal Processing and Loudspeaker Design.John Wiley& Sons, 2004.

[2] T. D. Rossing, F. R. Moore, and P. A. Wheeler.The science of sound. Addison Wesley, 3rd edition,2001.

[3] Arttu Laaksonen. “Bandwidth extension in high-quality audio coding”.Helsinki University of Technology, 2005.

[4] M Dietz, L Liljeryd, K Kjörling, O Kunz. “Spectral Band Replication, a novel approach in audio coding“.Proc. 112th AES, 2002, pp. 1-8.

[5] J. Makinen, B. Bessette, S. Bruhn, P. Ojala. “AMRWB+: a new audio coding standard for 3rd gen-eration mobile audio services”.Proc. ICASSP,2005, pp. 1109-1112.

[6] Geiser B, Jax P, Vary P, et al. “Bandwidth Extension for Hierarchical Speech and Audio Coding in ITU-T Rec. G.729.1“.IEEE Transactions on Audio Speech & Language Processing, vol.15, no.8,2007, pp. 2496-2509.

[7] Zhang T, Liu C T, Quan H J. “AVS-M Audio: Algorithm and Implementation”.EURASIP Journal on Advances in Signal Processing, vol.1, no.1, 2011,pp. 1-16.

[8] GB/T 20090.10-2013.Information technology advanced audio and video coding Part 10: mobile speech and audio. 2014 (in Chinese).

[9] Quackenbush S. “MPEG Unified Speech and Audio Coding”.IEEE Multimedia, vol. 20, no. 2,2013, pp. 72-78.

[10] Bruhn, S., et al. “Standardization of the new 3GPP EVS codec”.Proc. ICASSP,2005, pp. 19-24.

[11] A.H. Nour-Eldin and P. Kabal. “Mel-frequency cepstral coeffcient-based bandwidth extension of narrowband speech”.Proc. INTERSPEECH,2008, pp. 53-56.

[12] Seltzer, Michael L., Alex Acero, and Jasha Droppo. “Robust bandwidth extension of noise-corrupted narrowband speech”.Proc. INTERSPEECH,2005, pp. 1509-1512.

[13] Chennoukh, S., et al. “Speech enhancement via frequency bandwidth extension using line spectral frequencies”.Proc. ICASSP, 2001, pp. 665-668.

[14] Hang B, Hu R M, Li X, et al. “A Low Bit Rate Audio Bandwidth Extension Method for Mobile Communication”.Proc. PCM, 2008, pp. 778-781.

[15] Wang Y, Zhao S, Mohammed K, et al. “Superwideband extension for AMR-WB using conditional codebooks”.Proc. ICASSP,2014, pp.3695-3698.

[16] V Atti，V Krishnan，D Dewasurendra，V Chebiyyam, et al. “Super-wideband bandwidth extension for speech in the 3GPP EVS codec”.Proc. ICASSP, 2015, pp. 5927-5931.

[17] Nagel F, Disch S. “A harmonic bandwidth extension method for audio codecs”.Proc. ICASSP,2009, pp. 145-148.

[18] Nagel F, Disch S, Wilde S. “A continuous modulated single sideband bandwidth extension”.Proc. ICASSP, 2010, pp. 357 -360.

[19] Zhong H, Villemoes L, Ekstrand P, et al. “QMF Based Harmonic Spectral Band Replication”.Proc. 131st AES, 2011, pp. 1-10.

[20] Neukam C, Nagel F, Schuller G, et al. “A MDCT based harmonic spectral bandwidth extension method”.Proc. ICASSP, 2013, pp. 566-570.

[21] Liu C M, Hsu H W, Lee W C. “Compression Artifacts in Perceptual Audio Coding”.IEEE Transactions on Audio Speech & Language Processing,vol. 16, no. 4, 2008, pp. 681-695.

[22] Krishnan V, Rajendran V, Kandhadai A, et al.“EVRC-Wideband: The New 3GPP2 Wideband Vocoder Standard”.Proc. ICASSP,2007, pp. 333-336.

[23] Sverrisson S, Bruhn S, Grancharov V. “Excitation signal bandwidth extension”, USA, US8856011,2014.

[24] Zölzer U. “Digital Audio Signal Processing (Second Edition)“. Wiley, 2008.

[25] Nour-Eldin A H, Shabestary T Z, Kabal P. “The Eect of Memory Inclusion on Mutual Information Between Speech Frequency Bands”.Proc.ICASSP,2006, pp. 53- 56.

[26] Mattias Nilsson and Bastiaan Kleijn, “Mutual Information and the Speech Signal”.Proc. INTERSPEECH, 2007, pp. 502-505.

[27] T. M. Cover and J. A. Thomas, “Elements of Information Theory”. Wiley, 1991.

[28] Liu H J, Bao C C, Liu X. “Spectral envelope estimation used for audio bandwidth extension based on RBF neural network”.Proc. ICASSP,2013, pp. 543-547.

[29] Liu X, Bao C. “Audio bandwidth extension based on ensemble echo state networks with temporal evolution”.IEEE/ACM Transactions on Audio Speech & Language Processing, vol. 24, no. 3,2016, pp. 594-607.

[30] WANG Yingxue, ZHAO Shenghui, YU Yingying,KUANG Jingming. “Speech Bandwidth Extension Based on Restricted Boltzmann Machines”.Journal of Electronics & Information Technology,vol. 38, no. 7, 2016, pp. 1717-1723.

[31] Jiang L, Hu R, Wang X, et al. “Low Bitrates Audio Bandwidth Extension Using a Deep Auto-Encoder”.Proc. PCM, 2015, pp. 528-537.

[32] H Sak，A Senior，and F Beaufays. “Long shortterm memory recurrent neural network architectures for large scale acoustic modelling”,Proc. INTERSPEECH. 2014, pp. 338- 342.

[33] Williams RJ, Zipser D. “A learning algorithm for continually running fully recurrent neural networks”.Neural Computation, vol. 1, no. 2, 1989,pp. 270–280.

[34] Hochreiter S, Schmidhuber J. “Long short-term memory“.Neural Computation, vol. 9, no. 8,1997, pp. 1735–1780.

[35] Oord A V D, Dieleman S, Zen H, et al. “WaveNet:A Generative Model for Raw Audio”. 2016. URL https://arxiv.org/ abs/1609.03499.

[36] Herre J, Dietz M. “MPEG-4 high-effciency AAC coding”.IEEE Signal Processing Magazine, vol.25, no. 3, pp. 137- 142.

[37] “High performance computing system of Wuhan University”. http://csgrid.whu.edu.cn/ (in Chinese).

[38] “ITU-T: Methods for Subjective Determination of Transmission Quality. Rec. P.800”. International Telecommunication, 1996.

[39] Thiede T., Treurniet W. C., Bitto R. et al. “PEAQ---The ITU Standard for Objective Measurement of Perceived Audio Quality”.Journal of the Audio Engineering Society, vol. 48, no. 1, 2000, pp.3-29.

[40] McGill University, “Perceptual Evaluation of Audio Quality”. http://www.mmsp.ece.mcgill.ca/Documents/Software

[41] Miao L, Liu Z, Zhang X, et al. “A novel frequency domain BWE with relaxed synchronization and associated BWE switching”,Proc. GlobalSIP,2015, pp.642-646.

[42] Helmrich C R, Niedermeier A, Disch S, et al.“Spectral envelope reconstruction via IGF for audio transform coding”.Proc. ICASSP, 2015, pp.389-393.

[43] Vapnik, Vladimir N. The Nature of Statistical Learning Theory. Springer, 1995.

[44] LI Hong-rui, BAO Chang-chun, LIU Xin, et.al.Blind Bandwidth Extension of Audio Based on Fractal Theory. Journal of Signal Processing. Vol.29, no. 9, 2013, pp. 1127- 1133. (in Chinese)

[45] Chinese AVS Workgroup, M1628: The specification of subjective listening test for AVS audio technology proposal. AVS Audio group special sessions. August 15, 2005, Wuhan China. (in Chinese)