基于正弦逼近算法的电网故障快速识别方法

(重庆电力高等专科学校，重庆 400053)

现代化工厂供电容量不断增大，对连续可靠供电的要求越来越严格。供电系统的任何异常都会影响其正常生产、运营，甚至会导致全系统停电。当供配电网发生故障，需要快速识别故障类型，针对三相短路、两相短路、单相接地短路及两相接地短路等不同故障类型，采取不同的处理方式。利用正弦逼近算法，提取不同类型故障时，根据三相电压幅值的不同特征，用模式识别技术对故障类型进行快速识别，可缩短故障处理时间，提高故障处理效率，从而提高供电可靠性。

1 正弦逼近算法提取故障电压幅值

1.1 基本原理

电网发生故障后，电压幅值和相位会随时间t而变化，其瞬时值用式(1)表示为

u(t)=Um(t)sin[ωt+θ(t)]

(1)

对电压每隔Ts采样得到一个离散时间序列，它的第n个元素(位于t=nT)是

x[n]=Um(nT)sin[ωnT+θ(nT)]

(2)

(3)

定义列向量为

Y=(x[1]，x[2]，…，x[M])T

(4)

正弦逼近的目的是从式(2)中提取出2个离散时间序列y[n]=Um(nT)和z[n]=θ(nT)。

若将式(3)改写为

(5)

则

(6)

(7)

只要求出A[n]和B[n]，则得到x[n]，y[n]和z[n]。用2个N阶最小二乘多项式来分别拟合A[n]和B[n]的数据，则

(8)

(9)

式中：u，v为多项式系数。

(10)

误差定义为

(11)

当

(12)

W=(u0，u1，…，uN，v0，v1，…，vN)T

(13)

再构建一个M×2(N+1)的矩阵X，矩阵各元素为

(14)

i=1，2，3，……，M

j=1，2，3，……，2(N+1)

矩阵X和W相乘得到如下形式的列向量

(15)

结合式(5)，式(12)，式(13)和式(15)可得

(16)

设W的初值为W0，给定一极小的正数ε，用“牛顿-拉弗逊”法求W中各元素u，v的值，再将u，v代入式(8)和式(9)，则得到A[n]和B[n]，将估算值带入式(6)和式(7)，最终可得到故障电压幅值和相位值。

2 算例分析

2.1 初始条件设置

本文采样时间间隔T=0.25 ms，一个周期的正弦样本数为M=20 ms/0.25 ms=80，5 ms内样本数为L=20，最小二乘多项式阶数为5，先计算矩阵X各元素：

(17)

取W的初值W0为

W=(1，0，0，0，0，0，0，0，0，0，0，1，0，0，0，0，0，0，0，0，0，0)T

(18)

2.2 求解非线性方程组

采样值Y=(x[1]，x[2]，x[3]，…，x[20])T已知，可按照以下流程求解W

ΔW=-2[X×Y-X×(X′×W0)]

W=W0-μΔW，其中迭代步长μ=0.005

ΔJ=‖Y-X′×W‖

若ΔJ<ε(ε=0.01)，则迭代结束。

2.3 提取幅值和相位

(19)

(20)

(22)

3 计算结果分析

图1为失电后20 ms内A相电压变化情况，线条是采样数据，曲线1是逼近值，曲线2是幅值。

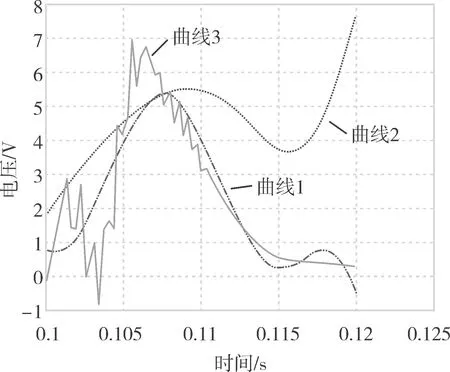
图1 失电后20 ms内正弦逼近效果

从图1可看出，逼近值与采样数据趋势基本一致，采用正弦逼近算法能够得到良好的计算结果。

在不同位置发生不同断电/故障，故障后5 ms内代表三相电压幅值的25个离散值构成的曲线呈现出不同形状，对所有曲线分析后发现，每条曲线最多只有一个拐点；而某些曲线是单调的，即不存在拐点。基于这一特点，可以构建一故障识别系统，系统的学习部分将各种可能出现的曲线以二进制数码形式作为样本储存到计算机中，完成样本存储；系统的识别部分将待识别的故障曲线经过编码变成二进制数码，在查阅了样本存储中的各种编码后，通过比较识别来判断它属于何种故障。

4 结论

在其他条件下的不同故障时，利用正弦逼近算法可以获得不同故障情况下三相电压幅值。发生不同类型故障时，三相电压幅值呈现出不同的特征，将该特征作为故障识别系统的样本进行存储，在机器学习样本存储中的各种编码后，可用模式识别技术对故障进行快速识别。