碎纸片自动拼接复原

廖敏瑜，谢睿诚，余声宇

（汕头大学理学院数学系，广东 汕头 515063）

0 引言

破碎文件的拼接在司法物证复原、历史文献修复以及军事情报获取等领域都有着重要的应用.传统上，拼接复原工作过分依赖人为干涉，当碎片数量巨大，内容复杂时，不但耗费大量的时间及人力，还可能对纸张信息造成损害.若纸张信息隐秘，还可能人为泄密造成不可估量的危害.因此，全自动拼接碎纸片的技术是十分必要的.

文献[1]和文献[2]研究了通过碎中文纸片内的文字行特征和表格特征来进行拼接，这种方法提高了拼接效率和降低了拼接难度，但是仍需要较多的人工干预进行拼接.文献[3]研究的算法正确率高，但是仅适用于中文碎纸片的拼接不适用于英文碎纸片的拼接.文献[4]是研究英文碎纸片的拼接，但是其掺杂了较多人工干预，而且各操作之间的连带作用强，即前面操作错误就会导致后面的错误.文献[5]通过聚类将碎纸片进行行分类，能够不受人工干预就实现碎纸片的拼接，这种方法能够将字母行位置相差明显的碎纸片进行聚类，但是却不能将字母行位置相差较小乃至无差距的碎纸片进行聚类，因此不能普遍解决碎纸片拼接问题.文献[6]研究双面英文碎纸片的拼接，提出一种运用聚类分析、MATLAB搜索算法和人工干预等相结合的方法，但其加入太多的人为干预.

为了得到无人工干预且适用性广的碎纸片拼接方案，本文提出一种基于改进的遗传算法（GA）及光学字符识别技术（OCR）的自动化拼接算法.针对英文文档，通过研究碎纸片英文字母所在行的几何特征信息及消除同行字母高度不同的干扰，对碎纸片进行分类；该分类是通过英文字母所在标准四格线的中部下基线的位置来构建的.将分类后的碎纸片间的拼接问题转化为旅行商问题，采用改进的GA算法和OCR技术处理问题.通过字母中部下基线的位置及以贪婪算法为辅，处理组行成页的问题.最后，本文还将对英文碎纸片拼接的方案推广，结合中文文字的特点，将算法改装为能够处理中文碎纸片拼接问题.

本文采用2013年全国大学生数学建模竞赛B题[8]209个英文碎纸片和209个中文碎纸片图像（分别由一个A4大小的英文文档碎纸片经横纵切成11×19，大小都为row×col的规则碎纸片）作为仿真数据.

1 英文碎纸片拼接原理

1.1 文档分类

通过观察，英文字母与中文汉字具有不同的结构特征.在中文文档中，同行文字的高度基本一致，而英文文档中，同行英文字母高度一般不统一.将印刷字母放置于四线格上，可将其分为四线格的上、中、下3部（记为上部，中部，下部）由印刷字母的特点及英文文章中各字母出现的频率统计结果可知，所有大写字母都占上中部，有9个小写字母（b，d，f，h，i，j，k，l，t）是有占上部，占比约为 28.95%，有 5 个小写字母（g，j，p，q，y）是有占下部，占比约为6.17%，所有的小写字母都有占中部.由上面的分析可知，英文字母中部能有效提供行分类的信息，而上下部则会对行分类产生干扰，且下部对行分类的干扰较少.为此，记英文字母中部和下部之间的分界线为下基线，如图1所示.

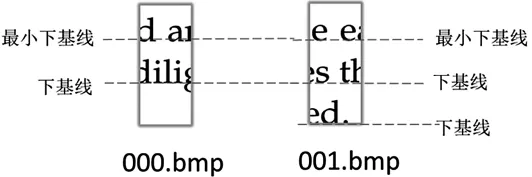
图1 英文基线位置

如果碎纸片处于同一行中，则它们的部分下基线的位置基本相同.本文将最小下基线位置基本相同的碎纸片归为一类，得到的类别有两种情形：

（1）单行混合：当一行碎纸片的最小下基线与其他行的区别较大时，可将这一行碎纸片可归为一类，得到单行混合的情况.

（2）多行混合：当一行碎纸片的最小下基线与其他部分行的区别较小乃至没有区别时，可将其归为一类，得到多行混合的情况.

1.2 行首和行尾的确定

分类后，每一类碎纸片中行首和行尾碎纸片个数与其组合行数一样.由于文档存在页边距，如图2所示，所以本文通过处于行首碎纸片的左端和处于行尾碎纸片的右端存在较多空白，分别确定处于行首和行尾的碎纸片.

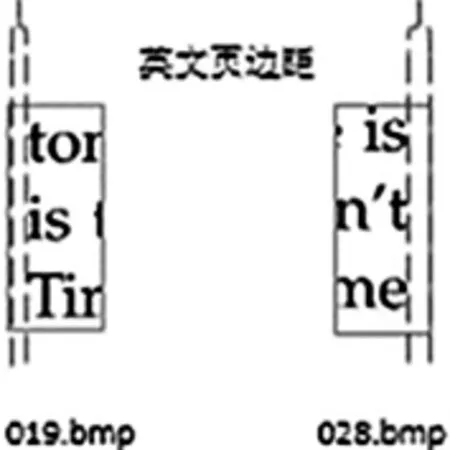
图2 边界位置

1.3 行内拼接

由于各碎纸片的纵向长度较小，如果依次匹配边界不匹配距离最小的碎纸片，会造成很大的偏差.根据文献[3]，本文类比旅行商问题设计问题：将各个碎纸片作为访问点，定义碎纸片之间的距离，从行首碎纸片出发，经过其它碎纸片各一次，最后回到行尾碎纸片.将行内碎纸片的最佳排列问题转化为相应的旅行商问题的最优解.

针对1.1的情形（1）中碎纸片的拼接：由于访问点个数较少，将行首碎纸片和行尾碎纸片分别固定在第一个位置和最后一个位置，将寻找全局最小的不匹配问题转化为旅行商问题，运用改进的遗传算法进行求解.

针对1.1的情形（2）中碎纸片的拼接：由于访问点个数是情形（1）的碎纸片个数的至少两倍，如果直接采用遗传算法进行求解会造成很大的偏差.为了减少计算复杂度并得到最优解，本文将旅行商问题进行推广，不仅采用遗传算法先求初步求解，还设计了一种光学字符识别（OCR）技术检验初步解的拼接情况.以两行混合成类的碎纸片拼接为例，这两行碎纸片分别含有两个行首碎纸片（记为行首1，行首2）和两个行尾碎纸片（记为行尾1，行尾2）.在第1，19，20，38位置依次固定行首1，行尾1，行首2及行尾2碎纸片（或行首1，行尾2，行首2及行尾1碎纸片），共有2种组合.我们对这两种组合用改进的遗传算法迭代一定的次数，然后挑选出迭代后距离较短的一种情况保留下来，作为初始拼接情况.采用OCR技术筛选初始拼接的状况，再次用遗传算法对拼接错误处进行求解.

1.4 组行成页

当文档完成所有行内拼接后，每行碎纸片看成一个新的碎纸条，先通过上端和下端较多的空白来确定行首碎纸条和行尾碎纸条.根据上下两个碎纸条的下基线间的高度基本为间距行高和四线格高度之和的整数倍这一准则，得到碎纸条的排列，完成碎纸片的拼接.

2 碎纸片的拼接算法

2.1 图像预处理

将碎纸片图像转化为灰度值矩阵A（k），k＝1，2，…，209，由于文字的边缘轮廓是灰色的，避免这部分元素对确定行距高度等产生干扰，运用公式（1）对A（k）的元素进行二值化处理得到，那么由构成的矩阵B（k）的元素仅为0和1，即碎纸片图像仅含黑白二色.

2.2 文档分类

先寻找碎纸片的下基线，从而实现文档分类，具体步骤如下：Step1：设一个维度为row的列向量α（k）的第i个元素值是大小为row×col的二值矩阵B（k）第i行中经过的墨迹数，其计算如公式（2）所示

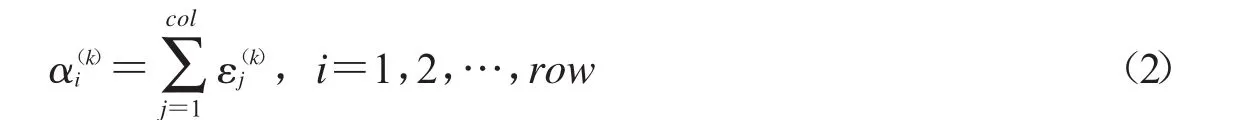
其中

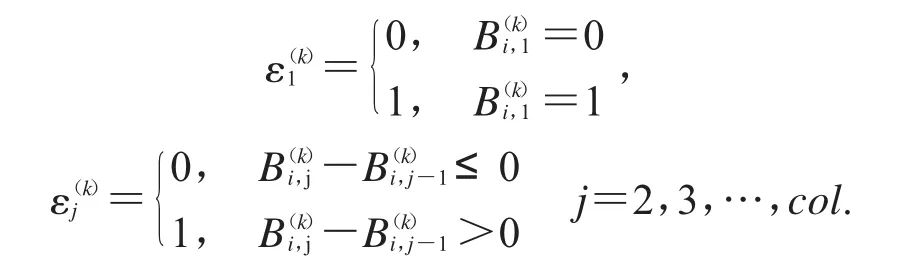
Step2：设一个维度为row的列向量β（k）的第i个元素为C（k）的第i个元素的等级划分，如图3所示，其计算如公式（3）所示

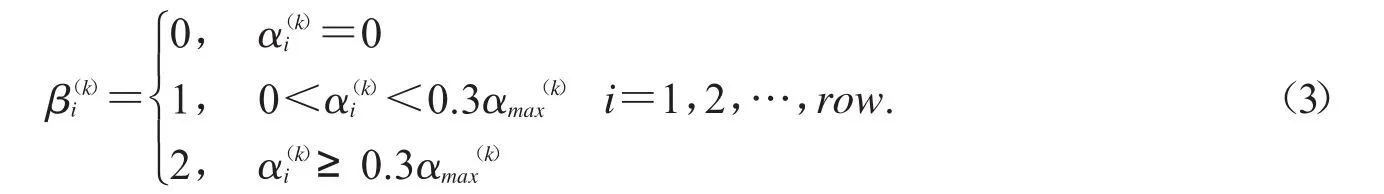
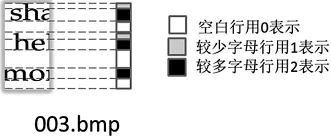
图3 像素等级划分

Step3：记四格线的上、中、下部和间距的像素点高度分别为highup，highmid，highlow和highgap.利用游程思想，计算出β（k），k＝1，2，…，209的局部分量全为 0，全为 1，全为 2的长度，再取各长度的众数分别作为highgap，highup（highlow）和highmid的值.四格线高度及间距高度之和记为hightotal，其计算如公式（4）所示

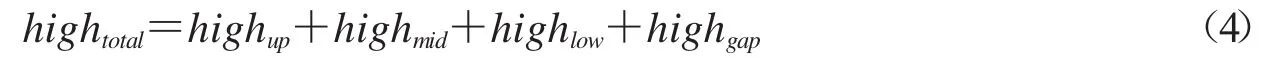
Step4：从上往下搜索β（k）向量，直到其局部向量元素全为2且长度至少为highmid判断出其表示中部，取其下界作为下基线的位置base（k）.针对少部分β（k）向量没有局部向量元素全为2且长度至少为highmid的情况，同样从上往下搜索β（k）向量，直到其局部分量全为1且长度至少为highmid，若其长度近似为highmid，取其下界作为下基线的位置base（k）；若其长度近似为highmid＋highup且其上部分比下部分的值小，取其下界作为下基线的位置base（k）；若其长度近似为highmid＋highup且其下部分比上部分的值小，取其highmid对应的位置作为下基线的位置base（k）；记最小下基线的位置为base（k）min，其计算如公式（5）所示

Step5：利用同行碎纸片下基线基本相同的原理及每一行固定的碎纸片数目的整数倍进行分类.例如，下基线位置为19的碎纸片个数为18，而位置为20的碎纸片个数为1，则它们处于同一类；下基线位置为40的碎纸片个数为17，位置为41的碎纸片个数为19，位置为42的碎纸片个数为2，则它们处于同一类.

2.3 行首和行尾的确定

根据页边距寻找出行首和行尾碎纸片，具体步骤如下：

Step1：设一个维度为col的行向量γ（k）的第j个元素为大小为row×col的二值矩阵B（k）第j列有无墨迹的情况，其计算如公式（6）所示

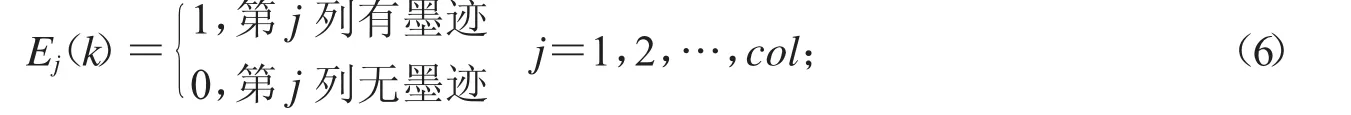
Step2：先确定每一类中碎纸片的行数n，然后挑选出E（k）左端向量0元素最多的n个碎纸片作为行首碎纸片，挑选出E（k）右端向量0元素最多的n个碎纸片最为行尾碎纸片.

2.4 行内拼接

2.4.1 碎纸片之间的距离

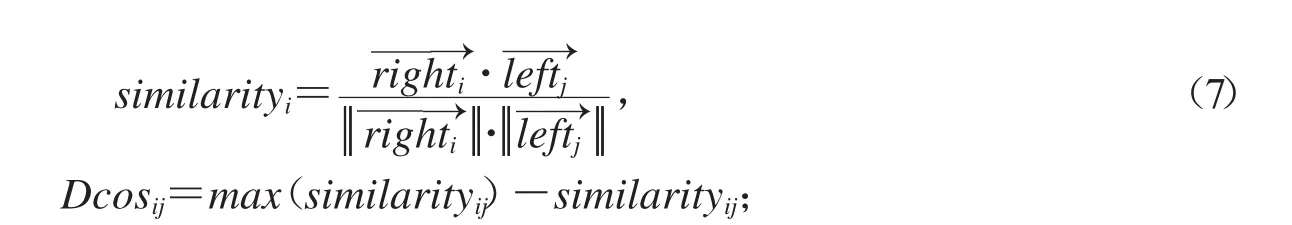
记第i个碎纸片和第j个碎纸片之间的有向不匹配距离为Dmisij，其计算如式（8）所示：

2.4.2 改进遗传算法（GA）

遗传算法是一种求解最短路的算法，为了使之能够处理碎纸片拼接转化为的旅行商问题，基于文献[8]，本文对传统的遗传算法的交叉，变异，内部交换中做了改进，改进的如下：

1）交叉操作

采用部分映射杂交，确定交叉操作的父代，将父代样本两两分组，每组重复以下过程（方便起见假定单行碎片数为10）：

a.产生两个随机整数r1，r2∈[2，9]确定两个位置，对两个位置间中间元素进行交叉，如 r1＝4，r2＝7：

交叉为：

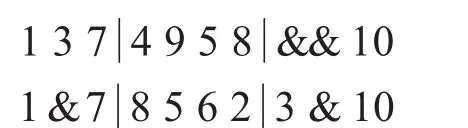
b.交叉后同一条染色体中有重复碎片编号的，不重复的编号进行保留，有冲突的数字（&位置）采用部分映射来消除冲突，即利用中间段的对应关系进行映射，结果为：

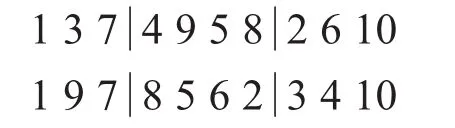
2）变异操作

变异操作采取随机选取r1，r2∈[2，9]中的两个位置，将其中的元素对换.如随机选取位点 r1＝4，r2＝7：

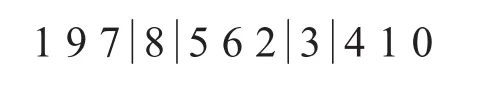
变异后为：

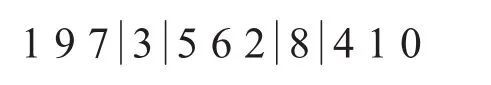
3）内部交换操作

随机选取 r1，r2，r3∈[2，9]，3个位点，将r1与 r2之间的元素和 r2与 r3之间的元素对换，例如随机选取 r1＝2，r2＝5，r3＝8：

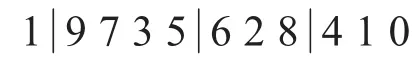
内部交换后的结果为：

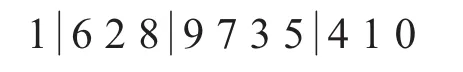
2.4.3 光学字符识别（OCR）

光学字符识别是一种能够识别出图像文本内容的技术.为了减少计算复杂度并得到最优解，本文自制OCR技术检验拼接口处字母是否完整正确，从而判断碎纸片是否拼接正确.实现OCR技术的步骤如下：

1）制作字典

首先对文字进行自动化切割.切割时采用先横切，后纵切，再横切去除空白的流程进行操作，使得每个字母都处于最小的矩形中，一个切割的例子如图4所示.切割获取现有的完整字母，提取不同字母制成字典.为了减少计算复杂度并得到最优解，引入光学字符识别（OCR）技术来对连接处的正确状况进行判断.

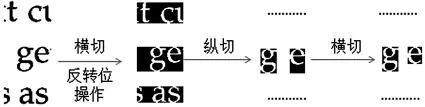
图4 文字切割流程

2）建立模型

由于切割后即便相同的字母也并不完全相同，所以考虑字母图像像素点的净相似率f1和形状相似度f2，其计算分别如公式（9），（10）所示：

其中d为切割后字母的像素点宽度，h为像素点高度，p为墨迹像素点总个数.假设拼接处有三行文字，设iscorrect表示是否通过OCR检验的检验量，则评价规则为：

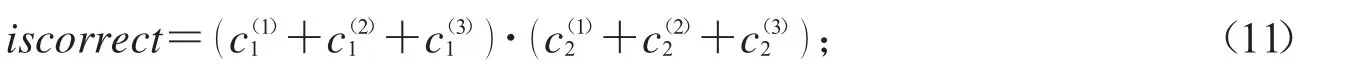
当iscorrect＞0时，通过检验，则判断拼接处正确；

当iscorrect＝0时，不通过检验，则判断拼接处错误.

2.4.4 针对一行碎纸片混合的拼接

针对一行碎纸片混合的拼接问题，本文将其转化为旅行商问题，然后采用遗传算法求解.在改进的遗传算法中，固定第一个位置为行首碎纸片，最后一个为行尾碎纸片.由于不匹配距离收敛速率比余弦距离收敛速率大，因此采用不匹配距离作为遗传算法中的距离，迭代300次，寻找余下碎纸片的全局最优排列.

2.4.5 针对两行以上碎纸片混合的拼接

针对多行碎纸片混合的拼接问题，本文将其转化为广义上的旅行商问题，不但固定第一个（行首）和最后一个纸片（行尾），还在中间固定余下的行首和行尾.然后采用改进的遗传算法先求初始解，再用OCR技术检验拼接处，将不通过的拼接处再次切开，再以余弦距离为遗传算法中的距离进行迭代得到最终的结果.

在本例中针对两行混合的碎纸片，需要拼接的纸片一行有38个碎片，因此我们固定的为第1，19，20，38号位置.在两行混合的纸片中，行首和行尾共有2种组合，本文分别使用两种组合进行拼接，分别迭代5000次后，最后选取距离最小的组合保留下来作为初步解.本文再采用OCR技术检验出初步解的情况，把认为错误处再切割开并将认为正确的连接合并成块，例如图5所示.再采用遗传算法，以余弦距离作为距离迭代50次，得到最终解.

图5 OCR结果

2.5 组行成页

当文档完成所有行内拼接后，每行可看成一个新的碎纸条，通过上端和下端较多的空白来确定行首碎纸条和行尾碎纸条.

下面是排列除行首碎纸条和行尾碎纸条剩余的碎纸条的算法：

1）设第i个碎纸条的最小下基线的位置为baseline（i）min第j个碎纸条的最小下基线的位置为baseline（j）min，第j个碎纸片要与第i个碎纸片之间字母行数n的数学表达式如下：

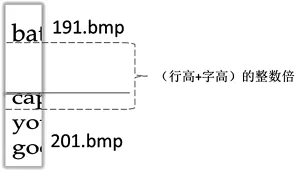
图6 基线距离

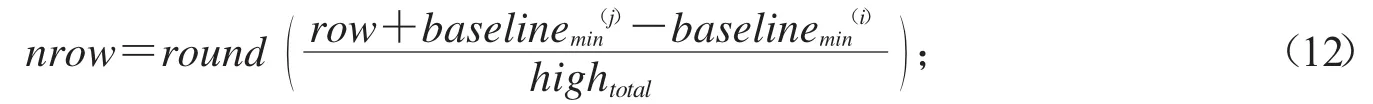
其中round表示四舍五入运算法.

2）第j个碎纸片要与第i个碎纸片匹配时，baselinej应该满足：

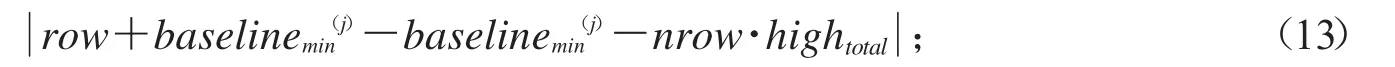
取值最小.其中row是碎纸条对应二值矩阵的行数.

3）如果满足与第i个碎纸片匹配的碎纸条j有多个时，定义gi，j为第i个碎纸条下边界和第j个碎纸条上边界的不匹配距离，即：

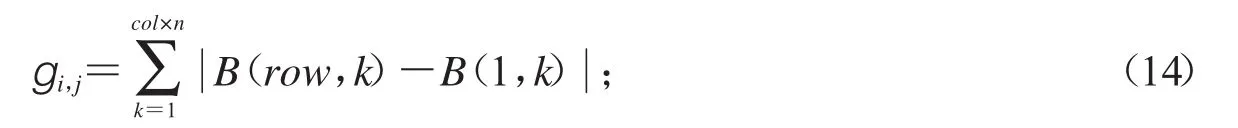
其中n为每一行碎纸片含有碎纸片的个数.

选取与第i个碎纸片不匹配距离最小的第j个碎纸片.

2.6 拼接试验

最后从拼接结果看，英文文档碎纸片在行分类时由于处于不同行的碎纸片下基线相近，所以有部分分类中含有两行碎纸片混搭的.针对这类问题，本文不仅将原来改进的遗传算法进行拓展，还设计了适用于检测边缘字母是否正常的OCR技术，来挑选拼接错误的碎纸片.由于本文设计的OCR较为严格，会将少量拼接正确的碎纸片误认为错误的，但是其能够将所有拼接错误的碎纸片寻找出来，因此不会影响拼接结果.在组行成页步骤中，由于较多是横切到行距的，所以采用贪婪算法及遗传算法都得不到好结果，所以采用基于基线的算法是行之有效的.从试验结果看，本文设计来解决英文碎纸片拼接的算法是有效的.

3 模型的推广

3.1 中文拼接

中文文字的高度基本一致，文字中间水平的线的差异较小.本文定义中心线为文字中间水平的线，如图5所示.根据同行文字的中心线基本一致，建立基于最小中心线确定碎纸片行分类的算法.再用改进的遗传算法，采用有向余弦距离，求解有中文碎纸片作为访问点的旅行商问题.在组行成页中，为了减少误差，利用中文文字的高度基本一致这一准则，把碎纸片拼接分成两种类型：

（1）针对横切到文字的碎纸条，根据上边碎纸条被切字体余下高度和下边碎纸条被切字体余下高度之和基本等于字体高度的准则，如图8所示，设第i个碎纸条最下部分黑色像素高为，第j个碎纸条最上边黑色像素高为，第i个碎纸条要与第j个碎纸条匹配时，需要满足以下式子：

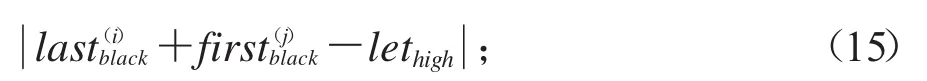
取值最小，其中lethigh表示文字像素高.

（2）针对横切到空白间隔的碎纸条，根据上边碎纸条被切空白间隔剩余的高度和下边碎纸条被切空白间隔剩余的高度之和基本等于字体高度的准则，如图9所示，设第i个碎纸条最下部分黑色像素高为last（i）white，第j个碎纸条最上边白色像素高为first（j）white，第j个碎纸条要与第i个碎纸条匹配时，first（j）white需要满足式子（16）：

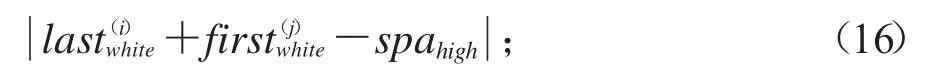
取值最小，其中spahigh表示行距像素高.

3.2 拼接试验

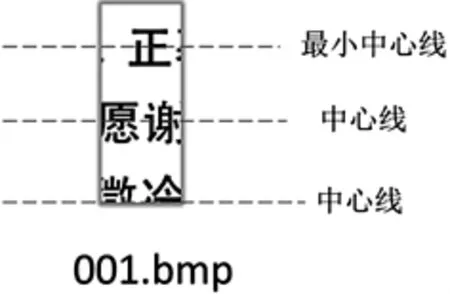
图7 中心线

图8 文字高度

图9 间距特征

由于中文文档各行碎纸片的中心线不同，所以能够实现行分类，即每一类中含每一行混合的碎纸片.本文在遗传算法中分别采用余弦距离和不匹配距离作为距离求解旅行商问题.对比发现，以不匹配距离为距离求解出来的最优解不一定是最佳解，即求解出来的最短距离经过的点的顺序对应的碎纸片序号拼接是不正确的；余弦距离作为距离求解出来的最优解是最佳解.在最后为了减少中心线间隔较远带来的误差，本文利用字高和间距基本不变的原理实现组行成页.试验结果表明，本文设计的算法针对中文文档碎纸片拼接也是有效的.

4 结语

本文消除了英文碎纸片中字母高度不同的干扰，找出了碎纸片的最小下基线，合理地利用最小下基线对碎纸片进行分类；将分类结果的拼接问题转化为旅行商问题，采用改进的遗传算法和自制的OCR技术对其进行求解；最后再次利用下基线，且以贪婪算法为辅，对碎纸条进行拼接.在文章最后进行仿真分析，采用本文提出的算法对209张英文碎纸片进行全自动拼接，无需人为干预.再结合中文文字的特点，对适用于英文碎纸片拼接的算法进行修改：在分类中采用中心线，而行内拼接中由于中文边界信息量较大所以无需OCR技术，在组行成页中利用字高及间距进行拼接得到适用于中文碎纸片拼接的算法，同样可对209张中文碎纸片进行全自动拼接，无需人为干预.本文设计的算法仅对规则碎纸片的拼接有效，对于一些不规则的碎纸片，本文还是需要对算法进行修改，这是进一步研究的问题.

致谢：感谢李健老师的悉心指导.

[1]罗智中.基于文字特征的文档碎纸片半自动拼接[J].计算机工程与应用，2012，48（5）：207-210.

[2]刘铁.基于数字图像的碎纸复原模型与算法——2013年全国大学生数学建模B题碎纸片的拼接复原问题[J].重庆理工大学学报（自然科学版），2015，27（3）：83-88.

[3]马俊明，赖楚廷，卜尚明，等.基于文字特征的规则碎纸片自动拼接[J].汕头大学学报（自然科学版），2014，29（2）：4-10.

[4]金明娅，孙丹蕾，赵艳，等.单面英文碎纸片的拼接复原及算法实现[J].延安大学学报（自然科学版），2015，34（1）：14-18.

[5]周一凡，王松静，黄永斌.英文字母特征的双面碎纸拼接[J].中国图象图形学报，2015，20（1）：85-94.

[6]张亮.基于聚类优化模型的碎纸自动拼接方法研究[J].计算机应用与软件，2015，32（12）：218-221.

[7]2013年全国大学生数学建模竞赛B题附件3和附件4的数据[EB/OL].（2013-09-13）[2017-02-25].http：//www.mcm.edu.cn/problem/2013/2013.html.

[8]郁磊，史峰，王辉，等.MATLAB智能算法30个案例分析[M].北京：北京航空航天大学出版社，2011.