Zgymund空间到Bloch空间的微分复合算子
罗志丹
(汕头大学数学系,广东 汕头,515063)
0 引言
最早关于复合算子描述的是Nordgren[1],结合解析函数与泛函分析理论,解决了Hardy空间上的相关问题.再则Cowen和MacClue刻画了复合算子在一些具体函数空间内的有界性和紧性[2].各类函数空间上的复合算子在接下来的研究中得出了一些很好的成果[3-4].
近五年来,关于复合算子的研究,着重研究其在各类函数空间上的有界性和紧性.比如与Bloch空间相关的文献[5-9];与Bergman空间相关的文献[10-12];与Zygmund空间相关的文献[13-14].
2010年,李颂孝在文献[5]中得到经典微分复合算子DCφ从Zygmund空间到Bloch空间的有界性和紧性的充要条件.我们讨论二阶微分复合算子D2Cφ,为推广到一般广义微分复合算子DmCφ作必要准备.
1 准备知识
定义微分复合算子:
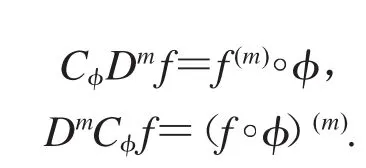
2 引理
引理2.1[14]设f属于Zygmund空间,则
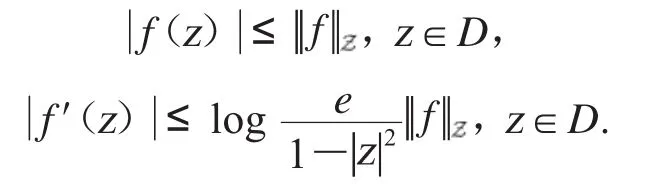
引理2.2当n≥2时,单位圆盘上的解析函数f属于Zygmund空间,则
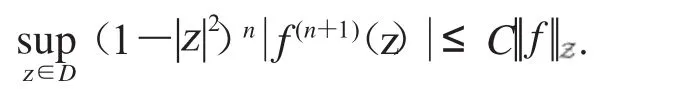
证明类似文献[4]中性质8,此处省略.
引理2.3设算子D2Cφ∶Z→B是有界算子,则D2Cφ是紧算子当且仅当对于任意的有界序列,当它在D上内闭一致收敛于0时,有
此引理为文献[15]中引理2.10特殊情形.
3 主要结果及其证明
引理3.1设φ是单位圆盘D上的解析自映射,则为有界算子的充要条件是同时满足以下三个条件
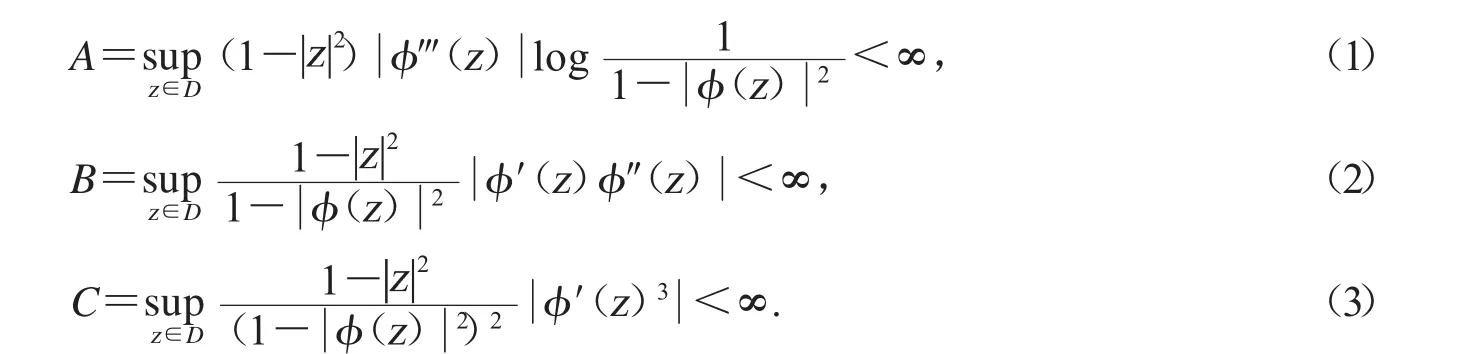
证明:充分性
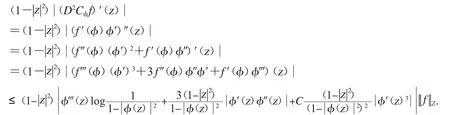
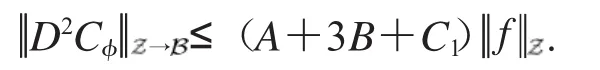
必要性
因为D2Cφ是上的有界算子,则存在常数C,使得
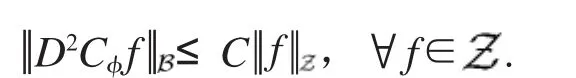
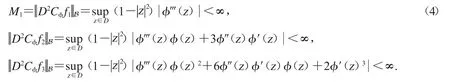
由函数φ(z)的有界性及三角不等式,可得
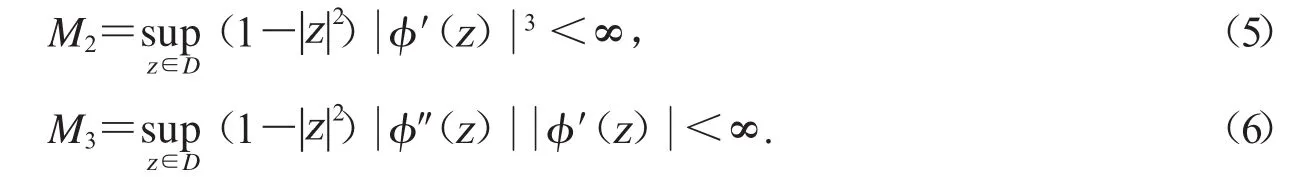
因此,
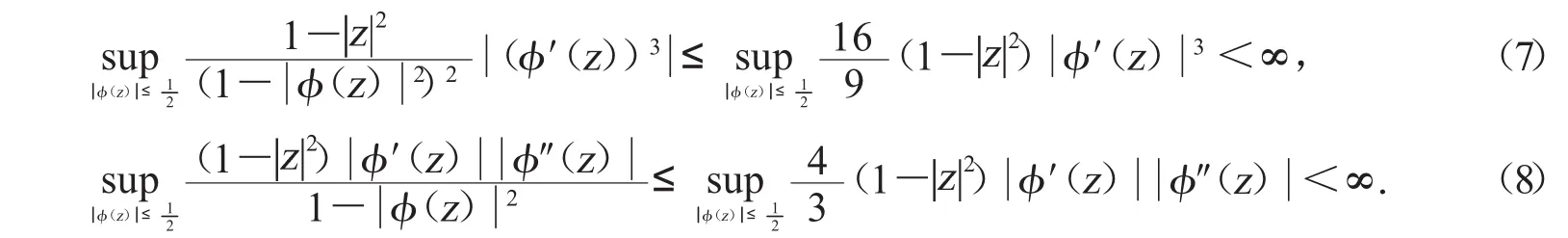
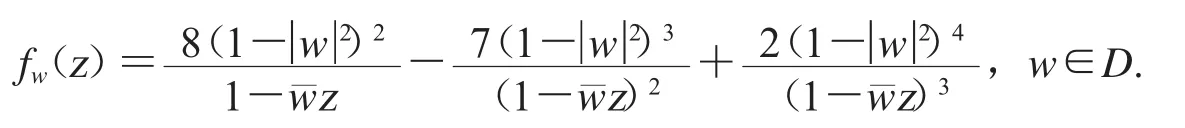
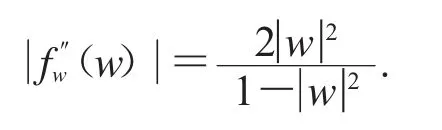
由D2Cφ的有界性,可得
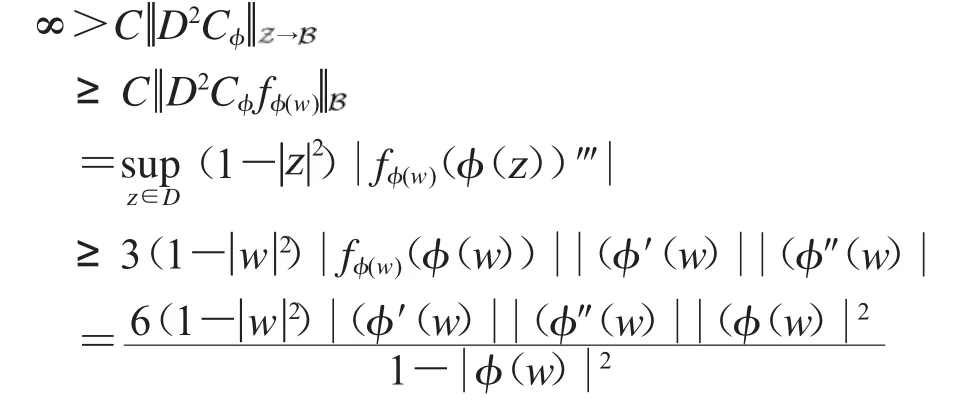
由上式,可得
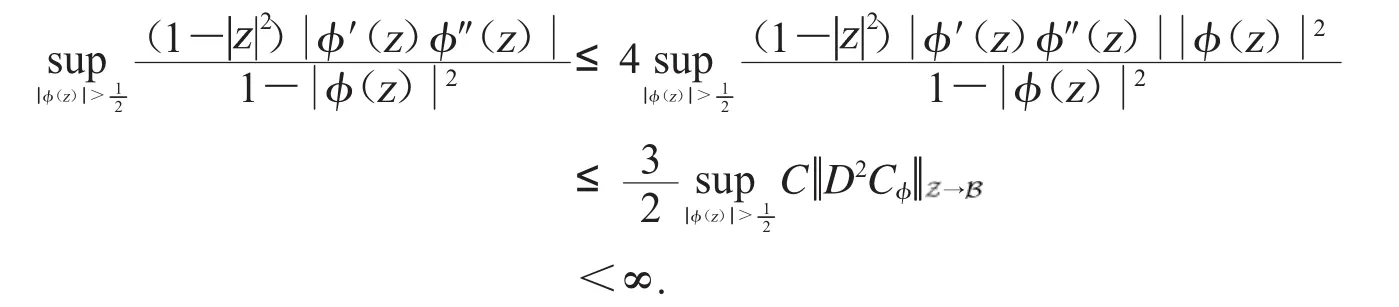
结合不等式(8),条件(2)得证.
选取函数
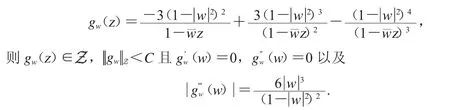
由D2Cφ的有界性,可得
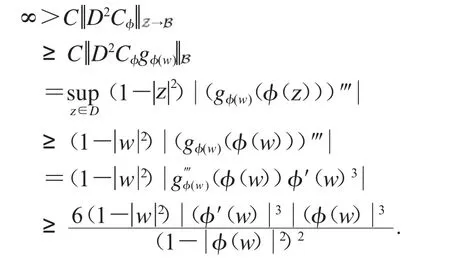
由上式得
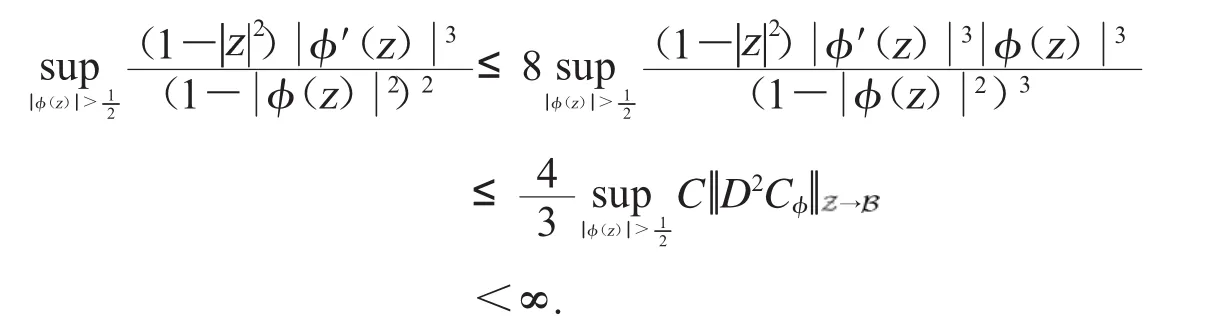
结合不等式(7),则(3)得证.
选取函数
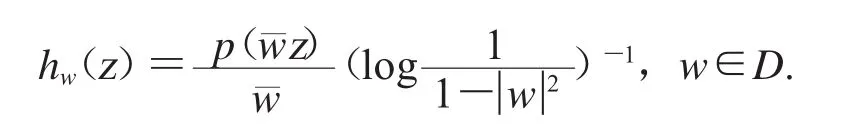
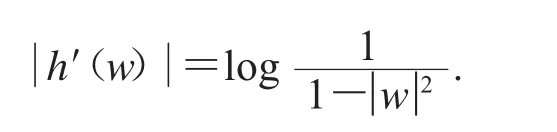
由D2Cφ的有界性,可得
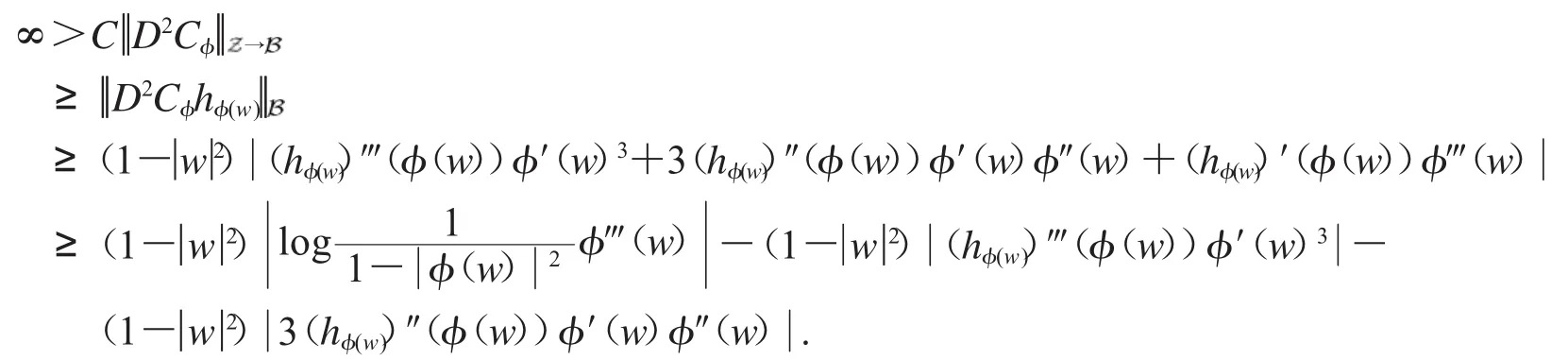
从而
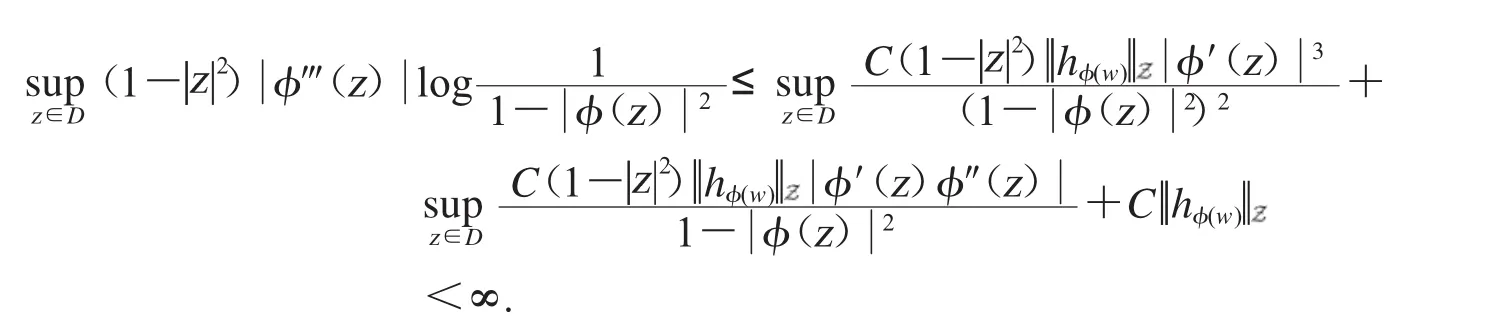
即(1)得证.
引理3.2设φ是单位圆盘D上的解析自映射,算子是紧算子的充要条件是算子D2Cφ有界,且同时满足
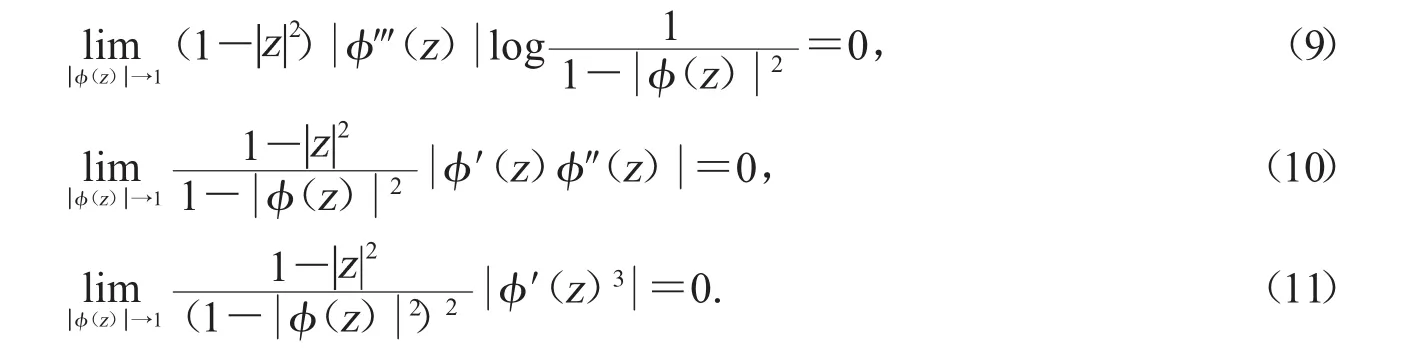
证明:充分性
若算子 D2Cφ有界,且(9)、(10)、(11)成立,由假设可知,对于∀ε>0,则∃δ∈(0,1),当时满足
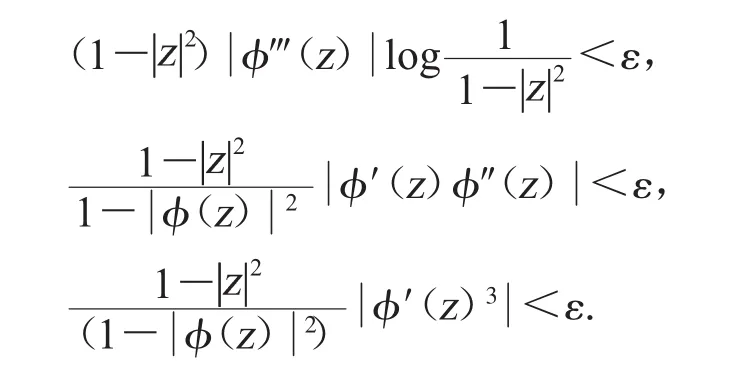
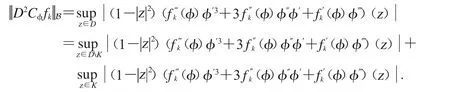
分别对A、B项进行估计,
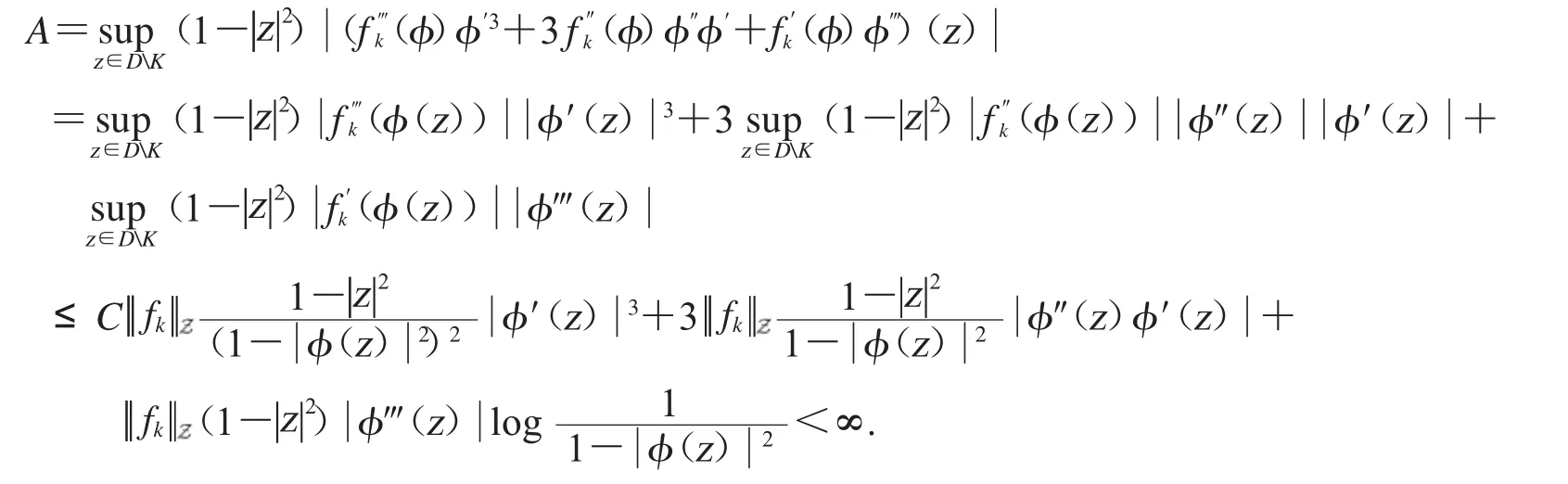
应用(4)、(5)和(6)对 B 进行估计
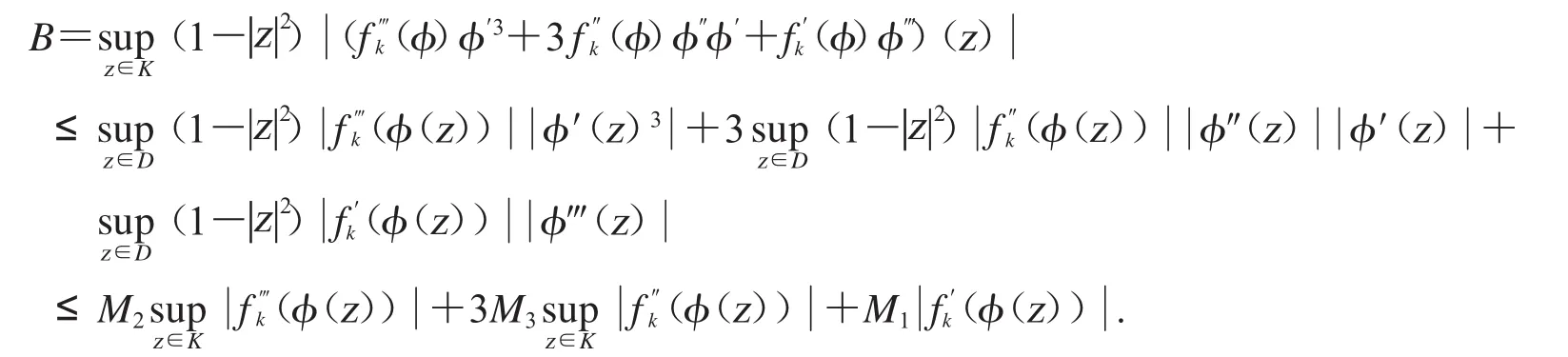
由于当k→∞时,fk在D上的紧子集一致收敛到0,由柯西估值定理,k→∞时,在D上的紧子集K上有.因此,若k→∞时,ε任意小,我们得到
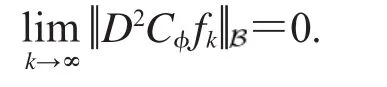
根据引理3.1.1,充分性得证.
必要性
若 D2Cφ是空间上的紧算子,显然D2Cφ是有界算子,选取D上的点列{zk}k∈N使得当k→∞时,有,也就是,对任意的ε>0,存在正整数N,使得当时k>N,有.
选取函数族
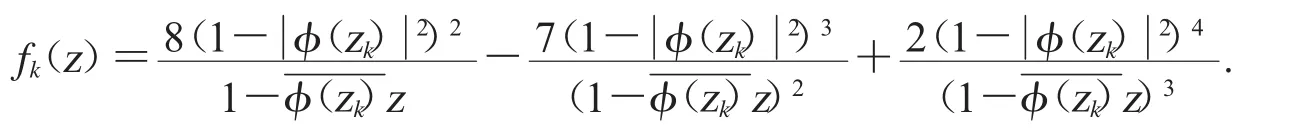
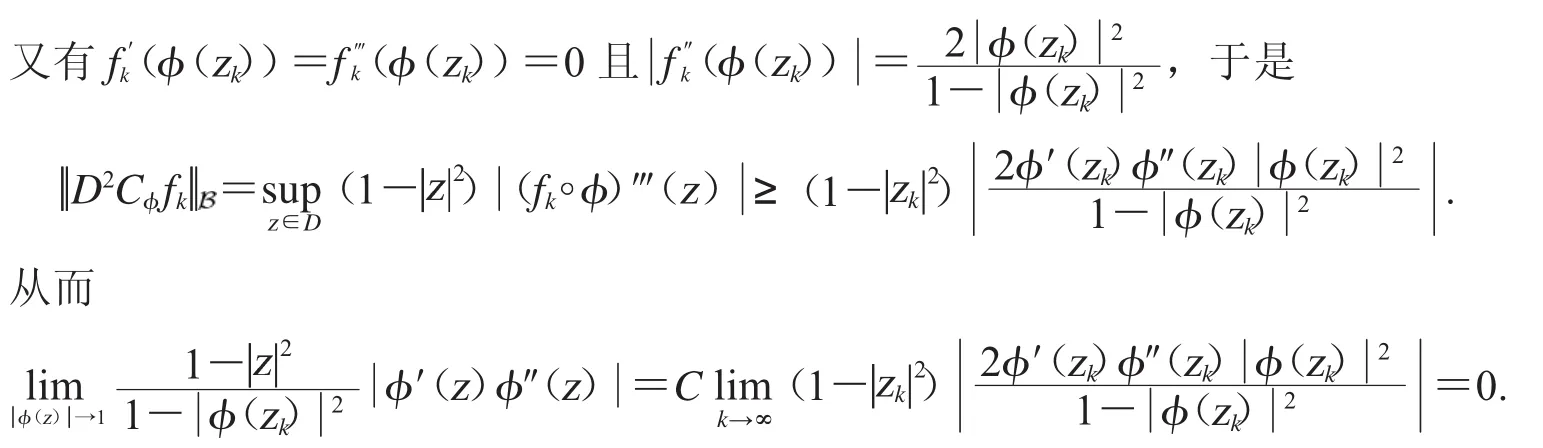
即(3.10)成立.
选取函数
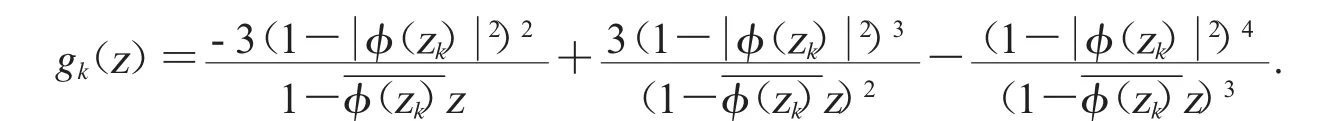
{gk}也是空间上内闭一致收敛于0的有界列,故由引理2.3得
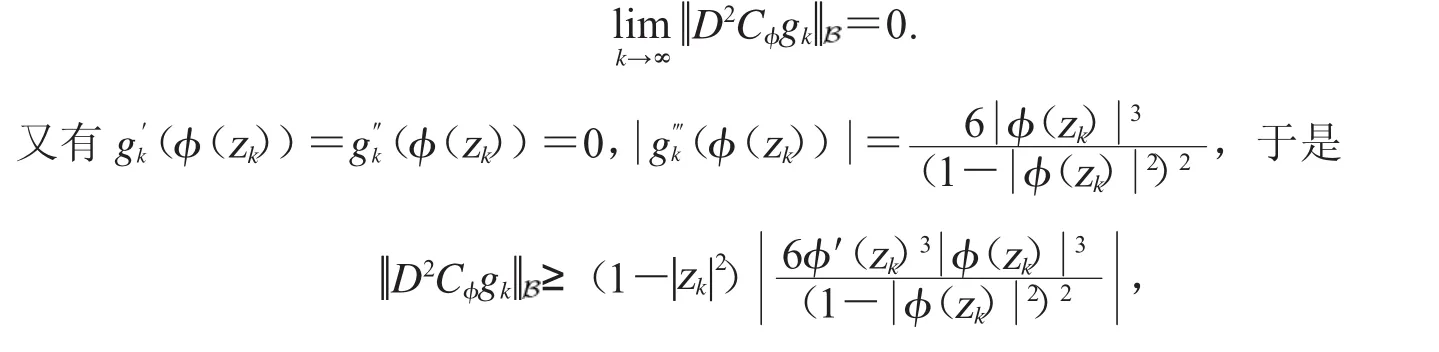
所以
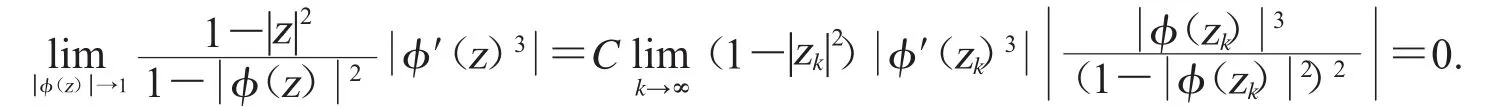
即(3.11)成立.
选取函数
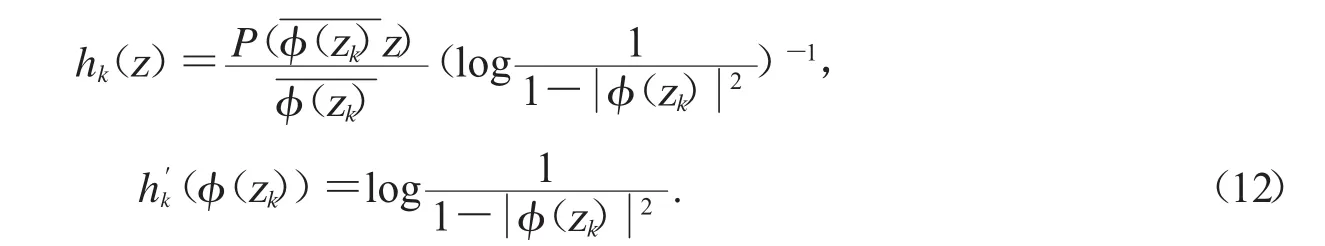
{hk}也是空间上内闭一致收敛于0的有界列,由引理2.3得
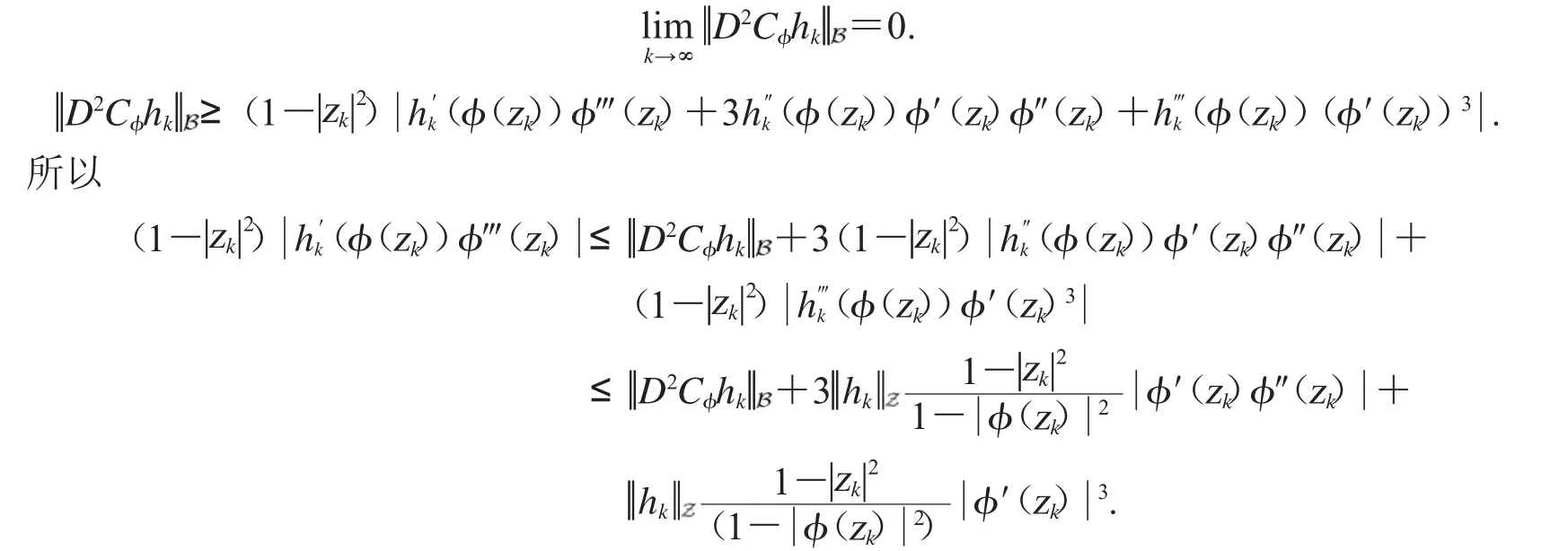
由(10)、(11)、(12)式得
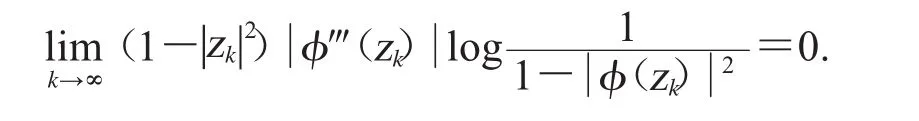
即(9)成立.
[1]NORDGREN E A.Composition operators[J].Canad J Math,1968,20:442-449.
[2]COWENJRCC,MACCLUER B I.Composition operators on spaces of analytic functions[M].Boca Raton:CRC press,1995.
[3]SHAPIRO J H.Composition operators and classical function theory[M].New York:SpringerVerlag,1993.
[4]ZHU K.Bloch type spaces of analytic functions[J].Rocky Mountain J Math,1993,23(3):1143-1177.
[7]LONG J,QIU C,WU P.Weighted composition followed and proceeded by differentiation operators from Zygmund spaces to Bloch-type spaces[J].Journal of Inequalities and Applications,2014,2014(1):152-163.
[8]SHI Y,LI S.Differences of composition operators on Bloch type spaces[J].Complex Analysis and Operator Theory,2017,11(1):227-242.
[9]ZHOUZ,CHER.Onthecompositionoperatorson the Bloch space of several complex variables[J].Science in China Series A:Mathematics,2005,48:392-399.
[10]CLIFFORDJ H,ZHENG D.Composition operators on Bergman spaces[J].Chinese Annals of Mathematics,2003,24(4):433-448.
[11]COUPETB.Decomposition atomique des espaces de Bergman[J].IndianaUniversityMathematicsJournal,1989,38(4):917-941.
[12]HU Q,ZHU X.Compactgeneralized weighted composition operatorson the Bergman space[J].Opuscula Mathematica,2017,37(2):303-312.
[13]YE S,HU Q.Weighted composition operatorson the Zygmund space[J].Abstract and Applied Analysis,2012,2012:1-9.DOI:10.1155/2012/462482.
[14]YES,LINC.CompositionfollowedbydifferentiationontheZygmundspace[J].Acta Mathematica Sinica,2016,59(1):11-20.
[15]TJANI M.Compact composition operators on some Mobius invariant Banach spaces[D].Michigan:Michigan State University,1996.

