对流反应扩散方程的波前解
(晋中学院 数理学院,山西 晋中 030619)
1 提出问题
近年来反应扩散方程的行波解有很多研究.文献[1~3]用不同方法得到了时滞反应扩散方程
行波解的存在性.另外非局部时滞和行波解的稳定性等也有很多结果,如文献[4,5],文献[6]在时滞反应扩散方程中加入对流项,文献[7]用上下解方法得到非局部时滞对流反应扩散方程的波前解.本文用上下解和单调迭代方法研究
(1)
的波前解.其中t>0,x∈R,D=diag(di),di>0B=diag(bi),i=1,…,n,F∈C(C([-τ,0],Rn);Rn)是连续的,记ut(x)(θ)=u(t+θ,x),θ∈[-τ,0].把u(x,t)=φ(x+ct),φ∈C2(R,Rn),ξ=x+ct,c>0代入(1)式得
Dφ″(ξ)-cφ′(ξ)+Bφ′(ξ)+Fc(φξ)=0,ξ∈R.
(2)
其中Fc(φ)=F(φc),φc(θ)=φ(cθ),波前解是单调且满足

(3)
的解.
2 证明
设
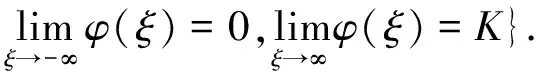
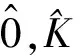
假设:
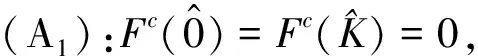
(A2):存在α=diag(αi),αi≥0,使得对所有φ,ψ∈C([-cτ,0],Rn),当0≤φ≤ψ≤K时满足

定义H:C(R,Rn)→C(R,Rn):
H(φ)(t)=Fc(φt)+αφ(t),
由引理3.1[2]知,H(φ)(t)≥0,且关于t,φ都是非减的.

(4)
下解只需改变(4)的不等号.
开始首次迭代
解
引理1[2]若A1,A2成立,则x1(t)(x11(t),…,x1n(t))Τ满足下述条件
(i)x1(t)∈Γ;
(iii)x1(t)是(2)的上解.

Dxm′′(t)+(B-c)xm′(t)-αxm(t)=-H(xm-1)(t)
解为
引理2xm(t)满足下列条件:
(B1)xm(t)∈Γ;
(B3)xm(t)是(2)的上解.

3 结论

证明 由F的连续性和Lebesque’s控制收敛定理得x(t)满足(2),

证毕.

