基于中值修正的两种Toeplitz矩阵填充的低秩逼近算法

,,

(太原师范学院 数学系,山西 晋中 030619)

1 预备知识

在科学技术高速发展的新时代下,矩阵填充在机器学习[1,2]、控制[3]、图像恢复[4]、和计算机视觉[5]等信息科学领域发挥着重要的作用.矩阵填充首先由 Cand’es 和 Recht[6]提出,主要研究的是在已知采样矩阵部分元素的前提下,合理精确地填充一个低秩矩阵,其数学表达式为:

minrank(X)

st:PΩ(X)=PΩ(D),

(1)

其中X,D∈Rn1×n2,Ω∈{1,2,…,n1}×{1,2,…,n2}

上述问题是矩阵填充最原始的问题,对于(1) 解的存在性及唯一性,Recht[6]等分别通过限制等距的性质和秩为r的矩阵D的相关性解决.近年来,在己知或者能够估计矩阵X秩的情况下,已经有许多学者提出了有效的算法,其中比较著名的是将X写为两个矩阵的乘积,即:X=UV,其中U∈Rn×r,V∈Rr×n. 基于这类简单分解模型以及交替极小化方法Tanner等提出了交替最速下降算法 (Alternating Steepest Descent,简称ASD[7]),结合 Riemannian 优化,Vandereycken 提出几何共轭梯度法 (Geometric Conjugate Gradient,简称GCG[8]).随后,Boumal 等提出 Riemannian 信赖域法 (Riemannian Trust-Region,简称RTR[9]).Mishra 等提出Riemannian几何法 (Riemannian Geometry,简称RG[10]),但是,这些算法的共同缺点是其梯度计算过程比较复杂.

另一方面,Cand’es 和Recht[6]提出大部分秩为r的低秩矩阵可以通过求解以下凸优化问题来实现矩阵的填充:

min‖X‖*

st:Xij=Mij,(i,j)∈Ω

(2)

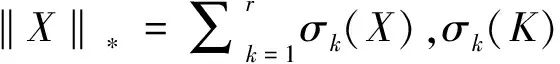
在实际应用中,采样矩阵往往具有特殊结构,如Toeplitz和Hankel结构等,因此研究特殊矩阵的填充问题很有意义.Toeplitz矩阵作为一种重要的特殊矩阵,在广泛的科学与工程领域,特别是在信号与图像处理领域发挥着重要作用.一个n×n的Toeplitz矩阵T∈Rn×n具有如下形式:

显然,Toeplitz矩阵由它的第1列和第1行共2n-1个元素决定.根据Toeplitz矩阵的特殊结构,Kailath和Sayed运用快速Fourier变换(简称FFT),提出了计算n阶Toeplitz矩阵与n维向量乘积的快速算法,其算法复杂度为O(nlogn).

在大多数的情况下,填充矩阵的秩是未知的,最近Wang等提出了基于正交匹配追踪算法(Orthogonal Matching Pursuit,简称OMP[16])的正交秩1矩阵追踪算法(Orthogonal Rank-One Matrix Pursuit,简称OR1MP[17]),但是,当填充矩阵的秩达到预设的秩时,误差精确度较低.

文章的结构如下:第二节对现有的算法进行简单的回顾,然后再详细的介绍基于中值理论的OR1MP与EOR1MP算法;第三节通过数值实验将新算法与OR1MP、EOR1MP算法进行比较,验证算法的有效性;第四节对全文进行总结.

2 算法

2.1 算法回顾

2.1.1 正交秩1矩阵追踪算法(简称OR1MP)

第一步:设采样矩阵YΩ=PΩ(D),maxiter,tol=10-3,初始矩阵X0=0,k:=1;

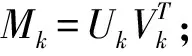
第六步:如果k≥maxiter或者‖Rk‖F/‖YΩ‖F≤tol,停止计算;否则,令k:=k+1,跳转到第二步.

2.1.2 经济正交秩1矩阵追踪算法(简称EOR1MP)

第一步:设采样矩阵YΩ=PΩ(D),maxiter,tol=10-3,初始矩阵X0=0,k:=1;

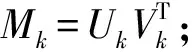
第三步:计算Xk-1和Mk的最优权向量αk,min‖α1Xk-1+α2(Mk)Ω-YΩ‖2;

第六步:如果k≥maxiter或者‖Rk‖F/‖YΩ‖F≤tol,停止计算;否则,令k:=k+1,跳转到第二步.

2.2 基于中值修正的两种新算法

2.2.1 中值修正的正交秩1矩阵追踪算方法(简称MOR1MP)

第一步:设采样矩阵YΩ=PΩ(D),maxiter,tol=10-3,初始矩阵X0=0,k:=1;

第六步:如果k≥maxiter或者‖Rk‖F/‖YΩ‖F≤tol,停止计算;否则,令k:=k+1,跳转到第二步.

2.2.2 中值修正的经济正交秩1矩阵追踪算法(简称MEOR1MP)

第一步:设采样矩阵YΩ=PΩ(D),maxiter,tol=10-3,初始矩阵X0=0,k:=1;

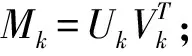
第六步:如果k≥maxiter或者‖Rk‖F/‖YΩ‖F≤tol,停止计算;否则,令k:=k+1,跳转到第二步.

3 数值实验

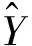
表1 当p=0.4且maxiter=20时,算法OR1MP和MOR1MP的比较

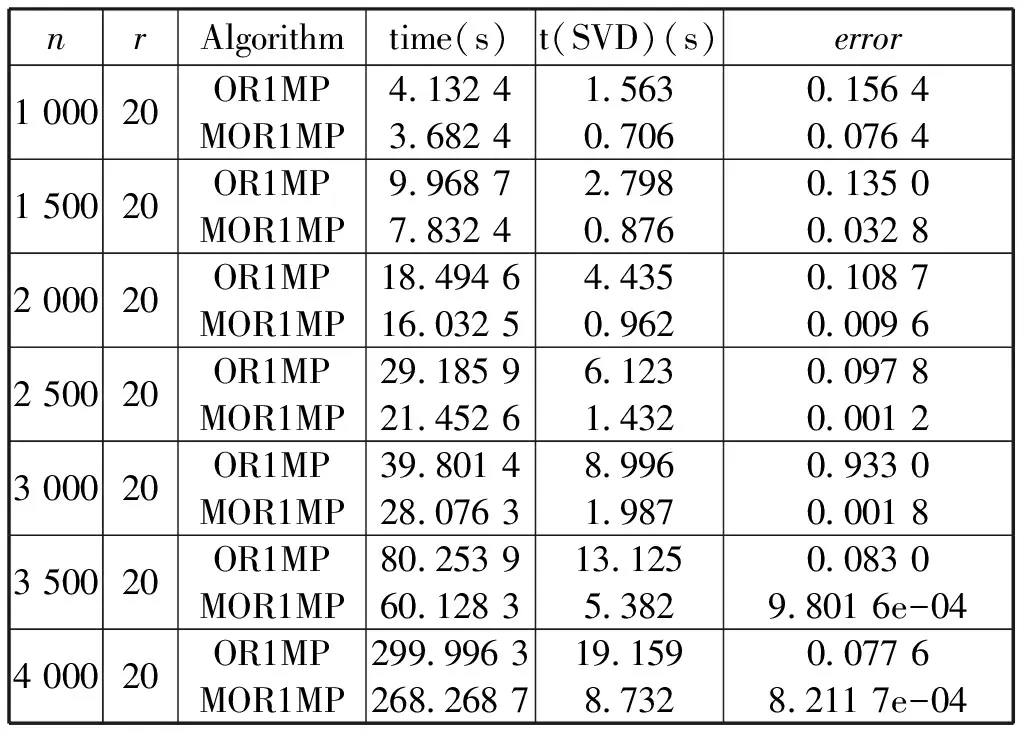
表2 当p=0.5且maxiter=20时,算法OR1MP和MOR1MP的比较

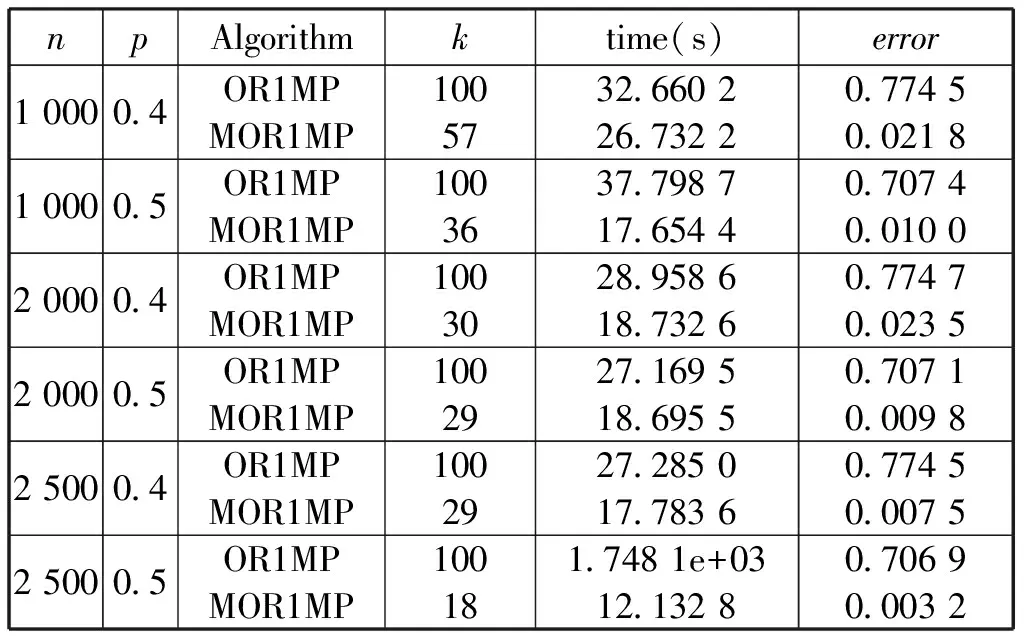
表3 当‖Rk‖F/‖YΩ‖F≤tol时,算法OR1MP和MOR1MP的比较

注. 在表 3.3 中,设置最大迭代次数为 100.

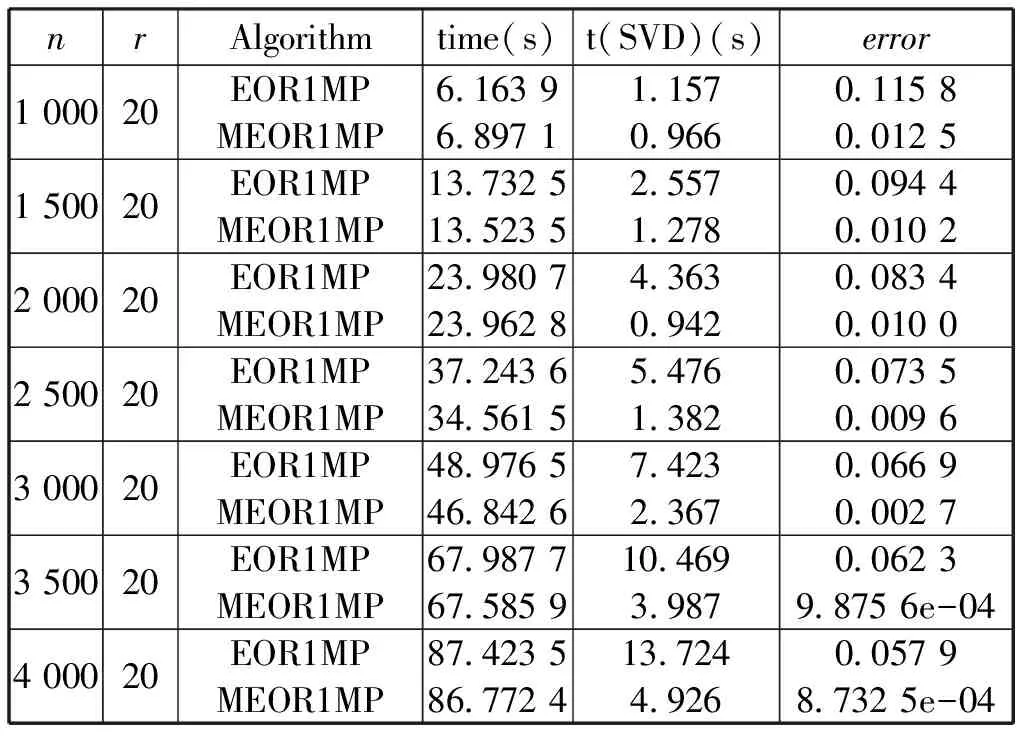
表4 当p=0.4且maxiter=20时,算法EOR1MP和MEOR1MP的比较

表5 当p=0.5且maxiter=20 时,算法 EOR1MP和MEOR1MP的比较

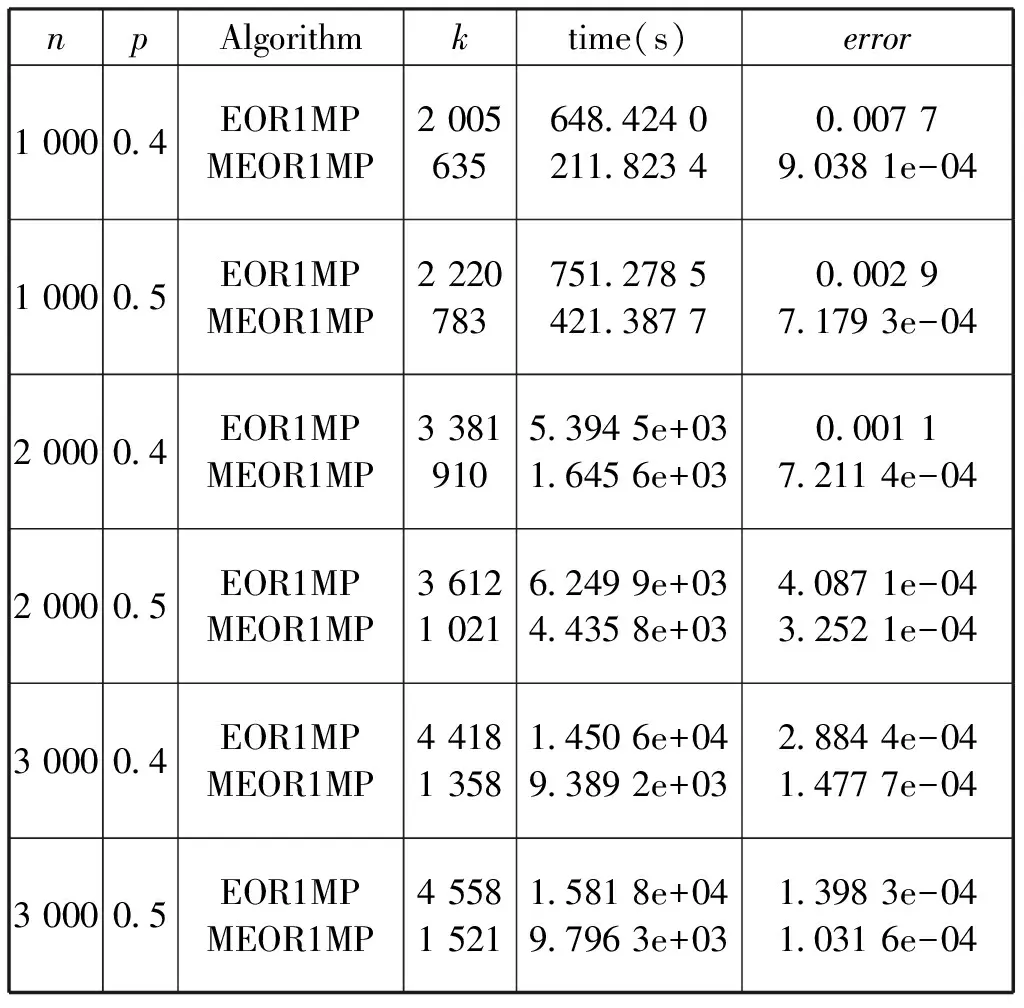
表6 当‖Rk‖F≤tol时,算法 EOR1MP和 MEOR1MP 的比较.

4 总结

本文中,基于中值理论,提出了两种修正的Toeplitz矩阵填充的新算法,在进行实验的过程中,使得被填充矩阵始终保持Toeplitz矩阵的结构,保证了矩阵的快速奇异值分解,这在很大程度上缩短了矩阵填充的奇异值分解的时间,从而降低了算法的整体时间,通过数值实验,说明新算法无论在精确度方面,还是时间上,都有更好的优势.