相容关系模型及其在逻辑优化中的应用*

王好为，闫继雄，柴 晶，陈泽华

太原理工大学 信息工程学院，太原 030024

1 引言

逻辑表达式化简技术[1]是数字电路中的一个重要内容，其作用是能在保证原电路功能不变的情况下，减少输入电路中门电路的个数，使得电路更简洁、更安全。

传统的逻辑表达式化简方法有公式法[2]、卡诺图法[2]、Q-M算法[3]和立方体法[4]等。其中公式法不仅需要熟练使用逻辑代数的相关知识，而且不易编程；卡诺图法是一种直观的逻辑表达式化简方法，但是当输入变量个数超过6时，难以表达；Q-M算法是基于卡诺图法的一种改进算法，但是算法复杂度依旧很高；立方体法具有较低的时间复杂度，但是对于多变量表达式，其计算过程不易理解。

近年来，有很多学者在逻辑表达式化简方面进行了研究，并取得了较大的进展。他们对传统方法进行了改进，包含对卡诺图法的改进算法[5-6]和对Q-M算法的改进算法[7-8]。Gómez等人[9]依据逻辑表达式的拓扑和统计特性提取了其中的质蕴涵项，将表达式的化简过程转化为最小项的化简过程，从而降低了计算的复杂性；Chowdhury等人[10]基于MZI（Mach-Zehnder interferometer）的模式匹配方案将逻辑表达式转化为逻辑电路，根据去除电路的辅助线达到约简的目的，但该方法依赖于硬件电路的实验结果，并且实验成本较高，不具有实用性；陈泽华等人[11]基于粗糙集的等价关系模型实现了普通真值表的快速并行约简，但是该方法处理逻辑表达式时需要将其展开为最小项，并转化为完整输入状态的真值表，转化过程较为繁琐，也会增加额外的空间复杂度。

粒计算是一种处理具有不确定性的大量复杂信息的方法论，它通过把复杂问题抽象、划分，从而转化为若干较为简单的问题，有助于更好地分析和解决问题。根据数字电路相关知识，逻辑表达式的与或式均可以转化为特殊的不完备决策表。近年来，众多学者基于粒计算对不完备决策表的研究取得了较大的进展。邵明文等人[12]基于粗糙集理论重新定义了上下近似的概念，然后计算不完备决策表的分辨矩阵，提取决策表中的有效规则；杨习贝[13]和吴伟志[14]等人针对多尺度信息系统提出了各自的规则提取算法，为粗糙集带来新的生机[13]；官礼和等人[15]基于粒计算的属性重要度理论，对决策表的属性进行排序，依次加入属性值，从而提取得到规则，该算法在由粗到细的粒度空间下进行分析，降低了算法的时间复杂度，但是得到的规则集不能保证为最简。

本文基于相容关系，针对数字电路中任意的逻辑表达式，提出了一种快速的逻辑表达式化简算法。该算法首先将任意的逻辑表达式转化为与或式，并表示为本文定义的不完备真值表；然后在多粒度空间下，分别计算相容逻辑信息系统中每个属性集合的相容矩阵和逻辑关系矩阵，根据逻辑关系矩阵的性质判断该属性集是否可以得到新的规则；最后将提取的规则转化成表达式，该表达式即为最简逻辑表达式。本文通过设定算法终止条件从而加快算法收敛，并通过定理证明和实例分析验证了本文算法的正确性。

2 预备知识

2.1 逻辑表达式化简相关概念

数字电路是用数字信号完成对数字量进行逻辑运算的电路，其处理的信号均为数字量的信号，且均可以用0和1组成的二进制数来表示信号的大小。下面介绍本文用到的一些数字电路的基本知识。

定义1[1]（逻辑表达式、与或表达式、最小项、最简与或表达式）逻辑表达式是用逻辑运算符将关系表达式或逻辑量连接起来的有意义的式子；与或表达式是将逻辑表达式转化为若干个只含与、非运算的单项式，并用或运算进行连接的式子；最小项是所有输入变量的乘积，每个变量都以它的原变量或反变量的形式在乘积中出现且仅出现一次；与或表达式中的任意一个单项式均可以转化为若干个最小项的和；逻辑表达式化简就是要消去与或表达式中冗余的乘积项及每个乘积项中冗余的变量，以得到逻辑表达式的最简与或表达式。

逻辑表达式化简遵循如下逻辑代数基本定律。

（1）0-1律

（2）结合律、交换律、分配律

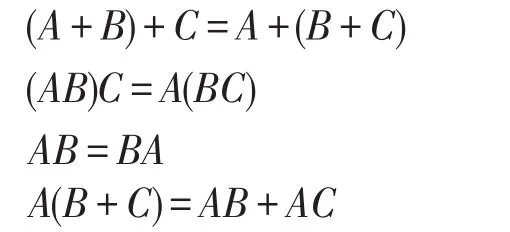
（3）反演律（摩根定理）

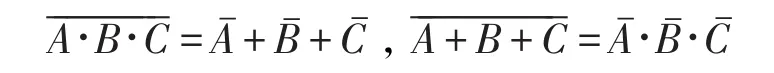
本文通过例1说明上述几种表达式的表现形式，并根据计算实现表达式之间的转换。

例1一个数字电路的逻辑表达式为：

将其转化为与或表达式为：

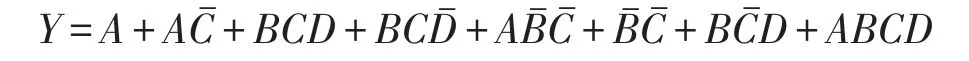
对于四输入的逻辑电路，单项式A可转化为8个最小项之和：

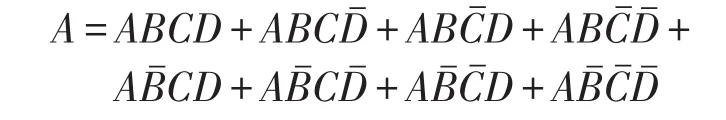
将与或表达式转化为最简与或表达式为（卡诺图法[2]）：

2.2 不完备决策表与不完备真值表

决策表是粗糙集中重要研究内容，其定义如下。

定义2[12]（决策表）决策表可以用一个四元组DT=(U,A,V,f)来表示。其中U表示对象的非空有限集合，称为论域；A=C⋃D表示属性集合且C⋂D=∅，C表示条件属性集，D表示决策属性集；V=表示属性a的值域；f:U×A→V表示决策表中的一种映射关系，它为每个对象在每个属性上赋予了一个信息值，即∀a∈A,x∈U,f(x,a)∈Va。若存在a∈A,x∈U使得f(x,a)未知（记作f(x,a)=*），则称决策表是不完备的，否则称决策表是完备的。

相容关系是处理不完备决策表的重要理论工具，Kryszkiewicz最初对其进行了数学定义。

定义3[12]（不完备决策表）设DT=(U,A,V,f)为一个不完备决策表，对于任意的属性集合P⊆A，定义U上的一种相容关系SIM(P)为：

对于任意的对象x∈U，定义集合SP(x)={y|(x,y)∈SIM(P)}，表示论域中x的相容类的集合；基于此相容类集合再定义集合U/SIM(P)={SP(x)|x∈U}={X1,X2,…,Xk}表示U关于P的覆盖，即满足且存在Xi,Xj∈U/SIM(P)使得Xi⋂Xj≠ ∅ 。

真值表是用来表征逻辑事件输入和输出之间全部可能状态的表格，表示了电路中的逻辑因果关系。把组合电路中各输入变量的所有可能取值与相应的输出值，以表格形式一一列举出来，这种表格就称为真值表。

由2.1节的相关知识，若将与或表达式中的每一项看作一条逻辑规则，则逻辑表达式可表示为不完备决策表，其中每一项缺失的属性可看作不完备决策表中缺失项“*”。与一般不完备决策表不同的是，由与或表达式转化的决策表中其决策值均为“1”，且条件属性中的缺失项“*”可且只可取值为“0”或“1”，因此是一种特殊形式的不完备决策表。本文将这种决策表定义为不完备真值表。

定义4（不完备真值表）真值表可以用一个四元组T=(U,R,V,f)来表示。其中U为论域，表示电路所有可能的状态；R=X⋃Y表示所有输入输出逻辑变量，X={X1,X2,…,Xm}表示所有输入逻辑变量，m为输入变量的个数，Y={Y1,Y2,…,Yn}表示所有输出逻辑变量，n为输出变量的个数；V表示电路的所有逻辑变量值；f:U×R→V是一个信息函数，它指定U中每一个对象、R中每一个逻辑变量所对应的逻辑值。若存在a∈R,x∈U使得f(x,a)未知（记作f(x,a)=*），则称该真值表为不完备真值表。

一般情况下，若真值表中不含有无关项，即V∈{0,1}，每一行的所有输入值便可以组成一个最小项。但是由与或表达式转化的不完备真值表中，输入值中含有无关项，即V∈{0,1,∗}（“*”表示无关项），此时真值表中每一行变量值乘积后便不是最小项，而是一般的与或式。

例2沿用例1，将与或表达式转化为真值表，如表1所示。

Table 1 Incomplete truth table for corresponding logical function表1 逻辑函数对应的不完备真值表

不完备真值表为T={U,X⋃Y,V,f}，其中U={1,2,3,4,5,6,7,8},X={A,B,C,D},Y={Y}。

3 逻辑关系矩阵

以下主要介绍逻辑关系矩阵的计算方法，并给出相应定理说明逻辑关系矩阵的意义。

定义5（相容矩阵）在不完备真值表T={U,X⋃Y,V,f}中，U={u1,u2,…,ul}(l=|U|)，对于任意的属性集则定义P的相容矩阵为：

其中，aij的计算公式如下：

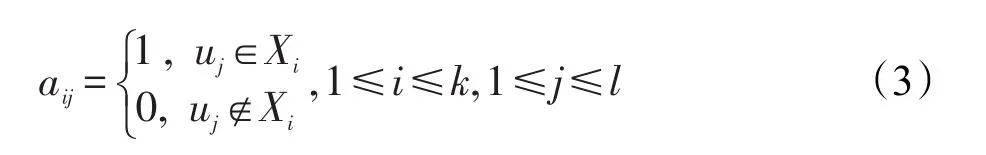
设(X-P)为属性空间X下除去P的剩余属性集合，同样可求得(X-P)的相容矩阵XX-P。

定义6（逻辑关系矩阵）在不完备真值表T={U,X⋃Y,V,f}中，对于P⊆X，定义P的逻辑关系矩阵为：

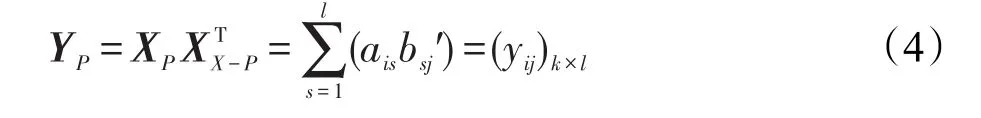
逻辑关系矩阵是本文提出的用于判别是否可以提取约简规则的判断依据，满足如下定理。

定理1若YP的第i行（1≤i≤k）的值均不为“0”，则相容类Xi必然可以得到一条确定性最简规则。

证明由式（4）得YP=XPXTX-P，则YP的第i行、第j列元素的计算公式为：

若cij≠0 ，说明Xi中的“1”与Xj中的“1”对应相乘，即属性P的第i种取值与剩余属性的第j种取值可以合成最小项；若对所有的1≤j≤q均有cij≠0，则属性x的第i种取值可以与剩余属性的任意取值合成最小项，即覆盖剩余属性的所有取值情况。根据逻辑函数基本定律，属性P的第i种取值必是一条输出规则；由于粒度是从粗变细，在较粗粒度下没有辨识的规则，在细粒度下一定会辨识出最简规则，即输出的规则为最简规则。

4 基于相容关系的逻辑表达式化简算法

4.1 启发式算子

为了使本文算法更加快速地收敛，需计算出不完备真值表中所含的所有规则数，而在算法计算过程中已经被寻到的规则数可以作为启发式算子加快算法的效率。

定义7（总规则数）在不完备真值表T={U,X⋃Y,V,f}中，记表中的总规则数为N，由于有无关项的存在(∗∈{0,1})，且每一行的i个无关项有2i种组合，N的计算公式为：其中，g(j)表示真值表中第j行无关项“*”的个数。

在算法计算过程中，已寻到的规则数n是不断更新的，并且已寻到的规则不能重复被计算为规则数，因此有如下定义。

定义8（最小项集合）已寻到的规则的输入项均可以转化为最小项，这些最小项放置在同一集合即为最小项集合。

定义寻到的最小项的集合为NR，用来判断新找出的规则中是否已包含已寻到的规则。

本文为了避免对规则冗余性的判断，利用逻辑关系矩阵提出如下定理。

定理2在T={U,X⋃Y,V,f}中，已知逻辑关系矩阵YP(P⊆X)的第Row行全不为0元素，且第Col列与第Row行所组合的规则并未被寻到（Row与Col均为集合），即该规则的输入项转化成的最小项不存在于NR中，则属性集合P寻到的规则数为：

其中，yij表示YP中第i行、第j列的元素。

证明假设在属性集合P下按二进制顺序排列得到的逻辑关系矩阵YP存在全不为“0”的行，找出该行位置记为Row，则其行数为U关于P的相容类类别数，YP中元素的列数则代表U关于(X-P)的相容类类别数，而等价类是由属性值得到的，便可得到对应属性的取值，据此便可得到找寻到的规则NR。令新规则与集合R相减即NR-R（即存在于NR且不存在于R的规则），得到还未被找到的规则，该规则下在YP中对应的列记为Col。

推论已寻到的规则数n等于所有属性集合寻到的规则数的总和，即

规则数n和原规则数N存在如下定理，可加速算法的收敛。

定理3当已寻到的规则数n和真值表的总规则数N满足条件n=N时，算法即收敛。

4.2 算法描述

本文基于多粒度的思想，提出了基于相容关系的逻辑表达式化简算法，该算法的计算步骤如下：

算法1基于相容关系的逻辑表达式化简算法

输入：任意逻辑表达式Y=f(A,B,C,D,…)。

输出：最简逻辑表达式。

1.将一般逻辑表达式转化为析取范式，并转化为真值表；

2.计算N，初始化ω=1，n=0，R=∅，rl=∅；

3.计算输入属性子集P在粒度ω下(即满足||P=ω)的逻辑关系矩阵YP；

4.找出YP中全不为0的行，并找出对应规则，计算nx，判断nx是否大于0；

5.若nx＞0，则依次记录{NR-R}至R，所得规则记录至rl，并更新n值；

6.若nx=0，则转至步骤7；

7.判断是否满足n=N，若不满足转至8，否则转至9；

8.判断ω是否达到最大值（ω最大为|X|），若没有达到，则ω=ω+1，返回步骤3继续计算，否则转至步骤9；

9.将rl中的规则转化为逻辑表达式，输出逻辑规则。

4.3 复杂度分析

对于真值表T={U,X⋃Y,V,f}，由算法步骤可知，步骤1、2的复杂度均为O(1)，步骤3中，在第ω次迭代情况下，计算所有属性子集的相容矩阵复杂度为，而计算所有剩余属性集的相容矩阵的复杂度，因此计算逻辑关系矩阵的复杂度为O(2×步骤4～7为规则提取过程，其复杂度为O(1)。由算法步骤可知，步骤3～8为迭代过程，每次迭代的算法复杂度为，其迭代次数在最坏的情况下为|X|次，因此总复杂度为实际上，对于在第ω次迭代情况下求得的所有逻辑关系矩阵，实际为在第|X|-ω次迭代情况下求得的所有逻辑关系矩阵的转置，不用重复求取，因此算法1在最坏的情况下，其实际复杂度为O(2|X|+1/2)=O(2|X|)。

5 实验与分析

5.1 实例说明

例3沿用例2，不完备真值表为T={U,X⋃Y,V,f}，其中U={1,2,3,4,5,6,7,8},X={A,B,C,D},Y={Y}。

置R,rl={∅}，根据式（5）可知，22+…+20=25，置n=0，ω=1。

在ω=1的粒度下，每种属性集合即为{{A},{B},{C},{D}}，其属性空间内剩余属性的集合为{{B,C,D},{A,C,D},{A,B,D},{A,B,C}}，根据定义3可以计算得到：

根据式（3）、式（4），分别计算每个属性集合P的相容矩阵，可得：

同理，属性集合(X-P)的相容矩阵也皆可求得：

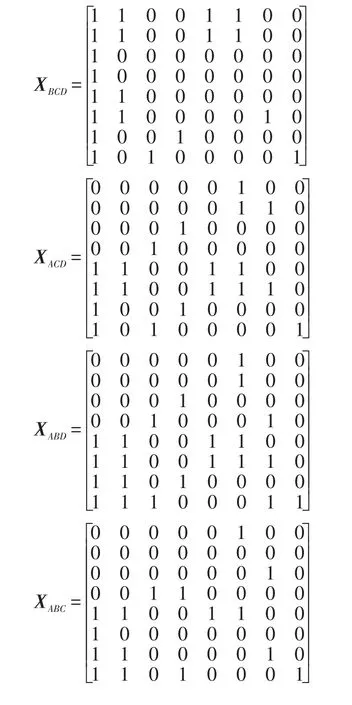
再根据式（4），计算各属性集合的逻辑关系矩阵，得：

接下来需要判断逻辑关系矩阵中是否存在全不为“0”的行。由以上计算结果可知YA的第二行全不为“0”，从而得知U/SIM(A)的第二个相容类可以得到新规则，即NR={m8,m9,m10,m11,m12,m13,m14,m15}。新规则在YA的位置为：

根据式（8）可计算得到：

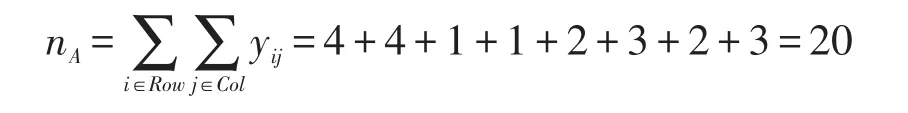
由nA＞0，则将{NR-R}存入R，即R=NR，把最简规则rl1={A=1→Y=1}存入rl。因为n=n+nA=所以需要在粒度更细的空间下继续计算。

在ω=ω+1=2的情况下，每种属性集合为{{A,B},{A,C},{A,D},{B,C},{B,D},{C,D}}，其属性空间内剩余属性的集合为{{C,D},{B,D},{B,C},{A,D},{A,C},{A,B}},同样可计算得出：

由于已经区分出属性A下取值为“1”的规则，无需判断YAB、YAC、YAD的第3、4行（相容类中A取值为1），该逻辑关系矩阵不能提取新规则。

根据YBC的值，可以判断出属性{BC}在取值为“00”和“11”的情况下可以获得新规则，即NR={m0,m1,m8,m9,m6,m7,m14,m15},NR-R={m0,m1,m6,m7}。因此新规则的位置为Row={1,4},Col={1,2}，可得nBC=1+1+1+1=4＞0，将 {NR-R}存入R可得R={m0,m1,m6,m7,m8～m15}，把最简规则rl2={B=0∧C=0→Y=1},rl3={B=1∧C=1→Y=1}存入rl。由于n=n+nBC=24＜N，需要继续计算。

根据YBD的值，可以判断属性{BD}在取值“11”的情况下可以获得新规则，即NR={m5,m7,m13,m15}，而NR-R={m5}，因此新规则的位置为Row={4},Col={1}，可得nBD=1＞0。将 {NR-R}存入R得R={m0～m1,m5,m6～m15}，最简规则rl4={B=1∧D=1→Y=1}存入rl。由于n=n+nBD=25=N，计算结束。

最终得到该算例的4条最简规则（在集合rl中），将规则表示为逻辑表达式，即算法输出为Y=A+BC+BˉCˉ+BD，与卡诺图法结果一致（见例1）。

5.2 算法正确性分析

卡诺图法是公认的简单、正确的逻辑表达式化简算法，算法1与卡诺图法等价，证明如下。

卡诺图法：设一个普通的真值表具有m个逻辑输入，K为真值表所对应的卡诺图[1,3]。K中任意一个依照规则得到的圈Ωi由2k个取值为1的最小项组成(0≤k≤m)，Ω={Ωi|Ωi∈K}。Θi={com(Ωi)}表示Ωi中的公共因子。根据卡诺图化简原则，Θi是Ωi的约简，构成卡诺图的化简结果。令中最小项个数，中公共因子的变量个数，即约简后输入变量的个数。存在如下关系

在算法1中，设在第ω次迭代情况下，根据输入属性集合P求得的某个逻辑关系矩阵为YP，且其维度为2|P|×2|X-P|。根据逻辑关系矩阵的定义，可知其每一个元素均表示P的相容类与(X-P)的相容类的相交项，即为最小项的矩阵表示。若YP中存在某行元素全为非0元素，根据定理2，可知P的某个相容类可以覆盖(X-P)的所有相容类，即在该相容类下存在2|X-P|个取值为1的最小项。设P在该相容类下的取值为因此，根据YP可以得到卡诺图的一个圈Ωi。由此可知，算法1与卡诺图原理一致，即满足等价性。

在例3中，YA的第二行全为非0元素，则在A=1的相容类下，存在2|X-P|=8个最小项，分别为ABCD、此时根据YA可得到卡诺图一个圈Ω1，如图1所示。

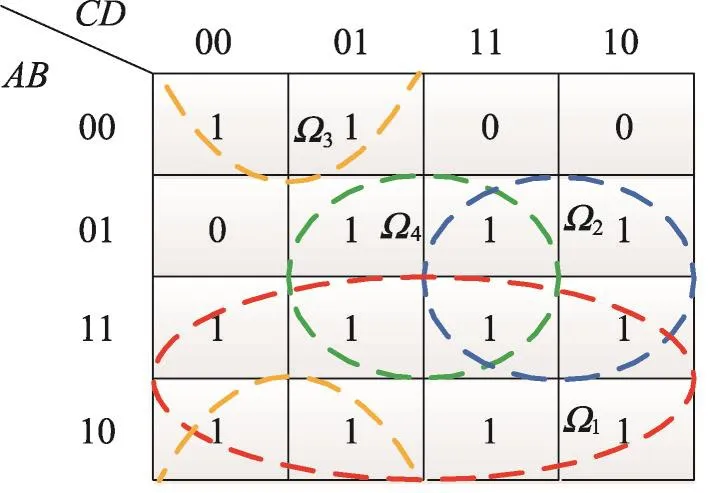
Fig.1 Sketch map for Karnaugh map reduction图1 卡诺图化简示意图

同理，在第二次迭代运算时，可得到卡诺图中另外的3个圈Ω2、Ω3、Ω4，如图1。由于已覆盖卡诺图中的全部“1”元素（对应于算法1中判断n是否等于N），算法输出为

等价性证明则保证了算法1的正确性。

6 结束语

本文针对数字电路中逻辑表达式化简问题，提出了基于相容关系的逻辑表达式化简算法。算法首先将一般逻辑表达式转化为与或表达式，输入项中含有无关项的真值表，然后在不同粒度空间下分析真值表中隐含的最简逻辑规则，最后将所有逻辑规则再转化为逻辑表达式，实现逻辑表达式的快速化简。本文算法有以下特点：（1）相比于传统算法，本文从多粒度的角度出发，使规则提取变得直观，并且保证了提取规则的完整性；（2）在粒度为ω的粒度空间下，能同时计算属性子集个数为ω和个数为的相容矩阵，避免了在粒度为的粒度空间下重新计算各属性子集的相容矩阵，降低了算法复杂度；（3）通过定义已寻到的规则数n来判断是否可以跳出循环输出结果，加速了算法的收敛，提高了效率；（4）通过算法正确性分析可知本文算法与卡诺图法等价，且本文算法没有输入变量个数的限制，更具有一般性。本文算法的不足之处在于，虽然在一定程度上降低了算法的运算复杂性，但是在最坏情况下仍没有突破指数阶的算法复杂度。因此，如何解决复杂度为指数阶的NP问题仍是亟待思考的问题，相关工作仍在继续。

[1]Yu Mengchang.Concise course of digital electronic technology[M].Beijing:Higher Education Press,2006.

[2]Kang Huaguang.Fundamentals of electronic technology—digital part[M].Beijing:Higher Education Press,2006.

[3]Quine W V.The problem of simplifying truth functions[J].American Mathematical Monthly,1952,59(8):521-531.

[4]Bian Jinian,Xue Hongxi,Su Ming,et al.Digital system design automation[M].Beijing:Tsinghua University Press,2005.

[5]Khalid A T M S,Ahmed F,Karim M A.A composite mapping technique for simplification of multi-variable Boolean expressions[C]//Proceedings of the IEEE 1995 NationalAerospace and Electronics Conference,Dayton,May 22-26,1995.Piscataway:IEEE,1995:256-262.

[6]Solairaju A,Periyasamy R.Optimal Boolean function simplification through K-map using object-oriented algorithm[J].International Journal of Computer Applications,2011,15(7):28-32.

[7]Tomaszewski S P,Celik I U,Antoniou G E.WWW-based Boolean function minimization[J].International Journal of Applied Mathematics&Computer Science,2003,13(4):577-583.

[8]Huang Jiangbo.Programing implementation of the Quine-McCluskey method for minimization of Boolean expression[J/OL].arXiv:1410.1059.

[9]Gómez L,Gómez R,Garcia B.Some simplifications of Boolean expressions using their topological and statistical properties[J].International Journal of Electronics,1981,51(2):145-155.

[10]Chowdhury R R,Bandyopadhyay C,Dutta P,et al.A Boolean expression based template matching technique for optical circuit generation[C]//Proceedings of the 2016 International Conference on Advances in Information Communication Technology&Computing,Bikaner,Aug 12-13,2016.New York:ACM,2016:36.

[11]Chen Zehua,Ma He.Granular matrix based rapid parallel reduction algorithm for MIMO truth table[J].Journal of Electronics and Information Technology,2015,37(5):1260-1265.

[12]Shao Mingwen,Zhang Wenxiu.Dominance relation and rules in an incomplete ordered information system[J].International Journal of Intelligent Systems,2005,20(1):13-27.

[13]Yang Xibei,Qi Yong,Yu Dongjun,et al.Rough set approach to incomplete multiscale information system[J].Scientific World Journal,2014,1:538968.

[14]Wu Weizhi,Qian Yuhua,Li Tongjun,et al.On rule acquisition in incomplete multi-scale decision tables[J].Information Sciences,2017,378(C):282-302.

[15]Guan Lihe,Hu Feng,Han Fengqing.A rule induction algorithm in incomplete decision table based on attribute order[J].Journal of Intelligent&Fuzzy Systems,2016,30(2):961-969.

附中文参考文献：

[1]余孟尝.数字电子技术基础简明教程[M].北京:高等教育出版社,2006.

[2]康华光.电子技术基础数字部分[M].北京:高等教育出版社,2006.

[4]边计年,薛红熙,苏明,等.数字系统设计自动化[M].北京:清华大学出版社,2005.

[11]陈泽华,马贺.基于粒矩阵的多输入多输出真值表快速并行约简算法[J].电子与信息学报,2015,37(5):1260-1265.