优化加权核K-means聚类初始中心点的SLIC算法*

杨 艳，许道云

贵州大学 计算机科学与技术学院，贵阳 550025

1 引言

所谓超像素（superpixel）是指图中局部的、具有一致性的、能够保持一定图像局部结构特征的子区域，这些小区域大多保留了进一步进行图像分割的有效信息。近年来，超像素作为一种图像预处理技术，被广泛应用于计算机视觉领域，逐渐成为研究热点之一。2003年，Ren等人[1]首次提出了超像素的概念并应用于图像分割中，经过不断的发展，超像素在图像分割领域的应用日益成熟。除此之外，超像素分割算法还被应用于图像处理的各个方面，如前景提取算法、目标识别算法等。至今，针对超像素分割算法的研究取得了丰硕的成果[2-5]，在各种各样的应用场景[6-8]中，不同的超像素分割算法被提出。目前，已有的超像素分割算法可分为两类：基于图论的算法和基于梯度下降的算法。基于图论的算法是将分割问题转化为能量函数最小化问题，将图像中的像素点看作图节点，并赋予节点与节点间的边适当的权值，然后采用各种分割标准对图进行划分来形成超像素。基于梯度下降的算法是从最初的像素聚类开始，采用梯度法迭代修正聚类结果直至满足收敛条件，从而形成超像素。表1提供了这两类方法中相关算法的性能对比结果。

所有超像素分割算法在Berkeley SegmentationDatabase公共数据集上进行实验，通过边缘贴合度，包括“欠分割错误率（under-segmentation error）”和“边缘召回率（boundary recall）”，来评估算法的性能。在表1中，基于图论的经典算法有Shi等人提出的NC05算法以及Moore等人[9]提出的SL08算法。NC05算法利用轮廓特征和纹理特征递归地进行图像分割，该算法生成规则的超像素，但边缘贴合度较差，计算速度较慢。SL08算法采用寻找最优路径的方式不断地在垂直和水平方向将图像分割成较小的区域，从而得到超像素。Veksler等人[10]提出的Compact Superpixels和Constant-Intensity Superpixels两种超像素分割算法（简称GCa和GCb）是基于同一全局能量模型下的两种变形，其基本思想是将相互重叠的图像块拼接起来，使任意像素只属于其中一个图像块。GCa和GCb算法各有优劣，前者生成紧密的超像素，而后者生成的超像素边缘贴合度较好。基于梯度下降的经典算法有Comaniciu等人[11]提出的MS02算法、Levinshtein等人[12]提出的TP09算法以及Achanta等人[13]提出的简单线性迭代聚类算法（simple linear iterative clustering，SLIC）。MS02算法通过定位密度函数的局部最大，对具有相同模点的像素进行聚类，实现超像素分割，该算法生成的超像素很不规则。TP09算法利用几何流的水平集方法，对初始化种子点进行逐步碰撞，实现超像素分割，该算法生成的超像素形状规则，但边缘贴合度较差。SLIC算法通过引入颜色距离和空间距离的相似性度量，采用简单的K-means聚类算法生成超像素。SLIC算法虽然能够生成较规则的超像素，但容易出现欠分割现象。

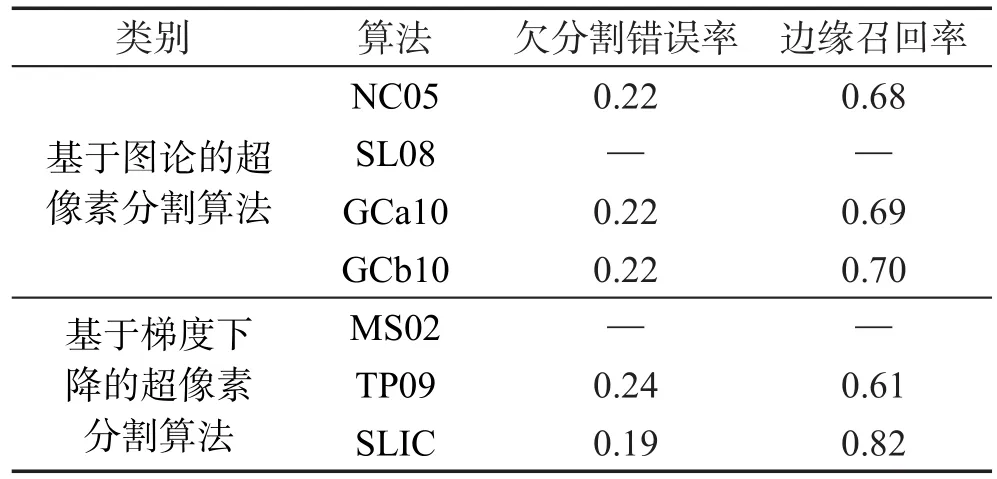
Table 1 Comparison of existing superpixel segmentation algorithms表1 现有超像素分割算法对比

虽然简单线性迭代聚类算法（SLIC）根据像素的颜色和距离特征进行聚类能实现良好的分割结果，但是存在如下几个问题：（1）SLIC算法实质上是K-means算法在特定场合的一种次优快速方案，K-means聚类的缺点是，算法要求先给出K值，但实际上K值很难估计。其次，算法根据原始聚类中心确定初始分割然后进行优化，而原始集群中心的选择影响聚类结果的稳定性，从而导致局部最优而非全局最优。（2）有限的超像素容易出现欠分割的情况。因此，本文提出一种新的算法WKK-SLIC，基于图像像素之间的颜色相似性和空间相似性度量，采用超像素分割的归一化割（normalized cuts）公式。不同于传统的基于特征的算法，WKK-SLIC算法使用核函数来近似相似性度量，将像素值和坐标映射到高维特征空间中，通过对该特征空间中的每个点赋予适当的权重，使加权K均值和归一化割的目标函数的优化在数学上等价。因此，可以通过在所提出的特征空间中迭代地应用简单的K-means聚类来优化归一化割的目标函数。同时，采用密度敏感的相似性度量计算空间像素点的密度，启发式地生成K-means聚类的初始中心以达到稳定的聚类结果。实验结果表明，WKK-SLIC算法在评估超像素分割的几个标准上优于SLIC算法。

2 SLIC超像素分割算法

简单线性迭代聚类算法的思想是在图像上均匀初始化K个初始聚类中心，将所有点赋予与其距离最近的聚类中心标签。SLIC算法默认只需要设定参数K，K是目标超像素数量。首先，根据K计算出超像素的平均长和宽，初始化超像素中心，让超像素中心初始值完全均匀地分布在整张图像上。若图片大小N为width×height，超像素的初始中心位置应该是网格状分布，长和宽方向上的步长分别为为了计算方便，算法设定超像素间的间隔长和宽方向都是这样会导致最右边和最下边的超像素初始覆盖半径很小。为了避免初始超像素中心落在物体边界，算法让每个超像素中心在当前3×3像素范围内找一个颜色梯度最小的种子位置，平移此超像素中心到其种子位置。初始的各个种子位置就是超像素的中心位置。同时，算法限定在超像素中心点2S×2S的区域搜索与中心点相似的像素而不是整个图像区域来提高算法的计算速度。每个像素点用五维空间中的一个点来表示，则像素点与超像素中心的相似性测量如下：

其中，dlab是CIELAB颜色空间中像素点之间的颜色距离；dxy是像素点间的空间距离；m是权衡颜色距离和空间距离重要性的一个常数参数。算法使用L2范数来计算当前超像素中心位置和新的超像素中心位置之间的残差误差E，重复迭代地更新超像素中心，直至误差E收敛，算法结束。

SLIC算法整体流程如下。

算法1SLIC超像素分割算法

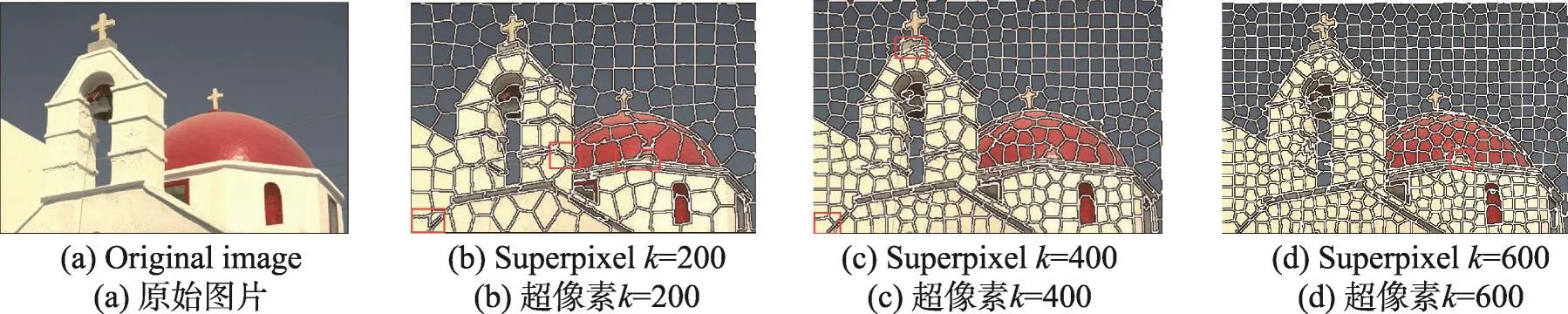
Fig.1 Segmentation results of SLIC algorithm图1 SLIC算法的分割结果

图1是使用SLIC算法进行图像分割的结果，其中（a）是原图BSD-118035，（b）～（d）分别表示目标超像素为200、400、600时的分割结果。图1显示，SLIC算法虽然能够产生较规则的超像素，但在有限的超像素数目内，SLIC算法容易出现欠分割的情况（图中用红色框标注的地方），且目标超像素数目越小欠分割现象越明显。

3WKK-SLIC算法

针对SLIC算法存在的缺陷，本文提出了一种基于优化加权核K-means聚类初始中心点的SLIC分割算法WKK-SLIC，算法基于图像像素之间的颜色相似性和空间相似性度量，采用超像素分割的归一化割公式。不同于传统的基于特征的算法，WKK-SLIC使用核函数来近似相似性度量，将像素值和坐标映射到高维特征空间中，通过对该特征空间中的每个点赋予适当的权重，加权K均值和归一化割的目标函数的优化在数学上等价。因此，可以通过在所提出的特征空间中迭代地应用简单的K-means聚类来优化归一化割的目标函数。同时，采用密度敏感的相似性度量计算空间像素点的密度，启发式地生成K-means聚类的初始中心以达到稳定的聚类结果。

3.1 引入核函数来近似相似性度量

WKK-SLIC算法以加权K-means聚类算法的目标函数和归一化割的目标函数之间的关系为基础。首先，回顾加权K-means聚类和归一化割的定义。用小写的p、q来表示输入空间中聚类的像素点，w(p)表示对应像素点赋予的权重，K表示聚类的数量，πk表示第k个聚类，ck表示第k个聚类的中心，φ表示将像素点映射到高维空间的函数，则加权核K-means的目标函数定义如下：

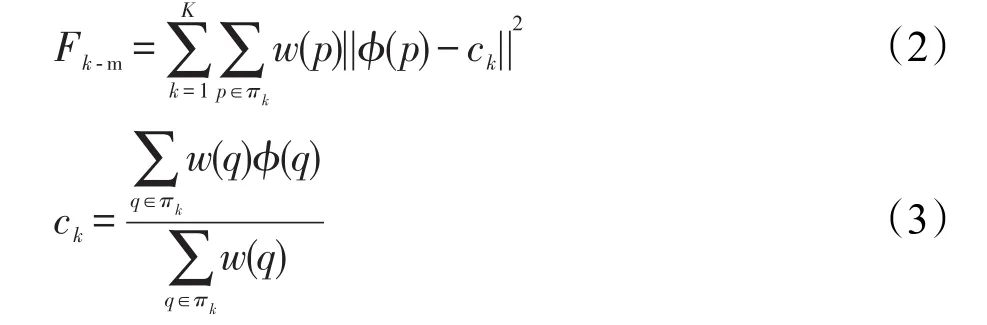
加权K-means的目标函数Fk-m可以通过迭代最小化。在归一化割中每个像素点用图G=(V,E,W)中的节点来表示，其中V是所有节点的集合，E是所有边的集合，是像素点间的相似性函数。归一化割的目的是最大化目标函数FNcuts。FNcuts的定义如下：

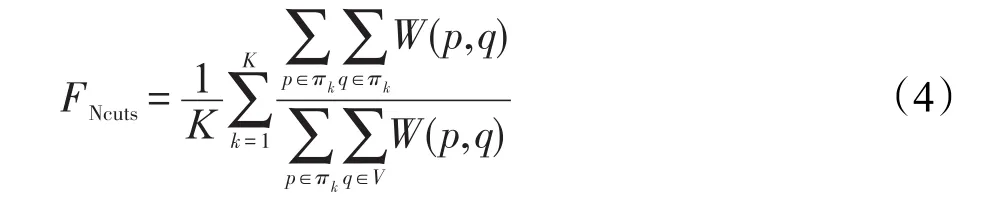
为了进一步了解Fk-m和FNcuts之间的关系，引入推论1。其中，式（5）和式（6）可由文献[14]的结果推导得到。

推论1如果式（5）和式（6）成立，则加权K-means和归一化割的目标函数的优化在数学上是等价的。

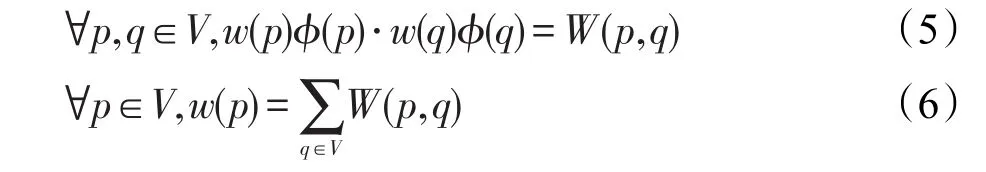
式（5）表示，高维特征空间中两个向量的加权内积等于输入空间中两个对应点之间的相似性。式（6）表示加权K-means聚类中的每个像素点的权重等于对应的归一化割中该点与其他所有节点的边的权重的总和。在推论1的两个充分条件中，式（6）可以通过归一化割中边的权重的总和作为加权K-means中的点的权重来实现，然而对于式（5），需要仔细选择相似性函数。将式（5）重写为式（7）：

式（7）实际上定义了一个对称的核函数，因此它必须满足对应的核矩阵总是半正定的条件。本文用(l,a,b,x,y)五维向量来表示图像中的每个像素点，为了方便，限定每个变量的范围在[0,1]。在CIELAB颜色空间，定义两个像素点之间的相似性度量，如式（8）所示，其中Cs和Cc是衡量空间距离和颜色距离重要性的常系数。式（8）可以写成式（5）的内积形式，其中φ和w分别定义为式（9）和式（10）：

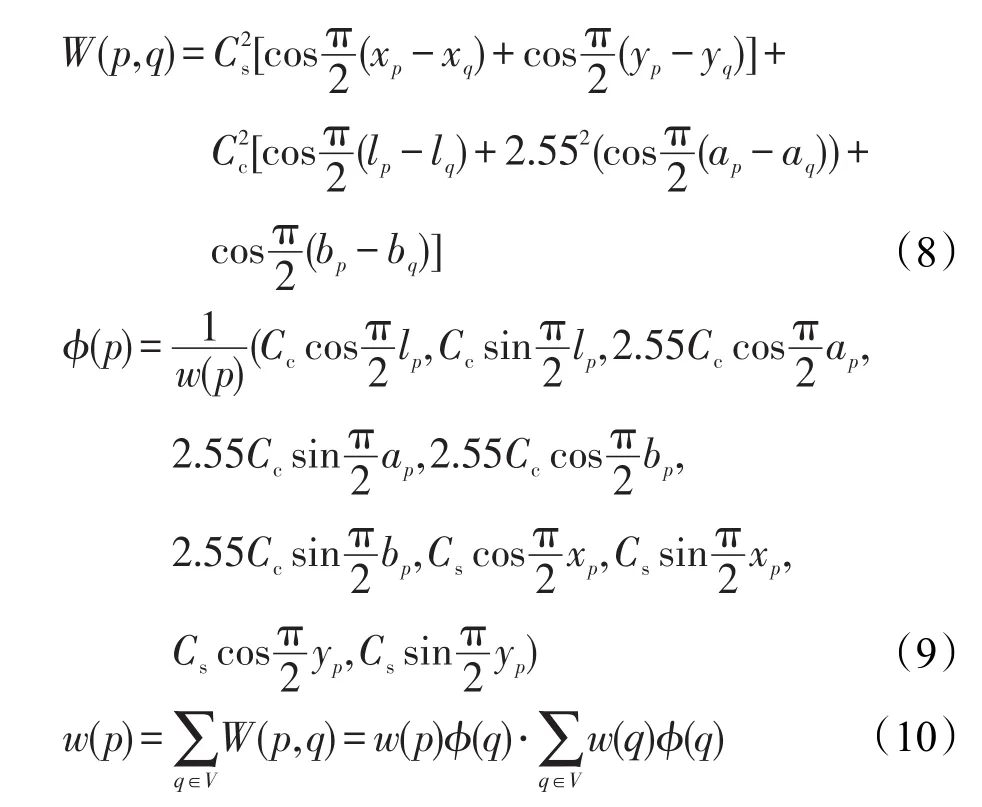
选择CIELAB颜色空间是因为欧几里得距离在该空间中几乎是均匀的。另外，选用余弦函数作为相似性度量函数是因为使用余弦函数定义的相似性函数W(p,q)能够满足式（7）所要求的对应核函数矩阵半正定的要求，φ和w也是根据此进行定义。到此，本文定义了十维的特征空间，使得加权K-means聚类在该特征空间中近似等价于输入空间中的归一化割。通过在该十维特征空间中直接应用加权K-means，可以有效地优化归一化割的目标函数，达到全局的稳定的聚类结果。

3.2 结合密度敏感的相似性度量启发地生成K-means聚类中心

SLIC算法实质上是K-means算法在特定场合的一种次优快速方案。原始的K-means算法存在如下缺陷：

（1）算法要求事先给定K值，但实际上K值一般很难确定；

（2）对初始聚类中心敏感，不同的初始中心可能会导致不同的聚类结果。

以上缺陷导致SLIC算法生成的超像素不稳定，容易出现欠分割的情况。因此，本文结合密度敏感的相似性度量来计算图像像素点的密度，启发地生成初始聚类中心。下面给出相关的定义[15]。

定义1（聚类对象的密度）对于图像上的像素点，定义pi的密度为：

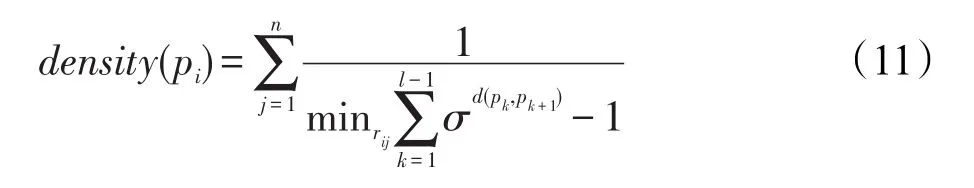
其中，d(pk,pk+1)表示对象pk、pk+1的欧式距离；σ为密度参数；rij为链接像素点pi和pj之间的所有路径；l代表链接像素点pi和pj路径中像素点的个数。

定义2（聚类对象的邻域）对于任意像素点p，以p为中心，R为半径的圆形区域，称该区域为像素点p的邻域，记为：

定义3（聚类对象的邻域半径）

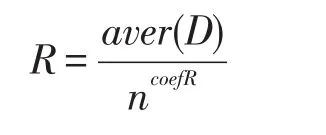
其中，aver(D)表示所有像素点间距离的平均值；n是图像像素点的总数；coefR是邻域半径调节系数。

基于密度初始化中心点算法的基本思想是首先在图像上所有像素点集N中选择密度最大的像素点作为第一个初始中心，然后在像素点集中去除该像素点及其邻域内的所有像素点，再按同样的方法确定第二个初始中心点，循环直达初始中心点集M中有K个点。算法描述如下。

算法2基于密度的初始化中心点算法

1.根据定义1计算所有像素点的密度density(pi)，初始化中心点集M={}。

2.选择密度最大的像素点Pmax={pi|pi∈N,i=1,2,…,n}作为第一个初始中心点，添加到中心点集M中，M=M⋃{Pmax}，并从像素点集中删去该对象，即N=N-{Pmax}。根据定义2和定义3计算Pmax邻域内的所有像素点，并从像素点集N中删去。

3.重复执行步骤2，直到初始中心点集中有K个中心点，即|M|=K。

4.输出初始中心点集M，算法结束。

3.3 基于优化加权核K-means聚类初始中心点的SLIC分割算法

在SLIC算法框架的基础上，结合3.1节和3.2节的内容，基于优化加权核K-means聚类初始中心点的SLIC分割算法（WKK-SLIC）的描述如下。

算法3WKK-SLIC算法

4 实验结果与分析

WKK-SLIC算法的分割结果如图2所示，其中（a）是原图BSD-118035，（b）～（d）分别表示目标超像素为200、400、600时的分割结果。可以看出，与SLIC算法相比，WKK-SLIC算法不仅能生成规则的超像素，且在有限的超像素数内没有出现欠分割的现象。

为了进一步比较，在Berkeley Segmentation Database公共数据集上进行实验。采用边缘贴合度标准，包括边缘召回率和欠分割错误率，来评估算法性能。WKK-SLIC算法和SLIC算法性能对比结果如图3所示。

边缘召回率指落在至少一个真值边缘像素点距离ε（通常ε取两个像素）范围内的超像素边缘像素点数量与真值边缘像素点总数的比值，边缘召回率越高，生成的超像素越规则。本文采用文献[16]中的边缘召回率计算方法。

欠分割错误率衡量了超像素区域“溢出”真值区域边界的比例，欠分割错误率越低，生成的超像素越纯洁。由于处理不同区域间边缘像素的方法不同，目前该标准存在多种计算模型[17]，本文采用的是文献[18]提出的CUE（corrected under-segmentation error）计算模型。

Fig.2 Segmentation results of WKK-SLIC algorithm图2WKK-SLIC算法的分割结果

Fig.3 Performance comparison results of WKK-SLIC algorithm and SLIC algorithm图3WKK-SLIC算法和SLIC算法的性能对比结果

图3（a）显示对于不同数目的目标超像素，WKKSLIC算法比原始的SLIC算法有更低的欠分割错误率。图3（b）显示对于不同数目的目标超像素，WKKSLIC算法比原始的SLIC算法有更高的边缘召回率。

5 结束语

本文在原始SLIC算法框架的基础上，将图像像素点映射到高维空间，引入核函数来近似像素相似性度量，同时使用基于密度的初始化中心点算法来初始化聚类中心，提出一种基于优化加权核K-means聚类初始中心点的SLIC分割算法WKK-SLIC。该算法生成的超像素规则且分割结果能够保持图像的全局属性。实验结果表明，WKK-SLIC算法在超像素分割中几个常用的评价标准方面优于SLIC算法。

[1]Ren Xiaofeng,Malik J.Learning a classification model for segmentation[C]//Proceedings of the 9th International Conference on Computer Vision,Nice,Oct 13-16,2003.Washington:IEEE Computer Society,2003,1:10-17.

[2]Achanta R,Shaji A,Smith K,et al.SLIC superpixels compared to state-of-the-art superpixel methods[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2012,34(11):2274-2282.

[3]Wang Chunyao,Chen Junzhou,Li Wei.Review on superpixel segmentation algorithms[J].Application Research of Computers,2014,31(1):6-12.

[4]Xu Chenliang,Corso J J.Evaluation of super-voxel methods for early video processing[C]//Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition,Providence,Jun 16-21,2012.Washington:IEEE Computer Society,2012:1202-1209.

[5]Rao Qian,Wen Hong,Yu Wen,et al.Review about superpixels and its applications[J].Computer and Information Technology,2013,21(5):1-3.

[6]Zhu Fengqing,Bosch M,Khanna N,et al.Multiple hypotheses image segmentation and classification with application to dietary assessment[J].IEEE Journal of Biomedical and Health Informatics,2015,19(1):377-388.

[7]Felzenszwalb P F,Huttenlocher D P.Efficient graph-based image segmentation[J].International Journal of Computer Vision,2004,59(2):167-181.

[8]Harary S,Kropf N S,Marder M,et al.Image segmentation:US,Patent 9,300,828[P].2016-03-29.

[9]Moore A P,Prince S J D,Warrell J,et al.Superpixel lattices[C]//Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition,Anchorage,Jun 23-28,2008.Washington:IEEE Computer Society,2008:1-8.

[10]Veksler O,Boykov Y,Mehrani P.Superpixels and supervoxels in an energy optimization framework[C]//LNCS 6315:Proceedings of the 11th European Conference on Computer Vision,Heraklion,Sep 5-11,2010.Berlin,Heidelberg:Springer,2010:211-224.

[11]Comaniciu D,Meer P.Mean shift:a robust approach toward feature space analysis[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(5):603-619.

[12]Levinshtein A,Stere A,Kutulakos K N,et al.TurboPixels:fast superpixels using geometric flows[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009,31(12):2290-2297.

[13]Achanta R,Shaji A,Smith K,et al.SLIC superpixels,149300[R].2010.

[14]Dhillon I S,Guan Yuqiang,Kulis B.Weighted graph cuts without eigenvectors a multilevel approach[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(11):1944-1957.

[15]Wang Zhong,Liu Guiquan,Chen Enhong.AK-means algorithm based on optimized initial center points[J].Pattern Recognition andArtificial Intelligence,2009,22(2):299-304.[16]Van den Bergh M,Boix X,Roig G,et al.SEEDS:superpixels extracted via energy-driven sampling[C]//LNCS 7578:Proceedings of the 12th European Conference on Computer Vision,Florence,Oct 7-13,2012.Berlin,Heidelberg:Springer,2012:13-26.

[17]Neubert P,Protzel P.Superpixel benchmark and comparison[C]//Proceedings of Forum Bildverarbeitung,Karlsruhe,2012:1-12.

[18]Buyssens P,Gardin I,Ruan Su,et al.Eikonal-based region growing for efficient clustering[J].Image and Vision Computing,2014,32(12):1045-1054.

附中文参考文献：

[3]王春瑶,陈俊周,李炜.超像素分割算法研究综述[J].计算机应用研究,2014,31(1):6-12.

[5]饶倩,文红,喻文,等.超像素及其应用综述[J].电脑与信息技术,2013,21(5):1-3.

[15]汪中,刘贵全,陈恩红.一种优化初始中心点K-means算法[J].模式识别与人工智能,2009,22(2):299-304.