4类平面多项式微分系统的Lyapunov量复算法
, , ,
(1. 黄淮学院 数学与统计学院, 河南 驻马店 463000; 2. 信阳师范学院 数学与统计学院, 河南 信阳 464000; 3. 北京工业大学 应用数理学院, 北京 100124)
Lyapunov量及其等价的焦点量在微分方程的定性理论和分岔理论中非常重要,可以用于判断微分方程的稳定性,并且与极限环的研究联系紧密。借助于计算软件进行Lyapunov量的计算,可以判断原点是否为细焦点或中心。文献[1-3]中系统地研究了Lyapunov量的一些性质。文献[2]中主要研究了计算一类平面多项式系统Lyapunov量的复算法以及判断中心的方法,并使用符号计算软件进行实例分析。文献[4-5]中研究2类平面多项式系统到基本形式的转换, 拓宽了文献[2]中的研究范围,给出计算Lyapunov量的计算流程。文献[6]中研究了一类三次系统的中心判定问题,证明了该系统以原点为中心的充要条件是其前五阶焦点量全为0。文献[7]中研究了2类一致等时系统的小振幅极限环分支问题,证明了从细焦点分支出小振幅极限环。在文献[1-5]中研究的基础上,文献[8-11]中对平面多项式系统的Lyapunov量复算法进行了深入探讨。文献[12-13]中讨论一类四次多项式微分系统的中心条件与极限环分支问题,通过对系统所对应的伴随复系统奇点量的计算,得到系统的原点成为中心和细焦点的条件。文献[14-15]中通过研究受扰平面的Hamilton向量场,得到了尽可能多的极限环及其分布构型的方法。
本文中分别讨论2类四次平面多项式微分系统和加单扰动项、双扰动项的2类多项式微分系统的Lyapunov量复算法,通过计算相应系统的Lyapunov量,分析系统在原点的中心焦点问题,在文献[12-15]中结果的基础上给出原点成为中心和细焦点类型的证明,并判断在具体参数控制下的细焦点的稳定性。
1 Lyapunov量复算法
由文献[2],可得相关理论基础。平面多项式系统形式为

(1a)
式中:x,y∈;f(x,y)和g(x,y)为解析函数。 当x2+y2→0时,有
f(x,y)=O(x2+y2),
g(x,y)=O(x2+y2)。
式(1a)对应的复系统为
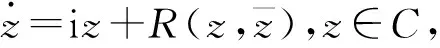
(1b)
式中:z=x+iy;
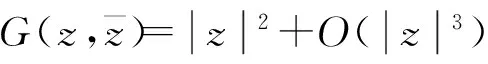
(2)
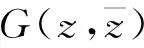
性质1[10]如果所有的Lyapunov量都为0,则原点是式(1a)的中心;否则是细焦点;如果Lk是第1个非零的Lyapunov量,则称原点为k阶细焦点。
性质2[10]如果Lk<0,则原点是稳定的;如果Lk>0,则原点不稳定。
2 第1类四次平面多项式微分系统的Lyapunov量复算法
主要计算第1类四次平面多项式微分系统的Lyapunov量,研究系统在原点的中心焦点判定问题。第1类四次平面多项式微分系统[12]形式为
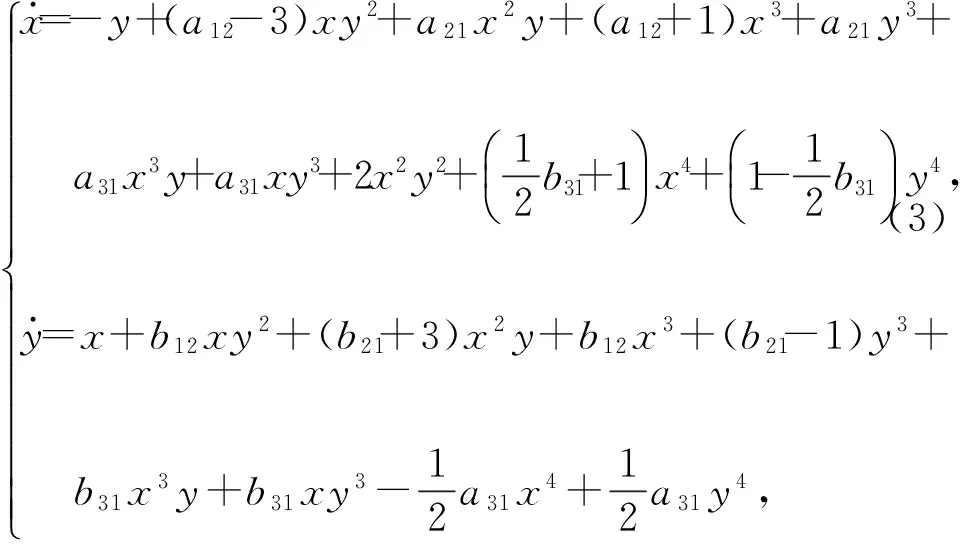
x·=-y+(a12-3)xy2+a21x2y+(a12+1)x3+a21y3+a31x3y+a31xy3+2x2y2+12b31+1æèçöø÷x4+1-12b31æèçöø÷y4,y·=x+b12xy2+(b21+3)x2y+b12x3+(b21-1)y3+b31x3y+b31xy3-12a31x4+12a31y4,ìîíïïïïïïïïïïïï(3)
式中aij、bij(i,j=1,2,3)均为实数。
令z=x+iy,系统(3)转换为如下复形式:
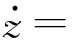
(4)
利用Lyapunov量的复算法, 借助数学计算工具, 可以求出系统(4)的Lyapunov量, 具体步骤如下:L1=a12+b21;L2=-a21-b12(L1=0,此时b21=-a12);L3=a31(L1=L2=0,此时b21=-a12,b12=-a21);L4=2a12(b31+1)-2(L1=L2=L3=0,此时b21=-a12,b12=-a21,a31=0)。
根据文献[2, 5, 11]中的相关理论, 可得如下2个结论。
结论1 原点成为系统(3)的中心所满足的条件为b21=-a12,b12=-a21,a31=0,b31=(1-a12)/a12,a12≠0。
证明: 当满足b21=-a12,b12=-a21,a31=0,b31=(1-a12)/a12,a12≠0这些条件时,L1=L2=L3=L4=…=0,因此原点为系统的中心。
结论2 原点成为系统(3)的最高阶细焦点的阶数为4。
证明: 当且仅当b21=-a12时,L1=0; 当且仅当b21=-a12,b12=-a21时,L1=L2=0; 当且仅当b21=-a12,b12=-a21,a31=0时,L1=L2=L3=0;当且仅当b21=-a12,b12=-a21,a31=0,a12(b31+1)=1时,L1=L2=L3=L4=…=0; 因此, 只有在满足b21=-a12,b12=-a21,a31=0,a12(b31+1)≠1这些条件时,L1=L2=L3=0,L4=2a12(b31+1)-2≠0,此时原点成为系统(3)的最高阶细焦点,阶数为4。
下面给出一组数值进行模拟。取b21=-a12=-2.4,b12=-a21=2,a31=0,b31=1.2,此时系统(3)具有形式
(5)
通过计算,L1=L2=L3=0,L4=8.56>0,此时原点是不稳定的四阶细焦点。
3 第2类四次平面多项式微分系统的Lyapunov量复算法
主要计算第2类四次平面多项式微分系统的Lyapunov量,研究系统在原点的中心焦点判定问题。第2类四次平面多项式微分系统[13]形式为
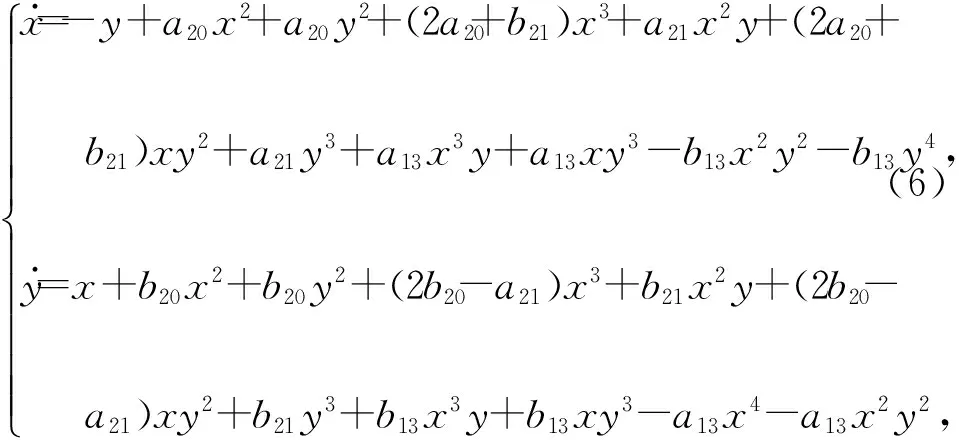
x·=-y+a20x2+a20y2+(2a20+b21)x3+a21x2y+(2a20+b21)xy2+a21y3+a13x3y+a13xy3-b13x2y2-b13y4,y·=x+b20x2+b20y2+(2b20-a21)x3+b21x2y+(2b20-a21)xy2+b21y3+b13x3y+b13xy3-a13x4-a13x2y2,ìîíïïïïïïïïïï(6)
式中aij、bij均为实数。
令z=x+iy,系统(6)转换为复形式

(7)

根据文献[2,5,11]中的相关理论可得如下2个结论。
结论3 原点成为系统(6)的中心所满足的条件如下:
1)b21=-a20,b20=a13a20/b13,b13≠0,a20=0;
2)b21=-a20,b13=0,a20=0;
3)b21=-a20,b13=0,a13=0。
证明:当分别满足条件1)、 2)、 3)时,L1=L2=L3=L4=…=0,因此,原点是系统(6)的中心。
结论4 原点成为系统(6)的最高阶细焦点的阶数为3。
证明:1)当b21=-a20时L1=0;当b21=-a20,b20=a13a20/b13,b13≠0时,L1=L2=0; 当b21=-a20,b20=a13a20/b13,b13≠0,a20=0,L1=L2=L3=L4=…=0。
2)当b21=-a20时L1=0;当b21=-a20,b13=0,a20=0时,L1=L2=L3=L4=…=0。
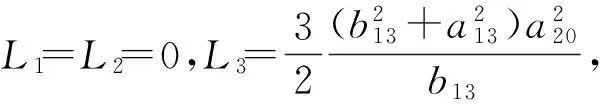
下面给出一组数值进行模拟。取b21=-a20=2.4,a21=1,a13=3.6,b13=-2,b20=4.32,此时系统(6)具有形式
(8)
通过计算,L1=L2=0,L3=-73.27<0,此时原点是稳定的三阶细焦点。
4 第3类加单扰动项的多项式微分系统的Lyapunov量复算法
讨论加1个扰动项的多项式微分系统[14]
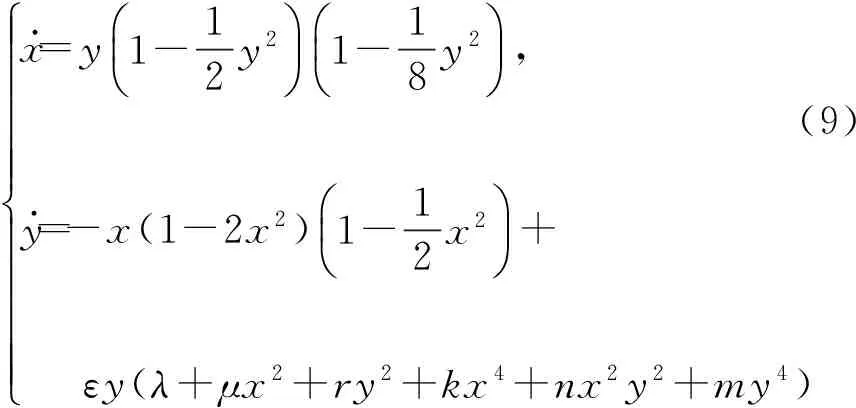
x·=y1-12y2æèçöø÷1-18y2æèçöø÷,y·=-x(1-2x2)1-12x2æèçöø÷+εy(λ+μx2+ry2+kx4+nx2y2+my4)ìîíïïïïïïïïïï(9)
的Lyapunov量复算法问题, 其中0<ε≪1,λ=0,m=1,μ、r、k、n为参数。
系统(9)可简化为

x·=y1-12y2æèçöø÷1-18y2æèçöø÷,y·=-x(1-2x2)1-12x2æèçöø÷+εy(μx2+ry2+kx4+nx2y2+y4)。ìîíïïïïïïïïïï(10)
讨论单扰动系统(10)在以下2组控制条件下的中心和细焦点问题。
1)在第1组控制条件下, 系统的扰动参数组为(μ,r,k,n)=(55.578 506 73, -15.438 847 42, 3.123 873 423,-2.604 067 373)。在该组控制条件下,求出系统(10)的Lyapunov量为L1=-2.315 49ε,L2=-12.630 8ε,L3=-13.081 28ε-235.556 36ε3,L4=7.079 179ε-3 825.635 8ε3,…。
当ε=0时,L1=L2=L3=…=0,此时原点为系统(10)的中心。
如果取ε=0.01, 则L1<0,L2<0,L3<0,L4>4,L5>0……, 此时原点为系统(10)的一阶稳定细焦点。
2)在第2组控制条件下,系统的扰动参数组为
(μ,r,k,n)=(-2.519 836 620, -17.038 846 67, -35.999 344 34, 3.150 348 690)。在该组控制条件下,求出系统(10)的Lyapunov量为L1=15.559 097ε,L2=-1.997 08ε,L3=-22.026 57ε-4 757.026ε3,L4=-71.594 0ε-10 650.573ε3,…。
当ε=0时,L1=L2=L3=…=0,此时原点为系统(10)的中心。
如果取ε=0.01,L1>0,L2<0,L3<0,L4<0,L5<0,…, 此时原点为系统(10)的一阶不稳定细焦点。
5 第4类加双扰动项的多项式微分系统的Lyapunov量复算法
讨论加2个扰动项的多项式微分系统[15]
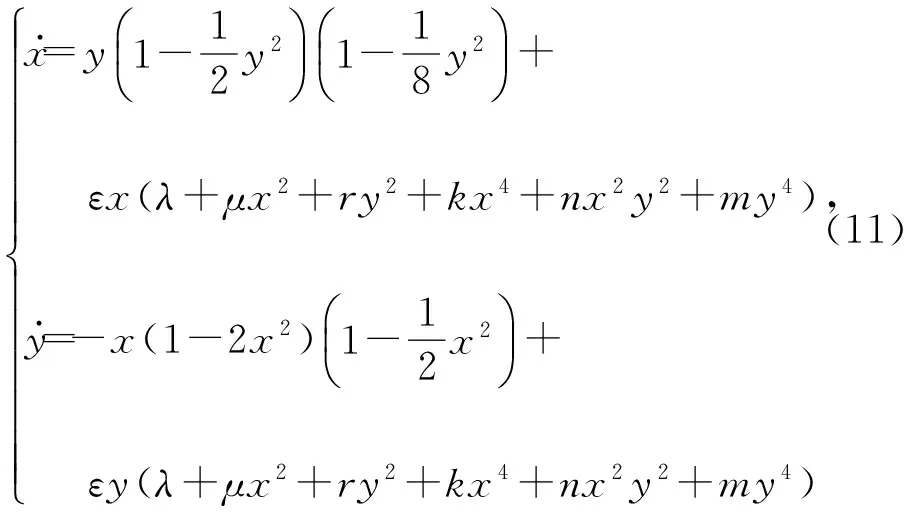
x·=y1-12y2æèçöø÷1-18y2æèçöø÷+εx(λ+μx2+ry2+kx4+nx2y2+my4),y·=-x(1-2x2)1-12x2æèçöø÷+εy(λ+μx2+ry2+kx4+nx2y2+my4)ìîíïïïïïïïïïïïï(11)
的Lyapunov量复算法问题, 其中0<ε≤1,λ=0,m=1,μ、r、k、n为参数。
系统(11)可简化为

x·=y1-12y2æèçöø÷1-18y2æèçöø÷+εx(μx2+ry2+kx4+nx2y2+y4),y·=-x(1-2x2)1-12x2æèçöø÷+εy(μx2+ry2+kx4+nx2y2+y4)。ìîíïïïïïïïïïïïï(12)
讨论双扰动系统(12)在以下2组控制条件下的中心和细焦点问题。
1)在第1组控制条件下,系统的扰动参数组为
(μ,r,k,n,m)=(-0.924,-6.830 26,-3.112 99,1.7, 0.415 312 5)。在该组控制条件下,求出系统(12)的Lyapunov量为L1=7.754 26ε,L2=-1.170 30ε,L3=-10.926 2ε-202.874 1ε3,L4=-35.280 7ε-220.579 8ε3,…。
当ε=0时,L1=L2=L3=…=0,此时原点为系统(12)的中心。
如果取ε=0.01,L1>0,L2<0,L3<0,L4<0,L5<0, …, 此时原点为系统(12)的一阶不稳定细焦点。
2)在第2组控制条件下,系统的扰动参数组为
(μ,r,k,n,m)=(-12.805 773, 10.671 735 4, -0.479 846 23, 1.2, -0.768 029)。在该组控制条件下, 求出系统(12)的Lyapunov量为L1=23.477 5ε,L2=1.636 2ε,L3=-28.946ε-80.189ε3,L4=-109.85ε-1 149.661ε3,…。
当ε=0时,L1=L2=L3=…=0,此时原点为系统(12)的中心。
如果取ε=0.01,L1>0,L2>0,L3<0,L4<0,L5<0,…,此时原点为系统(12)的一阶不稳定细焦点。
6 结论
本文中主要探讨了4类平面多项式微分系统的Lyapunov量复算法。计算出前2类平面多项式微分系统的Lyapunov量,得到2类四次系统的原点成为中心的充分条件和原点成为系统最高阶细焦点的阶数,阶数分别为4和3。最后取定参数值探讨了具体情况下的系统的最高阶细焦点的稳定性;讨论了在几组不同的控制参数组下,加单扰动项和双扰动项的后2类系统的Lyapunov量复算法。
[1] WANG D. A recursive formula and its application to computations of normal forms and focal values[M]//LIAO S T. Dynamical Systems. Singapore: World Sci Publ, 1993: 238-247.
[2] WANG D, MAO R. A complex algorithm for computing Lyapunov values[J]. Random & Comput Dyn, 1994,2(2/3):261-277.
[3] WANG D, MAO R. Jumping property of Lyapunov values[J]. Science in China, 1996,39(12):1280-1287.
[4] LI J, CHEN Y, ZHANG W. The complex algorithm for computing Lyapunov values for two planar polynomial systems[C]//中国力学学会.第二届国际动力学、振动与控制学术会议论文集. 北京:中国力学学会, 2006:27.
[5] LI J, CHEN Y, ZHANG W,et al. Computation of Lyapunov va-lues for two planar polynomial differential systems[J]. Appl Math & Comput, 2008, 204(1):240-248.
[6] 桑波.一类三次系统的中心判定问题[J].数学年刊:A辑,2014, 35(3):361-372.
[7] 桑波.两类一致等时系统的小振幅极限环分支[J].系统科学与数学, 2016, 36(5):728-735.
[8] 陈莹,李静.Bautin系统的Lyapunov量复算法[J].力学季刊, 2009, 309(1):88-91.
[9] 陈莹,师建国,李静. 托卡马克装置三次系统的Lyapunov量计算[J].扬州大学学报(自然科学版),2010,13(1):10-12.
[10] 陈莹,彭真,李静. 两类五次平面多项式系统的中心判定[J].河南科技大学学报(自然科学版),2012,33(3) :70-74.
[11] 陈莹,李小朝,李静. Lyapunov量复算法对细焦点和中心的判定的研究[J].山西大学学报(自然科学版), 2012, 35(4): 613-619.
[12] 赵大虎,卢景苹.一类四次多项式系统原点的中心条件与极限环分支[J].黑龙江大学自然科学学报,2012,29(6):767-770.
[13] 卢景苹.一类四次多项式系统原点的极限环分支[J].广西科学,2013,20(2):85-87.
[14] LI J. Hilbert’s 16th problem and bifurcations of planar poly-nomial vector fields[J]. International Journal of Bifurcation and Chaos,2003,13:47-106.
[15] LI J , CHAN H S Y, CHUNG K W. Investigations of bifurcation of limit cycles inZ2-equivariant planar vector field of degree 5[J]. International Journal of Bifurcation and Chaos,2002,12:2137-2157.

