二维二阶常系数双曲型方程的参数估计方法
,
(东北林业大学 理学院, 黑龙江 哈尔滨 150036)
双曲型偏微分方程是描述振动或波动现象的一类偏微分方程, 双曲型偏微分方程的参数估计问题广泛存在于自然科学和工程技术领域中[1], 因此研究双曲型偏微分方程的参数估计方法在理论和实际方面都具有重要意义。 关于双曲型方程的参数估计方法的研究已有一些进展, 如差分演化算法[1-6]、 最佳摄动量法[7-8]、 遗传算法[9-10]等。 在理论上最完备而且行之有效的方法, 是由前苏联科学家Tikhonov以第一类算子方程为基本框架于20世纪60年代初创造性提出且后来得到深入发展的正则化方法[11-12], 但是它也有一定的局限性,例如正则化参数的选择困难、 代步数的难以确定、 通用性的缺乏等。虽然双曲线型方程的参数估计方法多种多样,但是多数都处于理论计算阶段,应用到实际中的效果并不理想,并且一种方法大多都只能针对一类问题;因此研究新理论、 探索新方法是必要的,特别是通过采样数据来估算方程中参数的方法颇具实际意义。本文中从新的角度出发,在仅已知模型类型和观测数据的条件下,将偏微分中的数值差分思想与最小二乘理论[13]结合,给出一种常系数非齐次双曲型方程的参数估计方法,并通过实例模拟来验证该方法的可行性。
1 理论推导
含2个自变量x、y和未知函数u的二阶线性常系数偏微分方程的一般形式为
Auxx+Buxy+Cuyy+Dux+Euy+Fu=g(x,y),
(1)
式中:A、B、C、D、E、F为常数;g(x,y)为已知函数。当B2-4AC>0时,该方程为双曲型方程[14]。
将u(x,y)在区域[a,b]×[c,d](其中a、b、c、d均大于或等于0)分别取步长h1和h2作2族与x轴、y轴平行的直线,得到矩形网格,2族直线的交点(a+ih1,c+jh2)称为网点或节点[15],记为(xi,yj)或(i,j),节点处的函数值记为u(xi,yj)或uij(i,j=1,2,…)。
给定一组数据(u(k)(xi-1,yj),u(k)(xi,yj-1),u(k)(xi,yj),u(k)(xi,yj+1),u(k)(xi+1,yj),u(k)(xi+1,yj+1),g(k)(xi,yj)),k=1,2,…,N,N∈+,令
(2)
得到一组数据
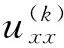
(3)
方程(1)变为差分方程
Fu(xi,yj)=g(xi,yj)。
(4)
方程(4)可以看作预测模型,在已知参数A、B、C、D、E、F的条件下,可以利用u(xi-1,yj)、u(xi,yj-1)、u(xi,yj)、u(xi,yj+1)、u(xi+1,yj)的值,估算u(xi+1,yj+1)的值。
将方程(1)看作多元线性函数,则把二阶二维常系数双曲型方程的参数估计问题转化成线性回归模型的参数估计问题,下面估计A、B、C、D、E、F的值。
设有N组数据(3),利用最小二乘原理,令
Y=Xβ+e,
E(e)=0,

Y′Y=2Y′Xβ+β′X′Xβ,
Cov(e)=σ2In,
式中:σ为常数;In为n阶单位矩阵,n∈+。
对β求偏导,并令其为0,得
X′Xβ=X′Y。
当方程(1)的解u(x,y)为非二次及二次以下的代数多项式时,|X′X|一定不为0,因此X′X是可逆的,从而得到参数β的估计值
(5)
2 数值模拟与验证
为了验证上述方法的有效性,以双曲型方程初值问题
(6)
为例,对其参数进行估计及数值模拟。
通过计算可知,上述双曲型方程的解为
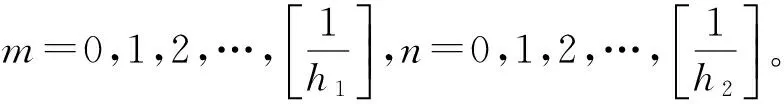

利用这N组数据,根据第1节中给出的方法来验证估算方程(6)中的参数,以此验证第1节中方法的有效性。
设有方程
Auxx+Buxy+Cuyy+Dux+Euy+Fu=xy,
(7)
利用N组数据估算A、B、C、D、E、F的估计值。
设h1=h2=h, 利用式(5), 得出方程(7)中各参数的估计值, 见表1。 由表可知, 当h→0时,A→1,B→3,C→2,D→0,E→0,F→0,因此方程(7)可以转化为
Auxx+Buxy+Cuyy=xy。
(8)
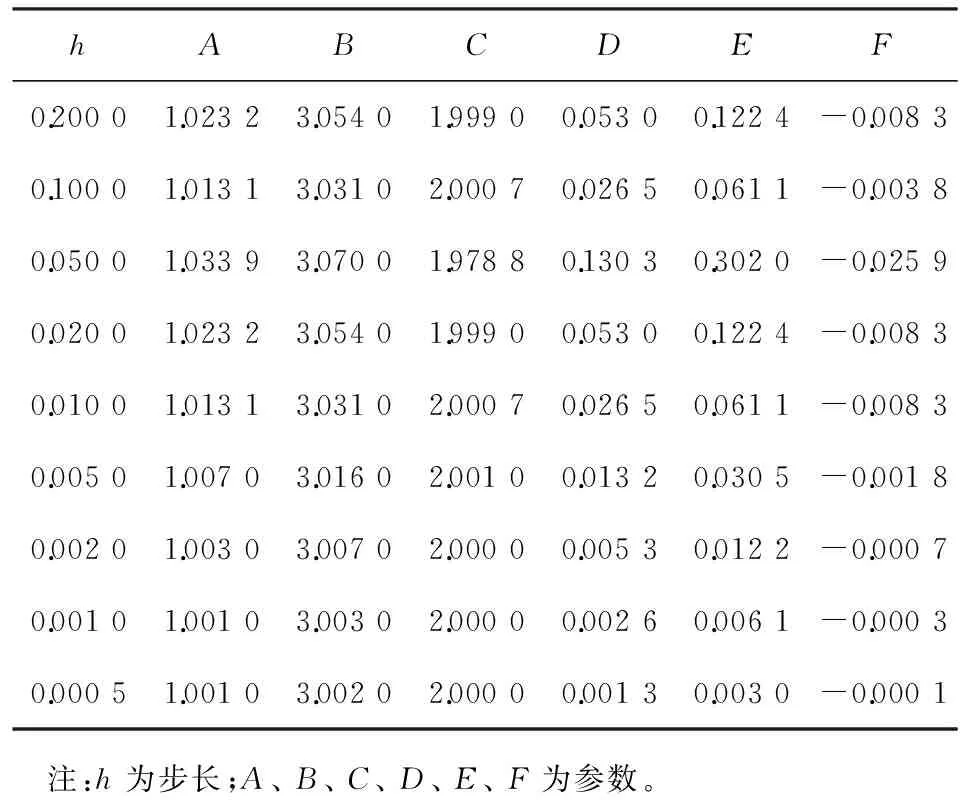
表1 方程(7)中各参数的估计值
下面分3种情况讨论方程(8)中各参数的估计值。
1)当h1=h2=h时,利用式(5),得到方程(8)中A、B、C的估计值, 见表2。 由表可知, 当步长h≤0.05时, 可以较准确地估计出前面双曲型方程(6)中的参数。 图1所示为各参数估计值的相对误差与步长h的关系。 由图可知,h越小, 方程各参数的相对误差也越小, 当h<0.05时,A的相对误差小于0.4,B的相对误差小于0.4,C的相对误差小于0.2。这说明第1节中给出的方法是有效的。
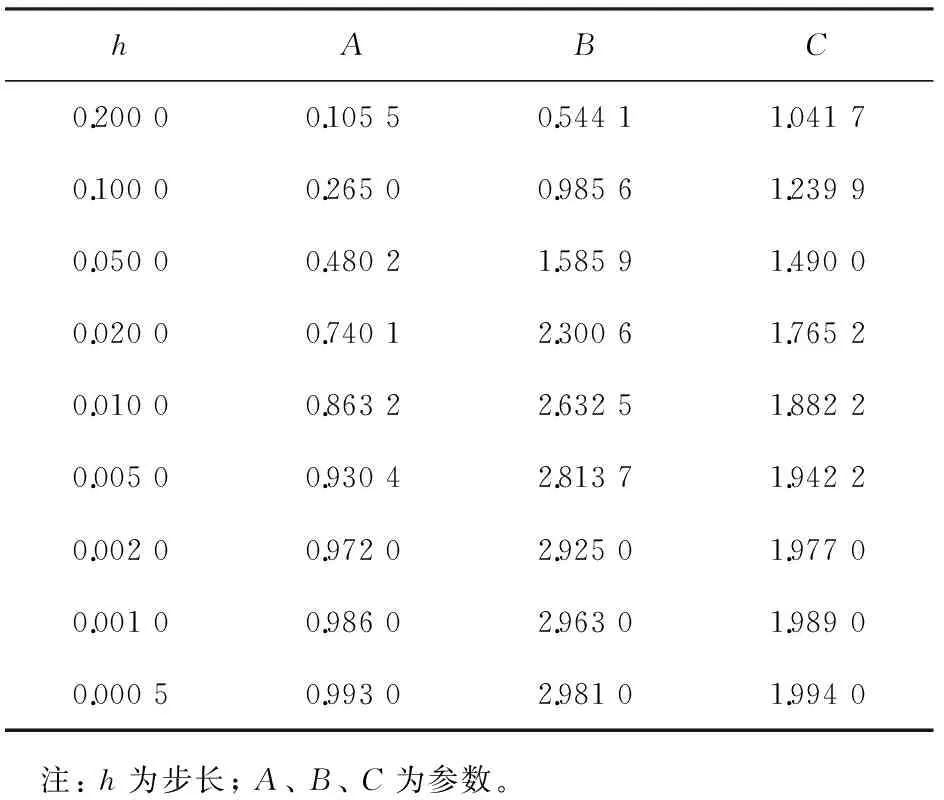
表2 在步长h1=h2的条件下方程(8)中各参数的估计值

(a)参数A(b)参数B(c)参数C图1 在步长h1=h2的条件下各参数的相对误差与步长h的关系
2)固定h1=0.01,利用式(5)得出方程(8)中参数A、B、C的估计值,见表3。图2所示为各参数的相对误差与步长h2的关系。由表3、图2可知,当固定h1=0.01时,并不是h2越小,A、B、C的相对误差越小,而是h1和h2满足一定关系时,A、B、C的估计值越接近真实值。当h2是h1的2~3倍时,A、B、C的估计值更准确。

表3 在步长h1=0.01的条件下方程(8)中各参数的估计值

(a)参数A(b)参数B(c)参数C图2 在步长h1=0.01的条件下各参数的相对误差与步长h2的关系
3)固定h2=0.01,利用式(5)得出方程(8)中参数A、B、C的估计值,见表4。图3所示为各参数的相对误差与步长h1的关系。由表4、图3可知,当固定h2=0.01时,h2越小,A、B、C的相对误差也并非越小,而是h1和h2满足一定关系时,A、B、C的估计值越接近真实值。
3 结论与讨论
1)将数值差分思想与最小二乘理论结合,给出一种二阶常系数非齐次双曲型方程的参数估计方法,即利用依次采样数据估算二阶常系数非齐次双曲型方程中的参数。如果双曲型方程的解为非二次及低于二次的代数多项式,则本文中的方法具有可行性,并通过实例验证了该方法是可行的。
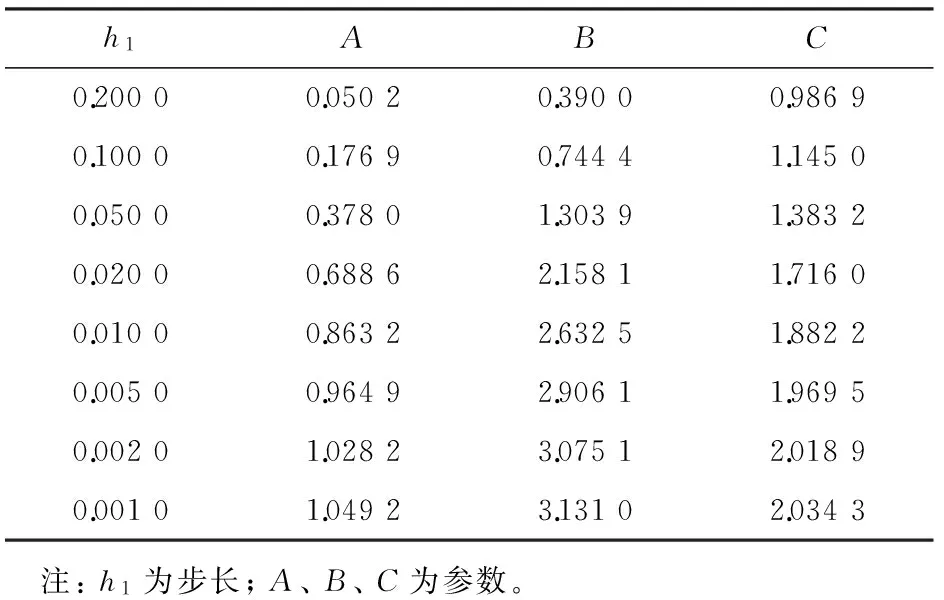
表4 在步长h2=0.01的条件下方程(8)中各参数的估计值

(a)参数A(b)参数B(c)参数C图3 在步长h2=0.01的条件下各参数的相对误差与步长h1的关系
2)讨论了不同步长对参数的相对误差的影响, 并得出结论: 如果步长h1=h2=h, 则h越小, 其参数的相对误差越小; 如果步长h1≠h2, 则h1和h2需要满足一定关系才能得出较好的结果。 由此可知, 步长的选取与方程自身的特点密切相关。 如何根据方程自身特点选取有效的步长是需要继续探讨的问题。
3)文中的方法对于解为二次及低于二次的代数多项式并不适用,这是以后需要继续探索的问题。本文中以二阶常系数非齐次双曲型方程为研究对象,该方法也可以推广到常系数非齐次的抛物型和椭圆型方程的参数估计中。如果进一步讨论,还可以估算出偏微分方程的边界条件和初始条件,把这种方法推广到实际应用中。另外,本文中没有考虑变系数非齐次偏微分方程的估计方法,如何准确、有效地将该方法运用到变系数偏微分方程的参数估计中是需要深入研究的问题。
[1] 刘会超, 吴志健, 李焕哲, 等. 基于差分演化算法的双曲型方程参数识别[J]. 武汉大学学报(理学版),2015,61(2): 117-123.
[2] 熊盛武, 李元香, 康立山, 等. 用演化算法求解抛物型方程扩散系数的识别问题[J]. 计算机学报, 2000, 23(3): 261-265.
[3] 熊盛武, 李元香. 演化参数反演方法[J]. 武汉大学学报(理学版), 2001, 47(1): 37-41.
[4] STORN R, PRICE K. Differential evolution: a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359.
[5] RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Opposition-based differential evolution[J]. IEEE Transactions on Evolutionary Computation, 2008, 12(1): 64-79.
[6] 吴志健. 演化优化及其在微分方程反问题中的应用[D]. 武汉: 武汉大学, 2004.
[7] 彭亚绵, 杨爱民, 龚佃选, 等. 改进的最佳摄动量法及在反问题中的应用[J]. 数学的实践与认识, 2011, 41(5): 186-189.
[8] 彭亚绵. 双曲型方程参数识别反问题的解法[J]. 河北理工大学学报(自然科学版), 2007, 29(3): 105-109.
[9] 张世梅. 二维偏微分方程反问题的遗传算法研究[D]. 西安: 西安理工大学, 2005.
[10] 王小平, 曹立明. 遗传算法[M]. 西安: 西安交通大学出版社, 2002: 22-68.
[11] RUDIN L I, OSHER S, FATEMI E. Nonlinear total variation based noise removal algorithms[J]. Physica: D: Nonlinear Phenomena, 1992, 60(1/2/3/4): 259-268.
[12] 吴建成, 张大力, 刘家琦. 一维波动方程反问题求解的正则化方法[J]. 计算物理, 1995, 12(3): 415-420.
[13] 王松桂, 陈敏, 陈立萍. 线性统计模型线性回归与方差分析[M]. 北京: 高等教育出版社, 2014: 28-39.
[14] 谢鸿政, 杨枫林. 数学物理方程[M]. 北京: 科学出版社, 2008: 25-47.
[15] 李荣华, 刘播. 微分方程数值解法[M]. 北京: 高等教育出版社,2009: 67-76.

