基于AHP-FCM聚类的售电侧市场化改革进展评估

, , , , ,

(1. 国网浙江省电力公司, 浙江 杭州 310007; 2. 浙江华云信息科技有限公司， 浙江 杭州 310052; 3. 国网浙江省电力公司经济技术研究院, 浙江 杭州 310000; 4. 上海电机学院 电子信息学院, 上海 201306)

在新一轮电力体制改革中，售电侧的市场化改革是一个亮点，也是一个难点。开放售电侧市场可以让用户更加自主的选择售电主体， 从而促使电价下调， 但同时改革也会导致现有电力市场利益格局的改变， 给改革带来阻力。 为了稳步、 顺利推进售电侧的市场化改革， 有必要对售电侧的市场化改革进程开展相关理论研究。建立售电侧市场化改革的评价指标体系和进展评估模型，对售电侧市场化改革进行综合评估，有利于抓住售电侧市场化改革的重要核心，避免在改革的过程中走弯路[1-2]。

目前，针对售电侧市场化改革进展评估的研究较少，已有的评估指标体系不够全面，或缺少对评估模型的研究。文献[3]中分析了售电侧市场化改革的内涵以及改革带来的机遇与挑战，对售电侧市场化过渡期的问题尚未涉及。文献[4]中给出了售电侧市场化的制度设计和建议，指出了售电侧改革在电力体制改革中的定位，但也未考虑售电侧市场化改革进展的评估问题。文献[5]中对于售电市场放开情况下的售电策略和交易谈判进行了模型搭建及优化，但未涉及售电侧市场化改革评估模型的研究。基于以上讨论，结合目前售电侧市场化改革的实际，本文中提出一种基于层次分析(analytic hierarchy process, AHP)法和模糊C均值(fuzzyC-means, FCM)聚类算法的售电侧市场化改革进展评估模型[6-12]。首先，分析售电侧市场化改革的影响因素，建立全面的进展评估指标体系；其次，采用AHP对选取的指标进行分层，根据指标的重要程度和影响力等，设置一级、二级和三级指标，计算相应的评定权重，同时，对影响改革进程的关键指标进行权重优化；最后，基于FCM聚类算法，搭建售电侧市场化改革进展评估模型。

1 改革进程评估指标体系的建立

1.1 评估指标体系构建

建立客观、全面的评估指标体系，是搭建有效评估模型的前提和基础。评估指标体系应该能够真实、全面地反映各市场分区所处的改革阶段，既要考虑售电竞争主体，又要考虑电力用户。同时，指标体系还应该具备开放性和成长性，以适应评估对象的进一步发展。基于以上考虑，本文中主要从售电市场基础设施建设、售电市场机制建设、售电侧市场化进程、售电市场增值服务以及电力用户反馈5个方面搭建评估指标体系，并根据AHP法将以上5个方面作为二级指标进行分解，得到36个三级指标，如表1所示。

表中所示的三层次指标体系覆盖了与售电主体有关的各种因素，同时还引入了用户反馈指标，以确保评估结果更加的客观与真实。同时考虑到随着售电侧市场化程度的推进以及新能源技术的发展，本文中还将清洁能源接入率列入了指标体系， 用来衡量售电侧市场化改革的可持续发展程度。

1.2 评估指标的量化

1.2.1 量化评分标准

在售电侧改革进展指标体系中，36个三级指标具有不同的属性，量化时需要综合考虑。对于效益型指标(如指标1、3、4、6等)，量化值越大越好，可以对这类指标在[0，10]区间内打分；对于区间型指标(如指标16、 18、 21等)， 指标值越接近指定区间越好，可以用百分数来表示；而对于售电公司的被投诉率(指标35)这种逆向指标则要求越小越好，因此，综合以上原则，专家根据已有的电力市场化改革标准和相关规范，以及具有技术前瞻性的标准，通过分段赋值量化和专家打分制的等级评价方法对各指标评价打分，实现指标的量化[13-14]。具体量化等级评分标准如表2所示。

表2 售电侧市场化改革进展指标按等级分类评分标准

1.2.2 量化权重的设定

根据AHP理论，各个三级指标受二级指标影响， 且各指标间相对独立， 即， 假设各三级指标的决策变量为x1,x2, …,xn， 则二级指标的综合评判函数为

y=ω1x1+ω2x2+…+ωnxn，

(1)

在x1,x2,…,xn中，任取2个值xi,xj(i≠j)，比较它们对于评判函数y的贡献大小，然后按照表3所示的标度给xi/xj赋值。

表3 层次分析标度含义

根据表3得到三级指标决策变量两两比对后的数值，建立n阶矩阵A，则三级指标的量化权重值便可以通过以下迭代得到：

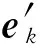
4)若数列{ek}是收敛的， 则记其极限为e， 且e=(a1,a2,…,an)；

5)得到权重系数ωi=ai,i=1,2,…,n。

根据以上步骤计算得到三级指标的权重系数ωi后，采用同样的步骤可以计算得到二级指标对总目标的排序权重，最终得到指标体系中各指标的权重值。

2 基于FCM聚类的进程评估模型

2.1 FCM聚类算法

在售电侧市场化改革进程的指标体系中，各指标之间相互独立，用来评估改革进程时需要进一步将大量的三级指标进行聚类，即先将改革划分为不同阶段，每一阶段再划分等级，最终提高评估的准确性[15]。根据以上分析，可以采用FCM聚类算法来搭建改革进程评估模型。

设待聚类的样本X={x1,x2,…,xn}属于P维欧式空间，xi∈P，i=1,2,…,n，将其分为C类；V={v1,v2,…,vC}为C个聚类中心点集；U=(uik)为隶属度矩阵，uik表示第k个样本在第i类中的隶属度，且满足定义目标函数为

(2)

式中：

其中m∈[1,∞)是加权指数，一般取1.5≤m≤2.5。

目标函数J(U,V)表示各类别中样本到其所在聚类中心的加权距离平方和，其中权重是样本xk对第i类隶属度的m次方。通过引入J(U,V)便可以将聚类问题转化为求minJ(U,V)的非线性规划问题，经优化迭代求解后，得出近似最优解U、V，便可以最终确定样本所属的类[16-21]。

具体的算法流程如下。

初始化： 给定聚类类别数C(数据个数)， 2≤C≤n， 取模糊加权指数m=2，设定迭代停止阈值ε，一般0.001≤ε≤0.01，初始化聚类原型模式V。

步骤1) 计算或更新划分矩阵U。

对于∀i,k，如果dik>0，则有

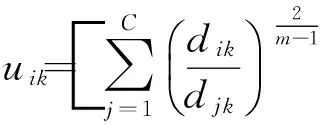
(3)

如果∃i,k，使dik=0，则有uik=1。

步骤2) 更新矩阵V。

(4)

步骤3) 计算目标函数J(U,V)，如果J(U,V)<ε，则算法停止并输出隶属度矩阵U和聚类原型矩阵V，否则重复步骤1)和步骤2)。

上述算法也可以先初始化聚类中心，然后再执行迭代过程，具体算法流程图如图1所示。

2.2 评估模型的搭建与仿真

将FCM算法用于售电侧改革过渡期进展评估一般可进行2次聚类，首先初始化聚类原型，对改革划分阶段，在充分研究我国电改历程与国外电改经验的基础上，根据我国当下售电市场改革的内在逻辑和改革方向，结合相关政策及改革试点情况，本文中将售电侧改革过渡期分为3个阶段，具体阶段划分见表4。

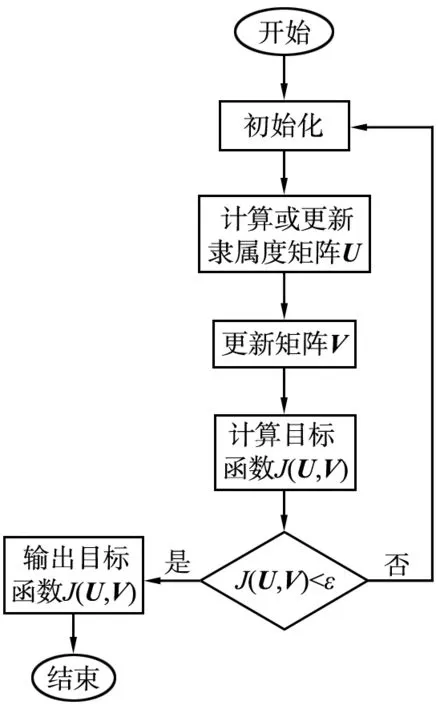
图1 模糊C均值聚类算法流程图

分析对象第一阶段第二阶段第三阶段市场核心 大用户直购电 以理货市场为核心的初级市场体系 不断完善的市场体系;不断丰富的市场主体用户群体 符合准入条件的大型工商业用户 用户逐步行使市场化自由选择权 绝大部分用户行使市场化自由选择权售电主体 电网企业或拥有发电背景的售电公司为主 独立售电公司逐步增多 多样化的售电主体交易内容 长期合同签订的电量合同 向电力交易过渡 多样化的交易品种

表中给出了市场核心、用户群体、售电主体以及交易内容4个方面在售电侧改革过渡期每一阶段的内涵，具体指出了改革过渡期衍化过程中，各阶段的典型特征。根据表4的阶段划分，可以在第1次聚类时确定n个市场(如以省为单位)的阶段所属，第2次聚类确定市场在具体某一阶段中的等级划分，评估模型如图2所示。

图2 基于模糊C均值算法的改革进度评估模型

图中以我国大陆31个省级行政区域为评估对象进行售电侧改革进展的评估，在第1次聚类时目标函数可取样本点数n=31(即待分类市场数)；C为预定的类别数目，因售电侧市场化改革分为3个阶段，故C=3；指标数为36，指标值由各省市实际数据并结合专家打分确定，用a1—a36共36组列向量来表示，并根据AHP理论计算各指标权重；选取模糊因子m=2。在进行第2次聚类时，n、C等参数值根据第1次聚类得到的具体结果与实际需求确定。

根据上述算法流程，用MATLAB软件仿真得到最终的聚类中心和隶属度值。将各市场分区对应的聚类中心进行比较，选择隶属度值最大的聚类中心作为该样本点所属的类别，最终确定分类结果。三聚类中心的二维仿真图如图3所示。由图可以看出，采用AHP和FCM算法可以有效地对各市场分区聚类，从而判断各市场分区所处的改革进程。

图3 三聚类中心的二维仿真图

3 算例分析

以浙江、山西、海南、四川、青海、广东、重庆等7个在经济基础、电力供需、电网发展、政策机制等方面存在差异的省市为例，取2016年和售电侧改革进一步发展的2020年为分析断面，根据该7个待评价市场分区的实际情况与相关数据，对改革进展进行评估。

3.1 2016年算例

2016年浙江、山西、海南、四川、青海、广东、重庆等7个待评价市场分区在售电市场基础设施建设、售电市场机制建设、售电侧市场化进程、售电市场增值服务以及电力用户反馈5个方面的36个指标，根据AHP理论计算得到各层指标的排序权重，如表5所示。

本轮售电侧改革自2015年启动以来已取得一定成果，但改革不是一蹴而就的， 从整体上看，各省市并未初步建立现货电力交易市场，即仍处于售电侧改革的第一阶段。在对该7个省市进行售电侧改革进展评估时，只进行1次聚类分析，确定其在售电侧改革第一阶段中的具体等级划分。仿真参数如下：样本点数n=7，指标数为36，类别数目C=3，选取加权指数m=2。

表5 售电侧市场化改革进展指标权重分配

根据算法流程和数据设定，仿真得到2016年市场分区的最终聚类中心和隶属度值，如表6所示。

根据表中的数据， 可以得到各市场分区所处改革进程的仿真结果。 仿真时用数字1—7依次代替上述7个省份， 可以看出属于第一等级的市场分区是广东和重庆，第二等级的是浙江和四川，第三等级的是山西、海南和青海。

表6 2016年各市场分区隶属度值

用数字1—7依次代替上述7个省份，根据表6中的数据，可以看到各市场分区所处的改革进程，属于第一等级的市场分区是广东和重庆，第二等级的是浙江和四川，第三等级的是山西、海南和青海。

总体而言，所选7个省市在2016年均处于售电侧市场化改革第一阶段(大用户直购阶段)，但改革发展的快慢有所差别，各省在第一阶段中所处等级不同，按照等级由高到低划分，大致顺序为广东、重庆、浙江、四川、山西、海南、青海，该分析结果与实际电力市场情况基本吻合。

3.2 2020年算例

到2020年，经过一段时间的售电侧市场化改革， 因各省市基础不一，发展快慢有别，很可能将呈现不同的改革阶段(如有的省份可能已步入成熟现货市场，有的省份还可能处于大客户直购阶段)，故首先需要通过聚类分析确定其阶段所属，再进行第2次聚类以确定其在售电侧改革某一阶段中的具体等级划分。仿真参数仍取样本点数n=7，指标数为36，类别数目C=3，模糊因子m=2。

同2016年算例，仿真得到2020年市场分区的最终聚类中心和隶属度值，如表7所示。

表7 2020年各市场分区隶属度值

类似2016年，通过表7可以看出2020年属于第一类市场分区的省份有浙江、广东和重庆，属于第二类市场分区的省份为山西和四川，属于第三类市场分区的是海南和青海。预计在2020年，广东、浙江、重庆已步入售电侧改革第三阶段，即成熟现货市场；四川、山西处于售电侧改革第二阶段，即初级现货市场；海南、青海可能仍处于售电侧改革第一阶段，即大用户直购市场。另外，由于仿真只取了7个省份作为样本，因此，在第1次聚类后，各阶段的样本数量过少，对模糊聚类分析的精确度有较大影响，故不再进行第2次聚类来确定其在售电侧改革某一阶段中的具体等级划分。

4 结语

针对售电侧市场化改革过渡期呈现出的不同特征以及出现的问题，本文中构建了改革进展评估指标体系，并采用AHP理论对各指标进行权重量化，对量化后评估指标进行FCM聚类，搭建售电侧市场化改革进展评估模型。该评估模型降低了FCM对初值的敏感度，避免陷入局部最优，可以全面、客观的评定改革所处的进程，对于小样本聚类依然具有较好的准确性。仿真结果以及算例分析表明，通过将AHP与FCM聚类算法相结合，可以更加客观、真实地对各市场分区所处的阶段和等级进行评估，仿真结果与各市场分区的实际情况基本吻合。本研究成果无论是对政府职能部门，还是对电网企业和电力用户来说，均具有较高的应用和参考价值，对于保证改革的稳步有序推进具有一定的现实意义。

[1] 国务院. 国务院关于印发电力体制改革方案的通知(国发[2002]5号)[Z/OL].[2017-01-13]. http://www.lawxp.com/statute/s1068870.html.

[2] 王金雪, 韩静轩, 王金亮. 山东省电力消费和经济发展关系的协整分析[J]. 济南大学学报(自然科学版), 2008, 22(4): 21-24.

[3] 国务院. 关于进一步深化电力体制改革的若干意见(中发[2015]9号)文[Z/OL].[2017-01-13]. http://www.ne21.com/news/show64828.html.

[4] 朱刚. 售电侧改革的探索与思考[J]. 中国电业, 2016(11): 22-23.

[5] 白杨, 谢乐, 夏清,等. 中国推进售电侧市场化的制度设计与建议[J]. 电力系统自动化, 2015, 39(14): 1-7.

[6] 李欢欢, 张晨, 吴静,等. 售电放开政策下发电商售电策略与交易谈判优化模型[J]. 电力建设, 2017，38(3): 123-129.

[7] Public Utility Commission of Texas. Report to the 84th Texas legislature: scope of competition in electric markets in Texas[R/OL].[2017-01-13]. http://www.puc.texas.gov/industry/electric/reports/scope/2015/2015scope_elec.pdf.

[8] 杨小彬, 李和明, 尹忠东,等. 基于层次分析法的配电网能效指标体系[J]. 电力系统自动化, 2013, 37(21): 146-150.

[9] 乔伟峰, 曾洪云, 李云梅. 基于层次分析法的滇中经济区土地资源集约利用研究[J]. 南京师范大学学报(自然科学版), 2013, 36(2): 113-118.

[10] ZHONG H, XIE L, XIA Q. Coupon incentive-based demand response: theory and case study[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1266-1276.

[11] 王永欣, 张化祥, 王爽. 基于属性加权的主成分分析算法[J]. 济南大学学报(自然科学版), 2015, 29(6): 438-443.

[12] 李强, 周京阳, 于尔铿,等. 基于混合量测的电力系统状态估计混合算法[J]. 电力系统自动化, 2005, 29(19): 31-35.

[13] 郑鑫, 张韧志. 一种基于模糊C均值聚类的协同过滤推荐算法[J]. 济南大学学报(自然科学版), 2016, 30(1)：55-59.

[14] ZADEH L A. Fuzzy sets[J]. Information and Control， 1965, 8(3): 338-353.

[15] BEILMAN R, KALABA R, ZADEH L A. Abstraction and pattern classification[J]. Journal of Mathematical Analysis and Applications, 1966, 13(2): 1-7.

[16] RUSPINI E H. A new approach to clustering[J]. Information and Control, 1969, 15(8): 22-32.

[17] DUNN J C. A graph theoretic analysis of pattern classification via Tamura’s fuzzy relation[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1974, 4(3): 310-313.

[18] BEZDEK J C. A convergence theorem for the fuzzy ISODATA clustering algorithm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1980, 2(1):1-8.

[19] WAGSTAFF K, CARDIE C, ROGERS S, et al. Constrained K-means clustering with background knowledge[C]//Proceedings of the Eighteenth International Conference on Machine Learning. San Francisco: Morgan Kaufmann Publishers Inc., 2001: 577-584.

[20] 庄瑞格,倪泽邦,刘学艺.基于拟蒙特卡洛的K均值聚类中心初始化方法[J].济南大学学报(自然科学版),2017,31(1): 36-41.

[21] 林济铿，刘露，张闻博,等. 基于随机模糊聚类的负荷建模与参数辨识[J]. 电力系统自动化, 2013, 37(14): 50-58.