高强度混凝土高温爆裂时的格里菲思准则
, , , ,
(1. 北方民族大学 a. 化学与化学工程学院; b. 数学与信息科学学院, 宁夏 银川 750021;2. 宁夏旭日众粒环保科技有限公司, 宁夏 银川 750200)
高强度混凝土或岩石等脆性材料在适宜的含水率时具有高温爆裂倾向,主要原因是在极端高温环境下,其孔隙或裂隙中的水从液相变为气相。这些孔隙大多与外界不贯通, 导致高压蒸汽不能及时排出,蒸汽压力使得混凝土受到由里向外的膨胀力,这种应力状态等效于三向受拉;另外,极端高温不仅引起混凝土结构的退化,还产生了不可忽视的温度应力,最终引起了混凝土的剥落与爆裂[1-3]。国外学者针对这个问题从多场耦合角度进行了研究[4-6],也有学者考虑温度梯度,测量了孔隙蒸汽压力,并给出评价退化的量化指标[7-8]。
混凝土或岩石等非均质脆性材料的破坏机理是一个传统的复杂问题[9-10]。 鉴于材料自身物理属性的差异, 一个准则很难解释所有破坏机制, 因此先后出现了多个破坏准则, 代表性的有最大正应力理论、 最大正应变理论、 最大剪应力理论、 八面体剪应力理论、 莫尔-库仑准则、 格里菲思理论, 以及其他一些经验准则, 如霍克-布朗准则等。 这些准则都能解释实际工程中的一部分问题, 但是不能解释所有的破裂机制[11-14]。 高强度混凝土在极端高温下产生的蒸汽压力对微裂隙腔体边缘产生劈裂效应, 抑制了外力作用下内部微裂隙的闭合, 而蒸汽压力的存在又减小了有效应力。 针对这些特征, 本文中将有效应力原理下的格里菲思准则应用到高强度混凝土高温爆裂的研究中, 探讨不同应力状态下考虑有效应力时的破裂形态, 以及特殊主应力比下的几种典型破裂模式。
1 格里菲思理论及其普遍意义
格里菲思理论认为材料内部存在许多细微裂隙,这些裂隙边缘在力的作用下会产生应力集中,裂缝在边缘处继续扩展,最终导致材料完全破坏。格里菲思准则力学模型建立的思想[15]主要包括:假设介质中包含大量微裂隙或微孔洞,其分布特征如图1所示,其中σ1、σ3分别为第一、三主应力;β为长轴方向与第一主应力σ1之间的夹角;x轴取裂隙走向;y轴垂直于裂隙走向;σx、σy分别为x、y轴方向的正应力,τxy为平行于x轴方向的剪应力。格里菲思准则在模型抽象时假定条件较多,主要包括不考虑摩擦对压缩下闭合裂缝的影响,并假定椭圆形裂缝的扩展从最大拉应力集中点开始,而对于极端高温环境下的高强度混凝土,较大的蒸汽压力使内部裂隙有膨胀和劈裂扩展的趋势,这一特征与格里菲思准则的假定较为一致。
格里菲思理论对应的强度准则[15]如下。
1)当σ1+3σ3>0时,有
(σ1-σ3)2-8Rt(σ1+σ3)=0,
(1)

σ1、σ3—第一、三主应力;β—长轴方向与第一主应力σ1之间的夹角;x轴—裂隙走向;y轴—垂直于裂隙走向;σx、σy—x、y轴方向的正应力,τxy—平行于x轴方向的剪应力。图1 混凝土中的微裂隙受力示意图
式中Rt为混凝土的抗拉强度。此时最危险的破裂角为
(2)
2)当σ1+3σ3<0时,有
σ3+Rt=0。
(3)
此时最危险的破裂角为
β=0。
(4)
由于格里菲思理论考虑了材料的内部缺陷,即包含大量微裂隙或微孔洞,因此,由格里菲思理论得出的结果与试验测定的结果高度一致[16-20]。
2 有效应力原理下高温爆裂时的格里菲思准则
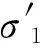
1)当σ1+3σ3>4p时,2个主应力的力学效应以压缩为主,主应力抑制了蒸汽压力对裂缝的破裂效应,因此有
(σ1-σ3)2-8Rt(σ1+σ3-2p)=0。
(5)
此时最危险破裂角不仅与2个主应力的比例有关,还与蒸汽压力p有关,β需要修正为
(6)
2)当σ1+3σ3<4p时,2个主应力的力学效应以拉伸为主,主应力加剧了蒸汽压力对裂缝的破裂效应,因此有

(7)
此时最危险破裂角没有变化,仍然为β=0。
3 高压蒸汽压力下的破坏形态
3.1 当σ1+3σ3>4p(β≠0)
对于不等式σ1+3σ3>4p,由于岩石力学规定压为正、拉为负,且σ1≥σ3,因此不等式成立的条件有2种可能。
1)压-压组合,即σ1>0,σ3>0,且σ1+3σ3>4p。由于不等式σ1≥σ3恒成立,因此这2个主应力之间的关系有2种特殊情况:①σ1/σ3接近于1,即2个方向压应力相当,无明显主压应力;②σ1/σ3远大于1,即2个方向压应力相差悬殊,为主压应力。
2)拉-压组合,即σ1>0,σ3<0,且σ1-|3σ3|>4p。同样,σ1≥σ3恒成立,因此这2个主应力之间的关系也有2种特殊情况:①σ1/|σ3|接近于1,且σ1-|3σ3|>4p,无明显主压应力或主拉应力;②σ1/|σ3|远大于1,且σ1-|3σ3|>4p,σ1为主压应力。
满足不等式σ1+3σ3>4p的应力组合有压-压组合和拉-压组合2种情况,而每种组合下,主应力比又有2种特殊情况,不同情况下的破裂形态对比如表1所示。

表1 当σ1+3σ3>4p时,2种特殊主应力比下的控制应力与破裂特征
3.2 当σ1+σ3<4p(β=0)
对于不等式σ1+3σ3<4p,由于岩石力学规定压为正、拉为负,且σ1≥σ3,因此不等式成立的条件有2种情况。
1)拉-拉组合,即σ1<0,σ3<0,且|σ1|+|σ1|+3|σ3|>4p。由于σ1≥σ3恒成立,因此这2个主应力之间的关系有2种特殊情况:①|σ3|/|σ1|接近于1,即2个方向拉应力相当,无明显主拉应力;②|σ3|/|σ1|远大于1,即2个方向拉应力相差较大,σ3为主拉应力。
2)拉-压组合,即σ1>0,σ3<0,并且σ1+3|σ3|>4p, 此时2个主应力之间的关系有2种特殊情况: ①|σ3|/σ1接近于1,无明显主拉应力和主压应力;②|σ3|/σ1远大于1,σ3为主拉应力。
同样,满足不等式σ1+3σ3<4p的应力组合有拉-拉组合和拉-压组合2种情况,而每种组合下,主应力比又有2种特殊情况,不同情况下的破裂形态对比如表2所示。

表2 当σ1+3σ3<4p时,2种特殊主应力比下的控制应力与破裂特征
3.3 特殊应力比下破裂形态的进一步阐述
3.3.1 拉断
拉应力主导下的拉断破坏模式见图2。 由图可知, 在多轴受拉或拉-压应力状态下, 主拉应力σ3在岩石或混凝土中起主要控制作用, 当主拉应变大于极限拉应变时, 先在最薄弱的截面形成近似垂直于σ3方向的裂缝, 然后逐渐展开。 随着破裂面的增大, 有效受拉面的面积减小。 最终, 试件突然被拉断成两半, 与棱柱体单轴受拉破坏过程和特征完全相同。

图2 拉应力σ3主导下的拉断破坏
试件断裂面一般与最大主拉应力σ1方向垂直,近似于一个平面。当σ1和σ3均为拉应力且σ1/σ3为1.0~2.0时,断裂面可能与σ1轴成一个夹角,这取决于脆性材料抗拉强度的随机分布。
3.3.2 柱状压坏
图3所示为三向不均衡受压时的柱状破坏。由图可知,在多轴受压或拉-压应力状态下,当主压应力σ1远大于主应力σ3时,沿2个垂直方向会产生拉应变。当该拉应变大于其极限值后,形成平行于σ1也平行于试件侧表面的2组裂缝面。裂缝面逐渐扩展乃至贯通全试件,最终将柱体分离成短柱群而破坏。
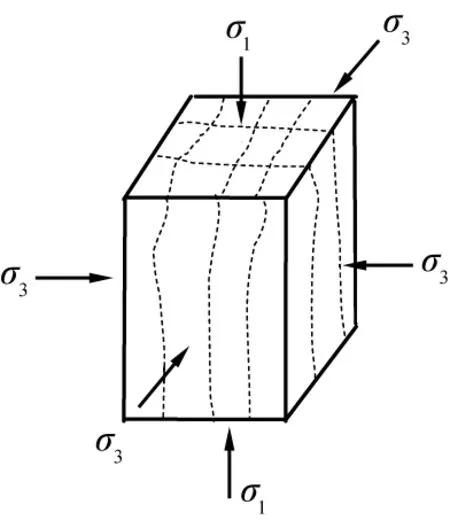
σ1、σ3—第一、三主应力。图3 三向不均衡受压时的柱状破坏
3.3.3 斜剪破坏
图4所示为三向不均衡受压时的斜剪破坏。由图可知,三轴受压时若σ1与σ3的差值较大,则剪应力(σ1-σ2)/2较大,破坏将发生在某一斜截面上,方向与σ1轴有一个夹角,破裂面上产生剪切错动和碾压的痕迹。

σ1、σ3—第一、三主应力。图4 三向不均衡受压时的斜剪破坏
3.3.4 挤压流动
图5所示为三向均衡受压时的挤压变形和破坏特征。由图可知,此时三轴受压且σ1和σ3大小相当,3个方向的主应变均为压缩,此时脆性材料也表现出一定的延性特征。在火灾等极端高温环境下,混凝土的强度会发生显著退化,还有不可忽略的温度应力,还可能存在较大的蒸汽压力,导致塑性变形的进程加快。

σ1、σ3—第一、三主应力。图5 三向均衡受压时的挤压变形和破坏特征
4 蒸汽压力对破裂角及其破裂机理的影响
4.1 蒸汽压力对破裂角的影响
考虑蒸汽压力, 并且在格里菲思准则中引入有效应力原理后, 不同应力状态下的破裂角β如表3所示。

表3 引入蒸汽压力前、后格里菲思准则中破裂角的变化
由表可知,有效应力下的格里菲思准则中,满足σ1+3σ3>0或σ1+3σ3>4p条件的主应力σ1和σ3有多种组合,最危险破裂角也会发生改变,分别讨论如下:
1)当σ1+3σ3>0或σ1+3σ3>4p时。
①压-压组合, 即σ1>0,σ3>0, 显然有σ1+3σ3>0, 而与破坏时的主应力之和(σ1+σ3)相比,蒸汽压力p与之相差至少1个数量级,因此一般情况下σ1+σ3-2p>0总是成立的。
②拉-压组合,即σ1>0,σ3<0,且σ1+3σ3>0,则σ1+σ3>σ1+3σ3>0,同样,与破坏时的主应力之和(σ1+σ3)相比,蒸汽压力p与之相差至少1个数量级,因此一般情况下σ1+σ3-2p>0也总是成立的。
综合压-压组合与拉-压组合,由于σ1-σ3≥0成立,且一般情况下σ1+σ3-2p≥0成立,因此有
(8)
由于β为锐角,因此有

(9)
由此可知,引入蒸汽压力后最危险破裂角变小,且蒸汽压力越大,破裂角减小幅度越大。

4.2 蒸汽压力对破裂机理的影响
图6所示为破裂角的变化与破坏模式的转换。由图可知,蒸汽压力使得破裂角β变小,与之对应的破裂面方位角α增大,且蒸汽压力p越大,该方位角α变化幅度越大。破裂面的改变是破坏机理转换的宏观体现,即随着破裂面陡峭程度的增加,压剪破坏的趋势减弱,拉剪破坏的趋势增强,与之对应的破坏模式从剪切向张拉转变,而格里菲思理论更适合于拉剪破坏。由此可知,高强度混凝土在高温爆裂时的强度特征用格里菲思准则来描述是可行的。
从这个意义上说,格里菲思准则与莫尔-库仑准则并不是2个截然不同的强度准则,也有辩证统一的一面,即格里菲思准则侧重于描述拉剪破坏,而莫尔-库仑准则更适合于描述压剪破坏。最终的破裂角只是不同应力状态下不同破坏机制的宏观体现。
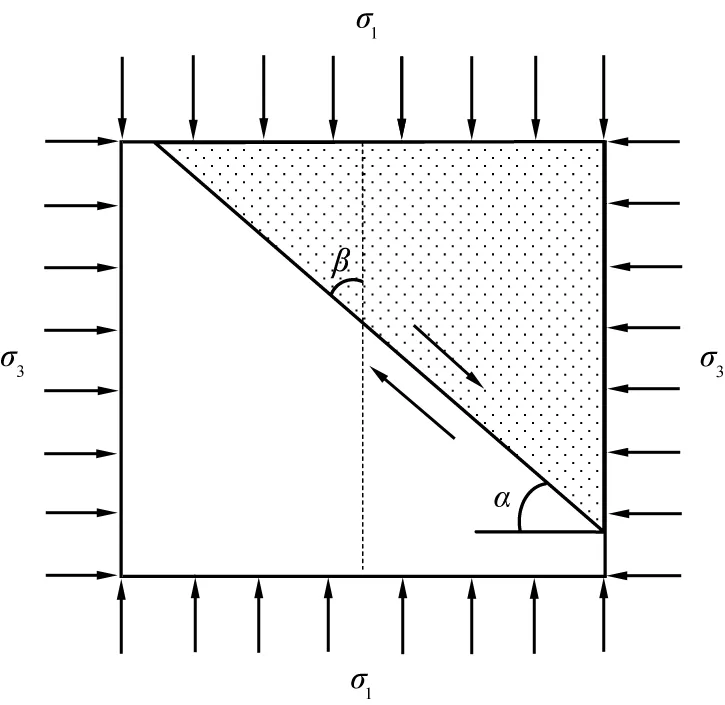
σ1、σ3—第一、三主应力;α—破裂面方位角。图6 破裂角的变化与破坏模式的转换
4.3 高温时和高温后强度的差异
目前,极端高温后岩石或混凝土的强度实验研究比较丰富,但是关于高温过程中的强度实验较为缺乏,而这2种情况是截然不同的2个问题。高温后的强度问题是一个强度退化问题,而高温下的强度问题是温度应力、高温蒸汽压力和外力3个物理场共同耦合下的问题。由此可知,要揭示高温爆裂机理,除了研究脆性材料的细观特征外,还必须开展高温下的强度研究,目前这方面的试验研究开展的较少,主要是试验环境对硬件的要求较高,让试件处于极端高温下再进行强度实验,包括单轴以及三轴等实验,这给试样的固定和加载以及数据的测量都带来了困难,这方面的研究今后需要加强。
5 结论
基于有效应力原理, 利用格里菲思准则分析高强度混凝土在极端高温下的破裂问题, 得出如下结论:
1)高强度混凝土高温爆裂时蒸汽压力在裂纹边缘产生应力集中,引起裂缝的扩展直至贯通,这一特征与格里菲思准则的物理力学模型较为接近,用格里菲思准则是可行的;
2)基于有效应力原理,将极端高温时高强度混凝土内部产生的蒸汽压力引入格里菲思准则中,扩大了格里菲思准则的应用范围,也是对格里菲思准则的修正;
3)蒸汽压力改变了破裂角,破裂机制也从压剪破坏向拉剪破坏过渡,对于抗压强度远大于抗剪强度的脆性材料,最终的强度也随之减小,这也是蒸汽压力对强度影响的机理所在;
4)蒸汽压力减小了高强度混凝土中的有效应力,高温还产生了不可忽略的温度应力,因此, 混凝土的高温爆裂是一个复杂的多场耦合问题,有必要从多个维度开展理论分析和试验研究。
[1] 鞠杨,刘红彬,田开培,等. RPC高温爆裂的微细观孔隙结构与蒸汽压变化机制的研究[J]. 中国科学: E辑,2013,43(2):141-152.
[2] 郭荣鑫,何科成,马倩敏,等. 改性轻骨料混凝土高温抗压性能及微观结构[J]. 建筑材料学报, 2017,20(3): 333-338,344.
[3] 柳献,袁勇,叶光,等. 高性能混凝土高温爆裂的机理探讨[J]. 土木工程学报,2008,41(6): 61-68.
[4] 唐世斌,唐春安,李连崇,等. 脆性材料热-力耦合模型及热破裂数值分析方法[J]. 计算力学学报,2009,26(2): 172-179.
[5] KANÉMA M, PLIYA P, NOUMOWÉ A, et al. Spalling, thermal, and hydrous behavior of ordinary and high-strength concrete subjected to elevated temperature[J]. Journal of Materials in Civil Engineering, 2011,23(7): 921-930.
[6] GUERRIERI M, FRAGOMENI S. Mechanisms of spalling of concrete panels of different geometry in hydrocarbon fire[J]. Journal of Materials in Civil Engineering, 2016,28(12): 04016164.
[7] FARES H, TOUTANJI H, PIERCE K, et al. Lightweight self-consolidating concrete exposed to elevated temperatures[J]. Journal of Materials in Civil Engineering, 2015,27(12): 04015039.
[8] TERRAS G P, BISBY L, BARBEZAT M, et al. Fire behavior of thin CFRP pretensioned high-strength concrete slabs[J].Journal of Composites for Construction, 2012, 16(4): 381-394.
[9] 邵兵,王向东,王跃锋,等. 混凝土压缩损伤参数的尺寸效应分析[J]. 济南大学学报(自然科学版), 2012, 26(3): 315-318.
[10] 于静巍,王向东,朱小婷,等. 混凝土结构裂缝的动力稳定性损伤与断裂[J]. 济南大学学报(自然科学版), 2017, 31(3): 244-249.
[11] 刘红彬. 活性粉末混凝土的高温力学性能与爆裂试验研究[D]. 北京: 中国矿业大学(北京),2012.
[12] 石东升,王海波,刘曙光. 影响火灾下混凝土爆裂因素的试验研究[J]. 内蒙古工业大学学报(自然科学版),2007, 26(2): 129-135.
[13] 吴波,袁杰,李惠,等. 高温下高强混凝土的爆裂规律与柱截面温度场计算[J]. 自然灾害学报,2002,11(2): 65-69.
[14] 李荣涛,李锡夔. 混凝土中化学-热-湿-力耦合过程的数值方法[J]. 力学学报,2006,38(4): 471-479.
[15] 徐志英. 岩石力学[M]. 北京: 中国水利水电出版社,1993.
[16] 王里,刘红彬,鞠杨,等.高强高性能混凝土高温爆裂机理研究进展[J]. 力学与实践,2014,36(4):403-412.
[17] 昝月稳,俞茂宏,王思敬. 岩石非线性统一强度准则[J].岩石力学与工程学报,2002,21(10): 1435-1441.
[18] 俞茂宏. 双剪强度理论及其应用[M]. 北京: 科学出版社,1998.
[19] 郭少华, 周绍青, 邹春伟.压缩荷载条件下岩石类材料的断裂模式研究[J]. 实验力学, 2008, 23(2): 149-156.
[20] 宋建波,张卓元,于远忠. 岩体经验强度准则及其在地质工程中的应用[M]. 北京: 地质出版社,2002.

