浅谈如何实施“三象一作”的教学模式

江苏灌云县下车中心小学（222231） 刘 建

在“小数的意义”的教学中，笔者尝试实施“三象一作”的教学模式，启发、鼓励学生关注数学现象，在绘制图像的过程中，逐步完成知识建构。

一、创设情境，积累数学活动经验

教学“小数的意义”时，首先要根据小数的特点和学生的认知基础列举有趣的数学现象。在学生初步认识小数的重要性后，教师不妨设计测量小宝宝身高的体验式情境。首先，测量三个月大的小宝宝的身高（图略）。学生观察后发现测量结果无法用整数表示，教师便可趁机诱导学生尝试转化思维方式，从计量单位的角度去考虑：将1米平均分为10等份，一份即是1分米。在教师的启发下，学生有了新进展：“经测量，小宝宝的身高是6分米，如果以米为单位，则为米，也就是0.6米。”这样，就顺利揭示了一位小数的现实意义。

当小宝宝六个月大时，再次测量身高，发现小宝宝的身高介于6分米和7分米之间，若以分米为单位很难得出准确的数据。由于有了上一次的操作经验，学生想到进一步划分分米，得出更精细的长度单位——厘米，这时两位小数便自然而然地产生了。继续划分，就能得出三位小数、四位小数。

在这样环环相扣的生活情境中，一位小数、两位小数、三位小数的出现顺理成章，毫无违和感和疏离感。经过一连串的探索活动，学生的脑海中积累了大量关于小数的材料，为绘制心智图像奠定了基础。

二、激活心智图像，丰富内涵

心智图像是一种直觉印象，具有概括性和抽象性。小数是一个较为抽象的数学概念，为了较为真实地绘制关于小数的心智图像，教师应做到以下两点。

第一，用米尺作为测量教具。学生借助刻度尺认识了各种长度单位，并认清了它们之间的进率关系。因此在教学小数意义时，教师把1米等分成若干份，分别获取1米的十分之一、百分之一、千分之一，并表示成不同位数的小数。此时，勾勒出学生的心智图像轮廓为：1米，若等分成10份，每份为1分米，占1米的写成小数是0.1米；若等分成100份，每份则是1厘米，占1米的写成小数是0.01米；若分成1000份，每份则是1毫米，占1米的用小数表示是0.001米。这样一来就能和 0.1、0.01、0.001搭上线、对上号，形成了从整数到分数，再跃升到小数的心智图像。

第二，用一个正方体代表单位“1”。形成的心智图像如下：把正方体平均切成10份后，每份占正方体的用小数0.1表示；平均切成100份，每份占正方体的用小数0.01表示；平均切成1000份，每份占正方体的，用小数0.001表示。

三、深度抽象，认识本质

人脑具有抽象智能，通过对现象的积累、组合、联系，逐步形成概念。因此，教师要指导学生归纳，完成深度抽象。

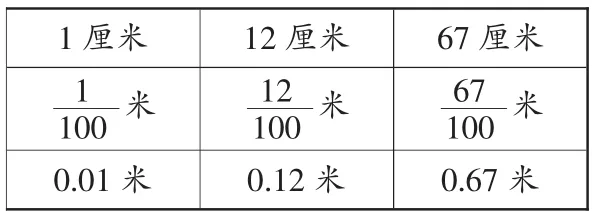
第一，正向感受小数的意义。在学生建立整数、分数与小数之间的纵向联系后（如下表），教师要及时指导学生进行横向比较：第一行是整数，以厘米作为单位；第二行是分数，以米作为单位，表示不够整数米；第三行是小数，也以米作为单位，表示不够整米数。接着，教师以问题：“为什么以厘米作单位的数改写为以米作单位的数时，用分数表示要以100作分母？用小数表示要用两位小数？”启发学生正向思考。

第二，逆向理解小数的意义。创设这样一个环节：请你选择恰当的几何模型来表示 0.001、0.008、0.01、0.04、0.12、0.67、0.7 等数。

通过对比甄选，学生会发现表示0.1、0.4、0.7选用①号模型，0.01、0.04、0.12、0.67②号模型，其余小数选用③号模型。利用数形结合中进行归类，形象且直观，学生能清晰地认识到小数的意义。

综上所述，运用“三象一作”的理论指导小数意义教学实践，从数学现象入手，通过三个层级的抽象概括，学生对小数的理解就会逐渐明朗清晰。