热轧板带凸度影响因素的敏感性分析
梁冰,何飞,杨德斌,杨荃,刘朋
热轧板带凸度影响因素的敏感性分析
梁冰1, 2,何飞1, 3,杨德斌2,杨荃3,刘朋4
(1. 北京科技大学 钢铁共性技术协同创新中心,北京,100083;2. 北京科技大学 机械工程学院,北京,100083;3. 北京科技大学 国家板带生产先进装备工程技术研究中心,北京,100083;4. 首钢技术研究院,北京,100043)
基于支持向量机方法,针对热轧工艺生产过程中的板带凸度进行影响因素敏感性分析。采用支持向量机建立工艺参数与板带凸度的关系模型,引入Morris及Variance-based敏感性分析方法,获得影响板带凸度的关键因素。研究结果表明:基于支持向量机建模的Morris及Variance-based敏感性分析方法可以准确定位关键因素,为实现热轧过程中的生产控制提供指导。
板带凸度;敏感性分析;Morris;Variance-based
板带凸度是描述板带横截面形状的主要指标之一,一方面反映了板带在生产过程中的横向板厚差,另一方面直接影响板带的板形状态和辊形调控目标,对生产过程的稳定和产品质量的控制有决定性作 用[1−2]。对于轧制生产过程,孔繁甫等[3−4]利用力能关系等物理分析方法,建立了一些轧制过程机理模型,并控制辊形及板形。然而,随着人们对热轧板带性能越来越高的要求,改进轧制控制模型以提高控制精度的要求也越来越迫切。随着传感技术、控制技术和数据库技术的发展,现代化生产企业产生了大量实际生产数据,并利用数据分析手段来获取生产经验,改变传统的人工经验认识生产过程的方法。为了更好地认识轧制过程中控制变量、测量变量等因素对板带性能的影响,本文作者在建立有效的生产过程数据分析模型的基础上,将敏感性分析引入生产过程分析,研究工艺参数变量发生某种变化时对板带凸度的影响程度,并将工艺参数变量按重要性排序,为实现热轧过程的生产控制提供参考。
1 影响热轧板带凸度的因素
板带的凸度是由负载辊缝形状决定的,一切影响负载辊缝形状的因素都会影响板形。这些影响因素可归结为内因(金属本性)和外因(轧制条件) 2个方面。金属本身的物理性能(如硬化特性、变形抗力)直接影响轧制力,因而与板带凸度密切相关。金属的几何特性特别是板带的宽厚比、入口板带凸度是影响板带凸度的另一个重要因素;轧制条件的影响更为复杂,轧辊的凸度直接构成了初始辊缝形状,而轧制压力分布在轧制过程中的变化会对辊系变形和辊缝产生重大影响[5]。本文主要介绍以下几个影响因素。
1) 板宽对板带凸度的影响。目前,热轧板带向大宽厚比的方向发展,所以有必要考虑板宽对板形的影响。随着板带宽厚比的增大,金属在轧制过程中横向流动变得困难,从而直接影响轧制压力和张力分布,对板带凸度产生较大影响。
2) 工作辊凸度对板带凸度的影响。在热轧过程中,轧辊凸度一般由轧辊初始凸度、热凸度和磨损凸度组成。而工作辊由于直接与板带接触,其凸度会对板带凸度产生直接影响。工作辊凸度变大,表明板带中部的压下量增大,会直接导致板带中部厚度减小而使板带凸度减小。
3) 弯辊力对板带凸度的影响。弯辊力控制是热轧过程中控制板带凸度的最常用手段,弯辊力控制是否恰当直接影响板形质量。目前,在热轧生产中一般采用正弯辊,即若弯辊力增大,则工作辊两边抬起而中部下压,这样会使板带中部压下量增大导致板带凸度减小。
由于影响板带凸度的因素存在多变量、强耦合、非线性以及时变性等特点,若希望在众多因素中寻找影响板带凸度的关键变量,采用传统方法很难找到。因此,本文作者为进一步提高轧制控制模型的控制精度,将敏感性分析的方法引入热轧板带凸度数据的建模,进而分析得出变量的敏感性排序来认识生产过程[6−7]。
2 基于模型的敏感性分析方法
敏感性分析用于分析数学模型或系统中不同来源输入的差异对输出结果的影响,可以测试输入存在波动时模型或系统的鲁棒性,增强模型或系统中对输入输出相互关联、影响程度的解释[8−9]。
敏感性分析思路及方法的运算流程大致如下:
1) 量化输入的差异性,给出分布范围或概率密度函数[10];
2) 确定待分析模型,并保证该模型能较为准确地描述输入变量和输出变量之间的关系;
3) 根据选用的敏感性分析方法,运行模型得到输入变量差异变化时的输出结果[11];
4) 根据得出的模型输出结果,计算各工艺参数对输出结果的敏感性或重要程度。
2.1 Morris全局敏感性分析方法
Morris全局敏感性分析方法是通过在输入变量值域内对样本进行一系列的局部调整而得到的[12−15]。
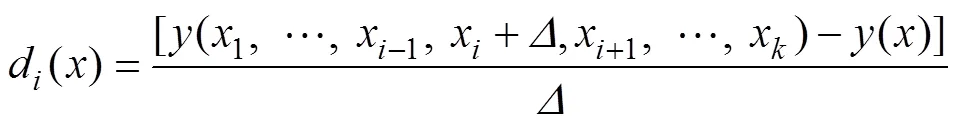

Morris全局敏感性分析中,以有限分布F的绝对均值和标准差来表征变量敏感性;表征变量的敏感性,可用于变量重要程度排序;表征变量与其他变量协同作用的敏感性。敏感性越大,表示对输出变量的作用越明显。具体计算公式如下:


式中:i为变量的基效应;为实验重复次数,一般取=3,确保在随机抽样中,不遗漏样本。
计算步骤如下:
1) 在数据空间中随机抽取1个样本作为起始点,第1次运行训练模型,计算其输出结果;
2) 变化该样本中变量的取值,变化量为,第2次运行训练模型,计算其输出结果;
3) 由步骤1)与步骤2)的输出结果,计算变量的基效应d();
4) 继续变化该样本点其他变量中的1个,并计算其输出结果,直至所有输入变量均发生变化;
5) 重复步骤1)~4),每次均从不同的起始点出发,共重复次;
6) 计算*和,作为衡量变量敏感性的评价指标。
2.2 Variance-based敏感性分析方法
Variance-based敏感性分析方法是一种全局敏感性分析法[16−18]。
2.2.1 方差的分解
将由输入、输出变量训练得到的模型视为过程函数=(),其中=(1,2,…,X),将的变异信息分解[13],得到X单独作用的部分V及X与X同时作用的部分V,以此类推,则有
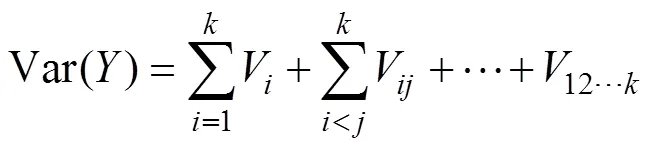
2.2.2 一阶效应(First-order indices)
定义敏感性指标的一阶效应S,代表变量X的变化对输出变量变化的贡献率[19]

除一阶效应外,还有二阶、三阶及更高阶的效应。二阶效应S代表变量X与X交互作用对输出变量变化的贡献率;三阶效应S代表变量X,X与X交互作用对输出变量变化的贡献率,以此类推,则有
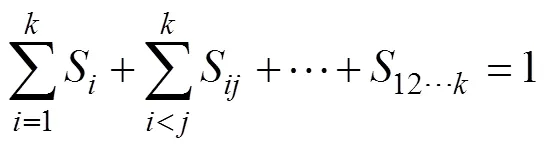
2.2.3 总效应(Total-effect index)
总效应Ti代表由变量X变化所引起的一阶效应及与其他变量交互作用引起的所有高阶效应的总和[20−21]。

并且

2.2.4 计算步骤[14]

根据以下给出的估计量,计算敏感性:
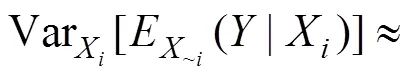


3 实验与结果分析
本文利用仿真数据验证方法的有效性,同时利用支持向量机(Support Vector Machine, SVM)建立板带凸度数据的质量模型,并进行Morris和Variance-based敏感性分析,获得影响板带凸度的关键工艺参数。
3.1 仿真实验
仿真数据采用仿真模型=1−22+53+13+23(其中,=(1,2,3);X=−5,−4,…,4,5;=1,2,3),得到输出结果。给出3个变量的所有取值的组合可得=113=1 331个样本点。在输出上加入高斯随机误差项,=~{0,[0.1×std()]2}(其中,std()为输出的标准差),然后进行敏感性分析,所得结果如表1所示。
从表1可以看出:Morris与Variance-based敏感性结果基本一致,但Morris敏感性结果不能给出变量交互作用的具体效用,而Variance-based在给出变量单独作用及总作用的同时,可以给出变量交互的具体作用值。因存在交互项13和23,Variance-based得到其敏感性较大,而其他交互项的敏感性较小。
Morris敏感性分析方法的实际意义即对模型偏导数分布的一种体现。基于SVM建模,并采用Morris方法分析,具体结果见表2。由表2可以看到:Morris敏感性分析得到的均值和标准差与偏导数计算的均值与标准差基本一致。对于未知模型的数据,可以较真实地还原其模型在各样本处关于变量的偏导数分布,验证了Morris方法在非线性数据中使用时的正确性。

表1 仿真数据基于SVM建模测试结果(R2=0.985 5)

表2 仿真数据偏导数分布信息与Morris敏感性分析结果对照表
注:表中D与D分别为与标准化后的数据。
表3所示为仿真数据方差分解结果计算值与Variance-based敏感性分析结果对照表。表3验证了Variance-based敏感性方法的有效性,各分解部分对输出变量影响与方差分解结果基本吻合,说明其可以很好地计算各变量变化对输出变化的效应。
以对1分解为例,从模型角度出发,分解其单独作用且变量1=*不变时,其他变量变化时的均值;计算当变量1变化时,随之变化的方差(),则可以得到变量1单独作用占输出变异的比例()/Var(),简记为()/()。在计算1总作用时,首先计算其他变量不变时,1变化所引起输出变化的方差,并计算当其他变量变化时,随之变化的均值,得到(),则可以得到变量1总作用对输出变异的分解部分(),进而得到变量1总作用占输出变异的比例()/()。从表3可以看出:Variance-based敏感性分析结果体现了模型中输出变量的方差分解结果,()/()与方差分解中的一阶效应对应,而()/()与方差分解中的总效用对应。在实际生产中,因因变量间影响关系复杂,难以直接计算各变量的一阶效应和总效应,可采用Variance-based敏感性分析方法获得各变量及其耦合项对输出结果的方差波动的影响程度。
3.2 热轧板带凸度的敏感性分析
利用SVM对热轧板带出口凸度建模,输入变量如表4所示,其统计值如表5所示。输出变量为板带出口凸度,模型回归复测定系数为0.996 4,模型拟合效果良好。

表3 仿真数据方差分解结果计算值与Variance-based敏感性分析结果

表4 板带凸度数据集输入变量表

表5 变量统计值
在模型基础上进行敏感性分析,图1所示为Morris敏感性分析结果,横坐标为,代表输入变量对板带凸度的影响程度;纵坐标为,代表输入变量与其他输入变量交互作用对板带凸度的影响。从图1可以看出:相对于较小,表明变量间交互作用对板带凸度的影响并不明显,只有变量11,16,12,6和5(分别对应CROWN0,CROWN5,CROWN1,EPS1和EPS0)的交互作用影响较大。

图1 Morris敏感性分析μ−σ图
图2所示为Variance-based敏感性分析结果中变量总效应Ti,代表输入变量变化占引起的板带凸度变化的比例(总效应)。由图2可以看出:变量16,11,12,5和6(分别对应CROWN5,CROWN0,CROWN1,EPS0和EPS1)有着较明显的总效应,分别达到38.7%,21.7%,14.0%,10.3%和8.0%。
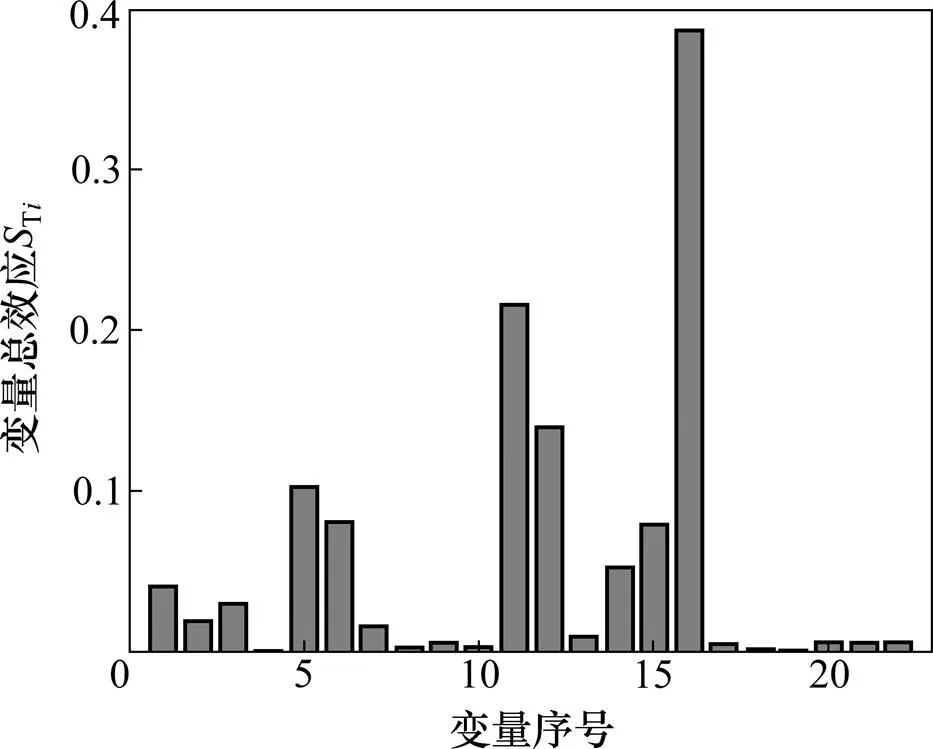
图2 Variance-based敏感性分析方法STi
Variance-based敏感性分析方法不仅给出了变量的总效应Ti,同时给出了变量单独作用或是变量交互作用的效应S。图3所示为根据Variance-based方法计算的S,绘制成的变量效应的灰度图(在此只给出二阶交互作用)。每个网格代表该网格所对应的横纵坐标,即2个变量交互作用下的效应(主对角线为该变量单独作用下的效应)。颜色越深,表明效应越强;反之,效应越弱。
图3直观地反映了变量及变量间交互作用的敏感性程度。每个方格代表其横纵坐标所对应变量的交互作用对板带凸度的影响,其中,对角线上方格代表其对应变量的单独作用。对角线颜色越深,表明效应越强,可以说明在变量的各个效应中,变量单独作用的效应占着主导地位。从其他位置的颜色深浅也可看出:5号和11号变量与其他变量之间的交互作用较明显,而其余变量间交互作用较弱。
利用分析结果中的及Ti对输入变量的敏感性进行排序,得到结果如表6所示。

图3 Variance-based敏感性分析方法Si灰度图
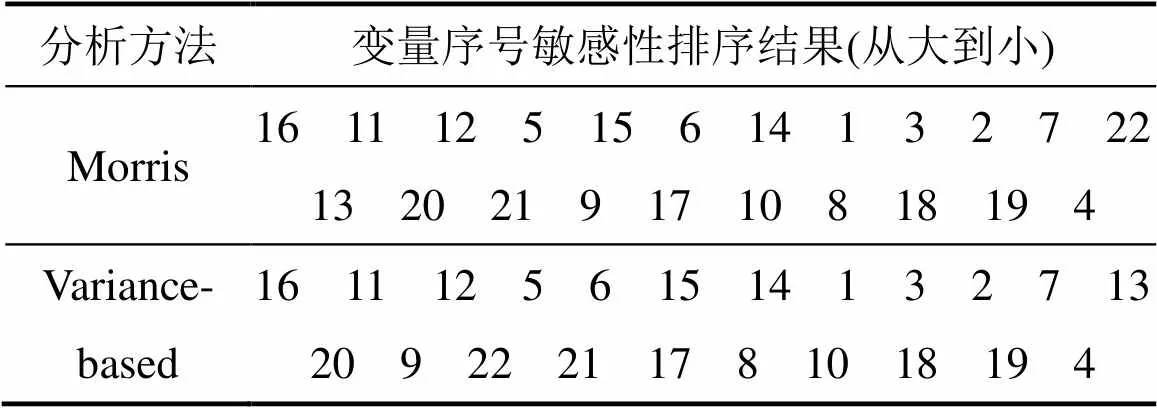
表6 凸度数据集变量敏感性排序
从表6可以看出:Morris方法和Variance-based方法的变量敏感性排序结果有较高的相似度,对凸度数据中变量的敏感性有近一致的评价,可有效地确定影响板带出口凸度的关键变量,为热轧板带的生产过程中工艺参数的调整提供参考。
4 结论
1) 基于SVM建模下进行的Morris和Variance-based敏感性方法均能很好地解释输入变量的敏感性问题,其中Morris方法更侧重于输入变量变化引起的输出变量变化(偏导数),而Variance-based方法更侧重于输出变量变化对各输入变量的分配(输入变量方差变化占引起的输出变量方差变化的比例)。
2) 针对板带出口凸度数据集,SVM建模下进行的Morris和Variance-based敏感性分析所得出的变量敏感性程度排序基本一致。综合2种方法,得出排名前5的变量为:机架5辊凸度、机架0辊凸度、机架1辊凸度、机架0压下率、机架1压下率。在生产过程中,应更重视对这些变量的监控与调整。因此,基于支持向量机的敏感性分析可为热轧板带的生产控制提供有效指导。
[1] 董永刚, 苏玉龙, 张岩岩. 配备组合式支承辊的四辊冷轧机辊系弹性变形数学模型[J]. 中南大学学报(自然科学版), 2013, 44(6): 2298−2302. DONG Yonggang, SU Yulong, ZHANG Yanyan. Mathematical model of elastic deformation of cold reduction mill equipped with composite back-up roll[J]. Journal of Central South University (Science and Technology), 2013, 44(6): 2298−2302.
[2] 曹建国, 张勇, 杨光辉, 等. UCM 六辊冷轧机中间辊辊形研究[J]. 中南大学学报(自然科学版), 2011, 42(4): 966−971. CAO Jianguo, ZHANG Yong, YANG Guanghui, et al. Intermediate roll contour of 6-hi UCM cold rolling mill[J]. Journal of Central South University (Science and Technology), 2011, 42(4): 966−971.
[3] 孔繁甫, 何安瑞, 邵健, 等. 板带轧机工作辊混合变凸度辊形研究[J]. 机械工程学报, 2012, 48(22): 87−92. KONG Fanfu, HE Anrui, SHAO Jian, et al. Research on mixed variable crown contour for work roll of strip mill[J]. Journal of Mechanical Engineering, 2012, 48(22): 87−92.
[4] 李洪波, 张杰, 曹建国, 等. 五次 CVC 工作辊辊形与板形控制特性[J]. 机械工程学报, 2012, 48(12): 24−30. LI Hongbo, ZHANG Jie, CAO Jianguo, et al. Roll contour and strip profile control characteristics for quintic CVC work roll[J]. Journal of Mechanical Engineering, 2012, 48(12): 24−30.
[5] TIBAR H, JIANG Z Y. Improving thin strip profile using work roll cross and work roll shifting methods in cold strip rolling[J]. International Journal of Metals, 2017, 2017(4): 1−10.
[6] CORTEZ P, EMBRECHTS M J. Using sensitivity analysis and visualization techniques to open black box data mining models[J]. Information Sciences, 2013, 225(4): 1−17.
[7] TAVAKOLI S, MOUSAVI A. Event tracking for real-time unaware sensitivity analysis (Event Tracker)[J]. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(2): 348−359.
[8] MORRIS T P, KAHAN B C, WHITE I R. Choosing sensitivity analyses for randomised trials: principles[J]. BMC Medical Research Methodology, 2014, 14(2): 571−575.
[9] WEI Pengfei, LU Zhenzhou, SONG Jiangwen. Variable importance analysis: a comprehensive review[J]. Reliability Engineering and System Safety, 2015, 142(12): 399−432.
[10] O'HAGAN A, BUCK C E, DANESHKHAH A, et al. Uncertain judgements: eliciting experts’ probabilities[M]. New York: John Wiley & Sons, 2006: 1−14.
[11] DING P, VANDERWEELE T J. Sensitivity analysis without assumptions[J]. Epidemiology, 2016, 27(3): 368−377.
[12] CAMPBELL J E, CARMICHAEL G R, CHAI T, et al. Photosynthetic control of atmospheric carbonyl sulfide during the growing season[J]. Science, 2008, 322(5904): 1085−1088.
[13] BAILIS R, EZZATI M, KAMMEN D M. Mortality and greenhouse gas impacts of biomass and petroleum energy futures in africa[J]. Science, 2005, 308(5718): 98−103.
[14] MARIO P. Sensitivity analysis in practice: a guide to assessing scientific models[J]. Journal of the American Statistical Association, 2006, 101(473): 398−399.
[15] EDELMIRA D G, SALVADOR F C R. Assessment of global sensitivity analysis methods for project scheduling[J]. Computers & Industrial Engineering, 2016, 93: 110−120.
[16] MARA T A, TARANTOLA S. Variance-based sensitivity indices for models with dependent inputs[J]. Reliability Engineering & System Safety, 2012, 107(11): 115−121.
[17] KUCHERENKO S, TARANTOLA S, ANNONI P. Estimation of global sensitivity indices for models with dependent variables[J]. Computer Physics Communications, 2012, 183(4): 937−946.
[18] TARANTOLA S, BECKER W, ZEITZ D. A comparison of two sampling methods for global sensitivity analysis[J]. Computer Physics Communications, 2012, 183(5): 1061−1072.
[19] SALTELLI I M S. Sensitivity analysis for nonlinear mathematical models: numerical experience[J]. Mathematical Modeling & Computational Experiment, 1995, 7(11): 16−28.
[20] HOMMA T, SALTELLI A. Importance measures in global sensitivity analysis of nonlinear models[J]. Reliability Engineering & System Safety, 1996, 52(1): 1−17.
[21] EMANUELE B, ELMAR P. Sensitivity analysis: a review of recent advances[J]. European Journal of Operational Research, 2016, 248(3): 869−887.
(编辑 刘锦伟)
Sensitivity analysis on influencing factor of strip crown in hot rolling
LIANG Bing1, 2, HE Fei1, 3, YANG Debin2, YANG Quan3, LIU Peng4
(1. Collaborative Innovation Center of Steel Technology,University of Science and Technology Beijing, Beijing 100083, China;2. School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China;3. National Engineering Research Center of Flat Rolling Equipment,University of Science and Technology Beijing, Beijing 100083, China;4. Shougang Research Institute of Technology, Beijing 100043, China)
In view of the hot rolling process, the sensitivity analysis on the influencing factor of strip crown based on the support vector machine was carried out. The support vector machine was adopted to establish the relationship model between process parameters and strip crown, then the key factors that affecting the strip crown were obtained by Morris and Variance-based sensitivity analysis methods. The results show that Morris and Variance-based sensitivity analysis methods based on the support vector machine can accurately locate the key factors, which provides guidance for the production control of the hot rolling process.
strip crown; sensitivity analysis; Morris; Variance-based
10.11817/j.issn.1672−7207.2018.02.013
TG335.5
A
1672−7207(2018)02−0353−07
2017−02−10;
2017−03−29
国家自然科学基金资助项目(51204018);国家“十二五”科技支撑计划项目(2015BAF30B01);北京高等学校青年英才计划项目(YETP0422);中央高校基本科研业务费资助项目(FRF-BR-17-030A)(Project(51204018) supported by the National Natural Science Foundation of China; Project(2015BAF30B01) supported by the National Key Technology R&D Program of the 12th Five-year Plan of China; Project(YETP0422) supported by the Beijing Youth Talents Program of University; Project(FRF-BR-17-030A) supported by the Fundamental Research Funds for the Central Universities)
何飞,博士,副研究员,从事生产过程质量建模、模式识别、板带控制研究;E-mail:hefei@ustb.edu.cn

