基于遗传算法的BP神经网络在水库月入库径流量预测中的应用

齐银峰，谭荣建

（昆明理工大学国土资源学院，云南省昆明市 650093）

0 引言

水库入库径流量预测是水库进行科学管理、搞好水库调度运用的重要依据，开展水库入库径流量预报对确保水库和下游安全、充分利用水资源、发挥水库的工程效益起着重要作用，具有重要的理论意义和实用价值[1]。一般来说，河流径流量预报的方法基本分为两种：一是过程驱动模型方法，该模型以水文学概念为基础，模拟河道的演变过程和径流的产流过程，以期对径流量的产生过程进行预报；二是数据驱动模型方法，该模型不研究水文系统的物理过程，将建立数据之间的最优数学关系作为模型的目标[2]。本文中采取的BP神经网络是基于数据之间的最优数学关系的预测方法。理论已经证明，BP神经网络只要有足够多的隐含层和隐节点，就可以以任意的精度逼近非线性映射关系[3]，其在处理高度非线性的水文系统时有着传统预测方法不可比拟的优势[4]。

1 BP神经网络

图1 3层BP神经网络结构Fig.1 3 layer BP neural network structure

BP（Back Propagation）神经网络是一种多层前馈神经网络，是一个3层的网络的拓扑结构，如图1所示，包括输入层、输出层和隐含层，各神经元与下一层的神经元全连接，同层神经元之间无连接。BP神经网络采用单隐层的三层前馈神经网络模型，学习规则为有导师的误差反向修正法，即以网络学习时输出层的输出与期望输出的误差为原则，将此误差沿输出层传递到隐藏层，再由隐藏层到输入层，通过误差的反向传播修正各连接层的连接权重和阈值，直到误差达到要求为止[5]。

定义误差的目标函数为：

式中 n——输入层神经元的个数；

yk——网络的期望输出值；

ŷk——网络的实际输出值。

反向传播（BP）神经网络的训练过程主要包括以下步骤：

（1）网络初始化：确定BP网络的输入层节点数n、隐含层结点数m、输出层结点数l，选定各节点之间的传递函数为Sigmoid函数，设定输入层与隐含层、隐含层与输出层神经元之间的连接权值分别为 Wij和 Wjk。

（2）隐含层输出计算：

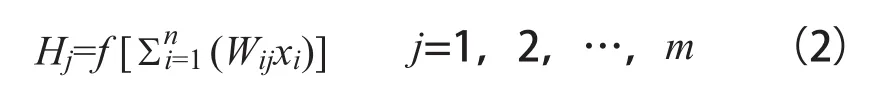
xi——第i个输入节点变量。

（3）输出层输出计算：

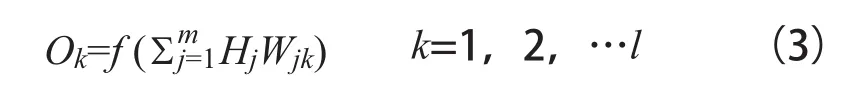
（4）修正连接权值：

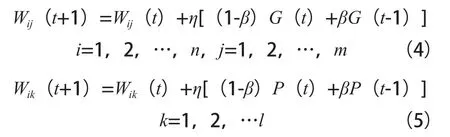
式中 η—— 学习速率，η＞0，G（t）=-∂E/∂Wij（t），P（t）=-∂E/∂Wjk（t）；

β——动量因子，0≤β＜1。

（5）判断目标函数的结果是否满足要求，当误差函数的值达到了预设的精度或者学习的次数超出设定的次数，则算法终止。否则，继续选取样本输入及样本对应的期望输出，返回到步骤（2）继续对网络进行训练，直至误差达标或学习次数达到预设值。

2 基于遗传算法的BP神经网络模型

遗传算法（Genetic Algorithm）是模拟进化论中的遗传选择和自然淘汰的生物进化过程的算法模型，在本质上是一种不依赖问题类型的直接搜索方法，属于启发式搜索算法。该算法首先生成一组候选解（初始种群），接着定义解空间的适应度函数（个体评价函数），并利用适应度函数求取候选解所对应的适应度，根据所求适应度决定保留其中某些候选解，而将另一些适应度低的候选解进行淘汰，然后对未被淘汰的候选解进行交叉和变异操作，生成新的候选解。再对这些新的候选解进行适应度选择，依次进行直至求得最优解[6]。

BP神经网络对于层与层之间初始的连接权值和阈值异常敏感，若初始参数的设置不合理，比较容易导致网络收敛速度慢和陷入局部最优解，因此本文将遗传算法和BP神经网络相结合，利用遗传算法来对BP神经网络的初始权值和阈值进行优化，以提高BP神经网络的收敛速度，同时减小BP算法陷入局部最优解的可能性[7-10]。

遗传算法与 BP 神经网络结合的数学表达为：

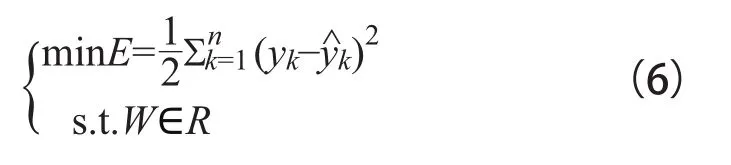
具体步骤为：

（1）设种群规模为P。随机生成P个个体的初始种群W=（W1，W2，…，Wp）T，选择一个数据范围，利用一般的线性插值函数在该范围内生成一个种群中个体Wi的实数向量w1，w2，…，ws，将其作为遗传算法的一个染色体。染色体包含了整个BP神经网络的所有权值和阈值。为了得到高精度权值和阈值，本文对染色体采用实数编码的方式进行编码，编码长度为：

式中 R——输入层节点数；

S1——隐含层节点数；

S2——输出层节点数。

（2）确定初始种群的适应度函数。 给定BP 神经网络的进化参数，将上一步中通过线性插值得到的实数向量作为遗传算法的染色体对BP神经网络的权值和阈值进行赋值，输入训练样本进行神经网络训练，达到设定的精度得到网络训练输出值，以BP神经网络的预测输出和期望输出之间的绝对误差平方和的倒数作为适应度函数。

（3）选择操作。采用比例选择方法选择算子，基于适应度比例的选择策略对每一代种群中的染色体进行选择。选择概率为：

式中 p——种群个体的数目；

Fi——个体i的适应度值。

（4）交叉操作。由于个体采用实数编码，交叉操作方法采用实数交叉法。第k个基因gk和第l个基因gl在j位的交叉操作分别为：

式中 b——［0，1］之间的随机数。

（5）变异操作。以一个比较小的变异概率选择第i个个体的第j个基因gij进行变异从而增加种群的多样性，变异操作方法为：

以上式中 r1——[0，1]之间的随机数；

gmax、gmin——gij的上、下限 ；

r2——一个随机数；

s——当前迭代次数；

smax——最大进化代数。

（6）计算适应度函数的值，若满足算法预设的结束条件，则将优化后的神经网络的权值和阈值进行输出，否则返回（3）继续进行迭代，直至满足结束条件。

（7）以遗传算法输出的优化的权值和阈值作为BP神经网络的初始权值和阈值，用训练样本对 BP神经网络进行训练，得到水库入库流量预测模型。

3 应用实例及其结果分析

本文数据来源于某水库多年来的入库径流量记录，根据相关资料分析可知，影响该水库入库径流量的主要因素为该水库上游流域的月降水量、平均气温、蒸发量、平均湿度等，这些主要影响因素的值可由该水库上游的多个水情监测站所记录的多年多期数据获得。将这些数据作为BP神经网络的学习样本，并将所有58个样本分为训练样本和测试样本，其中48个作为训练样本，10个作为测试样本。

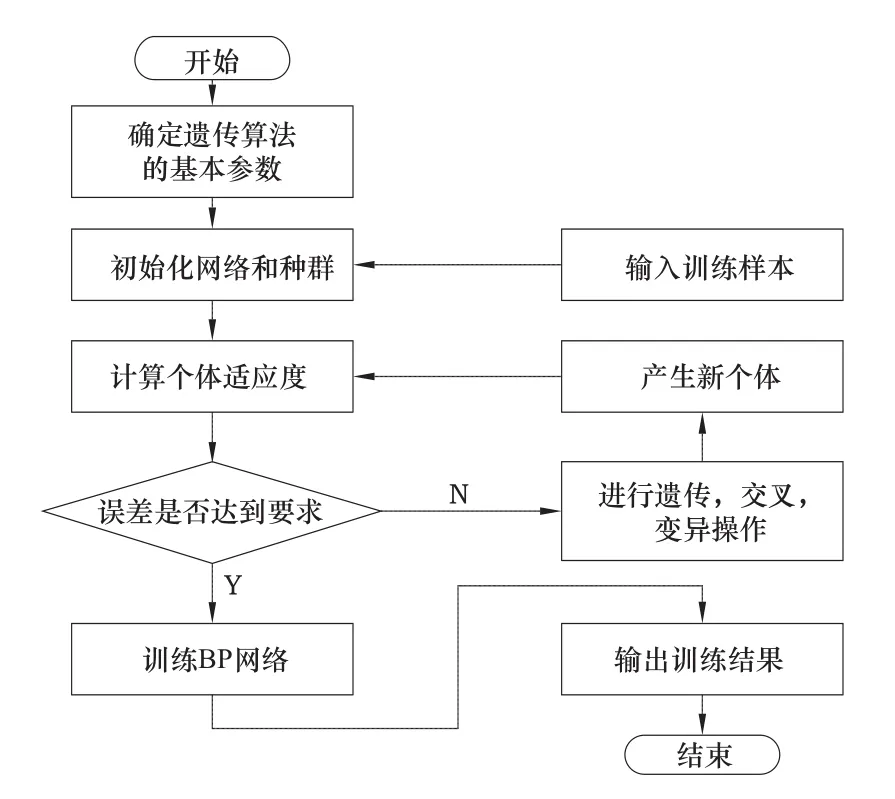
图2 GA-BP算法流程Fig.2 GA-BP algorithm flow

3.1 数据的处理和GA-BP网络模型参数设定

3.1.1 数据的归一化

数据的归一化是将有量纲经过变换化为无量纲的方法。数据归一化处理有利于BP神经网络的训练速度，加快网络的收敛进程。本文采用最大最小值法对数据进行归一化处理。

3.1.2 BP网络模型参数设定

选定BP神经网络的结构参数和训练参数对网络进行训练。神经网络输入层节点的数目为4个，输出节点数目为1个。隐含层节点数对BP神经网络预测精度有较大的影响：节点数太少，网络不能充分的学习，需要增加训练次数，训练的精度也会受到影响；节点数太多则训练的时间增加，网络容易过拟合。最佳隐含层节点数的选择参考如下公式：

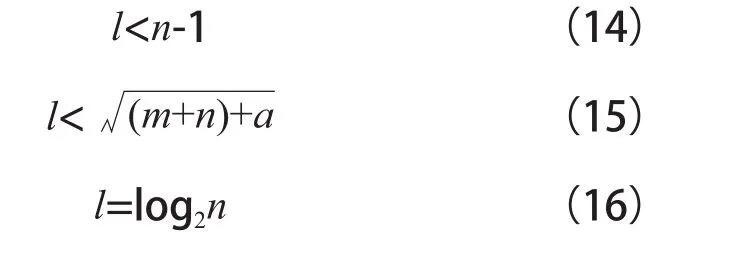
式中 n——输入层节点数；

l——隐含层节点数；

m——输出层节点数；

a——0～10之间的常数。

结合以上经验公式来确定隐含层节点数的大概范围，然后用试凑法来确定隐含层的最佳节点数。本例中设定神经网络的数目为5个，隐层和输出层均采用Sigmoid传输函数，设定训练函数为自适应调整学习速率附加动量因子梯度下降反向传播算法训练函数，设定神经网络训练的目标误差为0.001，最大训练步数为2000，学习速率为0.01。训练结束后，将模型的输出数据反归一化到原来的数据范围。

3.1.3 遗传算法优化BP神经网络初始权值和阈值

把遗传算法用于BP神经网络的训练，利用遗传算法全局搜索的特性，得到一个初始的权值矩阵和初始的阈值向量，再用BP神经网络算法得到最终的GA-BP神经网络。选择遗传算法初始的种群数目为50。交叉概率用于控制交叉操作的频率，不可过大也不可过小，交叉概率过大会使得种群中个体的更新过快，而将适应度高的个体淘汰掉，交叉概率过小会使搜索缓慢甚至停止，故选择交叉概率为 0.5，变异概率过大大会使搜索趋于随机化，过小也影响下一代个体的产生，因此选择变异概率为0.03。遗传算法的主要参数如表1所示。

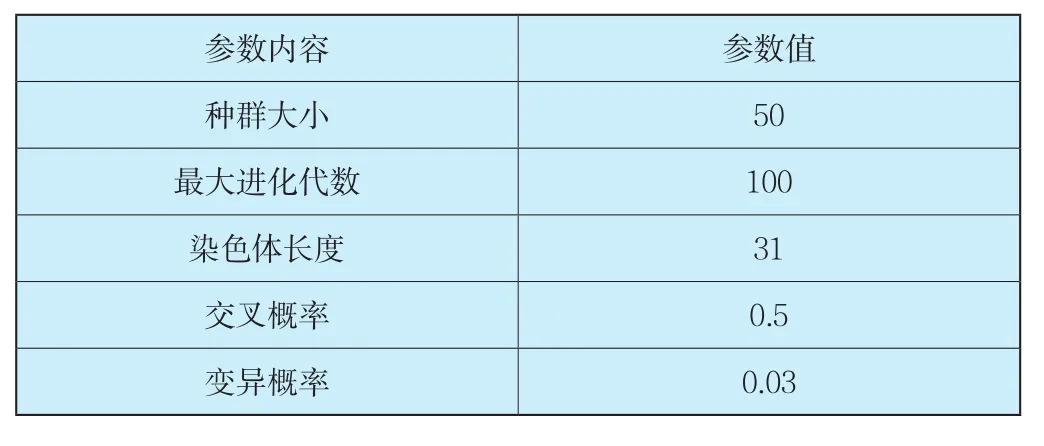
表1 遗传算法的主要参数Tab.1 Main parameters of genetic algorithm

3.2 遗传算法优化BP神经网络训练及结果输出

经过遗传算法优化的BP神经网络，其具有了更为恰当的初始的权值和阈值，提高了BP神经网络的收敛速度。将采集的48组训练数据输入模型进行训练，训练的结果如图3和图4所示。

BP网络预测与GA-BP预测结果对比如图4所示。

3.3 误差分析与算法评价指标对比

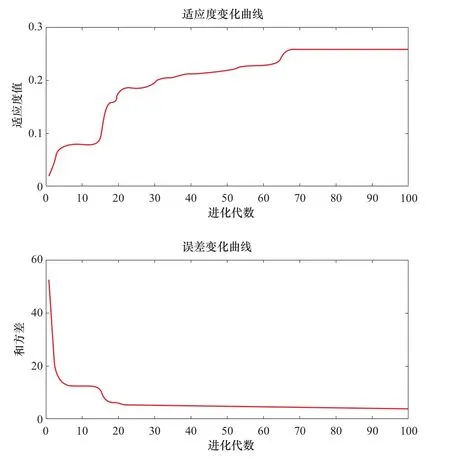
图3 GA-BP算法适应度与误差变化曲线Fig.3 The fitness of GA-BP algorithm and the curve of error change

图4 BP网络预测与GA-BP预测情况对比Fig.4 Comparison between BP network prediction and GA-BP prediction

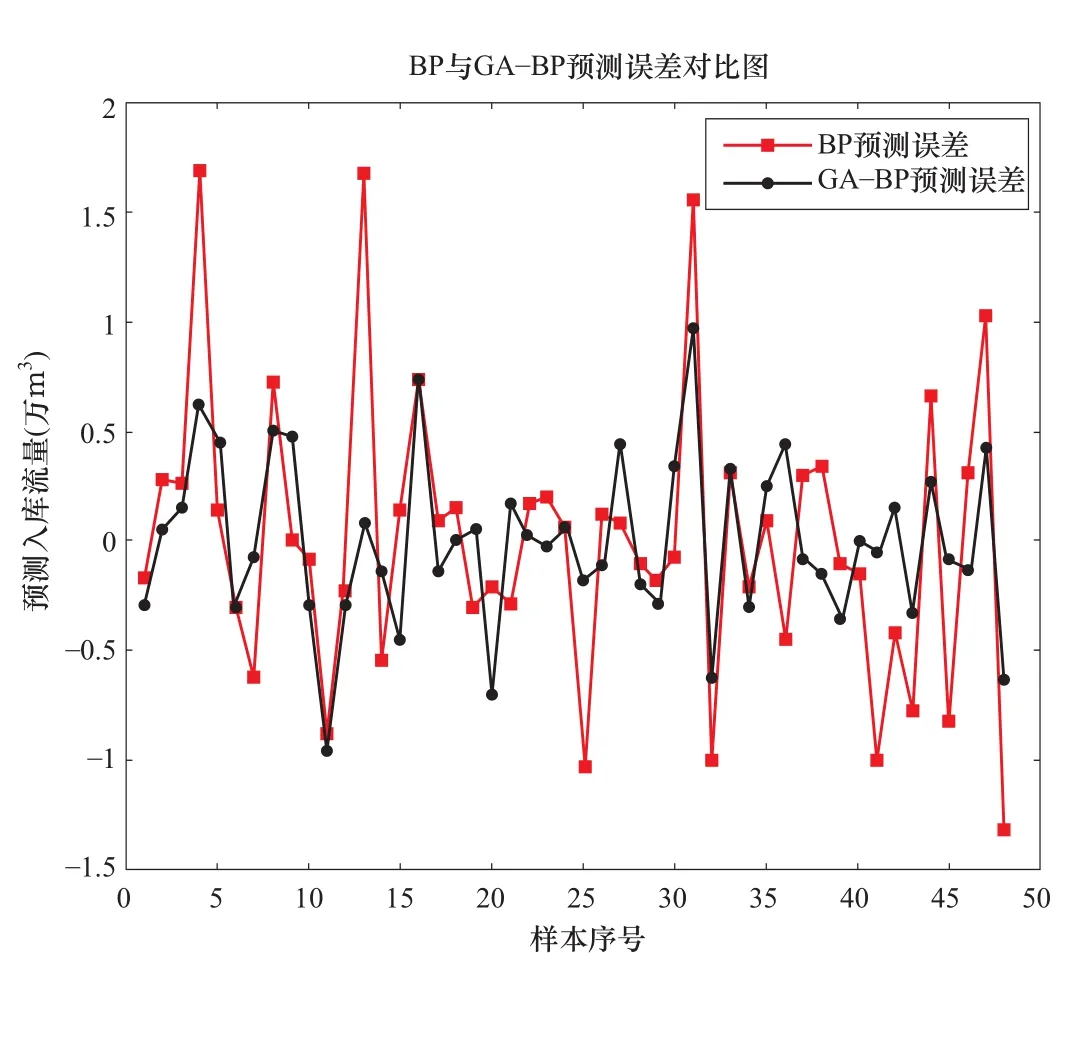
图5 BP网络预测与GA-BP预测误差对比Fig.5 Comparison between BP network prediction and GA-BP prediction error

将两种方法的预测误差进行对比分析，并将评价算法优劣的其他几个因素也进行对比。BP网络预测与GA-BP预测误差对比结果如图5所示，BP网络预测与GA-BP预测误差百分比对比结果如图6所示。

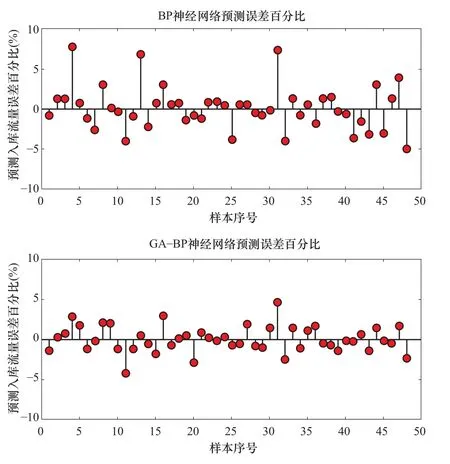
图6 BP网络预测与GA-BP预测误差百分比Fig.6 BP network prediction and the percentage of GA-BP prediction error

将两种方法的预测误差数值进行对比分析，并将评价算法优劣的几个主要指标也进行对比。利用10个测试样本对BP网络预测与GA-BP预测误差数值进行对比，对比分析结果如表2所示，BP网络预测与GA-BP预测性能对比结果如表3所示。

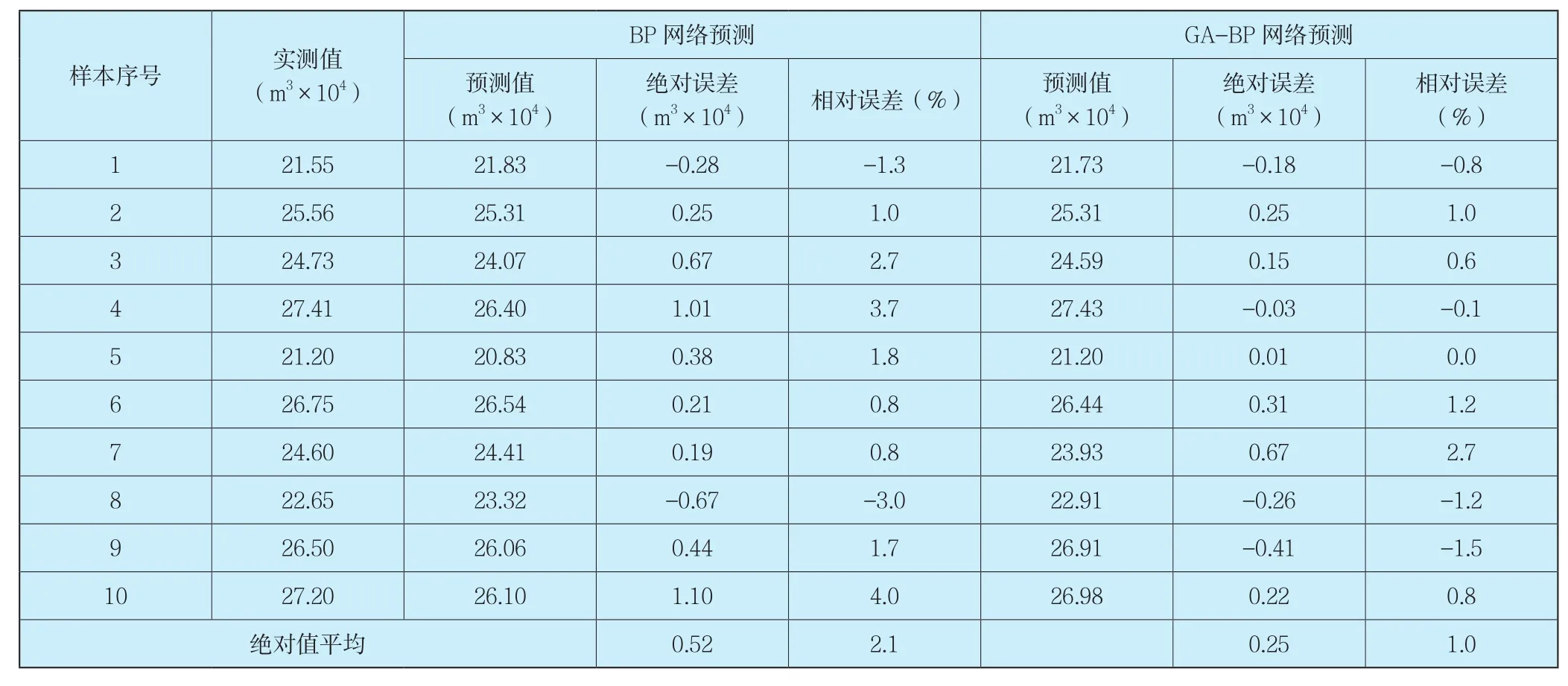
表2 10个测试样本的BP神经网络与GA-BP预测误差对比Tab.2 Comparison between BP neural network and GA-BP prediction error of 10 test samples

表3 BP神经网络与GA-BP算法评价指标比较Tab.3 Comparison of evaluation indexes between BP neural network and GA-BP algorithm

4 结束语

本文将遗传算法与BP神经网络相结合建立水库月入库径流量的预测模型，以影响水库月入库径流量的几个因素的历史数值作为BP神经网络预测模型的输入变量，水库月入库径流量的历史数值作为模型的输出变量，利用遗传算法特有的全局搜索能力优化了BP神经网络的初始权值和阈值。采用优化后的BP神经网络建立水库月入库径流量预测模型。实验结果表明，遗传算法结合BP网络的模型相较于单独的BP神经网络具有预测精度较高、收敛速度较快的优点。

[1]吴彬.浅谈水库水文预报基本资料的搜集[J].科技信息，2009，11:733.

WU Bin. Discussion on the collection of basic data of reservoir hydrology forecast[J]. Science & Technology Information，2009，11:733.

[2]屈磊磊，齐丽岩，高胜哲.时间序列分析在径流预测中的应用[J].安徽农业科学，2015，21:23-24+103.

QU Leilei，QI Liyan，GAO Shengzhe. Application of time series analysis in runoff forecasting[J]. Journal of Anhui Agricultural Sciences ，2015，21:23-24+103.

[3]颜七笙，游泳，杨志辉. BP网络结构设计与算法探讨[J].科技广场，2005，03:36-38.

YAN Qisheng，YOU Yong，YANG Zhihui. Design and algorithm of BP network structure[J]. Science Mosaic，2005，03:36-38.

[4]杨鑫，任海霞，万芳.水库径流预报的蚁群优化神经网络算法应用研究[J].中国农村水利水电，2013，12:9-12+18.

YANG Xin，REN Haixia，WANG Fang. Study on the application of ant colony optimization neural network algorithm for reservoir runoff forecasting[J]. China Rural Water and Hydropower，2013，12:9-12+18.

[5]程向军，神经网络原理及其应用[M]. 北京: 国防工业出版社，1995:1-300.

CHENG Xiangjun. The principle and application of neural network[M]. Beijing: National Defense Industry Press，1995:1-300.

[6]周明，孙树栋. 遗传算法原理与应用[M]. 北京: 国防工业出版社，1999:32-64.

ZHOU Ming，SUN Shudong. The principle and application of genetic algorithm[M]. Beijing: National Defense Industry Press，1999:32-64.

[7]黄建国，罗航，王厚军，龙兵.运用GA-BP神经网络研究时间序列的预测[J].电子科技大学学报，2009，05:687-692.

HUANG Jianguo，LUO Hang，WANG Houjun，LONG Bing. Application of GA-BP neural network to study time series prediction[J]. Journal of University of Electronic Science and Technology of China，2009，05:687-692.

[8]谷晓平，王长耀，袁淑杰.GA-BP神经网络模型在流域面雨量预报的应用研究[J].热带气象学报，2006，03:248-252.

GU Xiaoping，WANG Changyao，YUAN Shujie. Application of.GA-BP neural network model to rainfall forecast of basin surface[J]. Journal of Tropical Meteorology，2006，03:248-252.

[9]都晨. 基于模糊聚类的GA-BP风电场短期风速及功率预测的研究[D].南京理工大学，2013.

DU Chen. short-term prediction research of wind power based on Fuzzy Clustering algorithm and GA-BP[D]. Nanjing University of Science and Technology，2013.

[10]郭海湘，诸克军，胡杰，刘婷.GA-BP嵌套算法的理论及应用[J].数学的实践与认识，2008，01:116-125.

GUO Haixiang，ZHU Kejun，HU Jie，Liu Ting. The theory and application of GA-BP nested algorithm [J].Mathematics in Practice and Theory，2008，01:116-125.

齐银峰（1992—），男，在读硕士，主要研究方向：机器学习算法在工程实践中的应用。E-mail：443518908@qq.com

谭荣建（1965—），男，副教授，硕士生导师，主要研究方向：测绘及土地资源管理方面的学习与研究。E-mail：bcys5502@163.com