电磁轴承实现振动姿态解耦的转子不平衡抑制
,,
(浙江理工大学信息学院,杭州 310018)
0 引 言
主动电磁轴承具有无摩擦、无需润滑、适用高速场合、可实现转子振动主动控制等优良特性,发展前景十分广阔。由于加工精度以及材质不均匀等原因,实际转子或多或少地存在质量不平衡。转子不平衡力与转速的平方成正比,随着转速增大,不平衡力使得转子的旋转精度无法得到保证,甚至影响到电磁轴承转子系统的安全运行。因此,对磁悬浮转子的不平衡振动控制进行研究显得尤为重要。Vahedforough等[1]提出了一种改进的自适应强制平衡方法,该方法能够同时对正弦干扰的幅值和频率进行估算。Schuhmann等[2]提出利用卡尔曼滤波器和最优反馈的方法对转子进行不平衡控制。Jiang等[3]通过识别转子的不平衡质量,使电磁轴承生成相应的控制信号对转子进行不平衡补偿,该方法对转速变化不敏感,控制相对稳定。房建成等[4]对含多振动源的磁悬浮刚性转子进行动力学建模,并总结出主动振动控制所需完成的任务。黄立权等[5]建立了以转子振动响应为指标、磁极线圈电流幅值和相位为寻优参数的寻优控制模型,并提出相位整周搜寻算法。韩辅君等[6]提出了考虑电磁力影响的转子系统整体动平衡方法,实验结果表明平衡精度得到提高。蒋科坚等[7]通过施加试探信号并检测位移响应变化,直接识别出不平衡干扰的傅里叶参数。王秋晓等[8]提出了一种能够分离平动与摆动的振动测量机构,将弱的离心力从强的力矩中分离出来,并且避免了振动中心不确定问题。章琦等[9]通过坐标变换让PD控制算法直接对质心坐标进行调节,并通过仿真证明该方法可对锥动和平动模态进行解耦控制,但实际中质心位置往往未知,且PD参数不易调节。徐宾刚等[10]提出了测点模态比的概念,分析了测点模态比获取的可能性及方法,并将测点模态比应用于结构非对称柔性转子的全息动平衡。Shahgholi等[11-12]的研究表明,弯曲刚度、质偏心以及外阻尼等对非对称转子的动态性能有显著影响。徐鑫莉[13]对质偏的各种测量方法及精度进行了分析,并着重研究了复摆测量法。
在电磁轴承转子的运动解耦控制的文献中,往往在假设转子的质心轴向位置已知的前提下设计控制算法,而实际中很难直观确定质心位置。本文提出了一种基于振动姿态解耦的电磁轴承转子补偿控制方法,首先通过振动识别获取转子的质心轴向位置,然后根据质心轴向位置进行平动和锥动姿态的解耦,其次依据这两种振动姿态对补偿信号进行搜寻,最后用电磁轴承产生的力和力偶分别予以控制,达到抑制不平衡振动的目的。
1 转子不平衡补偿原理
主动电磁轴承-转子控制系统原理图如图1所示,控制器根据x和y方向位移传感器检测的转子实时位置信号,产生相应的控制信号驱动功率放大器及电磁轴承,形成相互正交的可调电磁力,最终使得转子悬浮在轴承中心位置。
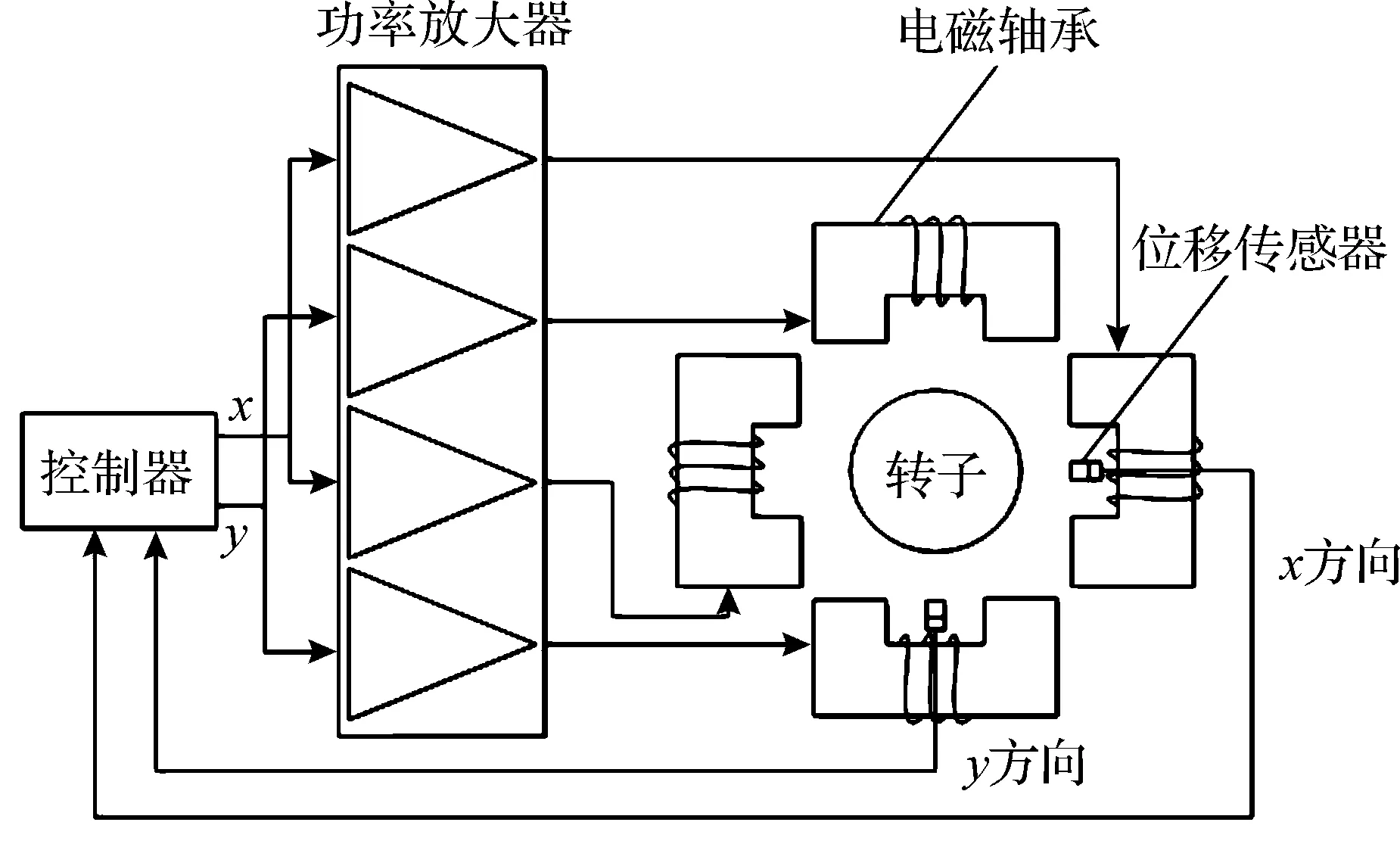
图1 主动电磁轴承-转子控制系统原理
在转子运行时,不平衡质量形成沿轴向分布的空间离心力系。刚性转子的离心力系可以向质心简化为一个不平衡力和一个不平衡力偶[14]。从而,转子的振动分解为质心的平动和绕质心的锥动。
在主动电磁轴承的应用中,可以将功率放大器和电磁轴承视作电磁力执行装置,通过在功放输入端叠加补偿信号来对转子施加补偿电磁力。当在电磁轴承x和y方向的功放输入端分别叠加余弦和正弦激励信号时,会对转子形成一个旋转矢量电磁力。而转子不平衡力同样为旋转矢量,故可通过协调补偿信号来控制补偿电磁力大小、方向和旋转速度,最终抵消不平衡力和不平衡力偶对转子的影响。不平衡力消除的表现为平动消除,不平衡力偶消除的表现为锥动消除。因此,转子不平衡补偿问题在本质上可归结为分别以平动和锥动偏移量为寻优目标,补偿信号的幅值和相位作为寻优参数的寻优控制问题。
2 振动姿态解耦控制模型
根据转子动力学理论,刚性转子在空间的运动可描述为在2个径向和1个轴向的平移以及绕这3个轴的旋转。图2为刚性转子的空间运动姿态模型,设O是转子质心投影到形心轴上的点,z轴为理想的转子旋转轴,质心到两个轴承面的距离分别为la和lb,两轴承间距为l=la+lb,径向电磁轴承的等效刚度和阻尼分别为ke和de。设转子广义位移q=(x,β,y,-α)T,其中x、y是转子在对应方向上的位移,β是转子绕y轴的逆时针转角,α是转子绕x轴的逆时针转角。另设两端磁轴承的转子位移qB=(xa,xb,ya,yb)T,悬浮控制器提供的电磁力为f=(fxa,fxb,fya,fyb)T,令Ke=diag(ke,ke,ke,ke),De=diag(de,de,de,de),则
(1)
q=TqB
(2)
式中T为位移变换矩阵:
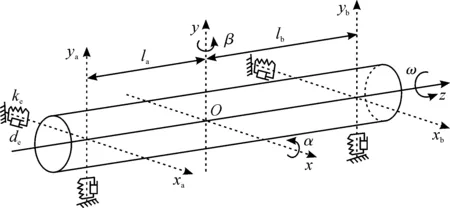
图2 刚性转子空间运动姿态模型
设转子质量为m,转子旋转角速度为ω,赤道转动惯量为J,极转动惯量为Jz,x方向的外力和外力矩分别为Fx和Mx,y方向的外力和外力矩分别为Fy和My。转子运动方程可表示为:
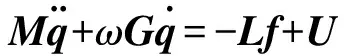
(3)
式中:U=(Fx,Mx,Fy,My)T;M,G,L分别为转子质量矩阵、陀螺矩阵、力臂矩阵:
将式(1)、(2)代入(3),整理可得:
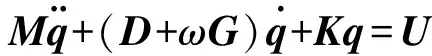
(4)
式中:D=LDeT-1,K=LKeT-1.
下面讨论振动姿态解耦控制的补偿电流的施加方式。设iB=(ixa,ixb,iya,iya)T,Ki=diag(ki,ki,ki,ki)分别为径向电磁轴承的振动补偿电流,电流刚度系数矩阵。则施加振动补偿电流后的转子运动方程为:
(5)
等式两端分别为转子广义位移和振动补偿电流的函数。
本文在式(5)的基础上,以转子广义位移最小化为目标,搜寻产生振动补偿电流。基于转子广义位移(x,β,y,-α)T,定义平动和锥动价值函数:
(6)
(7)
搜寻算法将q作为输入信号,依据εp和εz的变化情况搜寻质心处转子广义位移对应的补偿电流信号i。由于力臂矩阵L的作用是将两端电磁轴承信号转化为作用于转子质心的力矩信号,反之,搜寻算法得到的质心处补偿信号可通过其逆阵L-1分配到两端电磁轴承,故iB具有如下形式:
iB=L-1i
(8)
从物理意义的角度分析,因为实际中的控制信号必须通过两端电磁轴承施加,所以矩阵L-1的作用是将质心处的控制信号转化为两端电磁轴承的控制信号。
通过以上分析可知,振动姿态解耦控制模型的整体思路是先通过坐标变换将两端轴承处位移转化为质心处转子广义位移,从而控制算法可分别对质心处转子广义位移中的平动成分和锥动成分进行调节,之后再通过坐标变换将质心处控制信号分配到两端轴承处。振动姿态解耦控制模型如图3所示,图中iB′为iB在功率放大器输入端的等效信号。
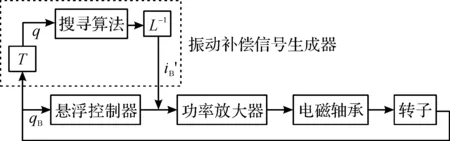
图3 振动姿态解耦控制模型
3 质心轴向位置的获取
由于转子不平衡质量的随机分布和转子系统结构的非对称设计等原因,转子的质心轴向位置往往偏移两轴承的轴向中点,但位移变换矩阵和力臂矩阵都需要确定质心轴向位置。本文提出基于振动识别的转子的质心轴向位置获取方法。已有的研究表明,当转子处于静态悬浮时,两个互相垂直的径向平面之间的运动耦合可以忽略,并结合式(1),此时式(3)可表示为:
(9)
在转子静态悬浮下对x方向径向平面进行激振测试,根据式(9),转子系统在x方向的运动方程为:
(10)
其中:第一式是平动方程;第二式是转动方程。设质心轴向偏移为Δl,且la=0.5l+Δl,lb=0.5l-Δl,又根据式(2)可得x=(lbxa+laxb)/l,代入式(10)第一式,整理可得:
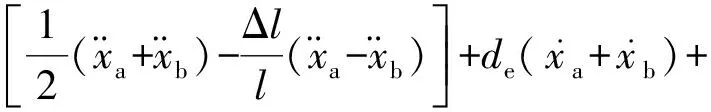
ke(xa+xb)=Fx
(11)
式中激励力和转子响应在激振测试中是已知量,在一端轴承处向转子施加正弦激励力,记作:
Fx=αFsinΩt+βFcosΩt
(12)
式中:Ω是正弦激励力的角速度;αF和βF是其傅里叶系数。转子位移响应记作:
(13)
式中:αa和βa是位移响应xa的傅里叶系数;αb和βb是位移响应xb的傅里叶系数。将式(12)、(13)代入式(11),可得:
(14)
如果在原激励力[αF,βF]值上试探性的叠加一个预设改变量[ΔαF,0],且因此产生的位移响应改变量为[Δαa,Δβa]、[Δαb,Δβb],则根据式(14)第一式,有:
deΩ(βa+Δβa+βb+Δβb)=αF+ΔαF
(15)
式(15)与式(14)第一式的两端同时相减,可得:
deΩ(Δβa+Δβb)=ΔαF
(16)
即可获得转子的质心轴向偏移:
(17)
4 搜寻算法
为了兼顾搜索精度与搜索速度,采用变步长方案,即振动较大时采用大步长提高搜索速度,振动较小时采用小步长提高搜索精度。定义搜寻步长矢量:
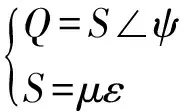
(18)
式中:ε为振动偏移量,μ为步长因子,S为搜寻步长,ψ为搜寻方向。搜寻方向按固定的顺序(0,π/2,π,-π/2)在四个方向依次轮序调节。
设n时刻补偿参数矢量为Cn,n时刻步长矢量为Qn,n时刻振动偏移为εn。设置初始值C0=0,Q0=S∠0,原始偏移量为ε0。在Cn上叠加Qn得到n+1时刻的补偿参数矢量Cn+1,即:
Cn+Qn=Cn+1
(19)
获取Cn+1对应的偏移量εn+1,若εn+1<εn,表明搜寻方向正确,继续执行上一个步长向量;若εn+1≥εn,表明搜寻方向错误,更改步长向量的方向。具体的执行策略如下:
(20)
补偿参数矢量尖端的搜寻轨迹如图4所示,搜寻轨迹最终会在目标矢量尖端的周围形成边长为2倍搜寻步长的方形轨迹。搜寻步长的取值与实际位移等效到系统中的取值范围有关,搜寻步长的选取原则是尽量取小值,有益于提高补偿参数的精度,但要求大于系统噪声值,以保证叠加的步长矢量能被检测到。本文实验在此原则的基础上取得了良好的补偿效果。
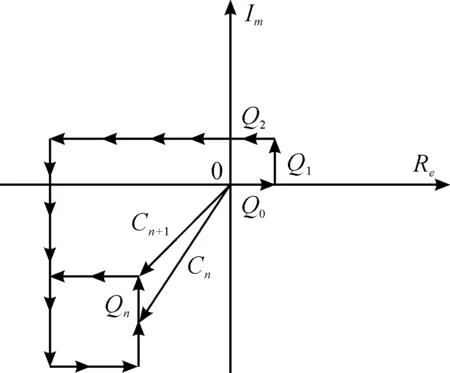
图4 复平面上参数搜寻示意图
图5为振动补偿信号生成器,图中Ap和θp为根据εp搜寻得到的幅值和相位,Az和θz为根据εz搜寻得到的幅值和相位。生成器输出的振动补偿信号iB′=(ixa′,ixb′,iya′,iya′)T,可表示为:
(21)
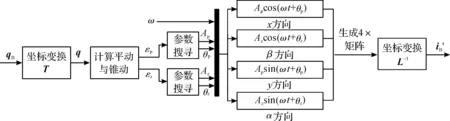
图5 振动补偿信号生成器
补偿信号iB′经过功率放大器与电磁轴承两个环节后,在转子两端形成旋转矢量电磁力,最终消除转子的平动和锥动。其实质是利用可控电磁力对转子不平衡力和不平衡力偶分别予以补偿,达到不平衡振动解耦控制的目的。
5 实验与结果分析
5.1 实验平台
实验平台为主动电磁轴承转子系统,如图6所示,该转子系统为粗短结构,其弯曲模态远高于工作转速,可视为刚性转子系统。转子径向由左右两个电磁轴承支承,轴向通过柔性联轴器与驱动电机相连。两端轴承的x和y方向分别放置电涡流位移传感器来检测转子位移信号。悬浮控制器采用4自由度的分散PID控制,控制和测量系统的采样频率为10 kHz。转子的质量m=9.92 kg,悬浮气隙为0.5 mm,电流刚度系数ki=40.3 N/A,两轴承间距l=300 mm。电磁轴承x方向在20 Hz频率下的等效刚度ke=2.32×105N/m,等效阻尼de=325 N·s/m。实验分为转子质心轴向位置测量实验和不平衡补偿实验两部分。

图6 主动电磁轴承转子系统实验平台
5.2 转子质心轴向位置测量实验
转子质心轴向位置测量实验需要前后两次对转子施加激励力,本文选取Ω=40π rad/s(20 Hz)的正弦激励力。通过一端磁轴承向转子施加第一次激励力,检测转子两端轴承处的位移响应,记录第一次激励和响应数据;改变激励力的傅里叶系数,向转子施加第二次激励力,检测转子两端轴承处的位移响应,记录第二次激励和响应数据;计算两次激励力的以及两次位移响应的傅里叶系数之间的差值。实验数据如表1所示。
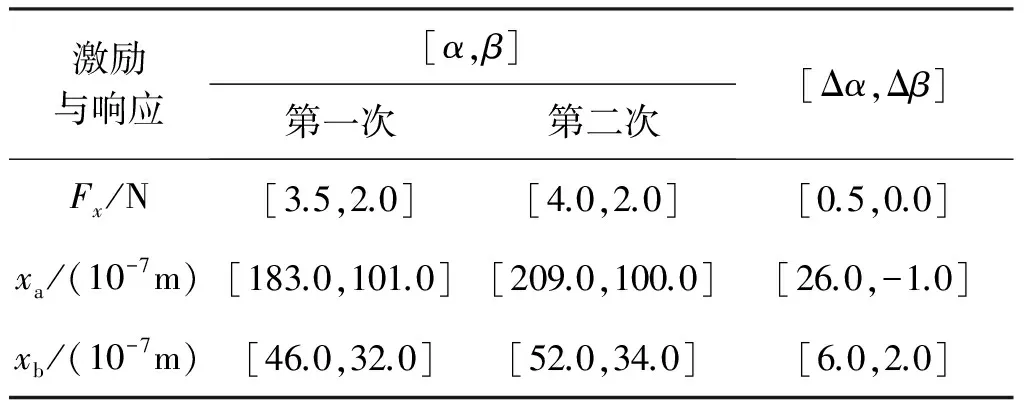
表1 测量实验中的激励力与位移响应数据
将实验数据代入式(17),获取转子的质心轴向偏移Δl=0.04l,从而可得la=0.54l,lb=0.46l。
5.3 转子不平衡补偿实验结果
本实验的目的是验证本文提出的方法对不平衡抑制的有效性。经测试,转子系统在1500 r/min(25 Hz)转速下的平动和锥动都较为明显,故为取得较好的实验效果,不平衡补偿实验选择工作转速为1500 r/min。
补偿参数的搜寻过程可以通过振动幅值的变化轨迹来反映,补偿参数与振动幅值是一一对应的,振动的收敛意味着补偿参数的收敛。
图7为转子平动与锥动的控制收敛过程。图7(a)中的两条实线分别对应两端轴承处的平动幅值下降过程,x、y轴表示相应方向上的平动幅值,虚线绘制的大小圆柱分别对应控制前后的平动偏移量。图7(b)中的两条实线分别对应两端轴承处的锥动幅值下降过程,x、y轴表示相应方向上的锥动幅值,虚线绘制的大小倒锥分别对应控制前后的锥动偏移量。可见,平动与锥动得到有效补偿,即补偿参数最终收敛。
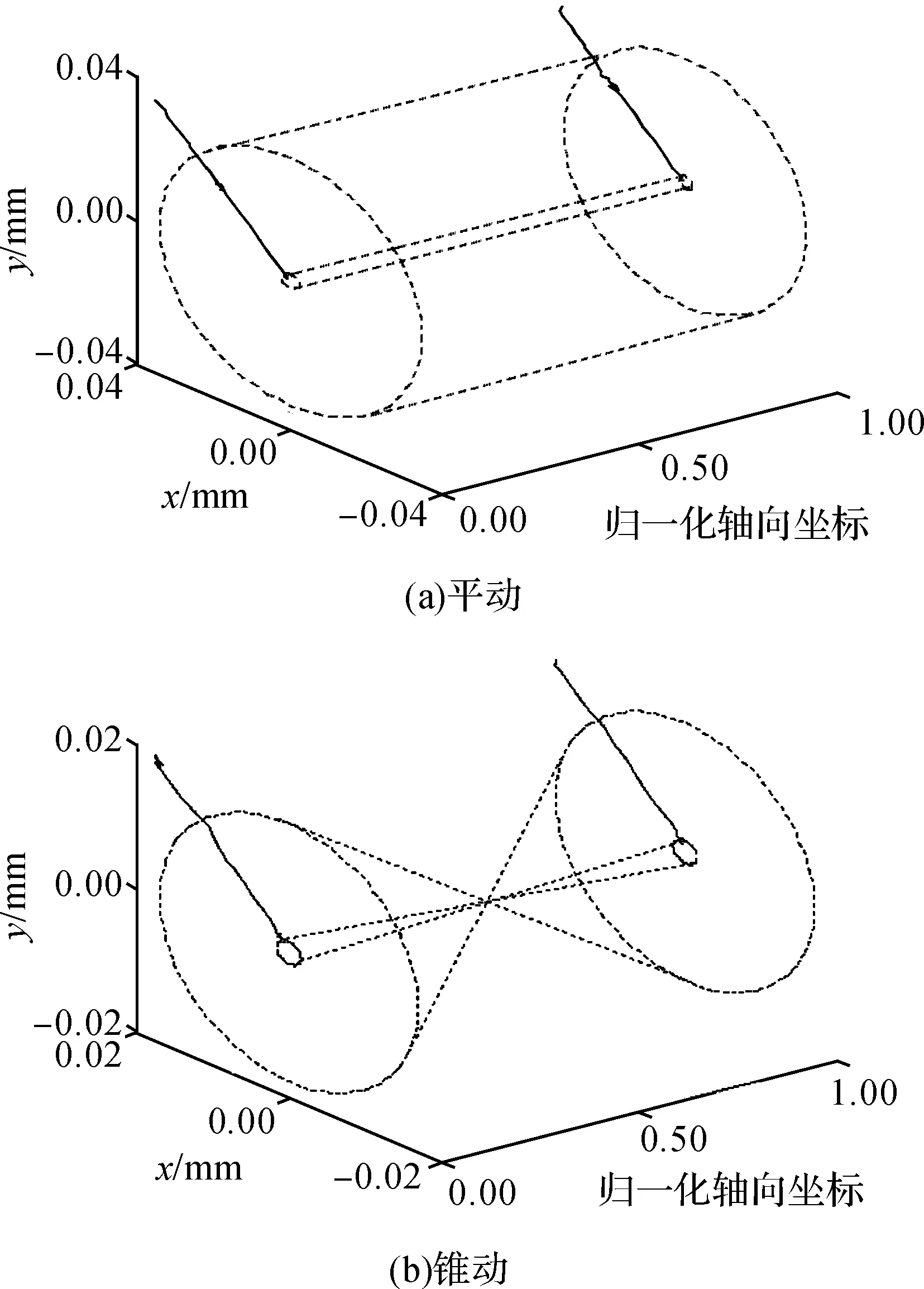
图7 两种振动姿态的控制收敛过程
不平衡振动的控制效果可以依据转子的运动轨迹以及振动功率谱的幅值进行量化评价。
图8是转子转速1500 r/min下,左侧轴承处位移传感器检测到的转子运动轨迹。不平衡补偿前,转子在x和y方向都有振动分量,这使得转子轴心轨迹呈现环形,位移波动峰-峰值达0.12 mm。不平衡补偿后,转子轴心的运动轨迹明显向中心收拢,补偿效果相当显著。因右侧轴承处的转子运动轨迹与之类似,不再赘述。
图9是不平衡补偿前后的转子振动功率谱图。可见,实施补偿前,振动功率谱在转速频率25 Hz处出现明显峰值,峰值大小为-11 dB。实施补偿后,转速频率处的振动幅值降低到噪声水平,约下降了40 dB。这说明转子不平衡抑制达到了很好的效果。
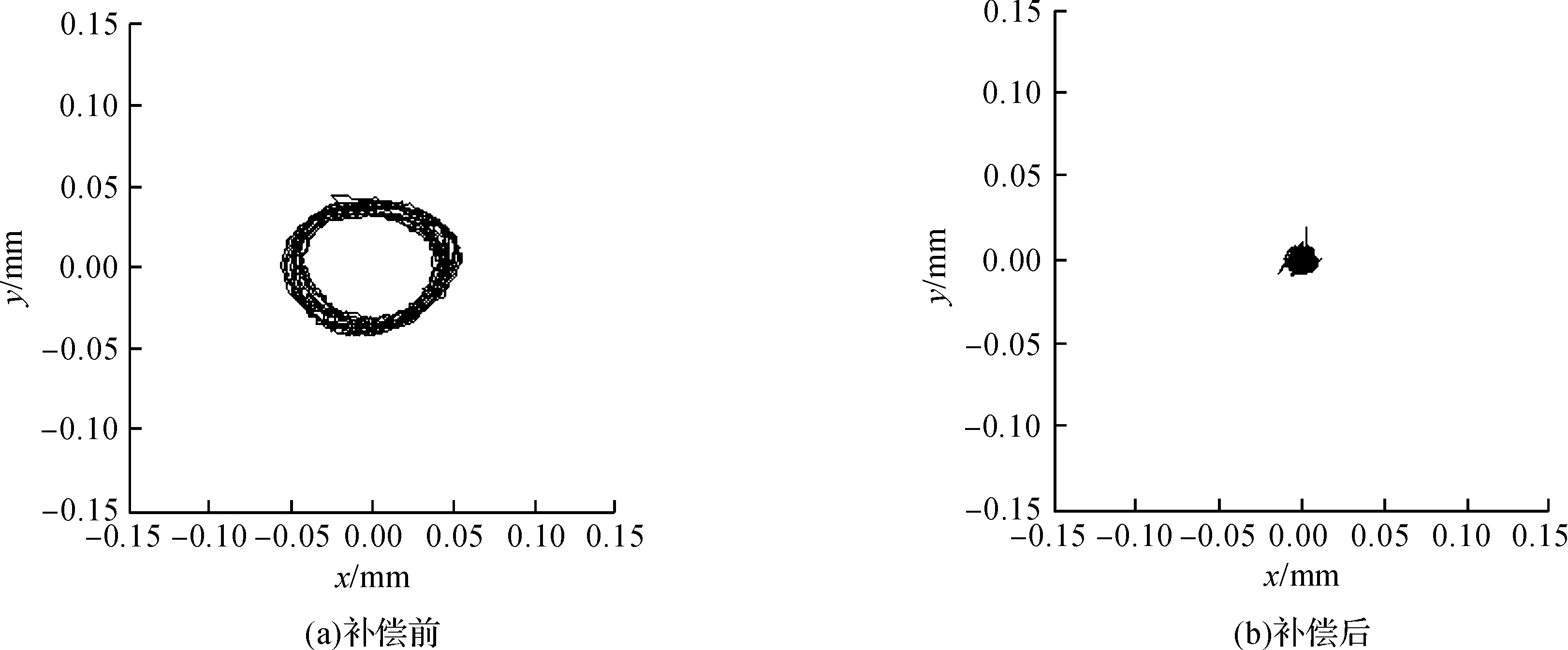
图8 不平衡补偿对转子轴心运动轨迹的影响
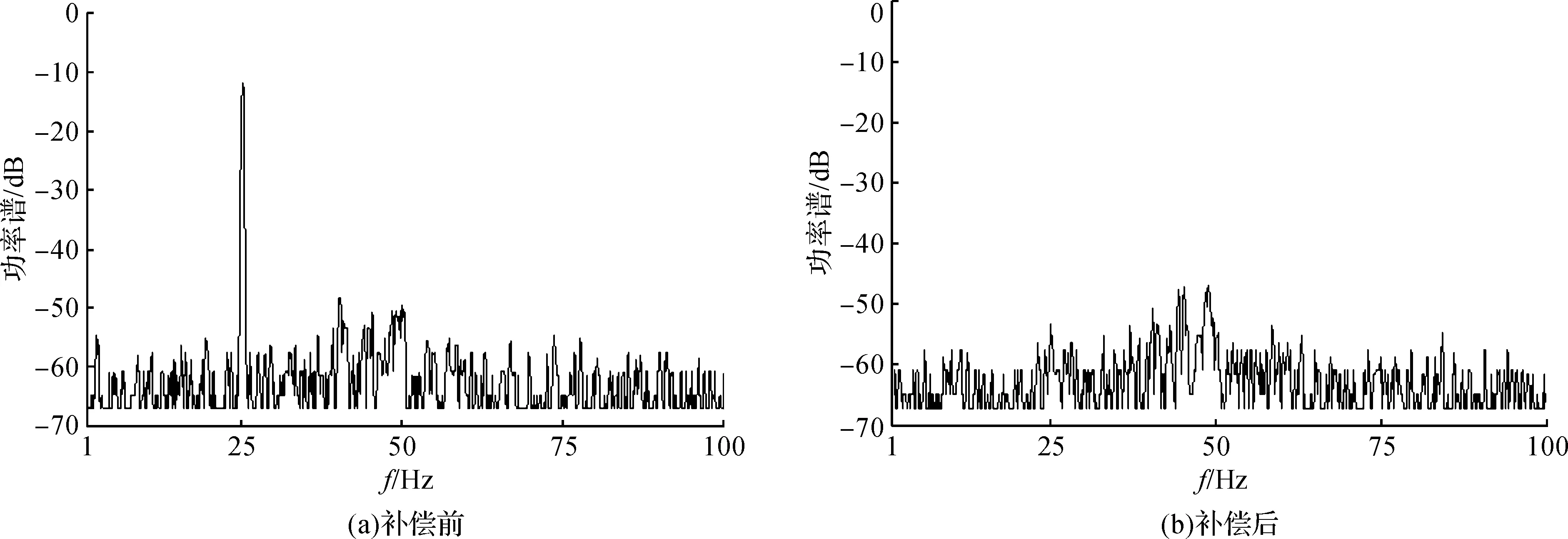
图9 不平衡补偿对振动功率谱的影响
6 结 论
本文提出了一种新的主动电磁轴承转子系统不平衡振动控制方法,该方法可以获取转子的质心轴向位置,能够对转子振动的平动和锥动进行解耦控制,通过对电磁轴承施加自适应调节的试探性补偿信号,同时检测转子两端位移响应中的平动和锥动变化,以迭代搜寻的方式产生精确的补偿信号,最终使转子的不平衡振动得到有效抑制。
在主动电磁轴承支撑的转子系统上进行实验,结果表明,本文提出的电磁轴承实现振动姿态解耦控制的方法能有效抑制转子的不平衡振动,显著提高了转子的旋转精度。
[1] Vahedforough E, Shafai B, Beale S. Estimation and rejection of unknown sinusoidal disturbances using a generalized adaptive forced balancing method[C]// Proceedings of the 2007 American Control Conference. IEEE,2007:3529-3534.
[2] Schuhmann T, Hofmann W, Werner R. Improving operational performance of active magnetic bearings using Kalman filter and state feedback control[J]. IEEE Transactions on Industrial Electronics,2012,59(2):821-829.
[3] Jiang K, Zhu C, Chen L. Unbalance compensation by recursive seeking unbalance mass position in active magnetic bearing-rotor system[J]. IEEE Transactions on Industrial Electronics,2015,62(9):5655-5664.
[4] 房建成,张会娟,刘虎.磁悬浮刚性转子系统振动机理分析与动力学建模[J].控制理论与应用,2014,31(12):1707-1713.
[5] 黄立权,王维民,苏奕儒,等.基于电磁自愈力的转子自动平衡方法与实验研究[J].振动与冲击,2011,30(1):208-212.
[6] 韩辅君,房建成.磁悬浮飞轮转子系统的现场动平衡方法[J].航空学报,2010,31(1):184-190.
[7] 蒋科坚,祝长生.主动电磁轴承转子系统自适应不平衡补偿控制[J].浙江大学学报(工学版),2011,45(3):503-509.
[8] 王秋晓,汪飞,孔波.一种改进的卫星旋转载荷动平衡的振动结构[J].振动与冲击,2016,35(3):204-208.
[9] 章琦,祝长生.电磁悬浮飞轮转子系统的模态解耦控制[J].振动工程学报,2012,25(3):302-310.
[10] 徐宾刚,屈梁生.非对称转子的全息动平衡技术[J].西安交通大学学报,2000,34(3):60-65.
[11] Shahgholi M, Khadem S E. Primary and parametric resonances of asymmetrical rotating shafts with stretching nonlinearity[J]. Mechanism and Machine,2012,51(5):131-144.
[12] Shahgholi M, Khadem S E. Internal, combinational and sub-harmonic resonances of a nonlinear asymmetrical rotating shaft[J].Nonlinear Dynamics,2014,79(1):173-184.
[13] 徐鑫莉.回转体质偏测量方法研究及精度分析[D].长春:长春理工大学,2013.
[14] 钟一谔,何衍宗,王正,等.转子动力学[M].北京:清华大学出版社,1987:207-211.

