一点五维的巴赫:巴赫与数字的随想
马慧元
一
一九七九年,一本叫作GEB(G?del, Escher, Bach: An Eternal Golden Braid,中译《哥德尔,艾舍尔,巴赫:集异璧之大成》)的奇书横空出世。作者侯世达(Douglas R. Hofstadter)自己说,“它并非意在讨论数学、音乐和艺术的关系”,“而是指出无意义的元素中怎样在自指和各种形式化规则(formal rules)中获得意义”。书中举了大量例子,比如任意的字符串如何在规则下形成语言,从无意义到有意义;阿基里斯和乌龟如何在悖论中缠绕;巴赫音乐在自指和递归中抽茧剥丝,在赋格进行中完成调性大循环,等等。
但本书还是不可避免地被当成讨论“艺术和科学的普遍形式和体系”之作。受它的影响,对巴赫与数学的讨论一时颇为兴盛,其中最时髦的话题之一就是“巴赫与分形”。
分形(fractal)这个概念,由科学家曼德博(Benoit B. Mandelbrot)创立于一九七五年,主要用于研究粗糙、不规则的几何形状,比如海岸线。近年来,它的应用遍及生物、地震、图像处理等领域。其中从视觉上更吸引普通人的一类是“自相似”的分形,也就是不断按比例缩小下去仍然类似全体的一个门类。因为它的直观、有趣和丰富的隐喻性,吸引了许多领域的人。演奏巴赫出名的美国钢琴家图蕾克对此就很有兴趣,她喜欢探寻巴赫和科学的联系,跟生物学家古尔德、物理学家彭罗斯以及创立“分形”概念的曼德博都有合作,可谓音乐家中的神奇跨界者。
在这里,只举一个分形维(dimension)计算的小小例子。平常说到维度,一般都是一维、二维、三维等等,是分形的概念引入了一种新概念下的度量。比如常见的分形谢尔平斯基三角(图1),维度值就是按比例缩小出来的小三角,需要“多少个”才能填充原先的大三角:
维度值D也就可以这样算出来,它的结果告诉我们,这个谢尔平斯基三角是1.585维的分形结构:
而在复调音乐中,有时把主题(通常几小节长)放在不同的声部中叠奏(stretto),这样主题既错开又彼此呼应;有些时候,某个声部把主题拉长或者缩短,音乐的形态有些新意却仍然熟悉。这都是古已有之的写法,巴赫将之发挥到了极致。有人把巴赫的《赋格的艺术》中的第七赋格(全曲共十四个赋格,四个卡农)按旋律线做成图(图2)。其中每个圆点是主题的一个音,而横线是主题之外的音,不同长度代表不同时值。这样一来,不同颜色的主题按不同的时值进行(跟前面提到的三角形一样,按比例放缩),有时候,不同声部之间就体现这种主题的比例,各种形态的主题平行行驶,有时相遇,最终交汇于静止,仿佛是一种抽象意义上的谢尔平斯基三角。
几十年过去之后,或许大家感到巴赫和分形的联系,以及广义上巴赫和数学的联系已经挖到了尽头,类似话题的论文和研究大为减少。毕竟,有着分形特质的音乐很多,人们随时可以写出比巴赫更有结构的音乐,但这不能表明它们是伟大的音乐。有个名叫Harlan Brothers的美国数学家兼吉他手,穷尽十年时间追索各种“分形音乐”,他认为巴赫的《勃兰登堡协奏曲》第一首以及《大提琴无伴奏组曲》第三首都有典型的分形。他自己也写了一些“分形音乐”,简直走火入魔。可是,音乐毕竟是音乐,它不可能拥有无穷的结构,更不可能像真正的分形那样,无穷放大之后仍然见微知著。一味追求音乐和科学的对应的研究者,有时会受不了诱惑,索性让算法和公式来解释音乐。上文提到的音乐家图蕾克,跟人就有过一些论争,虽然她对“音乐与分形”的话题很感兴趣,但不会接受巴赫的套路能被公式一网打尽。
不过,我认为赋格和卡农这类古老的形式,迟早有一天会与某种数学分支有所遇合,这是宿命。因为它发轫于“自相似”,以一个执着的主题牵引出无穷变体,并且高度程式化。这个主题正是GEB中那类“无意义”的元素,它几乎可以是任意的四小节,巴赫只是让它比较中性,有时是一个和弦中的几个音,易于跟自己的变身仍然形成和弦。如此这般,并不稀奇。但巴赫在这个门类中累积极多,整体性、合理性无人能出其右。而数学也好,科学也好,总是始于最基本的结构,以简单的数学表达囊括无穷的现象。发轫于极简的东西相遇并有审视之眼存在,互相启发的几率是很大的。然而短暂的交汇之后它们仍会分手。
二
巴赫的音乐和数学的联系或许有限,但它跟“数字”的联系,仍然被人无尽地挖掘。最早,是神学家和音乐学家斯门德(Friedrich Smend,1893-1980)提出来从数字入手巴赫研究,巴赫的数字都有神学隐喻云云。比如多年来研究者都有这样的共识:1、2、3之和与它们的乘积都是6(所谓完全数),所以这三个数字是最完美的。不仅是巴赫,不少同时代作曲家也写六首一组的套曲。此外,巴赫的许多作品都有这样的调性变化:B-A-C;还有14(BACH=14),41(J.S.Bach=41)等等。这些“关键词”在巴赫作品中不断出现。而数字和文化的“密码”,并非巴赫独创。古巴比伦、古希腊到后来的犹太文化中,都有一種古老的传统Gematria(希伯来语),就是这样的数字隐语或者密码传统。
近年来,瑞典学者塔特罗(Ruth Tatlow)在《巴赫的数字:写作中采用的比例及
其意义》(Bach?s Numbers: Compositional Proportion and Significance)一书中把巴赫的“数字神学”研究到无以复加。在此之前她已经写过一本Bach and the Riddle of the Number Alphabet,居然还方兴未艾。
塔特罗对巴赫音乐长度的观察很独特,她也关注“数字隐喻”,但并非重点。她的重点是“比例”,不仅注意到作品内部的比例,还包括了作品集的整体长度,比如她指出《B小调弥撒》的长度是一千四百小节,《复活节清唱剧》(Easter Oratorio)和《升天清唱剧》(Ascension Oratorio)在不执行重复的情况下也是一千四百小节。《马太受难曲》是两千八百小节;大型作品的小节数,都是十或一百的倍数等等。这些小节数,有可能是巴赫写作的时候计划的,也可能是抄谱的时候根据谱面定制的。休斯敦的巴赫协会有个播客(podcast)访谈了塔特罗,让我印象深刻的是,她说写书的初衷正是为驳斥巴赫研究中的“数字迷信”,想证明这些跟数字相关的结论都是巧合下的故作文章而已。不过在这个过程中,她发现了这些大作长度的内在比例以及正正好好的小节数,等等。这可能都是巧合吗?于是初衷大改,从证伪变成求证,不过出发点与前人不同。endprint
可是,同时保持音乐的艺术完美和数字完美实在太难了,那么巴赫会因辞害意吗(或者说,在不同需求面前如何取舍)?塔特罗的研究指出,会的。巴赫有时会做一些看上去无关紧要的改动,而原稿几乎已经完美了。在BWV1006第三乐章“加沃特”中,巴赫在开头用了反复记号而不是把最后八小节写出来—如果写出来的话,那么这段总数就是一百小节而不是九十二小节—九十二小节才正好凑成两千四这个巴赫喜欢的数。仅就小提琴帕蒂塔BWV1001、BWV1002而言,塔特罗就做出一个表格(图3),让人叹为观止。
不过,塔特罗虽然做了无尽的“数小节”的工作,她一再强调,关键之处在于巴赫想要的比例,而不是数字;除此之外,巴赫非常在意作品中各个部分的内在联系和整体性。所以她给巴赫的这类用意,取了个名字“proportional parallelism”,指的是巴赫在不同层面上体现的“平行”的隐喻性。这个比例,有时是指一部作品中各个“板块”的长度比例,有时是大型作品的总长,多数时候,是指一部作品中可以分成明显的两部分,它们的长度比。巴赫喜欢简单的1 : 1、
1 : 2、2 : 3等比例,这不难理解,除了1 : 1的对称性,1 : 2、2 : 3也对应于从毕达哥拉斯时代就开始有的对简单与和谐的相信。
说到数字、数学的起源,记得有人说数学是根植于人类本能的东西,或许,与数学相关的美感也是如此。但人在遭遇艺术的时候,大约并不会直接去感受复杂的数字,只会呼应简单的比例,在时间和空间的艺术中都如此,除非经过特定的训练。数字的“完整性”,在巴赫作品中俯拾皆是,但恐怕只有读谱并且细数的人才能感知,除此之外顶多感到段落之间的短长。对多数人的感觉来说,精确的数字是一种“难溶物质”,很难转化为听觉上的美感。然而,几百年前的建筑家同样相信“上帝视角”,相信人所看不见、听不见的东西,对上帝仍然是可感的。今人在巴赫盘根錯节的音乐面前惊叹,恐怕不容易想到在赋格的规则、听觉的美感之外,巴赫还自设了那么多屏障和捆绑,他在这些羁绊之中,居然仍能找到答案。而我们假设巴赫没有这些“数字神学”的设定,他的作品又会是什么样的呢?它们会更张狂、更丰富吗?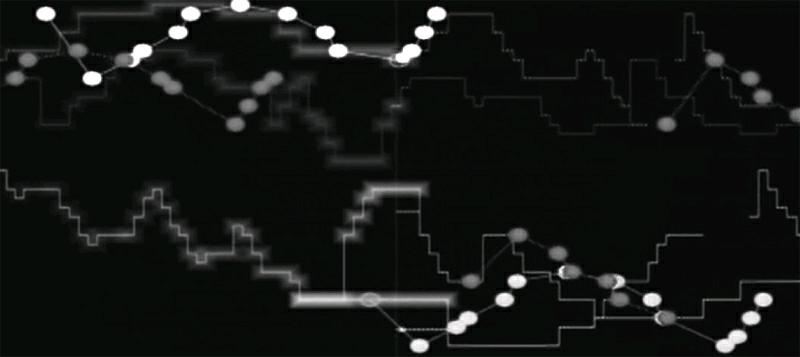
三
美国音乐学家伯格(Karol Berger)的《巴赫之环,莫扎特之箭》(Bach?s Cycle, Mozart's Arrow)一书说的不是巴赫的“另一种可能性”—虽然我私心里会歪解一下,而是不同时代中人对时间的感知方式。伯格认为,在欧洲文化中,十八世纪后半叶之后,音乐中的时间才真正成为事件线索的重要元素。
众所周知,音乐本身是有周期性的(比如音阶),它天然地需要结构,需要折返。而伯格的重点在于,因为时代和文化的不同,巴赫的音乐经常呈现出封闭的结构,它指向开端,指向自己,它常常是完美的循环—周而复始,万物皆有定时。而莫扎特这里的音乐结构已经是离弦之箭,分别、不对称已经成为主导。他列举了莫扎特钢琴协奏曲K491、歌剧《唐璜》等例子。西方音乐史上,更为明显的“离弦之箭”是贝多芬,他撕碎了圆满的结构,让音乐发生了就不再回转。伯格也在本书中讨论了贝多芬,但他认为真正的端倪是在莫扎特这里,莫扎特的音乐,已然是现代音乐。
伯格指出,巴赫的《马太受难乐》中无处不在的“返始咏叹调”(da capo aria)让结构成为环形。“没有一种时间如同上帝的时间”(There Is No Time Like Gods Time)这一章,说的就是这部受难乐既有线性的叙事结构,又有停止在瞬间的全面视角—时间在此凝固。在这里,词作者皮坎得是有自己的长度规划的,包括跟圣经相关的数字隐喻;巴赫更在乎自己的计划,尤其是音乐的长度比例,所以没有完全遵循皮坎得。
塔特罗的研究,在我读来还有些“不明觉厉”,不知道巴赫的用意跟音乐成就有没有确定的联系。不过如果对照伯格的意图和塔特罗的意图,我才有几分明白,甚至感到他们在此形成了有趣的对位—一面观测巴赫音乐的“运动”,它的“速率”“方向”“角度”;一面是巴赫的“距离”,用数字衡量的巴赫的布局。上面说过《马太受难乐》总长两千八百小节(这是1727年版,1724年版是2400小节),包括反复和da capo-da capo这个手段,对巴赫来说实在太得心应手了,它如同变速箱一般,让巴赫能凑出来各种自己想要的循环和数字比例,而事实也并非只有“凑”那么简单,巴赫把材料准备得紧密充分,一环咬一环,看上去竟是哪句都少不得,因为到处都有呼应,不能随便抽掉积木。所以,如今网上有那么多人绘出彩色的巴赫动图,它们并不是随机的万花筒图案。只是,伯格认为巴赫并不关注音乐构架的线性时间顺序,他恨不得让所有事件同时发生,透明地折叠,或者索性让“过去”和“现在”一起铺天盖地地涌来。这在《马太受难乐》中体现尤甚,视角忽远忽近,一会是耶稣身边的犹太人(歌词中以“锡安的女儿”暗指),一会又是“今人”,环环相扣对答,听者还真不容易清清楚楚地追随。在巴赫的大型作品(不仅是这部受难乐)中,环状结构无处不在,有大循环,有微循环,对称、并置比比皆是,串起它们的主要是场景的变化。
这样一来,巴赫无视事件发生的“大时间”,却对音乐进行的“小时间”也就是从段落到整体的小节数精细切割,各个段落运动活跃,转调大胆,而它们常常又是可交换和颠倒的。可是如果换个角度看,这种切割时间,让诸事件平行穿透的手法,或许更现代,普鲁斯特的巨作都能顺利地呼应它。只是,巴赫的圣马太故事毕竟是文化的一部分,它被讲述了太多次,也循环了太多次。时间没有胜利也没有失败,它睡在记忆里。
伯格所说的莫扎特的“不复返之利箭”,是时代使然。不过河西河东之后的二十世纪,巴赫看似静止的音乐又回到时风,至少回到西方古典传统之下的时风中—可是我们的时代,不是不断摒弃死板的结构吗?不错,可是我猜所谓现代又是崇尚复杂的,越来越多的工具让人破解复杂,也让人欣赏复杂—世界的狰狞真相,本来也需要复杂的艺术来映射。这个时代也有了越来越多的工具让时间静止、提速,甚至倒转。那么跟时间斗智的艺术,不会远离我们—网络游戏也好,电影也好,早让我们浸润在这样的文化之中。endprint
四
《巴赫与机器》,这是管风琴家伊尔斯利(David Yearsley)的文集《巴赫以及对位的意义》(Bach and the Meaning of Counterpoint)中的一篇。
一七四七年,法国哲学家拉·美特利(Julien Offray de La Mettrie,1709-1751)出版了轰动一时的《人是机器》(LHomme Machine),认为动物和人一样,都是机械装置,并没有“灵魂”这个东西。轩然大波之中,他从荷兰逃到弗雷德里克大帝的普鲁士。而就在一七四六年,一些有趣的新发明给拉·美特利的理论增加了佐证—德意志出现了吹长笛的机械小人,以及一只行动自如、会吃玉米粒(并且能“消化”!)的机械鸭子。这都是法国发明家瓦克桑(Jacques de Vaucanson,1709-1782)的作品,他声称这些机械音乐家能演奏二十首曲子。弗雷德里克大帝喜欢音乐,会吹长笛,他的御用长笛老师正是最杰出的长笛演奏家之一匡茨。“长笛机器人”甫一出世,匡茨老师被惊动了,他说:“无论这些机械多么精巧,它们还是不可能打動人。不过,如果人觉得自己比机器高明,并且能打动人,演奏技巧千万不能亚于它们。”可见,机器人还是威胁到了大师的存在感。
当时的莱比锡有一位波兰裔的医生,米兹勒(Lorenz Christoph Mizler,1711-1778),此人对音乐、数学都有贡献,做过巴赫的学生,还创立了一个大名鼎鼎的音乐协会。在瓦克桑发明“长笛手”的时候,米兹勒设计出一种能给音乐自动配低音的装置。因为是用算法产生和弦,它甚至发展到能写对位了,“而且迷人程度不亚于C. P. E. 巴赫(巴赫的儿子)”。既然如此,用机器产生音乐越来越可行并且好玩,很多能工巧匠兼业余乐手都开始施展身手。看来,作曲家们都要坐不住了,当时许多知识分子都在热烈争论“灵魂与机器”的问题。
说到巴赫的“机械性”,说起来大概要让许多巴赫迷恼火,包括我在内。谁也不愿承认巴赫的艺术是冰冷的公式凑出来的—如果公式化、机械化是指空洞的程式化赋格,那么巴赫的许多同时代人,包括老师、学生辈,甚至如名家布克斯特胡德,远比巴赫机械得多。可是,巴赫的音乐,让人很难忽视它跟“机械”的联系。在许许多多的对位作品中,《赋格的艺术》也好,《音乐的奉献》也好,恒河沙数的管风琴作品也好,赋格主题好像只需“第一推动”,然后就自动前行,不再需要干预,它们各自长得羽翼丰满,鬼魅一般彼此穿越。我自己在熟悉《赋格的艺术》的过程中,起先深为主题自身的孤迥之气所感,但一个个赋格、卡农听下去,直到相邻两段互为倒影的主题,就不断感叹它太“自动”、太圆熟,虽然有趣并好听,但因过于智性,离普通人的情绪有着遥远的距离。而稍稍通读《赋格的艺术》乐谱,即便不是研究者,都会注意到X小节一段的定式在卡农、对位中频频出现。比如几首对称精准、听起来又仙气袅袅的卡农。不仅主题的出现有准确的间隔,连何时出现汗漫的半音阶都有钟点般的步伐—钟点,对了,齿轮、咬合、倍数,这不都是分形的巴赫、平行的巴赫以及机器的巴赫吗?
伊尔斯利认为,巴赫是在自然的表达和“公式”之间的沟壑里探索。他对名噪一时的瓦克桑并未表达意见甚至可能并不知晓,但他近于机器般严密的卡农,也可视为十八世纪文化中对“机器艺术家”的回应。晚期所写《赋格的艺术》就是提交给音乐学会的作品,而这正是米兹勒创办的音乐协会。那个年代中的音乐批评,已经有了如此发达的科学和理论。
顺便说一下,今人用AI来作曲,据说巴赫的音乐是比较容易模仿出来的,其中做得比较好的,对许多人来说几可乱真。我对此并不惊讶,并且相信大多数巴洛克的音乐,都可以在一定程度上“AI”出来,因为样式明显,特定语汇突出,程式化极高。巴赫也同样,一些典型的样式,比如键盘作品中大量的八分音符琶音,一些赋格的答题等等,几乎在哪首曲子中都能见到一二。何况,赋格看上去太容易用算法生成了。但计算机写得出巴赫未写出的歌剧吗?写得出能和《歌德堡变奏曲》比肩的巨作吗?此为另话,目前只能存疑。
可是GEB的作者侯世达,似乎在支持巴赫的“机械性”—无生命的关联和隐喻的背后,只要有一套形式规则支持它们,就可涌现出语言、生命、认知与智能。细思恐极?
当年,巴赫在生命的末期,并不一定预知死亡,但因为最后的作品(如《赋格的艺术》)太过奇诡,又有最后一个对位未完的浪漫传说,它注定有许多种叙述方式。伊尔斯利在逐一讨论其中几首卡农之后,认为巴赫终结于一个出乎预料的“他我”。它已经独立于作曲家的存在了,它存在于自指和自我繁衍中,它像永动机,更如同一场模拟。在伊尔斯利此书写成的二○○二年,还显得颇为大胆。如今,网络上这类问题已经铺天盖地:我们的世界是不是一场模拟(simulation)?而Youtube上那些烟花般绚丽而对称的卡农动图背后,又有谁在拈花微笑?
《赋格的艺术》中十度卡农演奏过程中形成的图像(图4),较大的圆点代表不断重复出现的主题,每次出现都涂上不同的颜色。
五
当年,巴赫健康每况愈下之际,自己也知道需要节省精力,但仍然在斤斤计较作品的“比例完美”和“数字哲学”。即便在生命的最后十年中,他仍然对这种“看不见”“听不见”的完美孜孜以求,这在他的两部晚期大型作品《音乐的奉献》和《赋格的艺术》中都体现了出来。这仍然是塔特罗的研究指出的。《赋格的艺术》虽然未完,但仍大致体现了1 : 2的比例—前八个赋格总长七百九十小节,之后的部分是一千五百八十小节(塔特罗依据研究“脑补”了未写出的41小节,但数字无疑是接近的)。
只是,巴赫密集的心意从音乐辐射出去,又有几许能抵达这空疏世界的远方?
不敢说自己是接受《马太受难乐》那样大作的“天线”,只能说我一直是巴赫赋格身体力行的粉丝。曾经,《赋格的艺术》给我听觉上的冲击极大,主题一出来,有种太空般的寂静与苍凉,然而仅仅倾听已经是过去式,过去感官所触及的新奇、感官留下的热情狂想,渐渐被技术问题埋葬。现在我被主题打动的时候不那么多了,取而代之的是小心翼翼地在谱上划句子。主题从开头轮流进来的时候尚可清晰感知,之后越埋越深,甚至混搭在不同的声部中,别说一般人根本听不出来,就是看谱也未必一下子能看清,但弹琴的人必须一个个地揪出来并且心如明镜(我称之为“抓特务”)。弹赋格还有这样的难处:分句方式可以有多种,但你一旦确立自己的选择,就算许下心愿、绑上贼船,无论用哪只手还是脚,都必须严守最初的承诺,处处践行一致的分句方式(天知道有时候会别扭成什么样),才算是达到赋格的基本要求。对演奏者来说,主题散掉,丢了头尾,被周围声部淹死,都是常见事故。演奏者对待这种赋格,按说把句子咬清楚是基本要求,但做起来很难不说,也并不讨好。因为在听者那里得不到什么呼应,这不是激情表达、灵感涌现,而仅仅是维护赋格的“尊严”,让作曲家本人在场听了不会勃然大怒。endprint
此外,自己上手之前,还无知无畏地相信“《赋格的艺术》应该在羽管键琴上弹”这种话—大概最早是莱恩哈特大师说的,结论不一定错,但需要高度的上下文界定。等到自己开始弄,才发现在什么琴上弹并不要紧,反正单件乐器最终会让听者迷路。这音乐不是给人“听”的,它是供人弹奏、阅读、交流用的。你可以把声部做成上文那个彩色的动图,也可以用好几件乐器来放大它,让摩擦成一堆的声部拉開距离,从不透明但有花纹的石头变成水晶。你也可以把它切成无数小段当作标本来学习。总之,我们普通人没有上帝的视角,不能瞬间穿透它,就只能线性地在时间之中用各个方式分别打开。最终,各个侧面融会贯通,同时降临,像《马太受难乐》那样一口气泰山压顶,那时候或许好意思回头想想它“究竟属于什么乐器”。
至于音谜、字谜,我只感念巴赫和那个时代的“相信”。谜语可以留给上帝,多少代人无知无觉,多少代人无从勘破,信徒还是带着相信而死。
《赋格的艺术》有数个版本,在巴赫死后的版本中,那神秘的最后四个音“B-A-C-H”之后附了一首未完的管风琴众赞歌BWV 668,它是《十八首莱比锡众赞歌》的一部分,不少学者相信这才是真正的巴赫临终之作。《十八首》中的前十五首是巴赫自己收集的,塔特罗指出它们的总长为一千二百小节,这是巴赫在晚年不断修改编订的结果。而最后三首是他的学生兼女婿Johann Altnickol后来所抄录,终于打破了巴赫计划得好好的总小节数和长度比例。而伊尔斯利把这首题为《我来到主的宝座前》的BWV 668称为巴赫的“死亡的艺术”,更有意味的是,GEB的作者侯世达称巴赫未完之赋格(指《赋格的艺术》中“B-A-C-H”音符含巴赫名字的“自指”),好比哥德尔不完备定理中的悖论(尤其在系统包含自指的时候):“我不能被这个系统所证明。”
参考文献:
1. Bach's Numbers: Compositional Proportion and Significance, by Ruth Tatlow, Cambridge Press, 2016
2. Bach's Cycle, Mozart's Arrow: An Essay on the Origins of Musical Modernity, by Karol Berger, University of California Press, 2007
3. Bach and the Meanings of Counterpoint, by David Yearsley, Cambridge University Press, 2002endprint

