用好统计数据,做出合理估计
颜艳
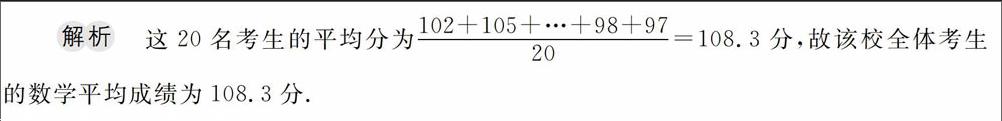

同学们,我们在抽取出样本,得到一组统计数据之后,如何科学、全面、合理地进行分析,进而估计出总体的情况呢?接下来,我们通过一组实例加以理解,
例1 从某校全体高考考生中任意抽取20名考生,其数学成绩(总分1 50分)分别为102 ,105 ,131,95 ,83 ,121, 140 ,100, 97, 96, 95, 121,124, 135, 106, 109, 110, 101, 98, 97,试估计该校全体考生的数学平均成绩.
解析 这20名考生的平均分为(102+105+···+98+97)/20=108.3分,故该校全体考生的数学平均成绩为108.3分.
总结 我们知道,样本数据的平均数刻画了数据的平均水平,所以我们可以通过计算平均数来估计总体的平均水平.
例2 王明是一家快餐店的经理,下面是该快餐店所有工作人员8月份的工资袁:(1)计算所有人8月份的平均工资;(2)计算出的平均工资能反映工作人员这个月收入的一般水平吗?
解析 (1)平均T资x=(30000+4500+3500+4000+3200+3200+4100)÷7=7500(元);
(2)由(1)所得的平均T资不能反映T作人员这个月的收入水平,这是因为王明的T资值为异常值.
总结 平均数很容易受到极端数据的影响,那些越“离群”的数据对平均数的影响很大,因此通常先剔除一些异常值之后,再计算平均数.这也是在体育、文艺等比赛中常采用“去掉一个最高分,去掉一个最低分”后再计算平均分的原因.
例3 从甲、乙两种玉米苗中各抽10株,分别测得它们的株高(单位:cm)如下:
甲:25 41 40 37 22 14 1 9 39 21 42
乙:27 1 6 44 27 44 1 6 40 40 16 40
問:(1)哪种玉米的苗长得高?(2)哪种玉米的苗长得齐?
解析 (1)计算得x甲=30,x乙一31,x甲
(2)计算得s甲2=104.2,s乙2=128.8,s甲2
总结 平均数反映了样本数据的平均水平,定量地反映了数据的集中趋势;而方差反映数据的稳定性,方差越接近0,说明稳定性越好,
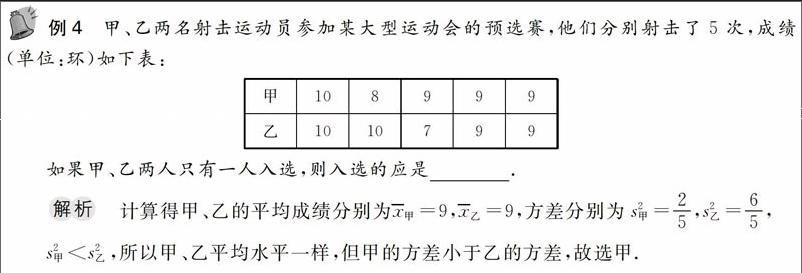
例4甲、乙两名射击运动员参加某大型运动会的预选赛,他们分别射击了5次,成绩(单位:环)如下表:如果甲、乙两人只有一人入选,则入选的应是解析 计算得甲、乙的平均成绩分别为x甲=9,x乙=9,方差分别为s甲2=2/5,s乙2=6/5,Ss甲2
解析 (答案不唯一)
1.乙品种棉花的纤维平均长度大于甲品种棉花的纤维平均长度(或:乙品种棉花的纤维长度普遍大于甲品种棉花的纤维长度);
2.甲品种棉花的纤维长度较乙品种棉花的纤维长度更分散(或:乙品种棉花的纤维长度较甲品种槁花的纤维长度更集中);
3.甲品种棉花的纤维长度的中位数为307 mm,乙品种棉花的纤维长度的中位数为318 mm.
总结 对于抽取出的样本数据,我们有时需要从平均数、方差、标准差、中位数、众数、最大值、最小值等方面分析,只有这样才能更加全面地把握数据,进而估计出总体情况.
由此可见,我们从总体中抽ILl_:样本之后,要想科学、全面、合理地进行样本数据的分析,得结合平均数、方差、中位数、众数等多方面综合考虑才行,绝对不能只看其中一个方面.

