微电网脆弱性预评估方法
周 磊,吴 辉,嵇文路,陈文君,陈美璇,刘皓明
(1.国电南瑞科技股份有限公司,南京 211000;2.国网江苏省电力公司 南京供电公司,南京 210019;3.河海大学 能源与电气学院,南京 210098)
自愈是微电网的主要特点之一,良好的自愈性能离不开科学准确的脆弱性量化评估。根据负荷预测以及微电源出力预测,考虑检修计划以及运行计划的改变,以及微电网拓扑结构变化引起的继电保护再整定等,对微电网未来时刻的脆弱性进行预评估,有利于微电网的优化运行调度和预防控制。同时,操作人员可以根据预评估结果找出系统薄弱环节,对微电网提前进行运行策略和网架结构调整,使系统更安全可靠地运行,为实现微电网自愈提供技术理论支撑[1]。
目前脆弱性评估方法主要适用于复杂的大电网,而引起微电网脆弱的因素与大电网脆弱源存在诸多差异,有系统内部设备自身的问题,也有外界扰动引发的问题。综合考虑,这些影响因素主要包括如分布式风电和光伏等微电源功率的不确定性、负荷的随机性、微电网网络结构的随机性、微电网中保护和设备故障的不确定性、自然灾害的因素以及一些偶然的人为因素等[2]。
电力系统安全评估方法基本适用于微电网脆弱性评估,已有的安全评估方法主要包括确定性方法和概率性方法。确定性方法是假定系统可能发生的故障,在每个故障情况下分析系统是否出现运行条件的越限,如N-1静态安全分析等[3]。微电网中含有大量出力不确定的微电源,如分布式风电和光伏等,因此,在微电网中更适合采用概率性方法进行脆弱性评估。概率性方法综合分析不确定性事件发生的概率以及该事件发生后造成的后果等,计及微电网中的各种不确定性因素。基于风险理论的评估方法[4—5]和基于蒙特卡罗模拟的评估方法[6]都属于概率性方法。
本文提出基于风险理论的微电网脆弱性预评估方法。首先将微电网视为存在潜在风险的脆弱系统,对其脆弱性进行定义,其次根据微电网脆弱因素发生的概率及造成的后果严重度,提出脆弱性预评估指标集,包括发电容量充裕度和供电脆弱性两大类指标,然后结合微电网中各单元特性,建立微电网预评估三相时序概率模型,进行概率潮流计算,最后结合算例实现微电网脆弱性整体评估。
1 微电网脆弱性定义
本文将微电网脆弱性定义为由于微电网内部元件对于系统内外扰动的敏感性以及缺乏应对能力而使微电网的结构和功能容易发生改变的一种内部固有属性,在系统外部扰动与内部相互作用下驱动系统内部特征而使系统的脆弱性发生变化,最终通过系统应对扰动的脆弱性以及应对能力来体现。
风险即为不确定性对目标的影响,根据微电网特性,风险理论作为将风险发生可能性和造成风险后果的严重度相结合的理论,能够较为完整的反映系统脆弱源的综合影响。一般将风险值定义为事件发生的可能性与相应后果的乘积

式中:u为各种风险;P(u)为风险发生的概率;S(u)为风险后果的严重度;R为各个风险可能造成的综合损失,通常系统越坚强风险损失越小。
2 微电网脆弱性预评估指标体系
本文建立的预评估指标体系包含发电容量充裕度(generation capacity adequacy)和系统供电脆弱性(power supply vulnerability)2个部分。
2.1 发电容量充裕度
发电容量充裕度[7]是指微电网在计及系统运行计划、元件支路不过载、母线电压和系统频率维持在允许范围的前提下,满足用户需求和电量的能力。同时,在用电高峰、某一机组检修或因故障停运等情况下也能满足电能需求。
发电容量充裕度分析需要充分考虑一些时变因素,如微电源出力、负荷水平、机组检修,运行计划和故障等。由于在微电网中存在着大量的光伏和风电这些发电设备,其出力是不确定和不可控的,具有时变性,因此在微电网未来运行态预评估中需要根据负荷和电源功率预测来获得某指定时刻的发电容量充裕度。
传统电力系统容量充裕度指标主要有失负荷概率(loss of load probability,LOLP)、失负荷频率(loss of load frequency,LOLF)和电量不足期望(expected energy not served,EENS)等[8]。这些指标多为针对一段时间内的系统运行状态,而本文的脆弱性是预测未来某一时刻微电网的安全可靠性,因而传统指标不适用于本文。为此,本文定义微电网未来某时刻t发电容量充裕度的概念为

式中:PG(t)为微电网可用发电功率之和;PL(t)为总负荷。
当微电网处于孤岛运行状态时,PG()t为微电网中所有分布式发电功率和储能放电功率之和;当微电网处于联网运行状态时,还应包括配电网所能提供的最大功率。
2.2 系统供电脆弱性
微电网运行状态受多种内在或者外在因素影响,可能会引起过负荷、电压越界、低功率因数、三相不平衡等不正常运行状态,严重时甚至可能失去部分或全部负荷。因此微电网供电脆弱性考虑如下5类风险指标,用以量化度量未来某时刻微电网运行状态。
2.2.1 失负荷风险
微电网中由于外力干扰、元件故障、继电保护的误动或拒动等风险源引起的脆弱后果都可以通过失负荷量的大小来衡量。失负荷风险反映的是系统承受扰动后发生失负荷风险的可能性和由此产生的风险后果。
(1)外力干扰
强外力干扰是造成微电网中微电源、母线、支路等设备发生严重故障的外界扰动因素。通常自然灾害的可能性低于人为破坏,所以本文主要讨论外界人为破坏。设微电网遭受人为破坏的概率服从参数为λr的泊松分布,则在t时刻,微电网遭受外界人为干扰的可能性为

(2)元件故障
微电网中含有各种分布式微电源、变压器、母线和支路等元件,每个元件都有发生故障的可能,停电事故往往都是由元件故障和系统中的薄弱环节共同作用而造成的连锁反应,所以需要考虑元件故障因素的风险评估。
系统元件的故障原因大致可分为早期故障、偶然故障及老化失效3种,它们的故障率特性如图1所示。

图1 不同使用时期元件故障率
早期故障一般会在投入运行前排除,故主要考虑偶然故障和老化失效[9]。偶然故障和老化失效服从不同参数的分布函数。
非外力干扰引起的偶然故障事件往往是相互独立的,在t时刻,其发生偶然故障的概率是常数,故障概率是服从参数为λe的指数分布

对于老化故障,其故障概率服从参数为α和β的威布尔分布[9]

假设老化元件数占总元件数的比例为η( )
0<η<1,则单位时间内元件的混合故障概率为

(3)继电保护拒动和误动
当系统发生异常时,继电保护可能会发生拒动的风险,因此继电保护拒动为一个条件概率,其拒动概率为

式中:Pj(t)为继电保护发生拒动的统计概率;为系统故障概率[2]。
(4)系统综合失负荷概率
综上,在t时刻系统失负荷的概率为

设失负荷严重度函数为SLL。相较于其他风险,发生失负荷的严重度等级最高,故一旦发生失负荷事件,直接定义其严重度为1,即SLL=1。
则未来某时刻t,系统总的失负荷风险指标可表示为
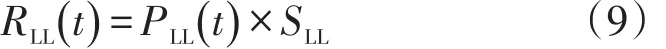
2.2.2 过负荷风险
在微电网中,过负荷是指流过发电机、变压器或线路的电流超过额定电流或规定的允许值。过负荷风险反映的是系统在正常运行或承受扰动时,线路或者变压器上功率发生过载的可能性与由此产生的后果。
定义过负荷风险严重度函数为SOL(I),I为流过支路的电流期望值与额定电流的比值,IN表示支路过负荷的阈值。对于变压器支路,由于每台变压器都很重要,且各自重要度不一样,设严重度函数中每台变压器的权重系数为KT,一般支路权重系数则取为1。则过负荷风险严重度函数为
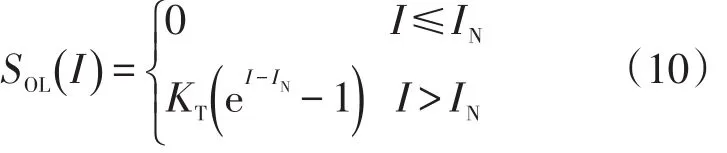
故未来某时刻t支路总过负荷风险ROL(t)为

式中:Nb为微电网中总支路数。
2.2.3 过电压风险
假设节点电压标幺值的限值为Umin、Umax和U′min、U′max。其中,U′min和U′max是系统中各节点电压继电保护装置的整定值,Umin和Umax是运行规程要求的电压运行上下限。当Ui∉[ ]U′min,U′max时,继电保护动作,故障切除,引起的失负荷已经在失负荷风险中计及;当时,电压满足要求,不存在过电压风险;其余情况下,则存在过电压风险,定义电压偏移量[1]为

定义母线过电压风险严重度函数为SV(ΔU)。若微电网中各节点的重要程度有所不同,可设置节点电压越限的风险权重系数KV,则定义节点电压越限的严重度函数为
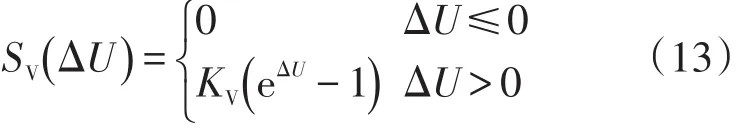
则未来某时刻t微电网整体过电压风险为

式中:PVi(t)为未来某时刻t节点i的过电压统计概率;N为电网中总的节点数。
2.2.4 低功率因数风险
微电网中存在大量的电力电子器件,并且存在一些无功负荷,导致系统负荷功率因数较低,进一步影响微电网的网损及供电质量。负荷低功率因数脆弱性指标反映的功率因数下降发生的概率以及风险后果严重度。
设低负荷功率因数的严重度函数为Sλ(λ),设置功率因数的阈值为λm,由于系统中每个负荷的重要度不一样,可设置低功率因数风险权重系数为Kλ,则严重度函数可表示为

则未来某时刻t总低负荷功率因数风险指标为

式中:Pλi()t为未来某时刻t节点i发生低功率因数的统计概率。
2.2.5 三相不平衡风险
正常运行时,微电网的三相不平衡现象是由三相系统的阻抗参数或三相负荷不对称引起的[10]。低压微电网以三相四线制形式进行输配电,如果系统发生如缺相、单相接地电阻接地等故障时则会出现三相严重不平衡。三相电压不均衡度和电流不均衡度可定义为

设三相不平衡的严重度函数为Sε(ε),每个三相支路的重要度不一样,设风险后果的权重系数为Kε,则定义三相不平衡的严重度函数为

式中:ε由概率潮流计算的三相电压或电流的期望值得到,这里可以取ε=εI;Kε为三相不平衡支路的权重系数。
则未来某时刻t总的三相不平衡风险指标为

式中:Pεi()t为未来某时刻t第i条支路发生三相不平衡的概率。
3 微电网脆弱性预评估流程
建立微电网脆弱性预评估指标体系后,对微电网进行脆弱性预评估,具体流程如图2所示。
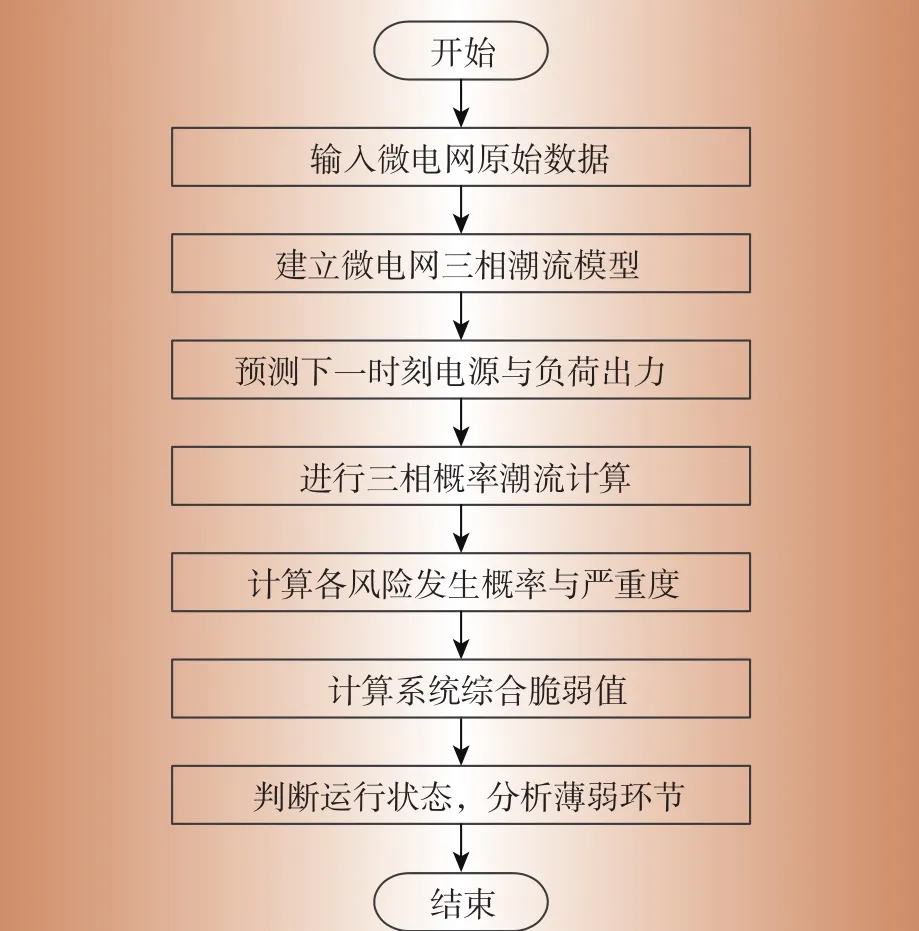
图2 脆弱性评估流程
(1)输入微电网原始数据,主要包括微电网连网或孤岛运行状态、三相模型参数,如微电源、负荷、变压器三相功率、线路三相阻抗等,建立微电网三相潮流模型[11]。
(2)基于数值气象预报和合适的预测方法对微电网未来某时刻的功率进行预测(例如未来5 min),包括微电网负荷以及光伏[12]、风电出力的预测[13]。
(3)进行概率潮流计算,本文采用基于不动点迭代的分相潮流计算方法,通过蒙特卡罗计算微电网三相概率潮流[14—16]。
(4)通过统计分析,获得微电网潮流的概率分布特性,计算各风险指标发生的概率和严重度。
(5)计算系统综合脆弱值,根据系统各节点、支路的重要程度,设置不同权值,计算出各类指标综合值。
(6)判断系统当前状态是正常运行状态、设备检修或预想故障状态;结合实际运行状态,可进一步诊断脆弱值综合评估结果所反映出的微电网真实状态和薄弱环节。
4 算例分析
本文采用33节点算例,如图3所示。节点1为与配电网连接的PCC节点,但此时联络开关断开,微电网处于孤岛运行模式。支路20—21缺相运行,支路21—22单相运行。算例中参数取值:系统参考电压VB=12.66 kV ,Umin=0.95,Umax=1.05,U′min=0.85,U′max=1.15,λr=0.003,λe=0.002,α=0.106 4,β=2,η=0.32。

图3 33节点微电网
为模拟微电网中微电源,在33节点算例中接入分布式电源,包括分布式光伏和风力发电,如表1所示。其中,节点6除接入光伏1之外,还配置额定容量为300 kW的微型燃气轮机作为备用电源。

表1 微电源分布
(1)发电容量充裕度预评估
考虑正常运行、光伏风电分别停运5种情况下,中午某时刻的系统充裕度,计算结果如表2所示。
由表2可以看出,光伏停运对系统充裕度的影响较大。因此中午时刻,相同配置容量的分布式光伏和风力发电相比,光伏出力较大,停运时的发电损失较大。事实上,若假设此时2个分布式光伏全部停运,则微电网发电容量充裕度仅为0.063 2。考虑可控有功功率源的影响,若此时不计及微型燃气轮机,则任何光伏停运将导致微电网发电容量充裕度为负。可控有功功率源的容量越大,输出的功率越大,系统的发电容量充裕度越大,可大大减少分布式光伏或风电对微电网整体发电充裕度的影响。

表2 多种因素干扰下的发电容量充裕度
(2)系统供电脆弱性预评估
根据影响脆弱性预评估的因素,分3种情况对微电网进行脆弱性预评估。
情况1:正常运行;
情况2:光伏1停运;
情况3:光伏1停运,启用微型燃气轮机供电;
采用本文提出的风险指标计算方法分别评估3种情况下的系统供电脆弱值,如表3所示。

表3 系统供电脆弱性综合评估值
由表3可以看出,光伏1停运时,系统的支路过负荷和电压越限风险较正常运行时明显增大,但系统的失负荷风险、低功率因数风险和三相不平衡风险受到的影响不大。光伏1停运时使用微型燃气轮机继续供电,基本能够完全弥补光伏1停运对各项供电脆弱性指标的影响。这说明若微电网中配置了可控有功电源,可使系统整体脆弱性降低。
5 结论
本文提出了基于概率风险理论的微电网脆弱性预评估的方法。首先给出了微电网的脆弱性定义;其次建立了脆弱性预评估的指标集,包括发电容量充裕度和供电脆弱性2类指标,接着给出微电网脆弱性预评估流程,并通过算例验证评估算法的有效性。通过本文所提的脆弱性预评估方法,能够根据评估结果分析微电网的脆弱程度,找出微电网运行的薄弱环节,掌握微电网未来时刻的状态变化,这对优化微电网结构、实现可控电源的控制、制定检修计划等均能提供有效的支撑。D
[1] 刘皓明,黄春燕,陈懿.基于风险理论的微电网脆弱性评估[J].电力系统及其自动化学报,2014,26(10):1-7.
[2] 刘皓明,袁小慧,张泽宇,等.低压微电网运行脆弱性评估.电力需求侧管理,2017,19(2):14-19.
[3] 彭寒梅,曹一家,黄小庆.对等控制孤岛微电网的静态安全风险评估[J].中国电机工程学报,2016,36(18):4837-4846.
[4] Preece,R.Milanovic,J.V.Risk Based Small Disturbance SecurityAssessmentofPowerSystems [J].IEEE Transactions on Power Delivery,2015,30(2):590-598.
[5] Xingbin Yu,Chanan Singh.A practical approach for integrated powersystem vulnerability analysiswith protection failures[J].IEEE Transactions on Power Systems,2004,19(4):1 811-1 820.
[6] Rei,A.M.,Schilling,M.T.,Reliability Assessment of the Brazilian Power System Using Enumeration and Monte Carlo[J].IEEE Transactions on Power System,2008,23(3):1 480-1 487.
[7] Billinton,R.;Bagen.A sequential simulation method for the generating capacity adequacy evaluation of small stand-alone wind energy conversion systems[C]//IEEE CanadianConferenceElectricalandComputerEngineering,2002:72-77.
[8] 栗文义,张保会,巴根.风/柴/储能系统发电容量充裕度评估[J].中国电机工程学报,2006,26(16):62-67.
[9] Li W.Incorporating aging failures in power system reliability evaluation[J].IEEE Trans on Power System.2002,17(3):918-923.
[10] Tanabe,T.,Funabashi,T.,Nara,K.,et al.A loss minimum re-configuration algorithm of distribution systems under three-phase unbalanced condition[C]//Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century,2008:1-4.
[11] Haoming Liu,Shun’an Cheng,Chunyan Huang,et al.Unbalanced Power Flow Calculation for Low-voltage Distribution Systems Including DGs[C]//IEEE PES Innovative Smart Grid Technologies,2012:1-5.
[12] Lei Zhou,Hui Wu,Tao Xu,et al.Ultra-Short Term Hybrid Power Forecasting Model for Photovoltaic Power Station with Meteorological Monitoring Data [C]//The 32nd Youth Academic AnnualConference ofChinese AssociationofAutomation,2017:452-456.
[13] Li Jinxuan,Mao Jiandong.Ultra-short-term wind power prediction using BP neural network[C]//2014 IEEE 9th Conference on Industrial Electronics and Applications,2014:2 001-2 006.
[14] 黄春燕,刘皓明,钱程晨.低压微电网概率潮流计算[J].电力需求侧管理,2013,15(2):11-15.
[15] 岳付昌,王博,杜云虎,等.离网型海岛综合能源微电网架构设计与实现[J].江苏电机工程,2016,35(5):44-47,52.
[16] 王辉.计及孤岛约束的微网经济优化[J].江苏电机工程,2016,35(5):57-62.

