通过求解加速度问题进行动力学的研究分析
王晓云,陈 堃,李 梦
(安徽信息工程学院 机械工程系,安徽 芜湖 241000)
《理论力学》是研究物体机械运动,一般规律的一门学科[1],包括静力学运动学和动力学三部分内容,其中动力学是研究物体机械运动与作用力之间的关系,包括了静力学和运动学研究内容,是两者之间的有机结合.在课堂教学中,学生对动力学内容理解不够透彻,掌握不够扎实,达不到预期的教学目的.究其原因,主要有以下三点,一是研究对象不清晰,动力学内容的主要内容的主要研究对象是刚体,是不变质点系,学生通常将物理中对于质点的研究方法套用在刚体上,造成方法使用错误,二是动力学内容多,学时紧.动力学包括动力学普遍定理,虚位移原理、达朗贝尔原理、碰撞和拉格朗日方程的内容,通常只有20多个学时.导致学生对内容掌握不牢固;三是内容难、学生理解不透彻,动力学问题与实践联系紧密,涉及内容多,需要具有一定的逻辑分析能力,如果前期学习基础不够扎实,对这部分内容的理解会造成很大的困难.
针对以上问题,笔者结合自身教学经验,通过对一道题求解加速度的众多方法,悉数动力学主要研究方法,加深学生对动力学内容的理解,力求达到举一反三.
1 具体实例分析
一辆简易平板车如图1.杆的质量是m;两圆柱体质量分别为m/2,半径为r;设接触处都有摩擦,无相对滑动.求当杆上加水平力P时,求杆的加速度.

图1 简易平板车
方法一:应用动能定理求导
研究对象去整体,设杆向右移动距离为x,受力及运动分析如图2.

图2 受力及运动分析
主动力的功∑W(F)=Px写出两个状态的动能,设初状态的动能T0,由上知,任意时刻动能T=mv2代入动能定理T-T0=∑W(F),即mv2-T0=Px,
该方法适用于单自由度,系统所含物体较多,约束力复杂的情况,需要注意,利用该方法求解加速度时,系统的动能和功具有一般特性,以便等式两边可以同时求导.
方法二:直接应用动能定理
研究对象取整体,设杆向右移动距离x,
根据主动力的功,写出两个状态的动能,设初状态的动能T0,速度为v0,由上知,任意时刻动能T=mv2.
则,T0=
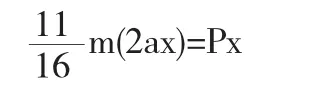
该方法与方法一适用范围类似,可以求解速度又可以求解加速度,由于借助运动学关系,补充了两时刻速度与加速度之间的关系,在问题求解时,可以省略求导这一步,使得运算更加便捷.
方法三:功率方程
研究对象取整体,设杆在拉力P作用下具有向右的速度v,主动力的功率∑P(F)=Pv,且由上易知,将任意时刻动能代入功率方程
该方法利用功率方程能够快速有效求解加速度,但如果对速度进行分析,需要进一步对加速度进行积分.
方法四:应用动量定理与动量矩定理
先研究杆,受力及运动分析如图3所示,
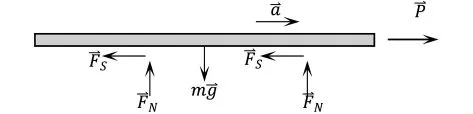
图3 杆的受力及运动分析
水平方向应用质心运动定理,可以得到ma=P-2FS再研究圆柱体,受力及运动分析如图4所示.

图4 圆柱体的受力及运动分析
对P点应用顶轴转动微分方程JPα=F'S·2r,其中α=a=2aC
该方法是一种通用的方法,其核心是平面运动微分方程,具有思路清晰,方法简洁的特点.然而在求解过程中需要先对系统中各物体进行受力和运动分析,对于复杂系统而言,由于约束力的性质和分布在求解前是不易确定的,使得求解过程变得极为复杂.
方法五:达朗贝尔原理
先研究杆,受力及运动分析如图5所示:

图5 杆的受力和运动分析
沿水平方向列平衡方程,可以得到P-2FS-FI杆=0
再研究圆柱体,受力及运动分析如图4所示.
以P为矩形,列出矩方程,-F'S·2r+FIr+MIC=0,其中,α=
该方法与方法四类似,也是一种通用的方法,然而较方法四,矩方程更为灵活,矩方程的矩心不受任何限制,是次此方法的主要优势.
方法六:应用拉格朗日方程
取系统为研究对象,此系统具有一定的自由度,选杆的水平位移x为广义坐标,如图6所示.

图6 广义坐标
计算广义力(虚功法):Qx
∑δW(F)=Pδx,则,Qx=P
计算动能:设任一瞬时,杆的平移速度为v,圆柱体纯滚动,角速度

由此得:

该方法利用系统能量,建立拉格朗日方程,使得问题的分析变得清晰明了,特别是系统的约束力未知,自由度较多时,优势尤为明显.
3 结束语
本文以一道常见例题为对象,利用六种方法进行了分析求解,分别应用了质心运动定理,动量矩定理、功能定理、功率方程、达朗贝尔原理和拉格朗日方程等多种方法,几乎涵盖了全部的动力学内容,力求达到动力学内容的融会贯通,希望能够增强学生对这些定理的理解,能够正确使用这些定理解决实际问题,从而达到动力学的基本目的.
〔1〕哈尔滨工业大学理论力学教研室.理论力学I、II(第7版)[M].北京:高等教育出版社,2009.

