调和Dirichlet空间上以径向函数为符号的Toeplitz算子的交换性

杨静宇

（赤峰学院 数学与统计学院，内蒙古 赤峰 024000）

1 引言

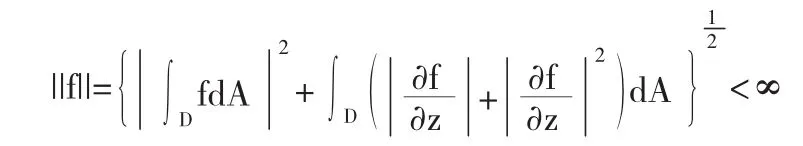
进一步S按下述内积成为Hilbert空间

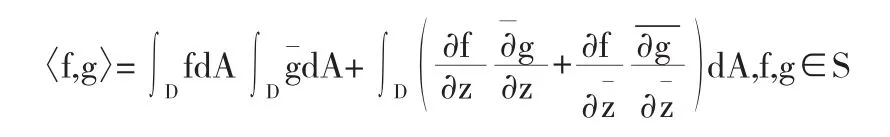
Dirichlet空间W是S中满足f(0)=0的解析函数全体构成的S的闭子空间，是一个再生Hilbert空间，再生核是

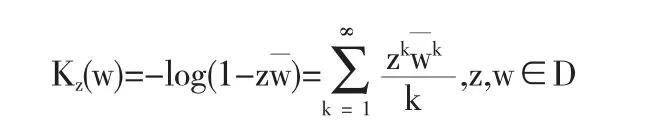
调和Dirichlet空间Wh是S中的调和函数全体所成的闭子空间，很容易得出

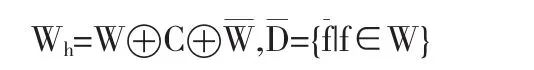
并且调和Dirichlet空间Wh也是一个再生Hilbert空间，再生核是

设Q表示S到Wh上的正交投影，那么

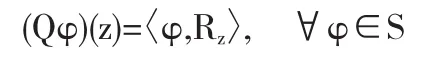
同理，若P表示S到W上的正交投影，那么

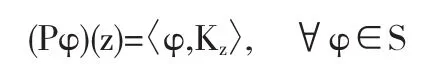
由（1.1）式，有

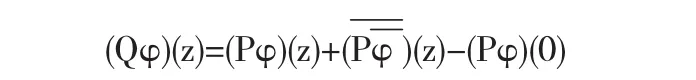
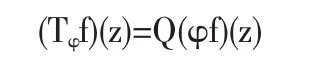
其中 f∈Wh,z∈D.

1964年，Brown和Halmos[1]对Hardy空间上以有界函数为符号的两个Toeplitz算子Tψ和Tφ的交换性给出一个漂亮的充分必要条件：（1）ψ和φ都解析；（2）ψ和φ都余解析；（3）存在不全为零的常数 α,β，使得 ψ=αφ+β.在 Bergman 空间上，第一个关于Toeplitz算子交换性的结果由Axler和Cukovic[2]给出.在[2]中他们证明了当两个符号函数是有界调和函数时，关于Toeplitz算子的交换性仍有Brown-Halmos型结论.Louhichi和Zakariasy在[3]中讨论了以拟奇次函数为符号的Toeplitz算子的交换性.

由于两个调和函数的乘积不一定是调和函数，使得调和函数空间上相关算子的研究变得异常复杂和困难.文[4]在调和Bergman空间刻画了符号为调和函数且其中一个为多项式的两个Toeplitz算子的交换性.特别的，文中证明了只有符号函数线性相关的两个解析Toeplitz算子才是交换的，但在Bergman空间上两个解析Toeplitz算子本身就是交换的.文 [5]刻画了调和Dirichlet空间中以调和函数为符号的Toeplitz算子的交换性.

受文献[3],[4],[5]的启发，本文考察了调和Dirichlet空间上以径向函数为符号的两个Toeplitz算子的交换性.

2 主要引理

设 φ∈W1,∞是径向函数定为：

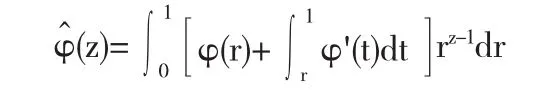
若 φ∈L1(D,dA)且满足 φ(z)=φ(|z|)(∀z∈D)，则称 φ 为径向函数.函数f称为度为k的拟奇次函数，如果f能表示为

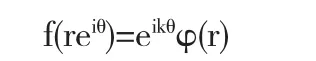
其中φ为径向函数.

引理1设φ∈W1,∞是一个径向函数，那么对任意的p,n∈N∪{0},有

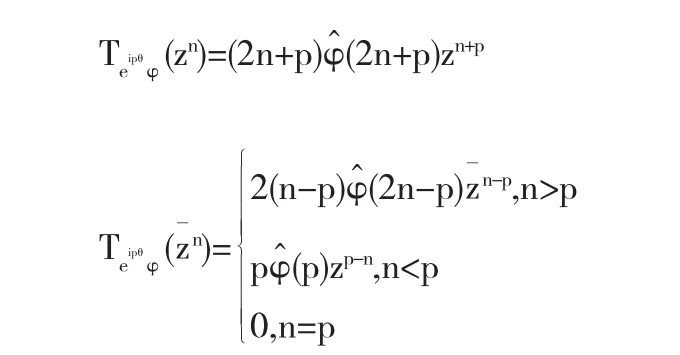
证明以为例

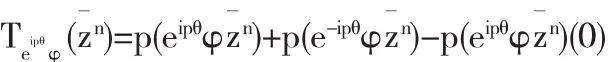
进一步的

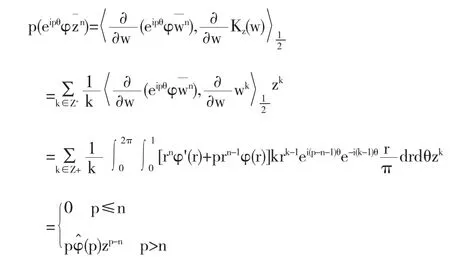
同样的方法可得

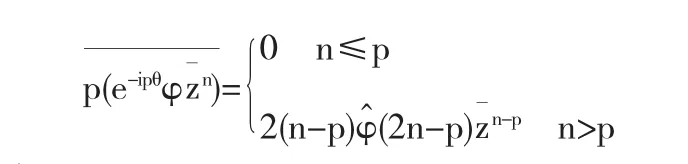
综上可得

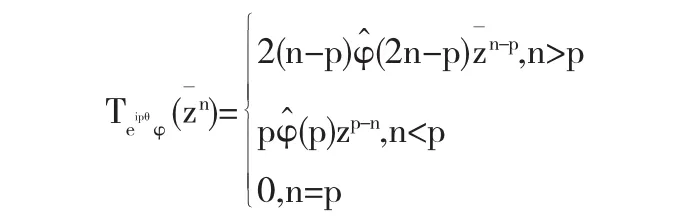
3 Toeplitz算子的交换性

定理 1设 φ,ø∈W1,∞是径向函数，那么 TφTø=TøTφ.

证明由于φ,ø∈W1,∞是径向函数，根源引理1有

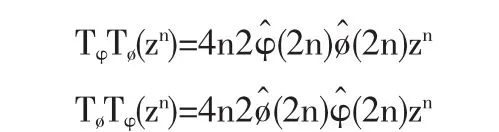
所以

同理可得

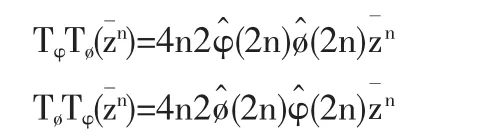
有

由等式（2）（3）可以推出在 Wh上 TφTø=TøTφ.

〔1〕A.Brown and P.R.Halmos,Algebraic properties of Toeplitz operators,J.Reine Angew.Math.213,(1963),89-102.

〔2〕S.Axler and Z. Cuckovic,Commuting Toeplitz operators with harmonic symbols.IntegralEquation Operator Theory.14,(1991),1—12.

〔3〕I.Louhichi and L.Zakariasy,On Toeplitz operators withquasihomogeneous symbols,Arch.Math.(Basel).85,(2005),248-257.

〔4〕B.R.Choeand Y.J.Lee,Commuting Toeplitz operators on the harmonic Bergman space,Michigan Math.J.46,(1999),163-174.

〔5〕L.Zhao,Commutativity of Toeplitz operators on the harmonic Dirichlet space,J.Math.Anal.Appl. 339(2008),1148-1160.