坦克多体系统动力学建模及模型试验验证
郝丙飞 王红岩 芮 强 王钦龙
陆军装甲兵学院工程车辆运用系,北京,100072
0 引言
多体动力学建模及仿真是当前研究坦克行驶平顺性、操纵稳定性和越野机动性的一种非常重要的手段[1-2]。
居乃鵕[3]根据坦克的垂向振动特性,忽略履带对车体振动的影响,假设负重轮与地面直接接触,建立了振动系统数学模型并进行仿真分析;史力晨等[4-6]基于弹簧振子理论建立坦克悬挂系统,并考虑路面系统及上装武器系统对车体振动的影响,建立了坦克整车二维解析模型;陈兵等[7]基于多体动力学理论建立了高速履带车辆动力学模型,对悬挂系统的非线性进行了研究;韩宝坤等[8]通过分析坦克悬架系统各部件之间接触力的作用关系,借助多体动力学软件RecurDyn建立了坦克多体系统动力学模型。孙伟等[9]研究了基于ODE(多体动力学仿真库)的履带车辆系统模型,对虚拟环境中的履带车辆行驶平顺性进行了仿真研究。上述研究工作涉及解析模型到多体动力学模型方面,但大都缺少对模型可信性的试验验证。本文通过对坦克动力学系统进行拓扑结构分析,基于多体动力学软件建立坦克多体动力学系统模型,通过实车试验的方法对该模型的可信性进行验证。
1 坦克多体动力学模型的建立
1.1 模型拓扑结构分析
某型主战坦克主要由上装武器系统、动力传动系统、车体系统和行动系统组成,行动系统主要包括主动轮、托带轮、负重轮、诱导轮以及曲臂型履带张紧机构、履带板、履带销和悬挂系统弹簧元件及阻尼元件等[10]。
建模时,忽略对车辆振动影响较小的因素,对车辆系统模型作相应简化。稳定工况下,发动机谐振频率范围是120~180 Hz,该频率远高于车体振动的低阶主频,所以动力传动系统对坦克车辆振动影响可不予考虑。车体系统进一步假设如下:
(1)乘员座椅(包括乘员)同车体的连接视为刚性连接,车体(包括动力传动系统)简化为一个刚体部件。
(2)路面为硬路面,不变形的刚体,履带与地面作用不考虑土壤的剪切变形。忽略两侧路面不平度高频成分的差异,认为两侧履带系统的输入基本相同。
(3)炮塔通过炮塔座圈固定在车体上。火炮仅通过耳轴和动力油缸与炮塔相连,耳轴处为具有黏性摩擦阻尼的旋转副,动力油缸是火炮稳定器的唯一驱动机构。
(4)履带张力符合实际工况条件,张紧机构与诱导轮之间有确定的运动关系,张紧机构通过旋转副将诱导轮与车体连接。
根据简化后部件之间的约束关系,对模型进行拓扑结构分析,如图1所示。各部件及约束明细见表1和表2。
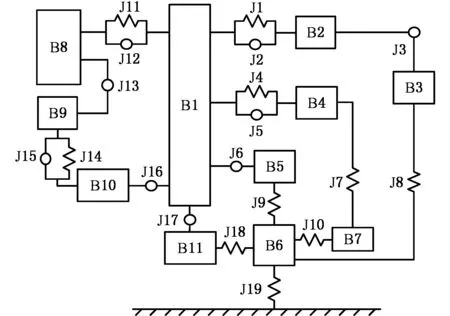
图1 模型拓扑结构图Fig.1 Topological structure of model
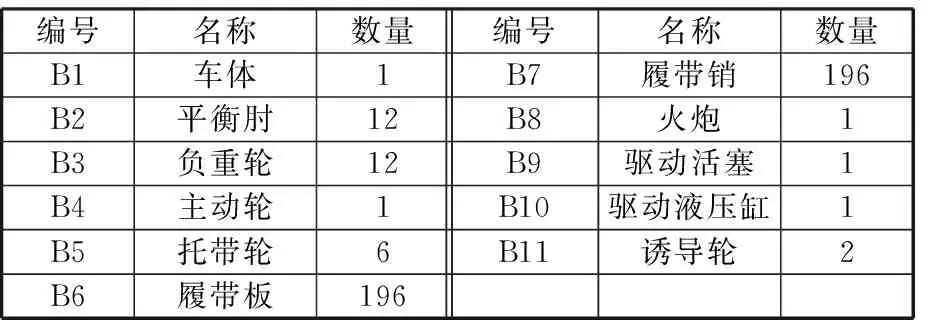
编号名称数量编号名称数量B1车体1B7履带销196B2平衡肘12B8火炮1B3负重轮12B9驱动活塞1B4主动轮1B10驱动液压缸1B5托带轮6B11诱导轮2B6履带板196
分析图1、表1和表2可知,建立动力学模型共需部件数目为426,位移约束数目为36,其中,旋转副、移动副限制的自由度均为5,模型的总自由度数为1 217。
1.2 力约束描述
图1中,约束J1为作用于车体和平衡肘之间的弹簧阻尼力矩,通过对悬架系统的扭杆弹簧-叶片式摩擦减振器等效得到[11-12],等效公式为
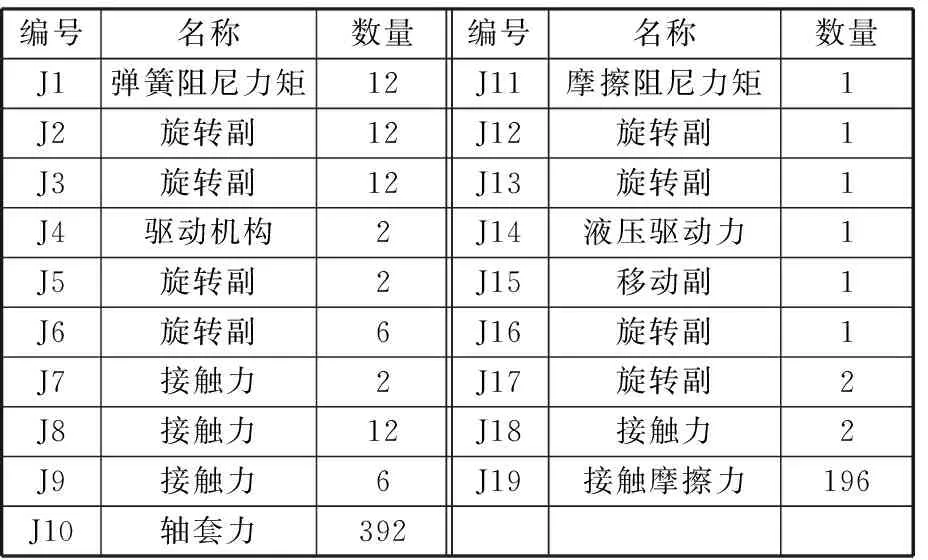
表2 约束明细表
(1)
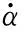
行动系统中,主动轮、诱导轮、托带轮和负重轮与履带之间通过接触力相互作用,即J7、J8、J9、J17,接触力
(2)
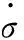
履带板与地面之间的相互作用力按接触-摩擦力约束处理,主动轮的驱动力矩J4、液压驱动力矩J14根据具体工况条件进行定义,其余力约束按线性弹簧阻尼力进行处理。
1.3 位移约束描述
动力学模型中任意部件用广义坐标表示为
qT=[xyzψθφ]
(3)
式中,x、y、z分别为笛卡儿坐标系下部件质心坐标;ψ、θ、φ分别为质心坐标欧拉角。
以旋转副为例,对其进行位移约束描述,旋转副限制了3个方向的平动和2个方向的转动,因此,其位移约束方程可表示为
(4)
式中,xij、yij、zij分别为部件i相对于部件j在3个方向的位移分量;θij、φij、ψij分别为部件i相对于部件j的欧拉角。
1.4 整车多体动力学建模
采用基于广义笛卡儿坐标的第一类拉格朗日方程建立坦克多体动力学模型,系统广义坐标矩阵
(5)
其中,n为模型中构件单元的数量,系统的约束方程表示为
Φ(q,t)=[Φ1(q,t)Φ2(q,t) …Φm(q,t)]=0
(6)
其中,m为系统位移约束和力约束方程数目。则动力学欧拉-拉格朗日组为
(7)

图2 某型坦克多体动力学模型Fig.2 Tank multi body dynamic model
1.5 随机路面模型的建立
路面不平度是影响车辆行驶平顺性和结构可靠性的重要因素。为了便于统计分析,通常将其简化为平稳各态历经的、均值为0的Gaussian随机过程[13]。根据GB/T 7031-2005的规定,路面不平度的功率谱密度与其空间频率在双对数坐标系下成线性比例关系,路面不平度空间频率f对应功率谱密度的拟合表达式为
Gq(f)=Gq(f0)(f/f0)-w
(8)
式中,Gq(f0)为路面不平度参考空间频率f0对应的标准功率谱密度,f0=0.1 m-1;w为频率指数。
目前,针对路面不平度的数值模拟主要依据上述理论,重构时间域和空间域内路面不平度模型。根据经典谱分析理论,任意平稳各态历经的随机信号可以展开成无限次谐波信号相叠加的过程。各次谐波幅值可以根据对应频段下路面不平度的功率谱得到,而相位由随机数发生器产生,笔者选用谐波叠加法进行路面模拟。
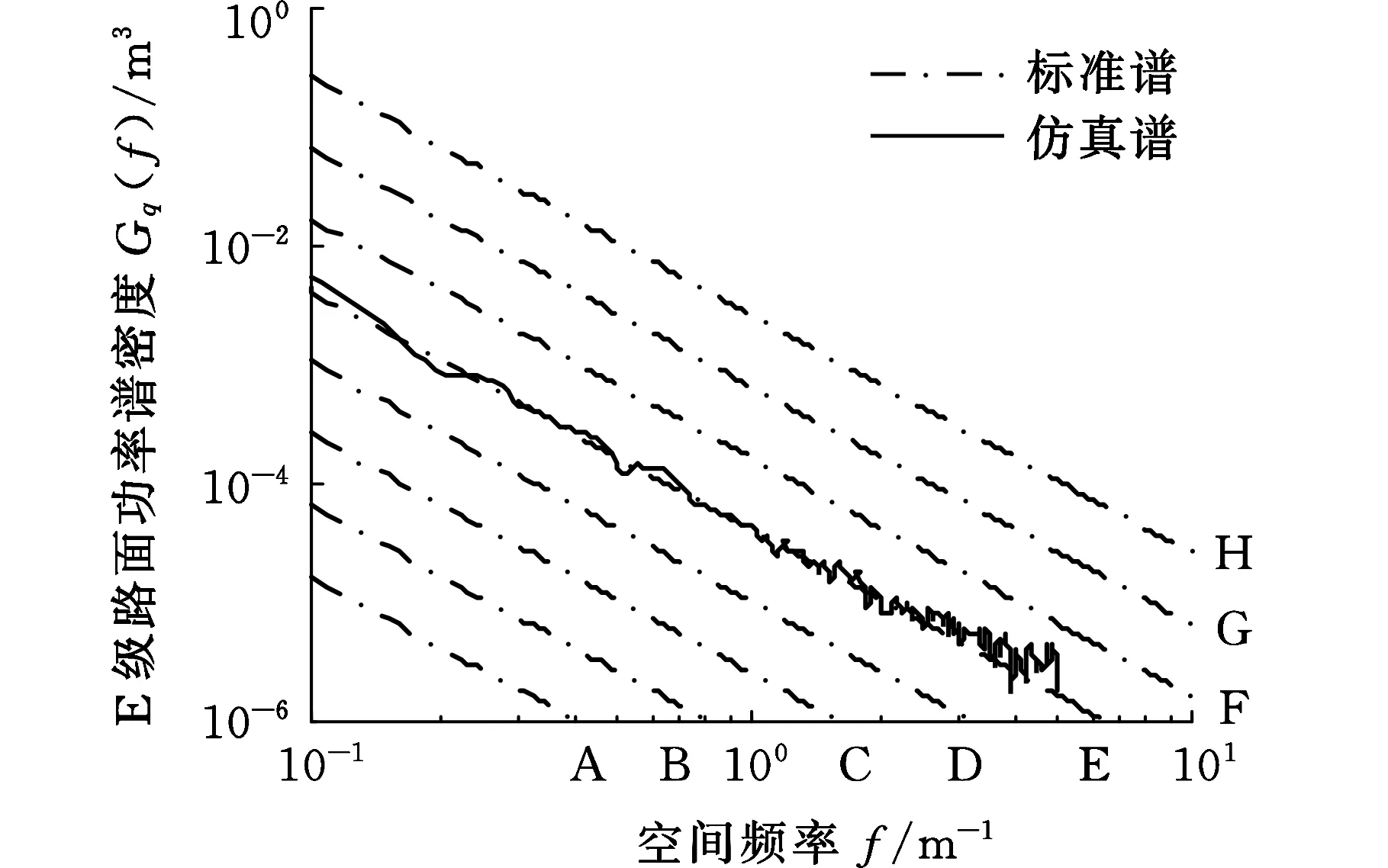
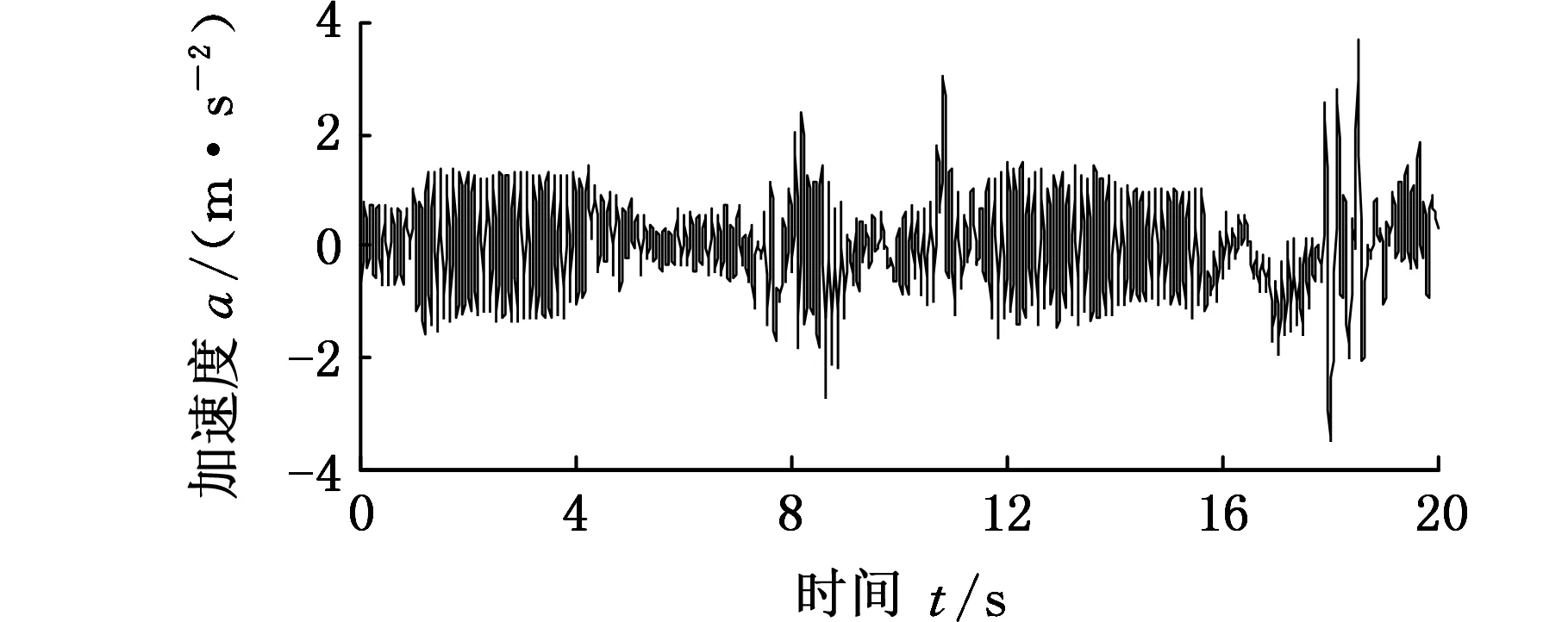
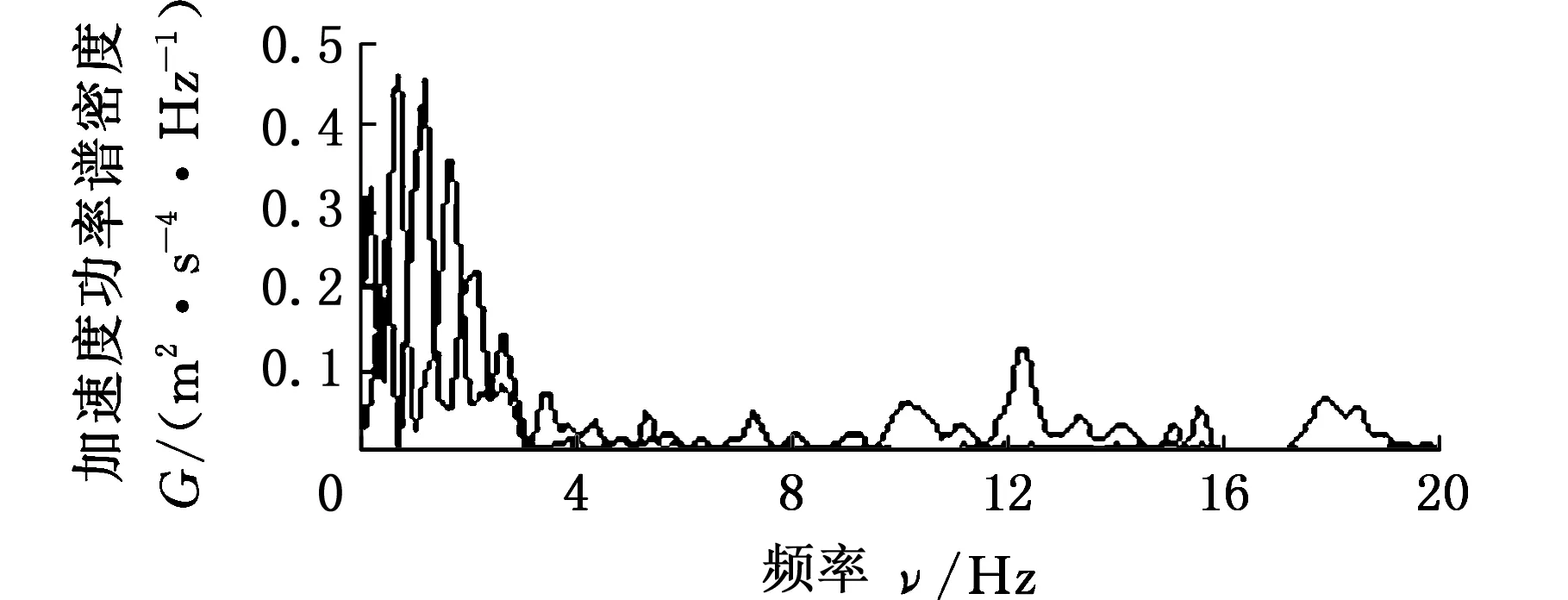
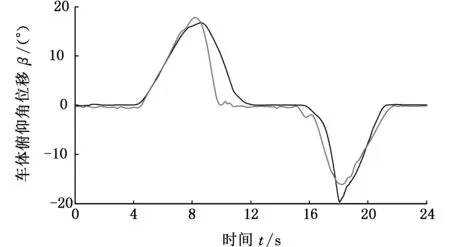
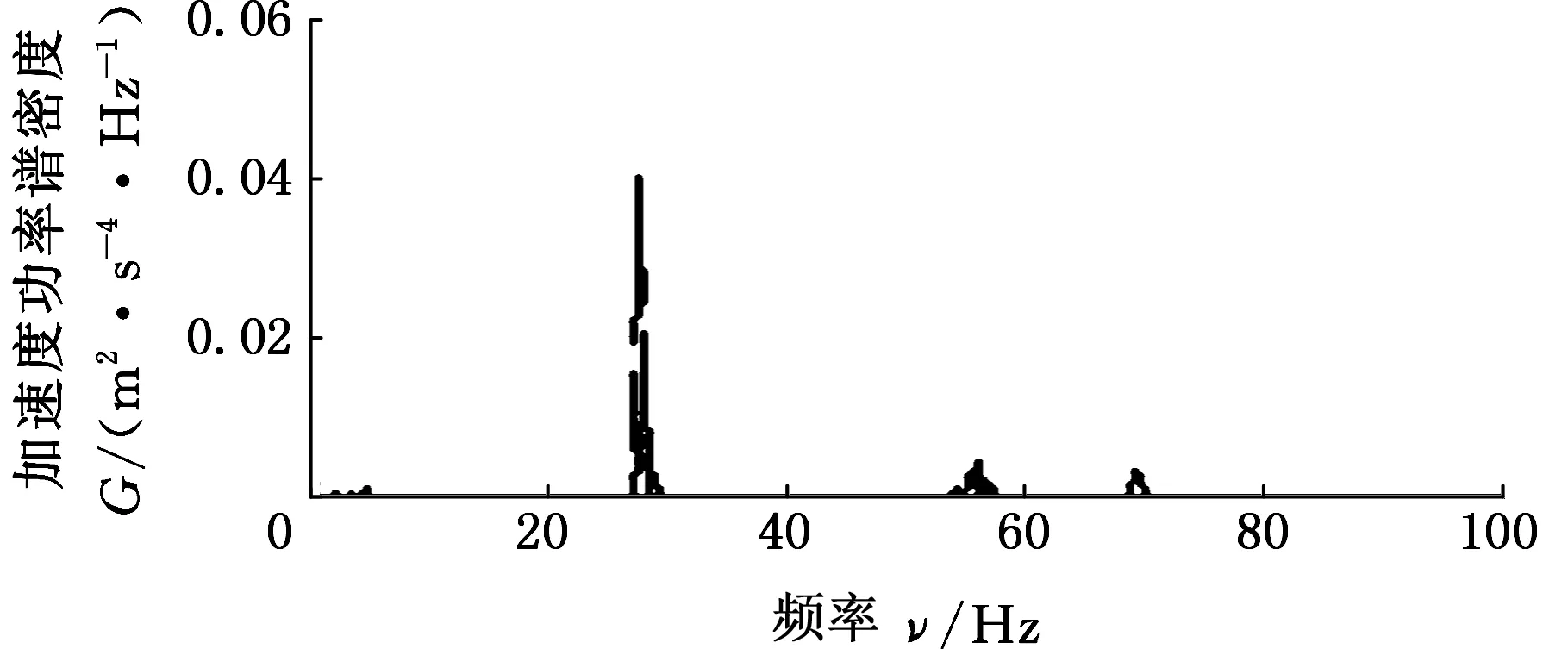
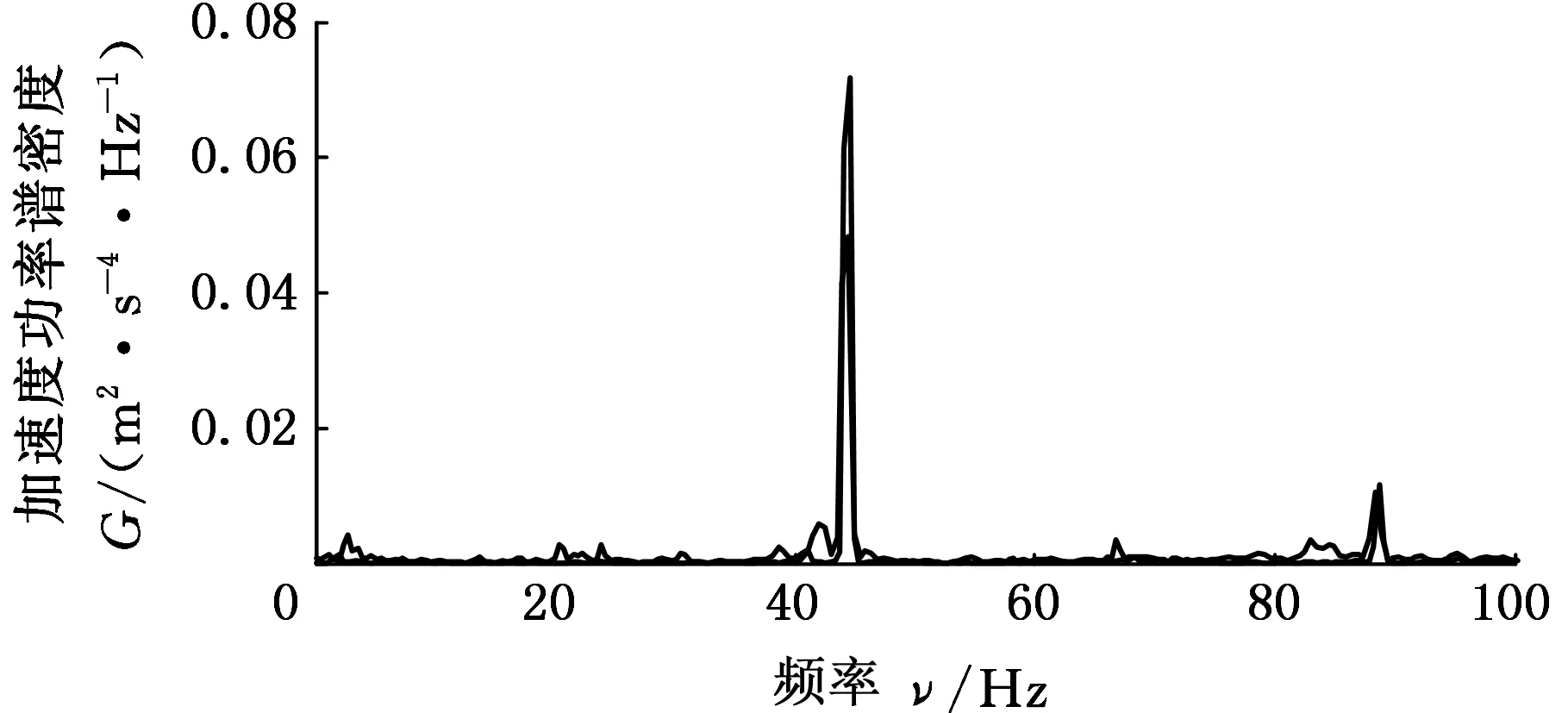
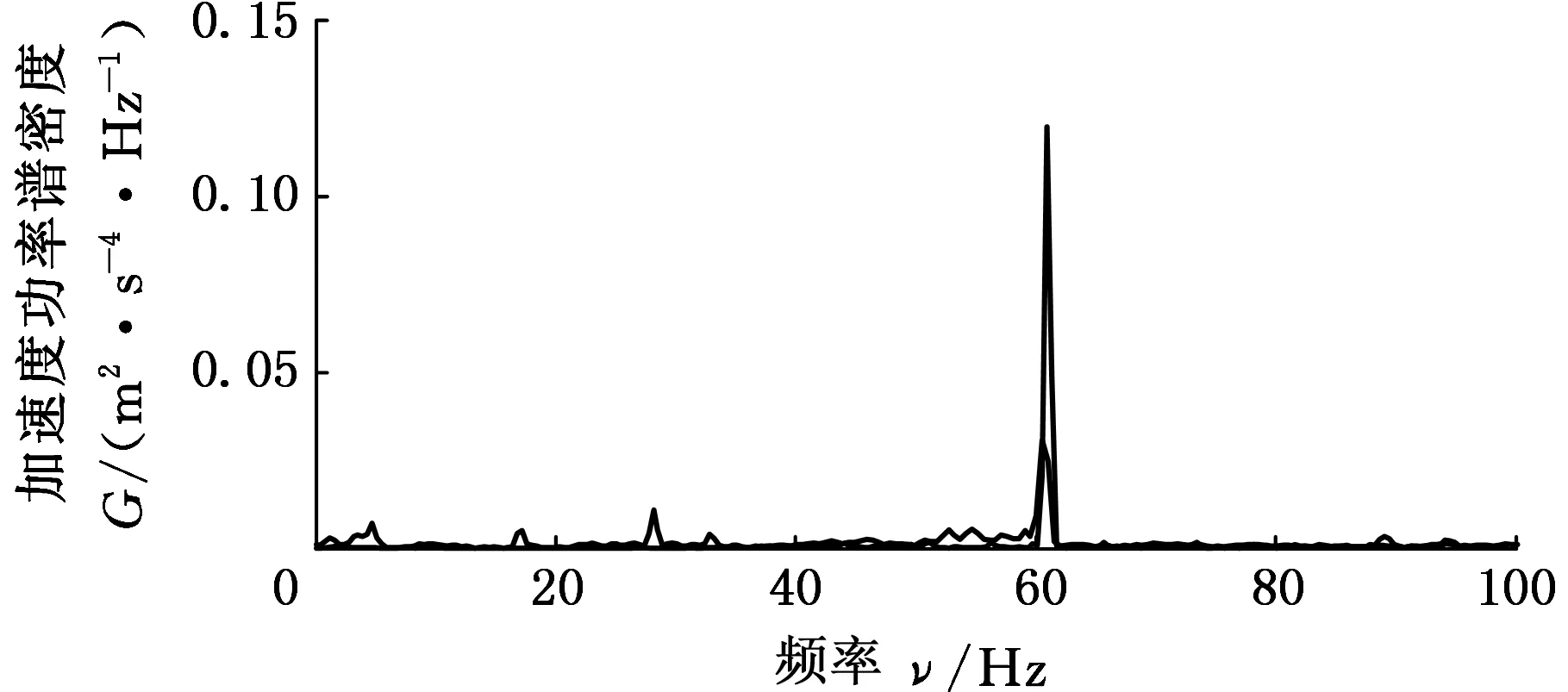
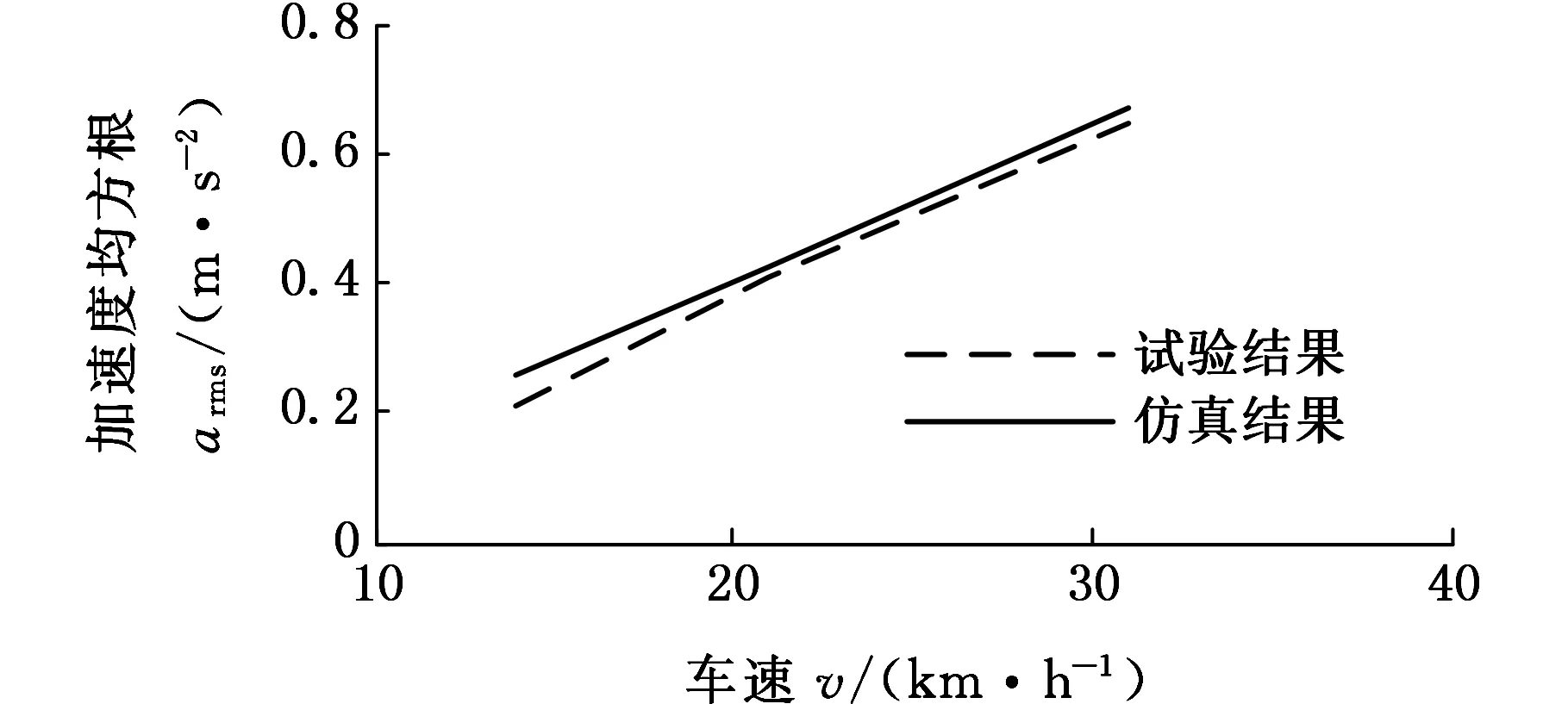
根据上述理论分析,将路面空间频率f(fL (9) (10) 式中,q(x)为路面纵向距离x对应的路面不平度;θi为[0,2π]上均匀分布的随机数;Ai为中心频率fmid-i对应的谐波的振动幅值。 在MATLAB环境下,对各种典型随机路面环境进行了模拟,以E级路面为例进行说明,E级路面和功率谱的仿真结果如图3和图4所示。 图3 E级路面模型Fig.3 Road surface model of E level 图4 E级路面功率谱Fig.4 Power spectrum of E level road (a)NI数据采集系统 (b)汽车平台 (c)车体加速度传感器 (d)负重轮轮轴加速度传感器 (e)主动轮转速光电传感器 (f)高速跑道图5 实车试验测试装置Fig.5 Real vehicle testing device 坦克实车试验测试装置如图5所示,其中NI数据采集系统实现坦克行驶过程中第一负重轮轴心上方车体和第一、六负重轮轴处的三路加速度信号数据的同步采集和主动轮转速信号的采集。 实车试验过程中,被测试车辆以1挡低速通过汽车平台,NI数据采集系统记录3个方向的加速度信号。试验过程中测得主动轮转速,再将该转速加载到仿真模型中主动轮上,驱动仿真车辆。 将实车试验测试和仿真计算得到的第一负重轮上方车体垂向振动加速度信号进行对比,采用基于周期图法改进的Welch算法对加速度信号数据和功率谱密度进行计算,通过姿态测试传感器测量得到通过汽车平台时车体的俯仰角位移变化,计算结果对比如图6、图7和表3所示。 (a)实车试验 (b)仿真结果 (c)功率谱密度对比图6 第一负重轮上方车体垂向加速度及其功率谱密度Fig.6 Vertical acceleration and PSD of vehicle body above the first road-wheel 通过图6和表3中统计数据对比可以发现,仿真结果与试验结果吻合较好,仿真数据与试验数据的垂向固有频率分别为1.51 Hz和1.54 Hz,与理论车辆垂向振动固有频率相近,通过图7中试验和仿真结果对比发现,试验和仿真结果吻合较好,车辆在5~12 s爬坡汽车平台,12~16 s在平台上稳定行驶,16~22 s车辆驶下汽车平台,试验结果验证了所建立坦克底盘模型的低阶振动特性的合理性。 图7 通过汽车平台车体俯仰角位移对比Fig.7 Comparison of pitch angle displacement passing vehicle platform 项目试验结果仿真结果误差(%)峰值(m/s2)3.70423.8925.0均方根值(m/s2)0.63950.69591.0垂向固有频率(Hz)1.511.541.3 为进一步验证仿真模型的可信性,对履带车辆直线行驶过程进行实车试验和仿真对比,实车试验选择在高速跑道上进行,并分别选取3个不同的速度挡。高速跑道如图5f所示,高速跑道路面起伏程度与B级路面相近,仿真采用B级路面与其进行对比。采集第一负重轮上方车体垂向振动加速度信号。实车试验和动力学模型仿真计算得到的加速度信号的功率谱密度对比如图8所示。 通过图8中振动加速度信号的功率谱密度计算结果对比可以发现,仿真结果和试验测试结果的主要峰值频率基本一致,2挡实车道路试验数据最大峰值频率处频率为27.8 Hz,相应的仿真数据中最大峰值频率处频率为27.6 Hz。3挡实车道路试验数据的最大峰值频率处频率为41.3 Hz,相应的仿真数据中最大峰值频率处频率为41.6 Hz。4挡实车道路试验数据的最大峰值频率处频率为61.6 Hz,相应的仿真数据中最大峰值频率处频率为61 Hz。通过理论分析[11],可以看出这是由履带板的振动引起的,因为在2、3、4挡时,车速分别为14 km/h、21 km/h和31 km/h,计算得到由履带板引起的激振频率分别为27.5 Hz、42 Hz和61.5 Hz。 通过以上仿真结果与试验结果对比看出,两者有着较好的一致性,表明所建坦克底盘动力学模型能够较为客观地反映车辆行驶的高频振动特性。 为描述仿真结果与实车试验结果的相近程度,对第一负重轮上方车体垂向振动加速度信号取均方根值,如表4和图9所示。 (a)2挡行驶工况 (b)3挡行驶工况 (c)4挡行驶工况图8 不同挡位工况第一负重轮上方车体垂向加速度响应功率谱密度曲线Fig.8 PSD of the vertical acceleration of hull above the first road-wheel 通过表4和图9中负重轮上方车体垂向振动加速度信号均方根值的统计对比结果可以看出,多体动力学模型仿真与实车试验结果基本一致,而且随着车速的提高,振动加速度信号的均方根值随之增大。通过上述实车试验与仿真结果对比,表明所建动力学模型能够较好地反映实车动力学特性。 表4 第一负重轮上方车体垂向振动加速度均方根值对比 图9 负重轮上方车体垂向振动加速度均方根值对比Fig.9 Comparison about vertical vibration acceleration of vehicle body on the top of the first road-wheel (1)坦克前两阶谐振频率在1~2 Hz之间,多为车体的一阶俯仰和二阶垂向振动,三阶振动不稳定,随车速的变化而变化,分析得出是由履带板的节距引起的。 (2)所建坦克模型与实车试验用车在第一负重轮上方车体的振动加速度功率谱密度曲线峰值点吻合较好,表明所建模型可以用于车辆行驶越野机动性分析。 (3)基于虚拟样机技术建模,为坦克行驶振动特性的研究提供了一种新的方法。 [1] 韩宝坤,李晓蕾,孙逢春.履带车辆动力学仿真技术的发展与展望[J].兵工学报,2003,24(2):246-249. HAN Baokun, LI Xiaolei, SUN Fengchun.Present State and Future Outlook of the Simulation of Tracked Vehicle [J] . Acta Armamentarii, 2003, 24(2) : 246-249. [2] FERRETTI G, GIRELLI R. Modelling and Simulation of an Agricultural Tracked Vehicle[J].Journal of Terramechanics, 1999,36(3):139-158. [3] 居乃鵕.坦克随机动态系统的计算机模拟[J].兵工学报坦克装甲车及发动机分册,1984,1(1):1-26. JU Naijun. Computer Simulation of Tank Random Dynamic System[J]. Acta Armamentarii Tank Armored Vehicles and Engines,1984,1(1):1-26. [4] 史力晨,王良曦,张兵志.基于弹簧振子理论的装甲车辆振动过程仿真[J].计算机仿真,2004,21(12):18-20. SHI Lichen, WANG Liangxi, ZHANG Bingzhi. Ride dynamic Simulation of Armored Vehicle and Experiment Validation[J].Computer Simulation,2004, 21(12):18-20. [5] 史力晨,王良曦,张兵志.坦克-火炮系统行驶间振动建模与仿真[J].兵工学报,2003,24(4):442-446. SHI Lichen, WANG Liangxi, ZHANG Bingzhi. Modeling and Simulation of a Moving Tank-gun System in Vibration [J]. Acta Armamentarii, 2003, 24(4):442:446. [6] 史力晨,王良曦,张兵志.车载火炮系统动力学仿真[J].系统仿真学报,2004,16(3):366-369. SHI Lichen, WANG Liangxi, ZHANG Bingzhi.Dynamic Simulation of Tank Gun System[J]. Journal of System Simulation,2004,16(3):366-369. [7] 陈兵,顾亮,黄华.履带车辆半主动悬挂计算机仿真研究[J].计算机工程与设计,2006,27(1):7-11. CHEN Bing, GU Liang, HUANG Hua. ComputerSimulation Study of Tracked Vehicle with Semi-active Suspension [J].Computer Engineering and Design,2006, 27(1):7-11. [8] 韩宝坤.装甲履带车辆行动装置动态性能研究[D].北京:北京理工大学,2003. HAN Baokun. Dynamic Performance Research for Travel Mechanism of Armored Tracked Vehicles[D].Beijing: Beijing Institute of Technology,2003. [9] 孙伟,张琦,孙丰,等.虚拟环境中履带式车辆运动仿真[J].计算机仿真,2008, 25(8):258-262. SUN Wei, ZHANG Qi, SUN Feng, et al. Simulation of Tracked Vehicle in Virtual Environment [J].Computer Simulation,2008,25 (8) :258-262. [10] 王钦龙,王红岩,芮强.基于多目标遗传算法的高速履带车辆动力学模型参数修正[J].兵工学报,2016,37(6):969-978. WANG Qinlong, WANG Hongyan, RUI Qiang. Research on Parameter Updating of High Mobility Tracked Vehicle Dynamic Model Based on Multi-objective Genetic Algorithm [J].Acta Armamentarii, 2016,37(6):969-978. [11] 居乃鵕.装甲车辆动力学分析与仿真[M]. 北京:国防工业出版社,2002:20-47. JU Naijun. Dynamic Analysis and Simulation for Armored Vehicle[M].Beijing:National Defense Industry Press, 2002: 20-47. [12] 丁法乾.履带式车辆悬挂系统动力学[M].北京:国防工业出版社,2004: 67-81. DING Faqian. Dynamics of Tracked Armored Vehicle Suspension System[M].Beijing: National Defend Industry Press, 2004: 67-81. [13] 王红岩,王钦龙,芮强,等.车辆行驶路面的数字化建模方法研究[J].兵工学报,2016,37(7):1153-1160. WANG Hongyan,WANG Qinlong,RUI Qiang,et al. Research on Digital Modeling Method of Riding Road of Vehicle [J] . Acta Armamentarii,2016,37(7):1153-1160.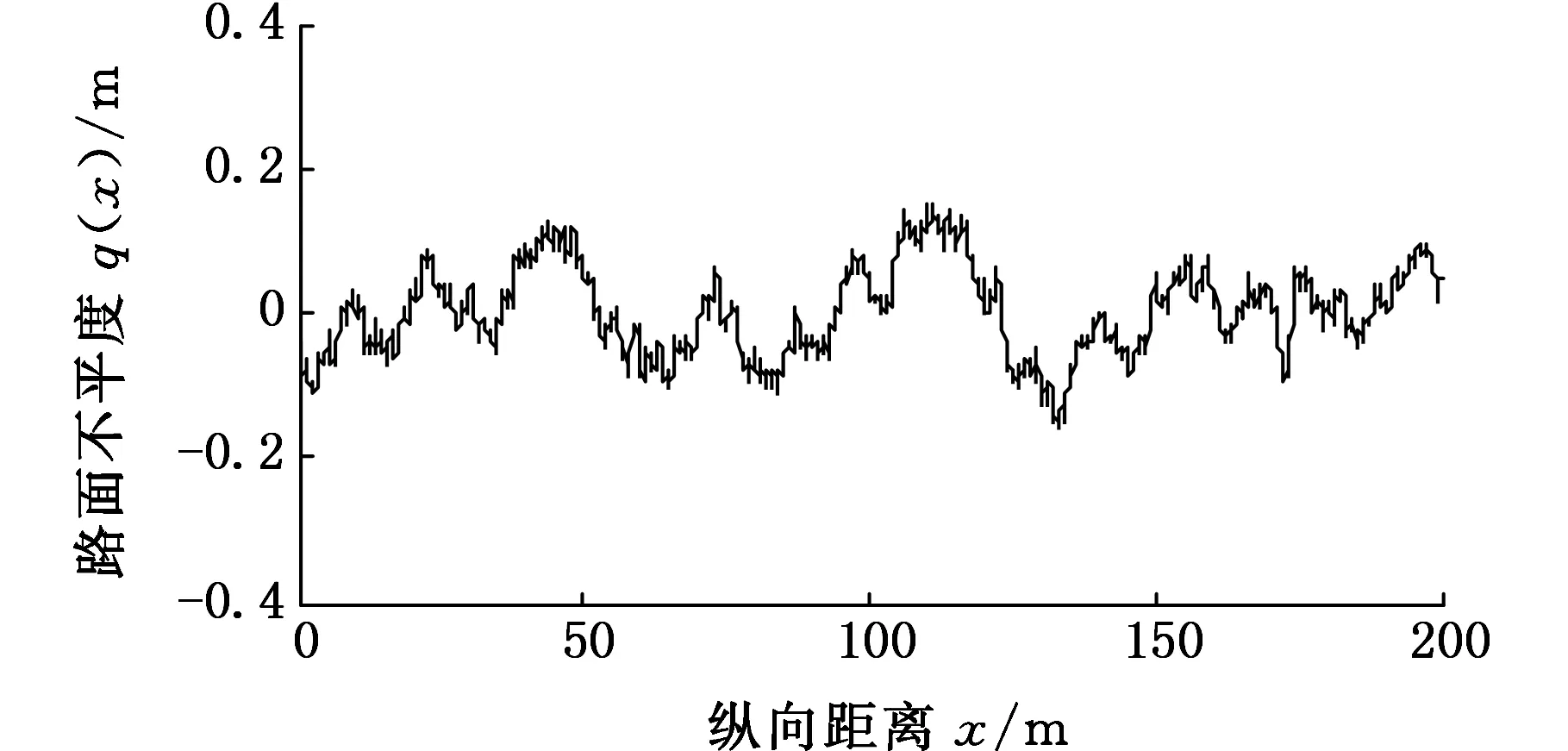
2 实车试验与模型仿真分析





3 结论

