流固耦合下轴流压气机叶片振动特性数值研究
张俊红, 付 曦, 寇海军, 林建生
(1.天津大学内燃机燃烧学国家重点实验室 天津,300072) (2.天津大学仁爱学院 天津,300000)
引 言
压气机叶片是航空发动机的关键部件之一,对压气机级负荷愈来愈高的要求导致叶片工作环境恶劣,造成各类叶片故障多发。高速旋转的叶片要承受自身离心载荷、周围气流扰动的气动载荷及力耦合作用下的振动载荷,且随着叶片向高负载、高增压比及高切线速度方向发展,导致叶片在载荷共同作用下的振动和疲劳行为更加突出和复杂。由叶片振动导致的叶片疲劳损伤是多发性的常见故障。统计表明,航空发动机中,振动故障占发动机总故障的60%以上,而叶片故障又占振动故障的70%以上[1-2]。叶片故障引起的发动机事故往往是灾难性的,会造成巨大损失,因此开展叶片的振动疲劳研究十分必要。
压气机是一复杂机械系统,诱发其叶片疲劳失效的因素较多,其中较突出的是由各类振动引起的叶片振动疲劳失效。叶片常见的振动有颤振和受迫振动。颤振是叶片的一种气弹不稳定行为,气动力场不断流入能量给叶片结构,使叶片振动不断加强,是叶片较危险的一种振动形式[3]。叶片受迫振动是另一种受外力作用不稳定振动现象,当外部激励频率与叶片自振频率一致时,即可诱发叶片共振现象,短时可使叶片振动加强且振动应力成几何级增加,造成叶片疲劳失效。这些激励源具有时间周期的多样性,且主要是由于叶片所处的复杂气动环境诱发的[4]。上述叶片的振动行为均与叶片周围气体介质的复杂耦合作用有关,国内外学者在这方面开展了诸多研究。王征等[2]基于计算流体动力学(computational fluid dynamics,简称CFD)/计算结构力学(computational structure dynamics,简称CSD)耦合算法,研究了压气机典型叶片的流固耦合(fluid-structure interaction,简称FSI)问题及颤振特性。汪松柏等[5]采用时域流固耦合方法对一级跨声速压气机叶片流场和固体域进行数值模拟,指出压气机转子叶片在气动力和离心力共同作用下的弹性变形会影响其气动特性。Lerche等[6]基于建立的压气机流固耦合时域计算模型,对叶片的动态应力分布进行了预测研究,指出流固耦合模型的引入可有效提高叶片疲劳研究的准确性。近年来,随着压气机转速和压比的不断提高,叶片所处流场环境更复杂且多频,叶片的三维特征更加明显,基于流固耦合方法可较合理地描述气体流动及叶片结构变形的物理过程[7-8],有效提高叶片振动和疲劳研究结果的可靠性。
一般认为,压气机位于燃烧室前端,可忽略温度影响,因此自身离心惯性力及其受到的气流扰动是造成叶片振动、引起疲劳失效的主要力学因素[9]。采用计算流体力学方法获取叶片表面气动参数,可准确计算叶片在复杂载荷作用下的动态应力分布[10],从而可确定疲劳失效危险点,为叶片的疲劳失效分析提供依据。笔者在建立的在役轴流压气机叶片振动及流场分析模型基础上,基于计算流体动力学和有限元方法(finite element method,简称FEM),同时考虑离心和气动载荷共同作用,结合流固耦合数值模拟,进行了多转速工况下压气机内部流场求解及叶片振动分析,得到叶片在不同转速下的动态响应特性,并根据获取的危险工况下叶片动应力分布,分析和讨论该叶片的故障机理,对故障进行初步判定。
1 叶片流固耦合振动方程
高速旋转的压气机叶片在自身质量的作用下,会产生很大的离心力载荷,且在驱动空气过程中与气流发生扰动作用,会有很大横向气动载荷作用于叶片。同时,复合载荷的作用易诱发叶片振动,使叶片产生交变的弯曲和扭转应力,造成叶片疲劳失效。笔者将旋转叶片与气流作为一个系统,把上述载荷影响因素转换成叶片结构的初应力刚度矩阵[11],进行叶片动力学方程求解。
假设转子各叶片的力学特性相同,在每个物理时间步内对叶片振动方程求解,叶片的结构振动微分方程为

(1)
其中:M,K和C分别为叶片质量矩阵、刚度矩阵和阻尼矩阵;u表示结构位移;等式右边F为外部激励载荷。
叶片和气流的相互作用会使其各自的运行状态、系统动量和能量发生改变。高速运转的叶片会产生较大预应力作用,运动状态下叶片的固有特性必然区别于其静止状态。在研究中通过在叶片的结构面上附加一个初应力刚度矩阵来实现旋转预应力和流固耦合面压力对叶片动力特性的影响,形成考虑旋转预应力和气动压力作用的叶片振动方程。
(2)
其中:Ma为气体等效质量矩阵;ρa为气体密度;A为流固耦合矩阵;Kr为离心应力刚度矩阵;Ka为气体等效刚度矩阵;v为耦合流场作用等效位移;f为结构外载荷向量。
为了研究气动载荷作用下的旋转叶片动态响应特性,将外部载荷F导致的位移转化为结构的额外刚度。不考虑阻尼作用,且未考虑自由流场中流体位移及压力变化影响,求解
Ku0=F
(3)
其中:u0为基于静态分析的结构应力位移。
通过式(3)可以获得旋转预应力效应矩阵V。考虑旋转预应力效应矩阵的影响,并忽略阻尼项,获得旋转叶片的动力学求解方程为
(4)
2 叶片结构计算模型
2.1 叶片模型
笔者以轴流压气机高压五级动叶(图1(a))作为研究对象。该叶片由叶身和叶根部分构成,叶身为变截面扭叶片,叶根为燕尾型榫,叶高为154.8 mm,初始扭转角为33.4°。研究表明,叶片造型的微小变化可导致叶片不同的气动、振动及疲劳行为[12]。为了得到与实物叶片吻合度较高的计算模型,尽量减小模型误差对研究结果造成的影响,笔者利用ATOS三维坐标光学扫描系统(图1(b))实现实体叶片的形貌坐标数据获取(图1(c)),通过对后期坐标数据的逆向处理,实现叶片计算模型的建立(图2(c))。整个叶片形貌坐标数据获取过程如图1所示。

图1 叶片形貌坐标数据获取Fig.1 Blade geometry data acquisition
在叶片的建模过程中,叶身部分由于其变截面扭转特性,建模较为复杂。笔者采用曲线、曲面相结合拟合方式构建,即先通过7段线法[13]创建一些特征边界线,后采用最小二乘法,通过特征边界线及其包络的坐标数据点拟合叶身曲面,最终拼合曲面完成整个叶身绘制,如图2所示。

图2 叶片计算模型Fig.2 Blade calculation model
2.2 叶片有限元模型
为了更好地描述叶片的薄壁特性,采用10节点四面体单元(solid 187)对叶身及其榫部进行网格划分,如图3(a)所示。考虑叶片实际工作过程中,叶片与轮盘采用燕尾榫方式进行装配,因此对叶片榫头与榫槽接触的表面施加法向约束,榫头前后施加轴向约束,如图3(b)所示。压气机叶片材料为TC4(Ti-6Al-4V)钛合金,其主要力学参数[14]如表1所示。

表1 TC4钛合金主要力学参数Tab.1 Mechanical property parameters of TC4

图3 叶片网格模型及其约束Fig.3 Blade model mesh and boundary conditions
2.3 有限元模型验证
为了保证叶片计算模型对实际模型的拟真度,通过实际叶片的振动试验对叶片计算模型进行拟真度校核[15],整个试验过程如图4所示。
试验在室温条件下进行,将叶片固定在试验台基础上(图4(c)),LMS Test.lab振动测试系统(图4(b))连接加速度传感器和压电式力传感器,通过单点激励、单点响应的方法测取叶片的固有频率和模态振型。IH-01型压力传感器实时记录力锤激励力大小,PSV-400-3D型激光测振仪作为加速度传感器(图4(e)),通过非接触式测量获取叶片在激励作用下的动态响应情况,将采集的信号传入测试系统进行数据处理与分析。叶片模态试验与有限元模拟对比结果如表2,3所示,叶片前6阶固有频率的有限元计算结果与试验值相对误差均在10%以内,且前6阶模态振型计算值和试验结果均较吻合,如表3所示。因此,可认为笔者建立的计算模型在保证精度的基础上,满足后续分析需要。造成误差的原因:逆向建立的叶片计算模型无法完全逼近真实叶片,建模过程会引入一定模型误差,且有限元模态计算的约束条件无法与试验过程中的约束条件一致,也会引入一定约束误差。

图4 叶片振动特性试验Fig.4 Laboratory modal test

表2 叶片试验模态与计算模态频率对比Tab.2 Validation results for the finite element model
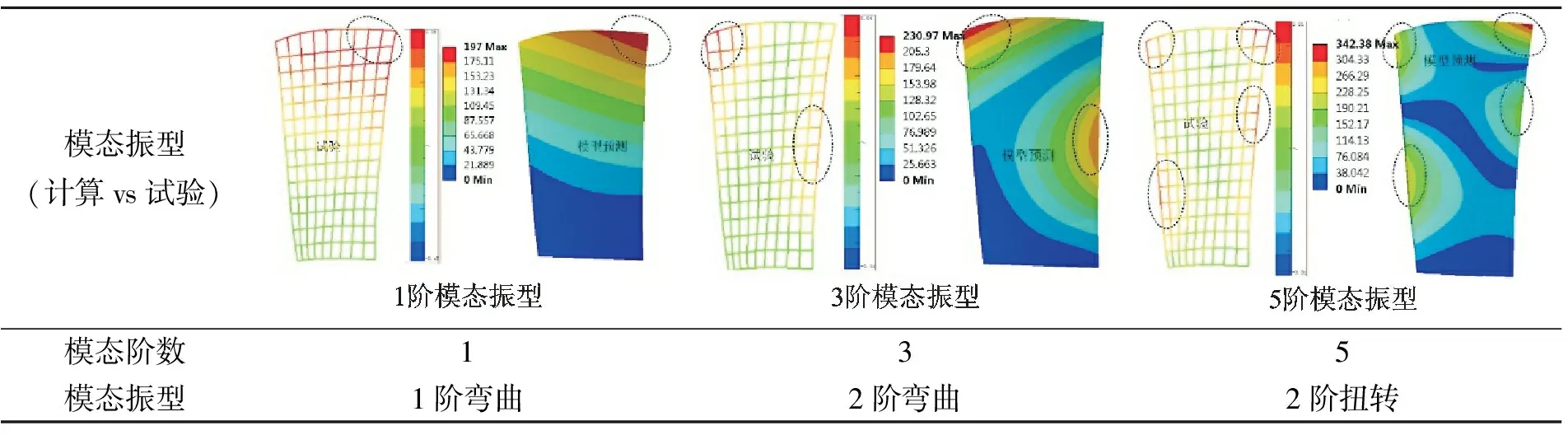
表3 计算模态与试验模态振型对比Tab.3 Modal shape comparison between laboratory tests and simulation
3 流场计算
3.1 典型工况及载荷分析
航空发动机一个完整工作循环大致分为起飞、爬升、巡航、进近和着陆5个阶段[16]。对于压气机叶片,在不同工作状态的区别主要体现在转速上。笔者基于发动机试车数据,将该发动机的完整工作循环简化为起飞、中间、最大连续、巡航和慢车5个典型工作状态,如表4所示。发动机运行过程中,叶片主要受到3类载荷作用:叶片旋转产生的离心载荷、气体流动产生的气动载荷以及气流激振力引发的振动载荷。离心载荷与气动载荷应力水平较高,容易导致叶片发生疲劳失效,而振动载荷应力水平较低,应力状态复杂,会加速裂纹扩展,缩短疲劳裂纹扩展寿命。因此,笔者在进行应力分布规律及疲劳寿命预测研究时,主要考虑离心载荷和气动载荷的影响。

表4 发动机典型工作状态Tab.4 Typical operating conditions of engine
3.2 流场分析
叶片流场物理模型如图5所示。根据该型航空发动机维修手册,设置叶尖间隙为1.7 mm。为稳定气流、改善流场计算的收敛性,添加进、出口流道,设置进口流道长度为80 mm,出口流道长度为120 mm,以减小进出口边界压力反射对流场计算域的影响。利用商用前处理软件对叶片流场模型进行网格划分,流体网格采用多块结构化网格,叶片周围采用正交性较好的O型网格,其他区域采用H型网格,叶间间隙内采用蝴蝶型网格,叶顶和机匣网格实行匹配划分[17]。利用FLUENT软件对典型工况下的压气机叶片表面气动载荷进行数值模拟。计算模型采用压力进口和压力出口边界条件,前后壁面设置为旋转周期性边界,流场下端壁面应用无滑移壁面条件。笔者认为计算流场处于湍流状态,选择k-ε湍流模型和标准壁面函数,利用隐式算法和2阶迎风格式进行求解。

图5 叶片流场计算域及流场网格Fig.5 Computational domain of flow field and meshing details
流场网格密度会影响流场计算结果,不同网格数目下叶片表面气动压力计算结果差值处于2%以内时[18],认为计算结果不受网格密度的影响。为保证流场计算结果的准确性,划分3组不同疏密的流场网格模型进行流场网格独立性验证计算,分别为粗网格(包含1,312,442网格单元)、中密网格(包含1,880,936网格单元)及细网格(包含2,516,523网格单元)。进行网格加密时应在叶片高压力梯度区域适当加密,通过监测不同网格密度下不同高度叶片的压力波动来验证流场计算结果的网格无关性,如图6(a)~(c)所示。计算结果表明,相比中密和细网格,粗网格的流场计算结果产生较大计算误差,而中密和细网格计算结果相差在2%以内,考虑计算资源和时间消耗,认为中密网格基本满足本次计算需求,因此188万网格满足本研究中的叶片表面压力计算需求。
当外激励不能激发结构共振,或其输入的能量不足以维持结构共振,叶片运行状态稳定,否则叶片的振动被加强,增加的振动应力易导致叶片疲劳。由离心拉应力叠加气动载荷引起的叶片振动交变应力,极有可能导致叶片疲劳断裂失效,因此在叶片振动分析中综合考虑了离心和气动载荷作用。作用于叶片的离心载荷通过在有限元计算中定义叶片绕旋转轴的转速获取,而气动压力载荷则通过FLUENT计算得到。

图6 叶片网格无关性验证Fig.6 Grid convergence testing
4 数值计算与分析
4.1 叶片动频分析
选取该发动机的6个额定试车工况进行叶片固有频率计算,绘制用于叶片共振分析的坎贝尔图。同时考察了流固耦合作用对叶片频率响应特性的影响,将单独离心载荷作用和流固耦合作用下的叶片频率响应进行对比,如表5所示。叶片承受载荷后,其整体刚度增大,随着转速的升高,叶片的固有频率增大。考虑气体对叶片结构作用后,叶片1,3阶固有频率减小,2,4,5,6阶增大,即引入气动力作用造成以弯曲为主振型的频率降低,扭转及以扭转为主的扭弯复合振型的频率提高。分析原因,在高速旋转压缩气体过程中,离心载荷造成的叶身拉伸增强叶片的弯曲作用,气动力作用于叶片则会削弱弯曲效应;高压压气机5级动叶是叶身扭转的变截面叶片,空气流经叶片将增强叶身扭转效果。相比于仅考虑离心载荷作用,综合考虑离心与气动载荷后,叶片弯曲频率降低,扭转频率升高。加载情况不同,叶片固有特性的差异明显,考虑气体与叶片结构的流固耦合作用能够更加接近工程实际,提高计算结果的可靠性。因此,本研究后续计算部分均考虑离心及气动载荷的共同作用情况。
表5不同工况下叶片模型的前6阶固有频率

Tab.5 The first six natural frequencies of the blade in different engine conditions Hz
4.2 叶片振动分析
由气流扰动作用造成压气机叶片振动是导致叶片疲劳失效的主因之一。已有研究成果表明,当发动机在越过临界转速工况时,叶片很可能会发生疲劳损伤。通过坎贝尔图预测叶片危险工况,通过数值计算得到危险工况下叶片动态应力分布,并进行叶片振动特性分析,通过分析结果初步开展叶片失效分析。
4.2.1 临界工况分析
根据表5数据绘制叶片坎贝尔图,得到叶片潜在的危险共振工况,如图7所示。对于压气机叶片,当激振力频率与叶片固有频率成如下关系时,发生共振或谐共振[19]。
fd=fe=kns
(5)
(6)
其中:fst为叶片静频;fd为动频;fe为激励频率;B为旋转效应系数;ns为转速;k为结构谐波系数,当k=1时发生共振,当k≠1时发生谐共振(k均取整数)。
在坎贝尔图中,不同模态的固有频率线如图7中横线所示,不同阶次的谐波激励线如图7中斜线所示。谐波激励k=1,2,3,…是由上下游气流扰(包括进口导叶和下游静叶等结构)及流场气流分布不均等引起的低倍频。激励频率线与叶片固有频率线相交的交点转速,即为叶片潜在的共振转速工况。本研究需考虑的谐波激励因子主要包括以下几类:
1)k=66 (上游进口导叶数);
2)k=38 (下游静叶数);
3)k=16 (进口导叶和转子叶片的差值);
4) 单级压气机叶片前6阶低倍频激励。

图7 压气机叶片坎贝尔图Fig.7 Campbell diagram of compressor blade
如图7所示,叶片前6阶固有频率线与谐波激励倍频线的所有“交点”转速中,并不是所有的转速都会成为叶片危险转速工况。k=66倍频线与叶片固有频率线的交点转速,由于其远离叶片的工作转速区间,在叶片振动分析中可以忽略。交点转速4 952,5 162 r/min为k=38倍频线与第5、第6阶固有频率曲线相交的转速,其与地面慢车转速6 278 r/min比较靠近,但k=38谐波激励是由下游静叶对转叶的扰动造成,激励源位于转子叶片后端且为发动机启动过程中的瞬态转速工况,因此这些转速在振动分析中也可以忽略。同样情况出现在3 858,4 970 r/min处,为k=16倍频线与第2、第3阶固有频率线的交点转速。转速7 744,7 849 r/min为k=3,k=16倍频线与第1、第4阶固有频率线相交得到,共振态下叶片前4阶模态振型为叶片危险共振模态,且其位于发动机工作转速范围内。因此,转速7 744,7 849 r/min为叶片危险转速,在这些交点转速下叶片均会发生不同程度的谐共振,应在振动分析予以考虑。
4.2.2 叶片动应力分布及失效分析
7 744,7 849 r/min处于叶片工作转速区间,叶片在此转速下工作易诱发叶片谐振。图8,9为分别计算得到的两个转速下叶片表面的振动应力分布云图。如图8所示,字母A~E分别代表转速为7 744 r/min时,叶片1阶模态振型下的应力集中区域。图9中A1~C1代表叶片在转速为7 849 r/min时,4阶模态振型应力集中区域。叶片的1阶模态为弯曲振型,4阶模态为扭弯复合振型,叶片的应力集中区域表现出一定差异性,且最大峰值应力点出现的位置也有所区别,1阶振型出现在C1处,4阶振型出现在A1处,因此临界转速工况下叶片振动应力分布与发生共振的模态振型密切相关。叶片长期使用经验表明,叶片出现疲劳损伤的方位一般位于叶片应力集中区域。因此,基于叶片的动应力分析可用来初步判定造成叶片失效的原因。

图8 动应力分布(7 744 r/min)Fig.8 Dynamic stress distribution at 7 744 r/min

图9 动应力分布(7 849 r/min)Fig.9 Dynamic stress distribution at 7 849 r/min
笔者以某在役发动机压气机五级动叶为研究对象,对该叶片历史故障特征进行分析,发现该叶片易出现损伤的部位主要位于叶片榫头和叶片前后缘靠近叶根处,如图10所示。从数值仿真计算结果可知,对比图8叶片在7 744 r/min转速下发生1阶共振时叶片动应力集中部位,与图10中故障叶片疲劳源位置接近且大致吻合。据此可初步判定,临界转速7 744 r/min为该发动机的一个危险转速,应在前期叶片调频设计中避开该级转子叶片发生1阶共振。

图10 压气机叶片常见疲劳失效部位Fig.10 Common fatigue failure locations of a compressor blade
压气机是一个比较复杂的机械系统,造成叶片失效的因素繁多,有叶片自身的制造缺陷、机械激励和气流扰动叶片诱发的共振等均可导致叶片损伤失效。笔者主要以气流扰动作用下叶片的动应力分布研究为出发点,目前仅立足于叶片故障定性分析。后续研究中应进行叶片振动疲劳试验,深入研究造成叶片失效的定量因素。
5 结 论
1) 气动载荷的引入造成以弯曲为主振型的频率降低,扭转及以扭转为主的扭弯复合振型的频率提高。加载情况不同,叶片固有特性差异明显,考虑气体与叶片结构的流固耦合作用能够有效提高计算结果的可靠性。
2) 综合分析叶片临界转速及应力分布计算结果,表明叶片临界转速工况下叶片振动应力分布与发生共振的模态振型密切相关,可作为失效分析中重要考察的振动因素。
3) 叶片在临界转速工况下发生的1阶共振振型的动应力分布与叶片常见失效部位较为一致,该临界转速下叶片发生的1阶共振是造成该叶片失效的主要原因,且1阶共振为较危险共振模态,应根据分析结果对叶片进行调频,使叶片在此转速下避免与气流的激振频率接近或相等而发生共振。
[1] 蔡肇云, 金六周. 航空发动机强度设计、试验手册—叶片强度与振动计算[M]. 北京:第三机械工业部第六研究院, 1980: 1-68.
[2] 王征, 吴虎, 史亚锋, 等. 基于 CFD/CSD 技术的压气机叶片流固耦合及颤振分析[J]. 航空动力学报, 2011, 26(5): 1077-1084.
Wang Zheng, Wu Hu, Shi Yafeng, et al. Fluid-structure interaction and flutter analysis of compressor blade based on CFD/CSD [J]. Journal of Aerospace Power, 2011, 26(5): 1077-1084. (in Chinese)
[3] Nowinski M, Panovsky J. Flutter mechanisms in low pressure turbine blades[C]∥ASME 1998 International Gas Turbine and Aeroengine Congress and Exhibition. [S.l.]: American Society of Mechanical Engineers, 1998.
[4] Srinivasan A V. Flutter and resonant vibration characteristics of engine blades[J]. Journal of Engineering for Gas Turbines and Power, 1997, 119(4): 742-775.
[5] 汪松柏, 李绍斌, 宋西镇. 基于流固耦合的跨声速压气机叶片静气动弹性分析[J]. 力学与实践, 2016, 38(1): 38-42.
Wang Songbai, Li Shaobin, Song Xizhen. Static aeroelastic analysis of a transonic compressor blade based on fluid-structure interaction method[J]. Mechanics in Engineering, 2016, 38(1): 38-42. (in Chinese)
[6] Lerche A H, Moore J J, White N M, et al. Dynamic stress prediction in centrifugal compressor blades using fluid structure interaction[C]∥Proceeding of ASME Turbo Expo. Denmark: [s. n.], 2012: 193-200.
[7] Brandsen J D. Prediction of axial compressor blade vibration by modelling fluid-structure interaction[D]. Stellenbosch: Stellenbosch University, 2013.
[8] 陶海亮, 朱历阳, 郭宝亭, 等. 压气机叶片流固耦合数值计算[J]. 航空动力学报, 2012, 27(5): 1054-1060.
Tao Hailiang, Zhu Liyang, Guo Baoting, et al. Numerical simulation of aeroelastic response in compressor based on fluid-structure coupling[J]. Journal of Aerospace Power, 2012, 27(5): 1054-1060. (in Chinese)
[9] Ni K, Wang X Q, Mignolet M. Blade stress estimation during multiple vibratory modes[C]∥54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Boston: [s.n.], 2013: 8-11.
[10] Dhopade P, Neely A J. Aeromechanical modeling of rotating fan blades to investigate high-cycle and low-cycle fatigue interaction[J]. Journal of Engineering for Gas Turbines and Power, 2015, 137(5): 052505.
[11] 谭祯, 李朝峰, 张鹏, 等. 气动力作用下旋转叶片的动力特性研究[J]. 东北大学学报: 自然科学版, 2012, 33(7): 1017-1020.
Tan Zhen, Li Chaofeng, Zhang Peng, et al. Research on dynamic characteristics of rotating blades under aerodynamic forces[J]. Journal of Northeastern University: Natural Science Edition, 2012, 33(7): 1017-1020. (in Chinese)
[12] Huang J, Wang Z, Gao J, et al. Overview on the profile measurement of turbine blade and its development[C]∥5th International Symposium on Advanced Optical Manufacturing and Testing Technologies. [S.l.]: International Society for Optics and Photonics, 2010.
[13] Mohaghegh K, Sadeghi M H, Abdullah A. Reverse engineering of turbine blades based on design intent[J]. The International Journal of Advanced Manufacturing Technology, 2007, 32(9-10): 1009-1020.
[14] 林杰威. 涡扇发动机风扇叶片疲劳寿命评估与可靠性分析[D]. 天津:天津大学, 2013.
[15] Hou J, Wicks B J. An investigation of fatigue failures of turbine blades in a gas turbine engine by mechanical analysis[J]. Engineering Failure Analysis, 2002, 9(2): 201-211.
[16] Rolls-Royce Plc (United Kingdom). The jet engine[M]. Great Britain:Renault Printing Co Ltd, 1986: 6-43.
[17] Belamri T, Galpin P, Braune A, et al. CFD analysis of a 15 stage axial compressor: part I-methods[C]∥ASME Turbo Expo 2005: Power for Land, Sea, and Air. [S.l.]: American Society of Mechanical Engineers, 2005: 1001-1008.
[18] Jiao Kui, Harold S, Li Xianguo, et al. Numerical simulation of air flow through turbocharger compressors with dual volute design[J]. Applied Energy, 2009, 86(11): 2494-2506.
[19] Liu Yixiong, Yang Ce, Ma Chaochen, et al. Forced responses on a radial turbine with nozzle guide vanes[J]. Journal of Thermal Science, 2014, 23(2): 138-144.

