基于混合子结构法的输电导线风雨激振气动特性

周 超， 李 力， 刘衍平， 申 元

(1.华北电力大学能源动力与机械工程学院 北京，102206)(2.云南电网有限责任公司电力科学研究院 昆明，650217)

引 言

输电线路振动是一个固、液、气三相耦合的复杂现象，与线路带电与否有密切的关系。自Hardy等[1]于20世纪70年代正式报道这一现象以来，输电线路风雨激振成为严重威胁输电线路正常运行的振动形式之一。为揭示风雨激振振动机理，研究者主要采用现场观测、风洞实验、理论分析和数值模拟等方法。Battista等[2]研究输电塔在风雨载荷共同作用下的动力响应，提出了改进雨载荷计算方法，建立了更加合理的计算雨载荷压强公式。文献[3-4]通过修正模型实验法，初步解决气动弹性风洞实验中的模型设计难以同时满足相似定律和风洞尺寸要求的问题。文献[5-6]根据输电塔线体系在风雨激励下破坏的实际情况，建立了“三塔两跨”有限元分析模型，提出雨载荷的计算方法以及风湍流共同作用于输电塔线体系的荷载组合原则，分析了输电塔线体系结构动力特性及其相互关系。文献[7-9]认为输电导线表面上雨线的形成是风雨激振发生的根本原因，并分析了电晕振动和拉索式振动的耦合机理，表明输电导线带电对振动有显著的影响。然而，对于风雨激振机理尚无定论，但也达成了一些共识，认为一定风速和雨量的条件下，引起的输电线路气动力失稳是引起风雨激振的关键因素。由于实验条件的限制，发生风雨激振时输电导线受到的气动力难以测试，即非定常气动力，而气动力的分析是揭示输电导线风雨激振机理的重要手段。

为此，在借鉴拉索风雨激振机理研究的基础上[10-11]，将物理实验和CFD数值模拟结合的混合子结构方法应用到输电导线风雨激振气动力特性的研究。首先，利用自制输电导线风雨激振模拟实验装置得到输电导线和雨线子结构的动边界运动时程；随后，采用混合子结构方法计算得到了振动时输电导线模型的非定常气动力；最后，把气动力施加到输电导线模型上，将输电导线的振动响应与实验结果进行比较分析。图1为输电导线风雨激振非定常气动力系数研究流程。

1 输电导线模型风洞实验

1.1 实验工况

输电导线节段模型风雨激振风洞实验是在自制输电导线风雨激振模拟实验装置中完成，如图2所示。该风雨激振实验装置的风洞高为2 m,总长为4.6 m,宽为1.5m。风机采用北京顺通风机制造公司生产的SWF-7B混流式风机，可实现风速范围从1～28m/s连续可调。风机变频器采用东芝公司调频范围为0～50Hz的VF-S15 多功能调频装置。风雨模拟实验装置位于风洞的中间位置，由支架和人工降雨2部分组成。人工降雨装置能实现降雨强度从10～70mm/h连续可调。为保证雨滴尺寸达到要求，降雨装置正下方安装有对应孔径的雨水导流板。

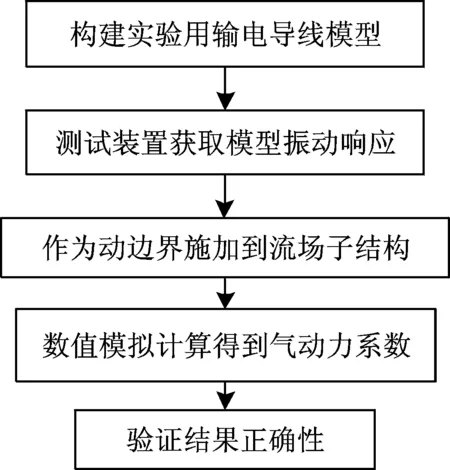
图1 风雨激振气动力特性研究流程Fig.1 Flow diagram of investigation on aerodynamic characteristics of rain-wind induced vibration

图2 风雨激振实验装置Fig.2 Test apparatus of rain-wind induced vibration

图3为输电导线风雨激振横截面模型，实际输电导线在外界环境下的雷诺数Re约为1.2×104～2.8×104，根据雷诺数计算公式Re=UD/v，(其中：U为导线截面风速；D为输电导线模型直径；v=0.150cm2/s,为流体运动的黏度)，通过计算得到输电导线节段模型直径为100 mm,雨线尺寸约放大1.5倍，雨线模型如图4所示。导线模型全长为2 m，总质量为2 kg。图5为导线在风场中布置示意。风水平吹向导线节段模型，α为节段模型的倾斜角，β为节段模型的风偏角。输电导线节段模型倾斜角和风向角如图6所示。

两端支架由电动升降装置组成，可以实现输电导线模型在风场中高度和角度的自由调节。导线模型与支架采用弹簧连接，弹簧两端分别安置两个位移传感器用来测量模型面内振动响应，导线模型两端分别安置两个加速度传感器，采样频率为50Hz，用来测量导线模型的横风向响应，振动响应的测量以及数据处理系统为德国m+p公司VibPilot 16通道信号采集系统及数据处理软件(Analyzer Revision 4.4)。

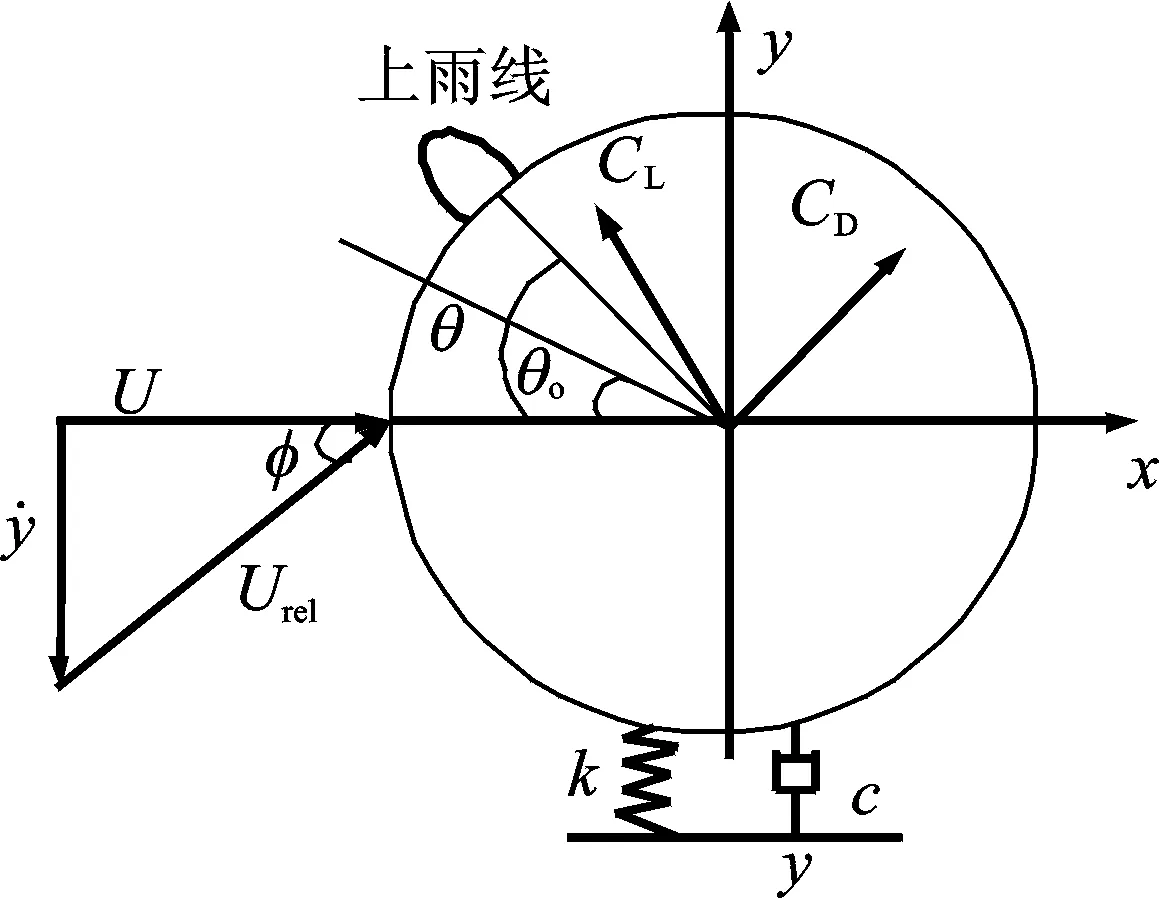
图3 导线风雨激振横截面模型Fig.3 Model of rain-wind induced vibration on the conductor

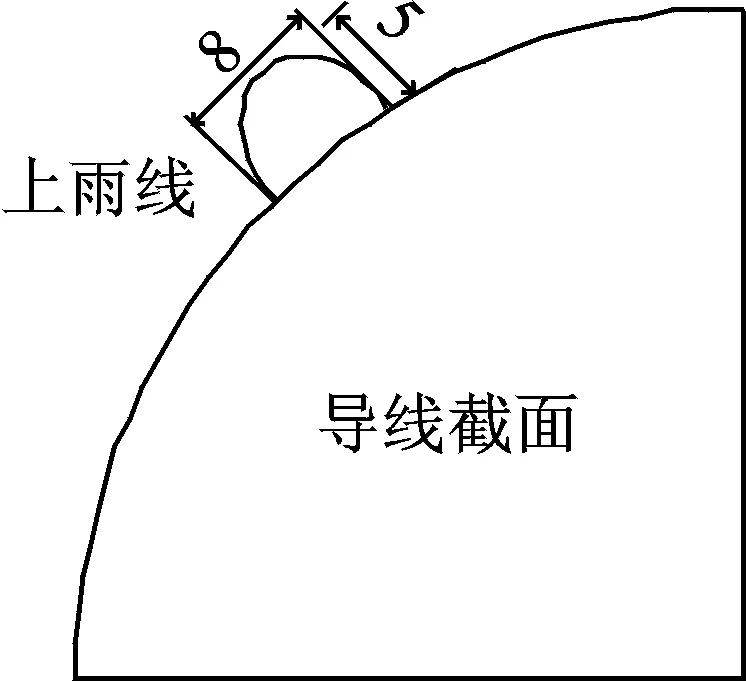
图4 雨线模型尺寸(单位:mm)Fig.4 Geometric dimensions of the upper rivulet(unit:mm)

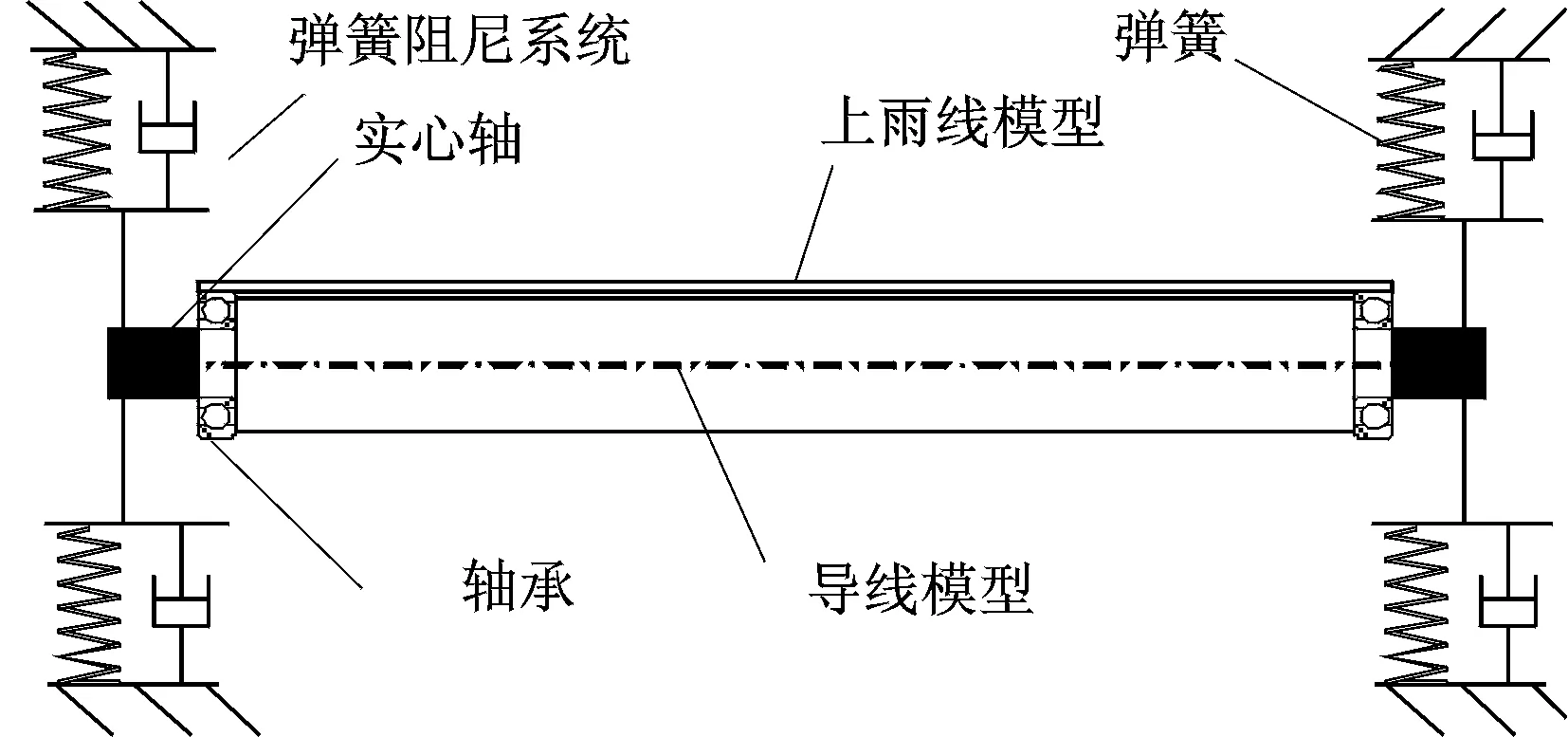
图5 风洞实验导线模型布置示意图Fig.5 Schematic diagram of testing set-up with the conductor model

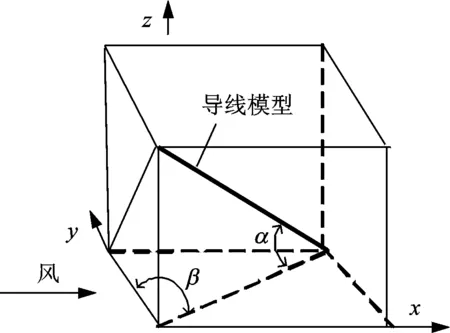
图6 导线模型倾角和风向角定义Fig.6 Definition of the inclination and wind angle

1.2 实验结果

已有研究[12]表明，风偏角β为20°～30°、风速为7～20m/s、导线倾角α为30°、上雨线位置为50°～80°时最易发生风雨激振。雨线是在风雨条件下导线表面流动的雨水，在风压力、导线表面粘滞力和重力的共同作用下，在导线表面形成沿导线轴向的连续的水线。 图7为通过此风雨激振实验装置得到上雨线在输电导线表面与水平面夹角为60°，35°和80°时，输电导线的振幅与风速的变化关系。从图中可以得出，风速达到12m/s和雨线位置为60°时，输电导线振幅明显增大。因此，本次实验主要是测试β=25°，U=12m/s，θ=60°时输电导线模型发生风雨激振时的振动响应。图8为本次实验得到的输电导线横风向振动响应。如图9所示，对其进行傅里叶变换得到振动的主频率为2.42Hz，即输电导线模型横风向自振频率，从而说明了输电导线风雨激振具有频率低、幅值大的特点。

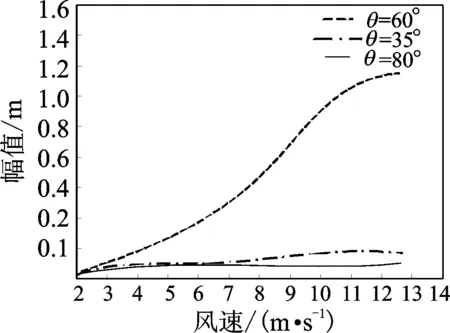
图7 振幅与风速的变化关系Fig.7 The relationship between the amplitude and wind speed

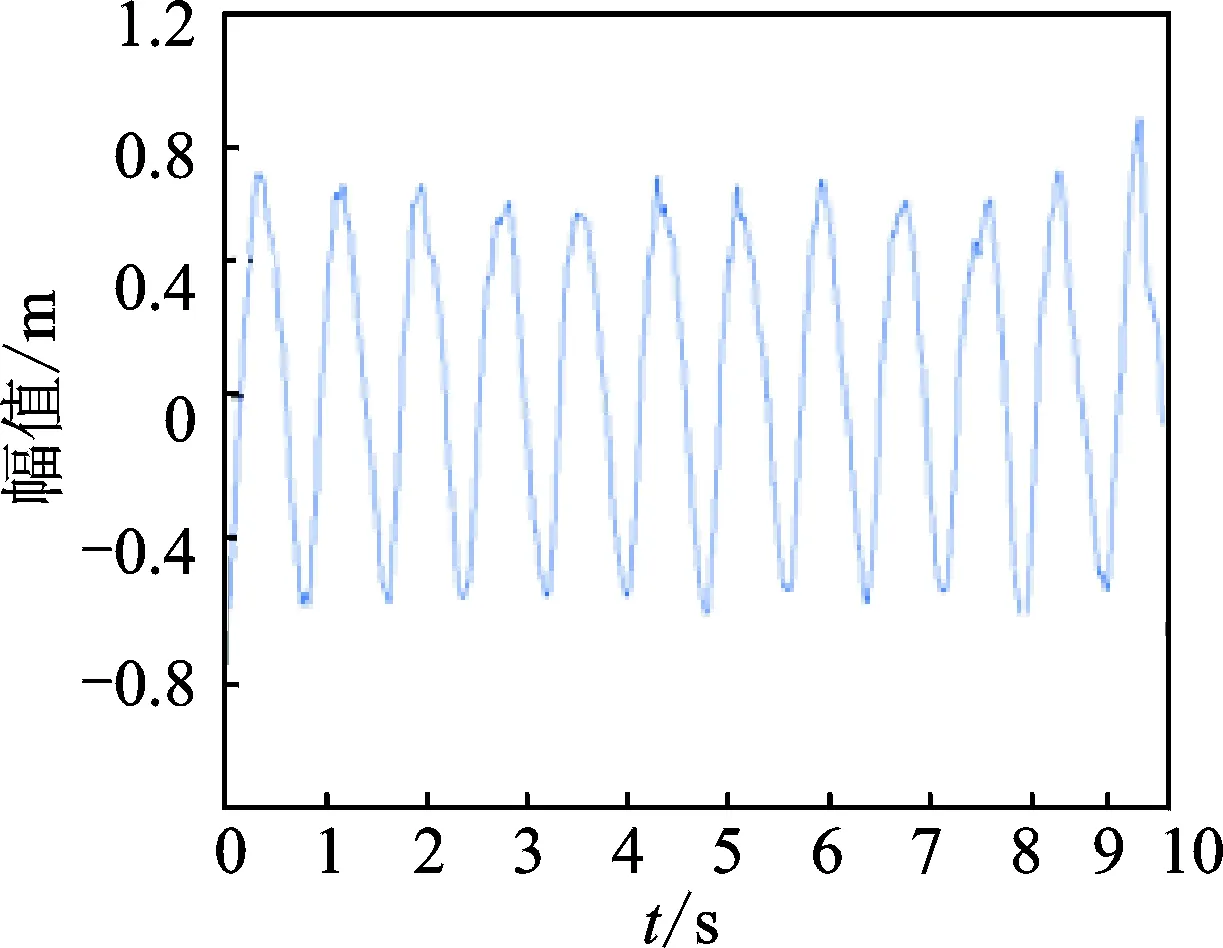
图8 输电导线振动响应Fig.8 Vibration response of the transmission line

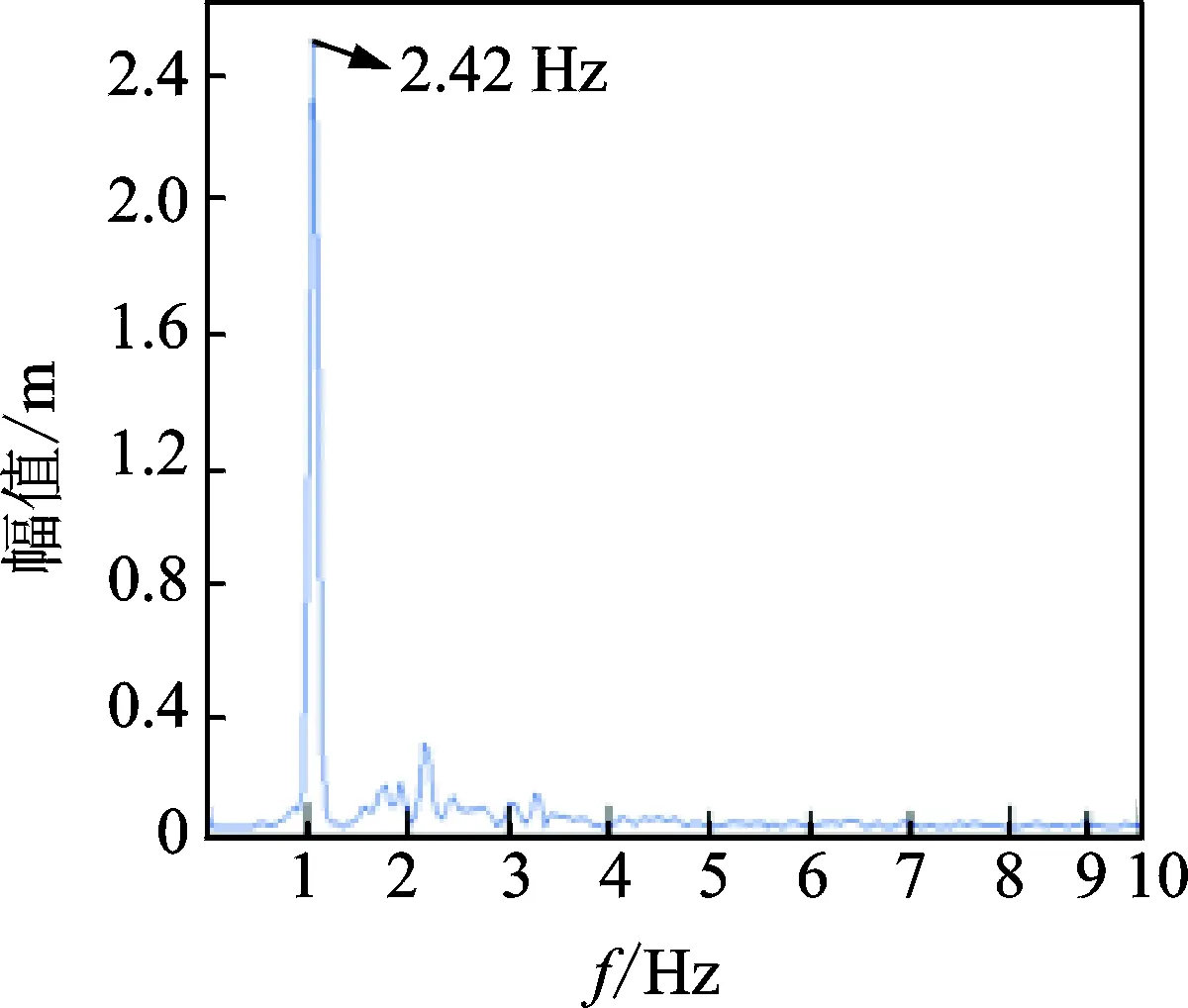
图9 振动响应频谱分析Fig. 9 Spectrum analysis of vibration response

2 输电导线风雨激振混合子结构方法

借鉴文献[13-15]提出的物理实验和数值模拟混合子结构方法对输电导线发生风雨激振时气动力特性进行研究。笔者采用的混合子结构方法示意图如图10所示，圆柱振动为弹性支撑，将圆柱振动简化为质量-弹簧-阻尼系统。导线和雨线为一子结构，其附近的绕流场为一子结构。利用已建立的风洞实验和测试系统测得输电导线的振动响应施加到结构子结构边界上，让边界按照指定的响应进行运动，计算绕流场特性，从而获得输电导线振动的气动力特性。

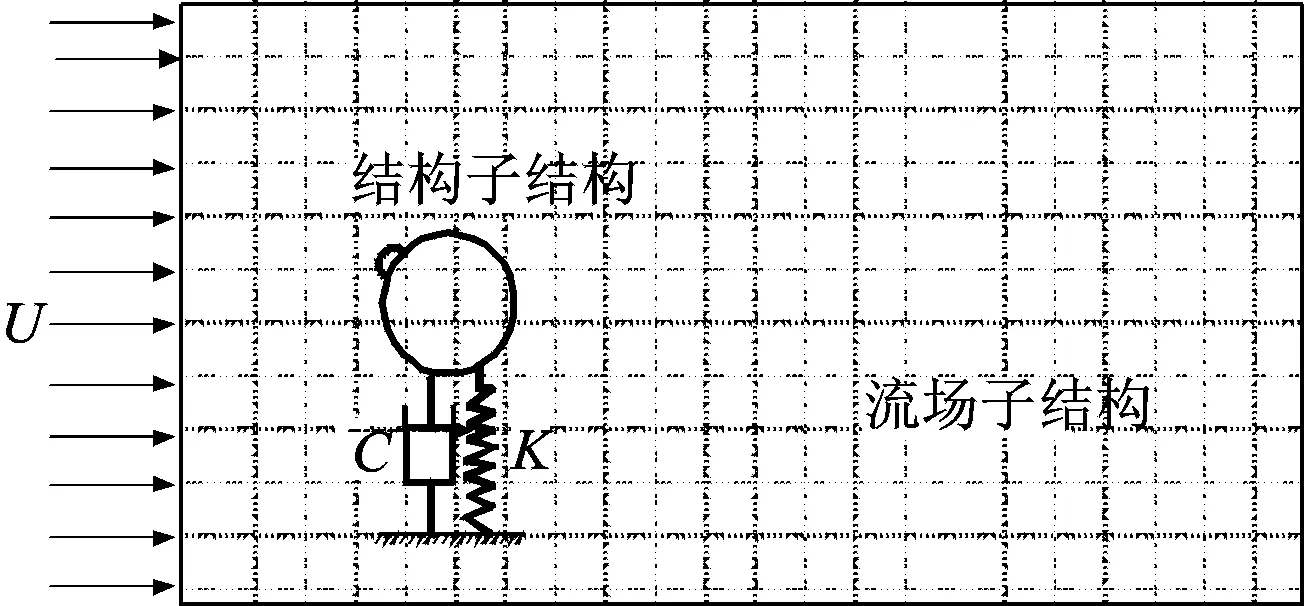
图10 混合子结构方法示意图Fig.10 Schematic diagram of hybrid substructure approach

2.1 CFD数值模拟流体模型

本次流场域计算由ANSYS Fluent 12.0 完成，图11和图12分别为二维CFD输电导线风雨激振子结构方法的流体模型和结构子结构区域的局部放大。流体域尺寸为50D×20D，结构子结构中心距上游边界10D，距下游边界40D，距离上下边界各为10D，D为与来流方向垂直的特征长度(输电导线的直径)。

笔者采用输电导线原型为LGJ-500/35，其具体参数如表1所示。边界条件设置如表2所示。

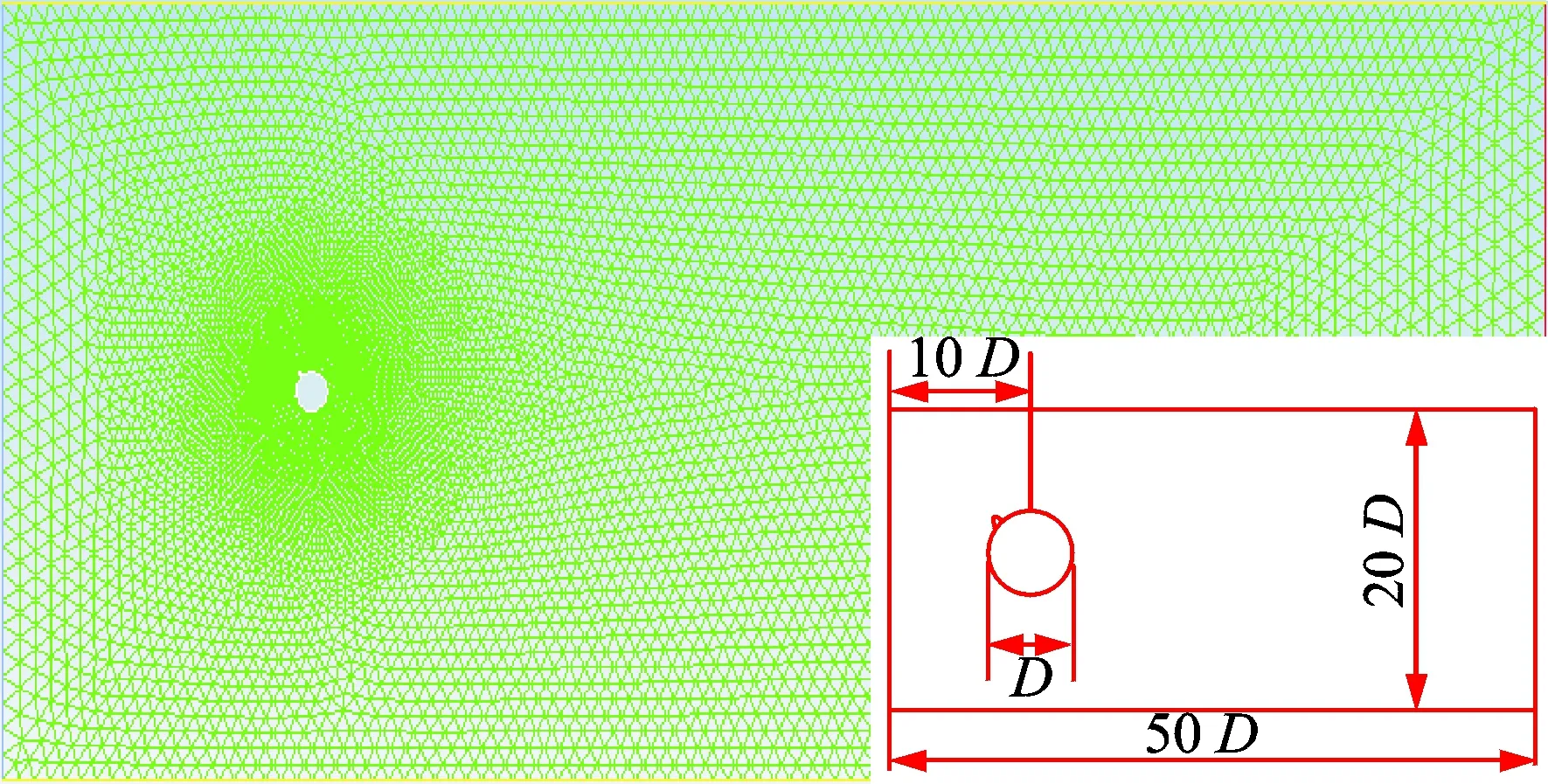
图11 流场计算域Fig.11 Computational domain of fluid field

表1 导线相关参数表Tab.1 Parameters of the conductor

表2 流场各边界参数Tab.2 Parameters of the flow field model

2.2 输电导线和雨线子结构动边界设置

本研究的湍流模型采用Fluent中基于雷诺平均N-S方程组(RANS)的模型。即采用涡粘性封闭模式中高Reynolds数，标准k-ε两方程模式。此方法计算量小，又可以较好地模拟近壁面小尺度脉动运动。运用Fluent中用户自定义函数(user defined function，简称UDF)运动宏和动网格可实现结构子结构按照指定的运动规律振动。UDF函数主要通过式(1)控制振动

cg_vel[1]=A*sin(B*time)

(1)

其中：cg_vel[1]为y方向的速度；A为振动的幅值；B为振动的频率。

动态网格再生方法主要采用弹性光顺法(spring smoothing)和局部重构(local remeshing)。弹簧光顺法中，网格线类似于弹簧，两端节点作弹性移动，在网格边界节点发生位移后，会产生与位移成比例的力，从而由力转化出节点移动的距离。通过控制弹簧光顺法中两个参数(弹簧常数和边界节点松弛因子)，将网格变化区域控制在刚体运动边界外围，因此计算时无需插值，提高计算精度。

将通过风雨激振模拟实验装置得到的输电导线振动响应图8作为结构子结构的动边界。图13为结构子结构按照动边界(UDF函数表示)运动处于某个振动周期的正方向最大位移位置、平衡位置以及负方向最大位移位置。可以看出，导线和雨线子结构振动时，流体网格变形较大。通过Fluent中局部重构方法对扭曲率较大的网格进行重构，从而保证整体网格质量，满足实验湍流模型的要求。此次仿真模拟计算每步时长为0.001s，计算步数为10 000。

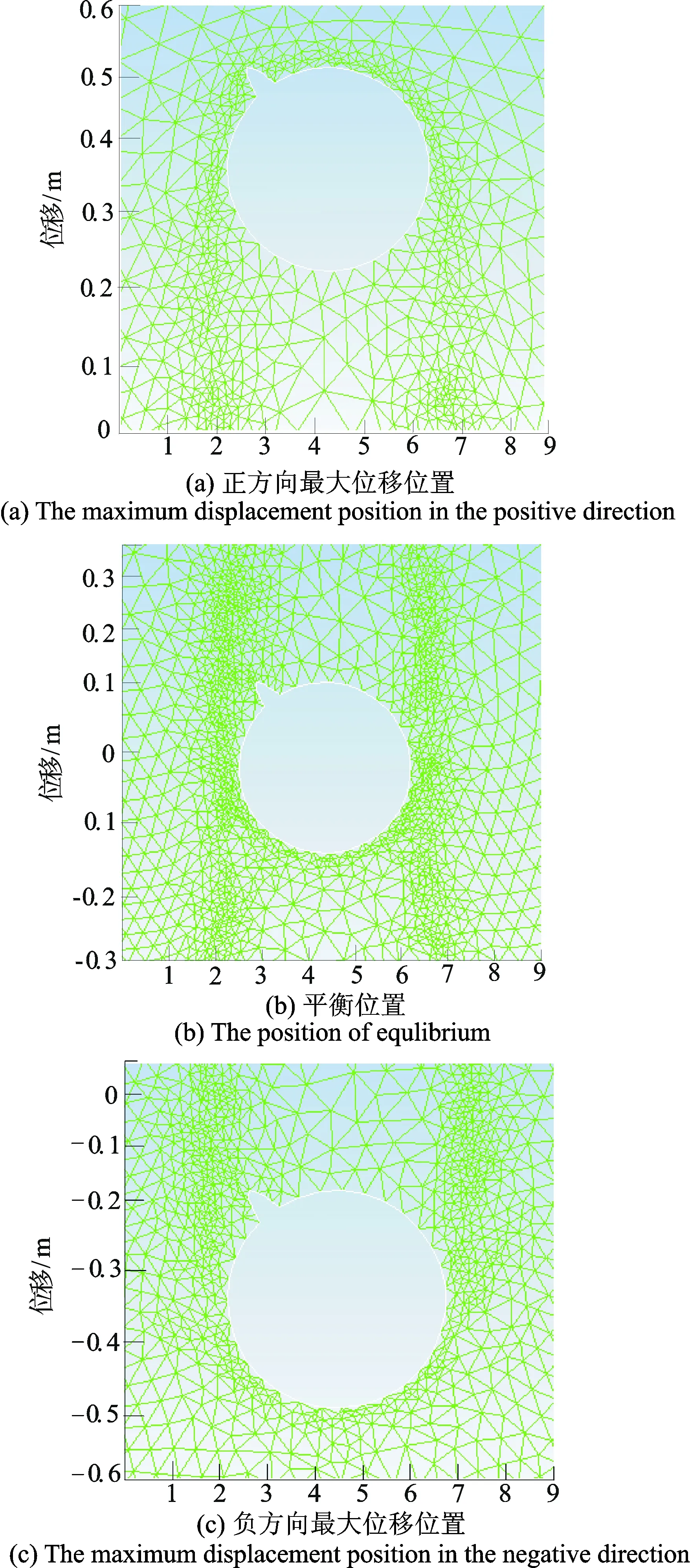
图13 结构子结构振动周期位置图Fig.13 Diagram of substructure vibration period position

2.3 混合子结构方法计算结果分析

通过混合子结构方法得到输电导线风雨激振非定常气动力系数(升力系数和阻力系数)如图14和图15所示。计算得到升力系数均值CL=-0.35，阻力系数均值CD=1.2。图16和图17为对平稳段升阻力系数进行快速傅里叶变换，得到主频率为2.42Hz。气动力系数的主导频率等于输电导线自振频率，从而验证了文献[7]提出的气动力对输电导线做正功且与频率相同是导致输电导线风雨激振发生的结论。

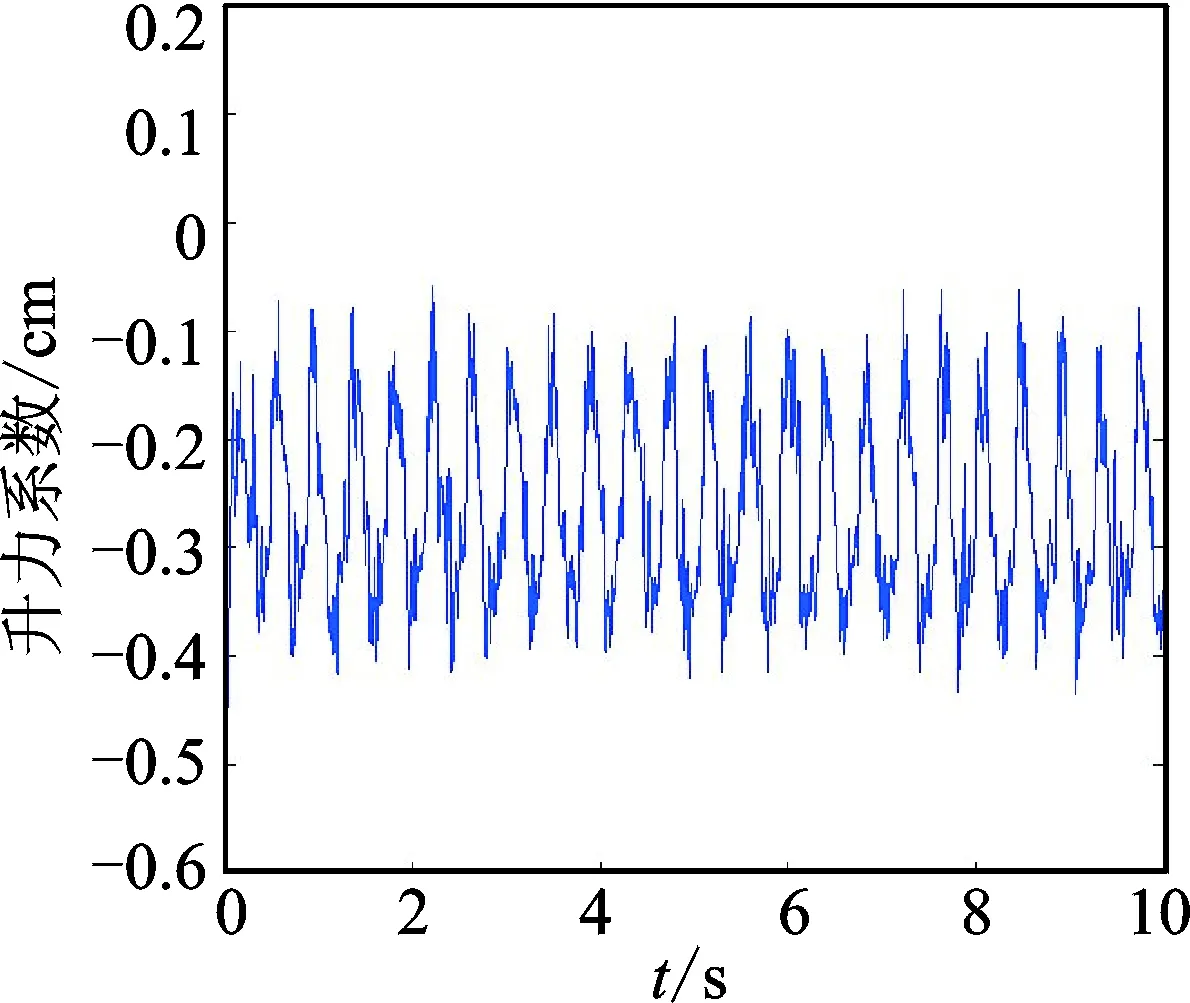
图14 升力系数Fig.14 Aerodynamic lift coefficient

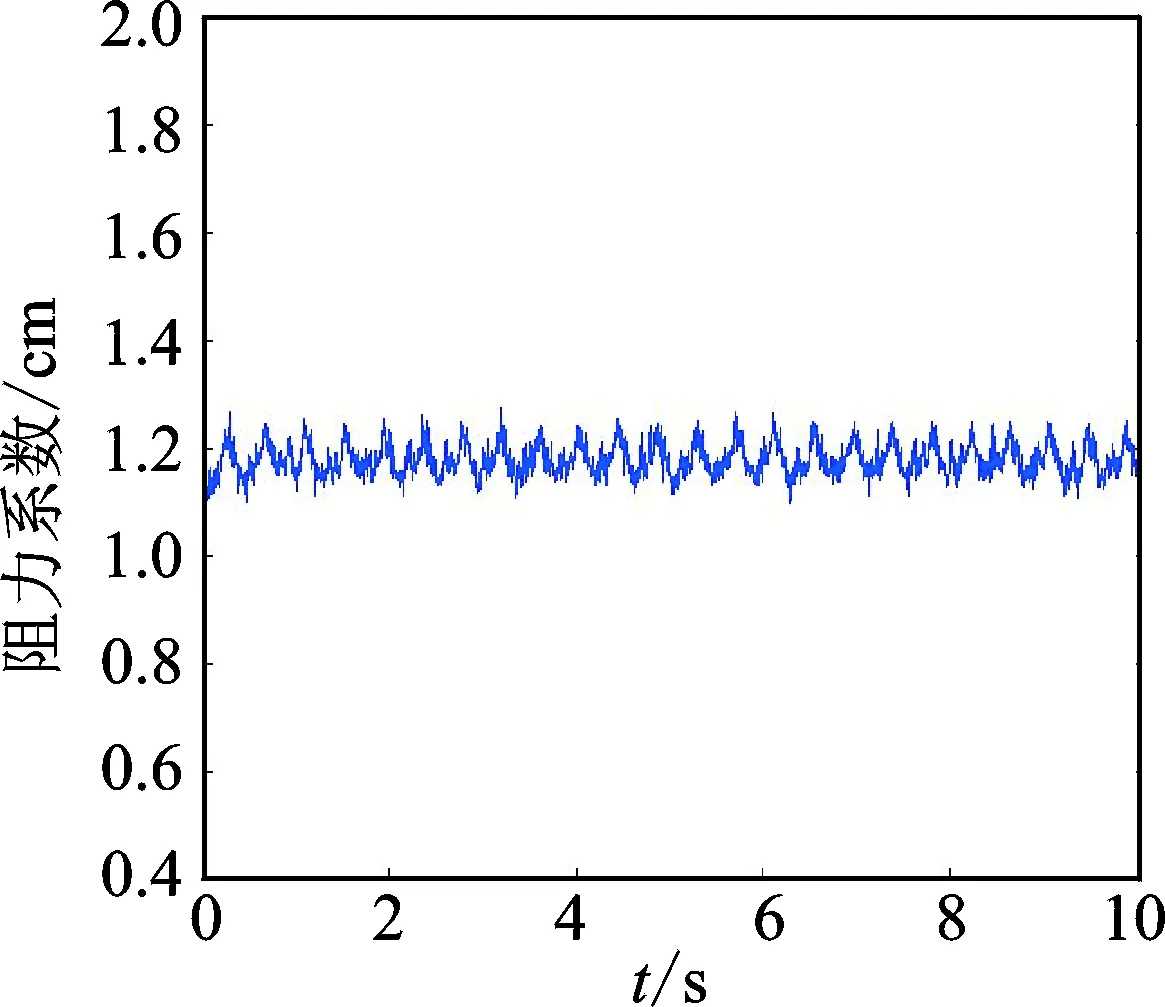
图15 阻力系数Fig.15 Aerodynamic drag coefficient

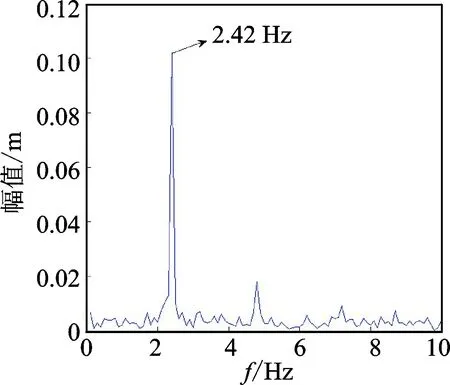
图16 升力系数频谱分析Fig.16 Spectrum analysis of aerodynamic lift coefficient

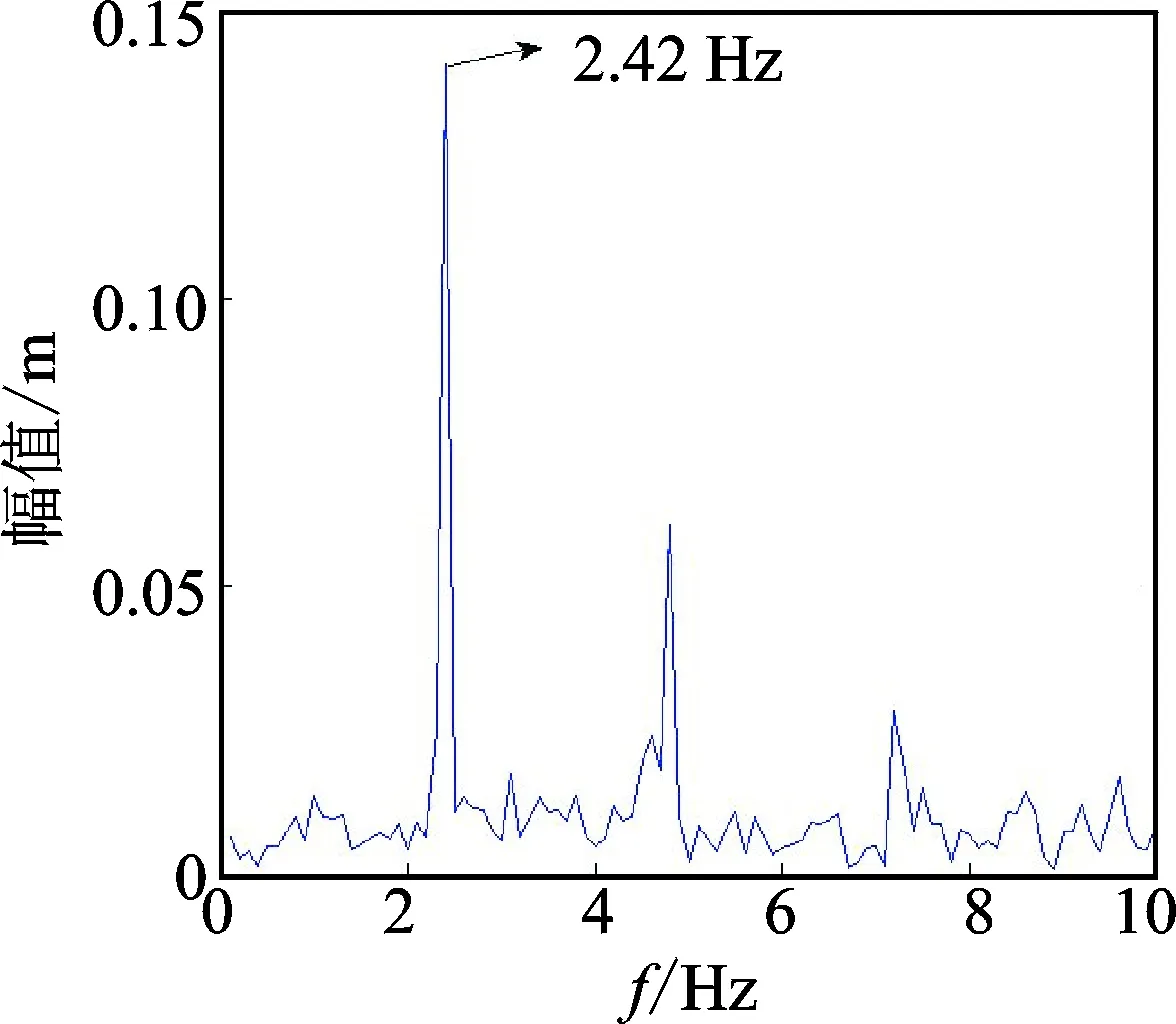
图17 阻力系数频谱分析Fig.17 Spectrum analysis of aerodynamic drag coefficient

3 混合子结构方法结果验证

输电导线节段模型横风向振动运动方程为

(2)

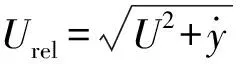
采用Newmark-β法对式(2)进行求解，得到输电导线的振动位移时程如图18所示。通过与风洞实验结果进行对比发现，数值求解结果与风洞实验结果吻合较好，说明混合子结构方法能够求解出输电导线风雨激振非定常气动力系数。

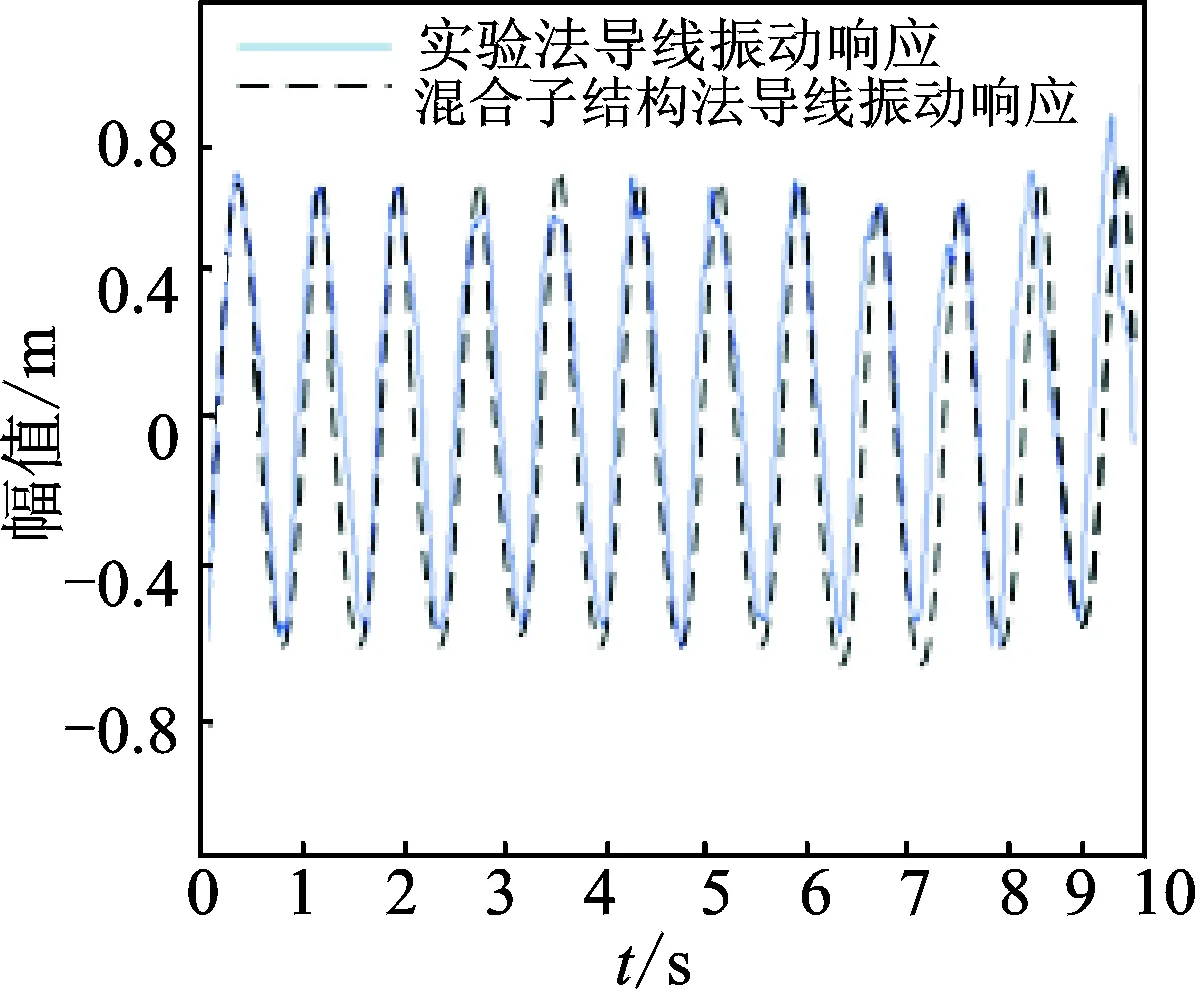
图18 输电导线横风振响应Fig.18 Cross-wind vibration response of the conductor

4 结 论

1) 通过自制输电导线风雨激振模拟实验装置，得到了具有典型倾角和雨线位置的输电导线在不同风速下的振动响应, 以及输电导线易发生风雨激振的风速大小和雨线的位置。

2) 利用混合子结构方法计算出输电导线发生风雨激振非定常气动力，并验证了上雨线引起输电导线气动力失稳是输电导线风雨激振的主要诱因。

3) 利用子结构方法得到的气动力计算出输电导线振动响应与实验结果接近，说明通过混合子结构方法得到的气动力具有较高的精度。该方法为不便于实验获取气动力系数的特性振动问题研究提供了一种有效途径。

4) 输电导线风雨激振机理非常复杂，采用CFD二维建模可能不能完全反应风雨激振的气动力特性。进一步研究需要建立三维理论模型和仿真模型求解振动时的气动力。

[1] Hardy C, Bourdon P. The influence of spacer dynamic properties in the control of bundle conductor motion[J]. Power Apparatus and Systems, IEEE Transactions on, 1980 (2): 790-799.

[2] Battista R C, Rodrigues R S, Pfeil M S. Dynamic behavior and stability of transmission line towers under wind force[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2003, 91(8): 1051-1067.

[3] Loredo-Souza A M, Davenport A G. A novel approach for wind tunnel modelling of transmission lines[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(11): 1017-1029.

[4] Loredo-Souza A M, Davenport A G. Wind tunnel aero elastic studies on the behavior of two parallel cables[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(4): 407-414.

[5] Li Hongnan, Tang Shunyong, Yi Tinghua. Wind-raininduced vibration test and analytical method of high-voltage transmission tower[J]. Structural Engineering and Mechanics, 2013, 48(4): 435-453.

[6] 李宏男, 任月明, 白海峰. 输电塔体系风雨激励的动力分析模型[J]. 中国电机工程学报, 2007, 27(30): 43-48.

Li Hongnan, Ren Yueming, Bai Haifeng. Rain-wind-induced dynamic model for transmission tower system[J] Proceedings of the CSEE, 2007, 27(30): 43-48.(in Chinese)

[7] Zhou Chao, Liu Yanping, Ma Zhiyong. Investigation on aerodynamic instability of high-voltage transmission lines under rain-wind condition[J]. Journal of Mechanical Science and Technology, 2015, 29(1): 131-139.

[8] Zhou Chao, Liu Yibing，Rui Xiaoming. Mechanism and characteristic of rain-induced vibration on high-voltage transmission line[J]. Journal of Mechanical Science and Technology, 2012, 26(8): 2505-2510.

[9] 周超, 芮晓明, 柳亦兵, 等. 输电线路风雨激振分析模型及数值分析[J]. 振动、测试与诊断, 2012, 32(3): 462-466.

Zhou Chao, Rui Xiaoming, Liu Yibing, et al. Analytical model and numerical analysis of rain-wind induced vibration on transmission line[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(3): 462-466.(in Chinese)

[10] 顾明, 李寿英, 杜晓庆. 斜拉桥拉索风雨激振理论模型和机理研究[J]. 空气动力学学报, 2007, 25(2): 169-174.

Gu Ming, Li Shouying, Du Xiaoqing. Investigation on mechanism and model of rain-wind induced vibration of cables[J]. Acta Aerodynamica Sinica, 2007, 25(2): 169-174.(in Chinese)

[11] Gu Ming, Du Xiaoqin. Experimental investigation of rain-windinduced vibration of cables in cable-stayed bridges and its mitigation[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2005, 93(1): 79-95.

[12] Zhou Chao, Liu Yanping, Song Yuwang. Mechanism and modeling of rain-wind induced in-plane vibration on high-voltage transmission line[J]. Journal of Mechanical Science and Technology, 2014，28(4): 1175-1180.

[13] 陈文礼, 李惠. 斜拉索风雨振-实验与数值模拟混合子结构方法[J]. 哈尔滨工业大学学报, 2011, 43(8): 6-10.

Chen Wenli, Li Hui. Aerodynamic characteristics of air-inflated membrane structure based on a hybrid substructure method[J]. Journal of Harbin Institute of Technology, 2011, 43(8): 6-10.(in Chinese)

[14] 陈文礼. 斜拉索风雨激振的实验研究与数值模拟[D]. 哈尔滨: 哈尔滨工业大学, 2009.

[15] Li Hui, Chen Wenli, Xu Feng, et al. A numerical and experimental hybrid approach for the investigation of aerodynamic forces on stay cables suffering from rain-wind induced vibration[J]. Journal of Fluids and Structures, 2010, 26(7): 1195-1215.