基于S变换的时域边际谱及其应用

潘宏侠， 李 肖， 李宗贤

(1.中北大学机械与动力工程学院 太原,030051) (2.长城汽车股份有限公司技术中心 保定,071000)(3.西北机电工程研究所 咸阳,712099)

引 言

对振动信号进行处理与分析作为监测机械设备运行状态的方法一直受到广泛关注，同时也是机械故障诊断技术的一个重要方向，利用采集到的振动信号提取关键的特征值是进行故障诊断十分有效的方法[1-2]。现实情况中得到的振动信号具有非平稳、非线性的特征。传统的信号处理方法在处理平稳信号时效果尚可，但在处理频谱随时间变化的非平稳信号时无法反映信号的局部时频特征，不能有效提取代表机械设备运行状态的特征值。因此提出一种适于处理非线性和非平稳信号的方法是十分有价值的课题。

为了更好地处理非线性、非平稳信号，文献[3-4]提出了一种自适应时频分析方法——Hilbert-Huang变换，其核心是经验模态分解(empirical mode decomposition，简称EMD)，把信号分解成一系列频率从高到低的本征模态函数(intrinsic mode function，简称IMF)，再利用Hilbert变换计算每个本征模态函数的瞬时频谱，把这些瞬时频率集合起来就得到了原始信号的时频谱。Hilbert-Huang方法能更好地反映非线性、非平稳信号的时频特征，也适用于分析线性和平稳信号。EMD方法是根据人的主观经验来进行信号分解，没有严格的数学基础，存在着端点效应、模态混叠、产生虚假模态以及没有收敛性的计算结果等缺陷。

笔者受Hilbert-Huang变换边际谱的启发，提出一种基于S变换的时域边际谱。首先，使用零空间追踪算法提取原始振动信号主要成分并消噪；其次，计算其S变换时域边际谱；最后，对时域边际谱做频谱分析，得到原始振动信号的主要特征频率。笔者通过仿真信号和齿轮箱振动信号的处理检验提出方法的有效性。

1 S变换及其时域边际谱

S变换(S transform，简称ST)是Stockwell等[5]提出的一种时频分析方法，在地球科学和电信号处理领域有广泛应用。S变换是基于可变窗口的短时傅里叶变换，又可以看作是小波变换的相位修正。信号x(t)的S变换[5-6]表示为

(1)

其中：f为频率；τ为时移参数；w为可变高斯窗。

(2)

S变换也可以从信号的频域角度表示为

f2)exp(j2πvτ)dv

(3)

其中：v为频移参数。

S变换作为基于特定基小波的小波变换，结合相位修正，就能够和经典的傅里叶变换联系在一起，所以S变换把短时傅里叶变换和小波变换结合了起来，具有两者的线性特征和可逆性的特点，且可以结合快速傅里叶变换进行相关运算，提高了计算效率，比较适合处理复杂信号。S变换作为一种时频分析方法，避免了短时傅里叶变换分辨率受海森堡测不准原理的约束，没有Wigner-Ville干扰项的产生和小波变换对基小波的依赖性。多分辨率、可逆性优点使S变换成为时频处理领域的优良方法[7]。

边际谱的概念来自于对Hilbert谱的进一步处理[8-9]，Hilbert谱也是一种时频谱描述方法，常与EMD方法结合使用来描述信号的振幅在时间-频率谱上的变化。Hilbert谱H(ω,t)其边际谱定义为

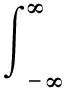
(4)

可见，Hilbert边际谱是描述幅值随频率变化的函数，其频率分辨率高于传统的傅里叶变换。基于类似的概念，也可以提出一种时域上的边际谱，对于Hilbert谱来说，其时域边际谱为

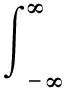
(5)

式(5)描述的是幅值随时间的变化规律。对于一个S变换时频描述函数S(ω,t)，其时域边际谱为

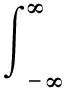
(6)

从ST时频谱图的角度考虑，S变换的时域边际谱实际上是所有幅值投影在幅值-时间平面的叠加除以信号的采样频率。在分析信号频率特征的情况下，为了方便计算，直接对所有幅值投影进行叠加，时域边际谱的频率特征基本不变。时域边际谱实际上是把信号能量随时间的变化通过时频变换的方法展现出来，与传统的时域-幅值或时域-能量表示不同，前者能够反映信号的局部时频及能量特征，更能体现信号的非平稳变化。

2 基于S变换时域边际谱的频率特征提取方法

在确立了S变换时域边际谱的概念后，可以引出基于S变换时域边际谱的故障特征提取方法。零空间追踪算法(null space pursuit，简称NSP)是近几年提出的信号分解算法[10]，在信号分解、处理非平稳信号以及消噪抗噪方面有很好的表现。首先，采用NSP算法分解信号进行消噪，提取故障信号中最能体现故障特征的信号成分；其次，利用S变换获取时域边际谱；最后，通过快速傅里叶变换得到特征频率，判断故障类别，其流程如图1所示。

图1 S变换时域边际谱处理方法流程图Fig.1 Marginal time spectrum of S transform processing flow chart

3 仿真研究

为了说明该方法的有效性，对仿真的故障滚动轴承振动信号进行处理。当滚动轴承发生常见的内圈、外圈或滚动体点蚀和磨损故障时，其振动信号会受到轴或保持架转频的调制作用，且其冲击能量持续时间短、衰减较快、调制幅值基本不变。根据这些特点模拟如下冲击信号

(7)

其中：轴承固有频率ωn=2πfn；fn=3 000 Hz；幅值常数y0=5；阻尼比ξ=0.1。

轴承发生故障时，冲击信号按照一定周期不断产生，因此定义为

(8)

且信号x(t)周期为T，使冲击信号间隔频率为100 Hz，即T=0.01 s，同时加入信噪比为7 dB的高斯白噪声。由于i越大，y(t+iT)的冲击能量就越小，这里选取n=20。信号采样频率为20 kHz，数据长度N=4 096。处理过程如图2所示。

从图2(f)看出，基于ST时域边际谱的处理方法能够明显地体现出故障轴承的冲击间隔频率100Hz，并有明显的2倍频和3倍频成分，是该方法本身特性；同时看到低频成分比高频成分要明显。对比图2(b)的快速傅里叶变换频谱，虽然能找到冲击间隔频率，但是与周围频率成分相比其幅值并不突出。

图2 仿真信号处理Fig.2 Simulated signal processing

根据仿真信号的分析可以看出，该方法会抑制信号的高频成分，突出低频特征频率，对信号中冲击能量成分比较敏感，能够提取具有一定能量冲击的微弱故障特征。对于齿轮箱来说，其振动信号中能量比较大的往往是各个轴的转频及其倍频、齿轮的啮合频率及其倍频等高频成分，如果不是很大的故障，想要提取故障特征频率就会受到这些成分的干扰，对于比较微弱的故障更是如此。因此，基于NSP分解和S变换时域边际谱的故障诊断方法为齿轮箱故障诊断提供了新的思路。

4 实验验证

为了验证本研究方法处理实际振动信号的应用价值，进行了齿轮箱故障诊断实验，如图3所示，并应用该方法进行信号处理和故障识别。选定起减速作用的齿轮箱作为故障设置对象，采用人工预先设定故障的方案[11]把齿轮箱的工作状态分为正常及滚动轴承保持架、滚动轴承滚动体和滚动轴承外圈故障4种。通过其他3种故障状态采集到的振动信号与正常状态对比来验证处理方法的有效性。所得振动信号以毫伏(mV)标定。

图3 齿轮箱传动系统总体结构Fig.3 The gearbox drive system

为了保证数据的可参考性和对比性，每种故障都设置在减速器的第2轴，即靠近输入轴的中间轴。图4为参考齿轮箱内部结构图。

图4 齿轮箱内部结构图Fig.4 Inner structure of gearbox

表1 滚动轴承的理论故障频率Tab.1 Theoretical fault frequency Hz

4.1 正常工况振动信号分析

篇幅所限，这里只给出原始信号和经本研究方法得到的时域边际谱及其快速傅里叶变换频谱，如图5所示。

图5 正常工况振动信号处理Fig.5 Signal under normal condition processing

在图5(c)可以看到，时域边际谱的频谱主要集中在低频段，利用时域边际谱的特点可以在处理故障信号时提取低频的特征频率。鉴于以上原因，这里主要关心100 Hz以下的频率成分。从图5(d)看到主要有0.6104，2.93，5.005，10.01和19.65 Hz频率成分，并没有出现某种故障的特征频率。其中，0.6104Hz为轴4的转频，2.93 Hz为轴3的转频，5.005和10.01 Hz分别为轴2的转频及倍频，19.65 Hz为轴1的转频在振动信号中的体现。可见，输出轴的转频最为明显，主要是因为经过时域边际谱的处理，信号的频谱更加突出其低频成分，且输出轴带动增速器和涡流制动器进行转动，运转时受到的强度很大。在工程实际中，制造误差、安装偏心和弹性变形是不可避免的，这增加了输出轴转频成分的能量体现，其他频率成分由于远离负载，能量相对较小。正常状态下的信号处理说明，本研究方法能够排除高频的干扰，分辨出频率很低的每个轴的单倍频，除了输出轴外，其他轴的转频可以作为提取故障频率的参考。

4.2 保存架故障振动信号分析

保持架故障振动信号处理过程如图6所示。从图6(c)可以看到，频率1.953 Hz的存在，其能量远大于其他3个轴的转频能量，与理论故障频率2.05 Hz非常接近，可以推断是保持架故障，与实验相符。

图6 保持架故障振动信号处理Fig.6 Signal under cage defect condition processing

4.3 滚动体故障振动信号分析

滚动体故障振动信号处理过程如图7所示。从图7(c)可以看到，与理论故障频率13.21 Hz相近的频率成分为13.18 Hz。虽然与3个轴的转频能量相差不大，但是后面又出现了能量较高的26.37和39.55 Hz频率成分，分别为13.18 Hz的二倍频和三倍频。

图7 滚动体故障振动信号处理Fig.7 Signal under rolling element defect condition processing

只有当滚动体的损伤部位接触滚道时，才会引起比较明显的冲击性振动且存在很大的能量衰减。考虑本次实验故障设置的比较轻微，滚动体故障的特征频率能量不是很大，因此可以确认为滚动体故障。

4.4 外圈故障振动信号分析

图8 外圈故障振动信号处理Fig.8 Signal under outer defect condition processing

外圈故障振动信号处理过程如图8所示。结合图8(c) 的快速傅里叶变换谱可以看到，存在特征频率33.69 Hz以及基于其二倍频和三倍频63.48和99.61 Hz。33.69 Hz与外圈理论故障频率32.86 Hz基本一致，可以确定为外圈磨损故障，与实验相符。可见，外圈故障的冲击能量最明显，保持架故障其次，滚动体故障冲击最不明显。结合故障设置情况，保持架为割裂故障，故障相对较严重，而滚动体只是被打磨一个小缺口，只有在滚动体凹坑部位与内外圈接触时冲击才明显，外圈虽然只是磨损，但磨损部位会持续影响轴承振动信号。因此，故障信号处理后的结果与实验情况相符。对滚动体微弱故障的成功诊断说明了该方法可用于对齿轮箱滚动轴承微弱故障的诊断。

5 结束语

笔者分析了Hilbert-Huang变换时频谱的边际谱，引出时域边际谱的概念，提出一种S变换的时域边际谱。利用基于S变换时域边际谱的频谱分析方法对仿真信号和实际的齿轮箱振动信号进行频谱分析。结果表明，该方法得到的频谱能够很好表征原始振动信号的频谱特征，可成功提取信号中的特征频率，尤其是含有各种冲击的特征频率。

[1] 赵志宏.基于振动信号的机械故障特征提取与诊断研究[D].北京：北京交通大学，2012.

[2] 潘宏侠,都衡,马春茂.局域波信息熵在高速自动机故障诊断中的应用[J].振动、测试与诊断,2015,35(6):1159-1164.

Pan Hongxia, Du Heng, Ma Chunmao. High-speed automaton fault diagnosis based on local wave and information entropy[J]. Journal of Vibration, Measurement & Diagnosis, 2015,35(6):1159-1164. (in Chinese)

[3] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and Hilbert spectrum for nonlinear and nonstationary time series analysis[J]. Proceedings of the Royal Society of London, Series A, 1998,454:903-995.

[4] Huang N E, Wu M L, Qu W D, et al. Hilbert-Huang transform and its applications[M]. Singapore: World Scientific, 2003:101-225.

[5] Stockwell R G, Mansinha L, Lowe R P, et al. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing, 1996,44(4):998-1001.

[6] Tan Yanghong, Sun Yichuang, Yin Xin. Analog fault diagnosis using S-transform preprocessor and a QNN classifier[J]. Measurement, 2013,46(7):2174-2183.

[7] 李巍华,林龙,单外平.基于广义S变换与双向2DPCA的轴承故障诊断[J].振动、测试与诊断,2015,35(3):499-506.

Li Weihua, Lin Long, Shan Waiping. Bearing fault diagnosis based on generalized S-transform and twe- directional 2DPCA[J]. Journal of Vibration, Measurement & Diagnosis, 2015,35(3):499-506. (in Chinese)

[8] 杨宇,于德介,程军圣.基于Hilbert边际谱的滚动轴承故障诊断方法[J].振动与冲击,2005,24(1):70-72.

Yang Yu, Yu Dejie, Cheng Junsheng. Roller bearing fault diagnosis based on Hilbert marginal spectrum[J]. Journal Vibration and Shock, 2005,24(1):70-72. (in Chinese)

[9] 李奕璠,刘建新,李忠继.基于Hilbert-Huang变换的列车车轮失圆故障诊断[J].振动、测试与诊断,2016,36(4):734-739.

Li Yifan, Liu Jianxin, Li Zhongji. The fault diagnosis method of railway out-of-round wheels using Hilbert- Huang transform[J]. Journal of Vibration, Measurement & Diagnosis, 2016,36(4):734-739. (in Chinese)

[10] Peng S, Hwang W L. Null space pursuit: an operator- based approach to adaptive signal separation[J]. IEEE Transactions on Signal Processing, 2010,58(5):2475-2483.

[11] 潘宏侠,张翔.基于GAMP和EEMD的滚动轴承故障诊断研究[J].振动与冲击,2016,35(20):200-206.

Pan Hongxia, Zhang Xiang. Rolling bearing fault diagnosis based on GAMP and EEMD[J]. Journal Vibration and Shock, 2016,35(20):200-206. (in Chinese)