改进多目标粒子群算法的火箭布雷弹弹道求解方法*

潘军军，冯 柯，李焕良，杨小强

（解放军理工大学野战工程学院，南京 210007）

0 引言

某型火箭布雷车是一种可远距离布设防坦克雷场、防步兵雷场及混合雷场新型装备［1］。由于火箭布雷车是以火箭炮为基础改造而成，故现有火箭布雷车的布雷弹外弹道轨迹计算;方法主要参考自行式多管火箭炮的弹道轨迹；其射击诸元解算是通过拟合火箭炮射表的多项式来求解。这导致了无论是诸元精确度还是准确度都远远不能满足布雷场精确控制的作战需求。因此，找到一种可靠的布雷弹弹道解算方法显得尤为重要。

目前，火箭炮的外弹道模型的研究比较成熟，但是对于火箭布雷弹运动轨迹的研究却相对较少。文献［2］提出了火箭布雷弹空中散布及数值解，分析了火箭布雷弹在空中状态，但是对于布雷弹空中二次开舱后地雷运动轨迹缺少分析，难以科学地解算火箭布雷车实际布雷的运动轨迹，文献［3］在布雷外弹道学中利用近似解析公式法，通过简化计算或估算，能够快速得到结果，但准确性得不到保证。本文针对布雷弹在空中3个阶段建立运动方程，利用自适应步长的龙格库塔法进行数值求解，通过控制步长来保证求解精度。

对射击诸元的求解方法主要有2种：射表逼近法与数值积分发。由于射表逼近法的局限性，文献［4］将RBF网络应用于弹道解算中，但是神经网络的前期训练需要大量的数据，并不具有普适性；文献［5］提出了基于改进遗传算法的最佳射角反解模型，但该模型是针对火炮射程单目标优化问题，难以解决多目标问题；文献［6］提出了基于多目标粒子群算法解决了多目标优化问题，但初值敏感性强，局部搜索能力较差。本文针对布雷弹弹道射击诸元解算中多目标优化的问题，提出了一种改进的多目标粒子群优化算法。考虑到射击诸元的多样性与收敛性，将粒子群更新公式进行改进，同时引入了角度聚类的思想进行外部种群维护，得到了符合要求的满意解。

1 外弹道模型求解

1.1 外弹道模型

火箭布雷弹发射后在空中飞行，达到预定的时间时，抛射机构作用，将雷簇沿弹轴方向向前抛出，在分离机构的强制作用下，地雷相互迅速分离，受到雷伞的作用而减速，运动方向也逐渐改变，趋于垂直地面，进而落在地面，形成一定面积的地雷场［3］。布雷弹及雷伞系统在空中轨迹如图1所示。抛射过程经历的时间极短，为方便计算，雷簇脱离雷舱点p可认为与点op重合。根据上述运动原理可将布雷弹在空气中运动分为3个阶段。

第一阶段为火箭布雷弹从发射出定向管后到火箭发动机火药燃烧完，称为主动段，在标准气象条件下，假设布雷弹的攻角为零，该阶段火箭布雷弹的质心运动方程为［2］：

初始条件为 t=0 时，x=0，y=0，v=v0，θ=θ0。

第二阶段为主动段末端到布雷弹开舱点，称为被动段，这一过程弹道模型研究类似于普通布雷弹的弹道研究，此段火箭布雷弹的质心运动方程为［7］：

初始条件为 t=tK时，x=xK，y=yK，v=vK，θ=θK。

第三阶段为可撒布雷簇脱离雷舱瞬间到雷伞系统着地，由于采用了降落伞减速装置，伞张开后阻力增大，加之气动力特性及降落伞增阻过程的复杂性，将雷伞作为一个整体，进行外弹道模型研究，此段雷伞系统的质心运动方程为［8］：

其中：ρ、Cx0分别为空气密度和阻力系数，m、A分别为雷伞系统质量和最大横截面面积。

初始条件为t=tp时，其中vep为抛射机构抛射速度。

1.2 基于自适应步长的R-K法弹道模型求解

针对上述的火箭布雷弹外弹道模型，已知初速度、推力加速度等初始条件，再选定布雷弹高低射角和开舱时间，虽然利用文献［2］中的四阶R-K数值解法能够较简单地对模型进行数值求解，从而能够得到一条弹道轨迹。但是该轨迹曲线是由一些空间不连续的点连接而成的，很难得到终点y=0时的弹道诸元，对后面的优化算法必定会造成影响［5］。所以本文采用自适应步长的龙格库塔数值解法，由一个5级4阶和一个6级5阶R-K公式组成，可以用来改进解和监测精度［9］，并通过局部截断误差来控制步长，以保证精确的解算出地雷落点诸元。这样会导致整个模型求解过程比较长，但是得到的结果相对误差较小，大大提高了精度。

2 基于改进的多目标粒子群算法的射击诸元求解模型

多目标粒子群算法相对于其他算法具有原理简单，编程容易实现等特点［10］，但是基本的多目标粒子群算法存在种群初值敏感，难以保证解良好多样性和收敛性，而且在处理复杂多目标优化问题时容易陷入局部最优，因此，本文针对火箭布雷弹弹道射击诸元解算中多目标优化的问题，提出了一种改进的多目标粒子群优化算法。

2.1 Kent映射

由于多目标粒子群算法的初值敏感性，当初始种群在空间中分布越均匀，搜索的效果越好，得到的解集具有良好多样性和收敛性的概率也就越大。本文采用Kent混沌映射［11］对初始种群进行赋值，Kent混沌映射公式如下：

其中：x为混沌序列；β为设置参数。

当解 X 的取值范围为［xmin，xmax］，采用 Kent映射产生随机数r∈（0，1），利用下式进行种群初始化：

2.2 改进粒子群更新公式

基本粒子更新公式如下：

为了使具有良好多样性的粒子和良好收敛性的粒子引导整个种群，使得每个粒子都同时收到具有良好多样性粒子的引导和具有良好收敛性粒子的引导，对粒子群更新公式进行如下改进：

其中：c3，r3为权重系数；为具有良好收敛性的外部粒子为具有良好多样性的外部粒子。

采用文献［12］中的外部种群收敛性与多样性判别准则。从外部种群中选取两个非劣解集，操作步骤如下：

1）计算所在扇形区域中的非劣解与原点的欧氏距离Li，以及与所在扇形区域夹角φ，i为非劣解个数；

2）对Li和φ分别采用轮盘赌的方法选取非劣解作为。

2.3 外部种群维护

维护外部种群的主要目的是为了群体新的演化提供多样化的gbest。文献［13］采用聚类思想的方法保证了外部种群的分布多样性与均匀性。为了维护种群多样性，当外部种群非劣解的数量多余规定的上限时，在粒子数最多的扇形区域中，通过对所选择区域中非劣解采用多样性指标进行K均值聚类分析［13］，从所包含非劣解最多的类别中删去多余的非劣解，维护外部种群数量。

以多样性为标准对非劣解进行聚类分析，保证外部粒子群在每个方向上都分布有非劣解，能更好地引导粒子群进行全局最优搜索。

改进的多目标粒子群算法流程如下：

3 案例分析

根据现有资料，以某型布雷装备为例，已知目标射程，对最佳射击诸元进行求解，射击的初始条件如下页表1所示。

3.1 火箭布雷弹外弹道模型仿真

基于文中前面的火箭布雷弹外弹道模型，调用Matlab内置ode45函数程序对其进行仿真实验，得到仿真结果如下页图3所示。

图3（a）中曲线，火箭布雷弹弹道轨迹并非是标准的抛物线轨迹。从图中可以看出，弹道降弧段所占整个飞行距离的比例比升弧段小，这符合火箭布雷弹空气弹道的一般特性。从图3（c）中曲线可以看出，速度从初始点很快达到最大值，这段对应火箭布雷弹主动段。随后速度减小至开舱点，而后速度急速下降，这是由于降落伞打开，阻力变大。最后速度趋于稳定。由于重力作用，布雷弹倾角曲线由初始值开始变小，变成0°后又开始变大，最终达到最大值而稳定，如图3（b）所示。图中速度和加速度曲线在50 s时发生突变，是因为布雷弹在空中开舱后抛射机构在一瞬间给予地雷一个抛射速度。这与前面分析的弹道特性相一致，符合火箭布雷弹运动规律。

表1 射击初始条件

3.2 射击诸元求解模型仿真

火箭布雷车进行布雷作业时，火力点和目标点的位置是确定的，在射程误差范围内优化射角和开舱时间使得地雷落点诸元达到最优。该问题的数学模型如下：

其中：vc为地雷落点瞬时速度，θc为地雷落点瞬时角度，Xc为布雷弹射程，C为目标实际距离，ε为事先定义的精度。

由于该问题属于事先求解过程，所以不需要计算时间尽量短，而是需要尽可能找到全局的符合要求的精华解，避免了早熟现象。选取粒子个数为200，迭代3 000步，对该数学模型进行计算得到如下结果，如表2和图4所示。

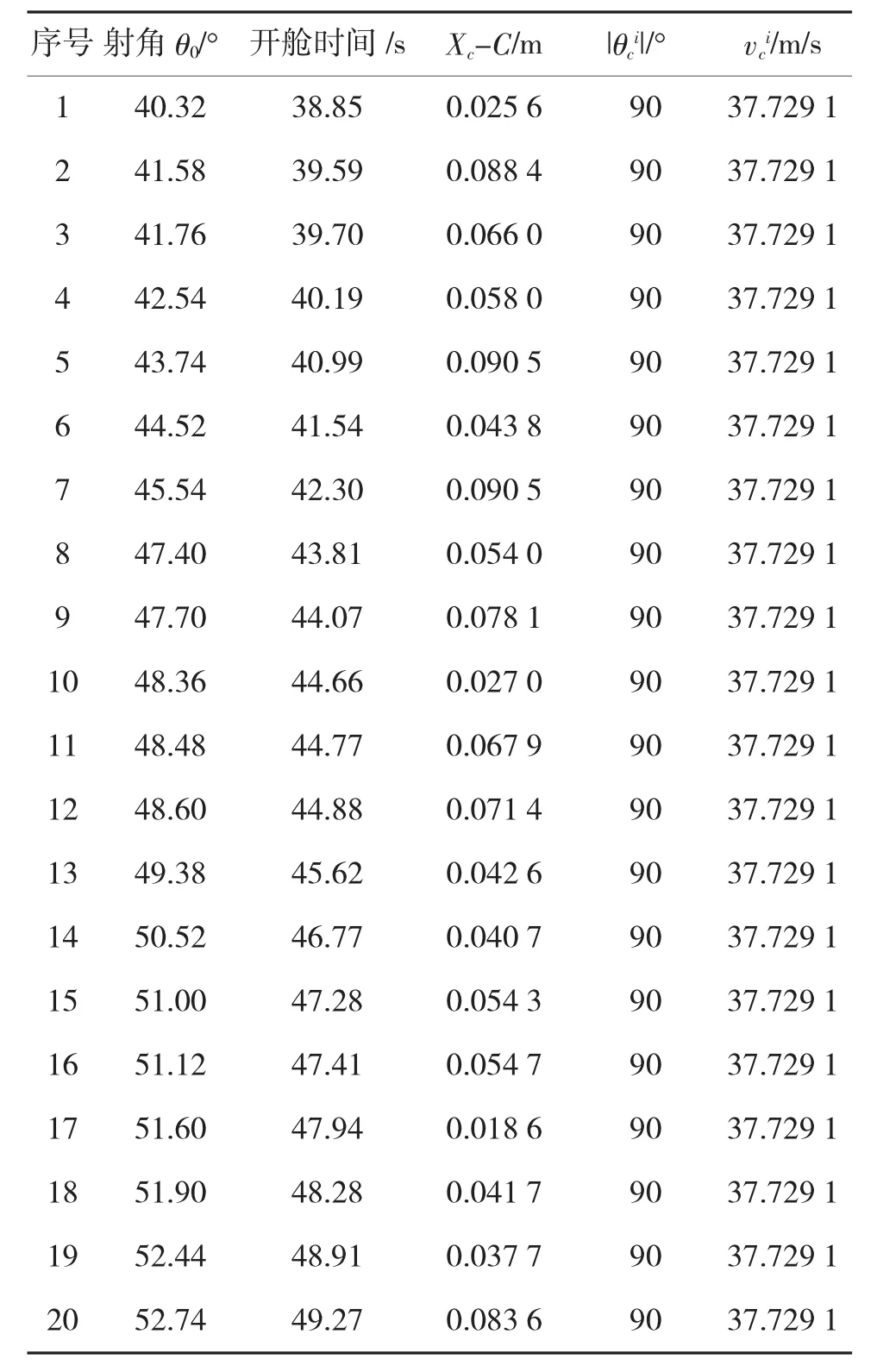
表2 非劣解集

表2为在射角和开舱时间取值范围内找出所有符合要求的非劣解集，从表中可以看出地雷着陆速度都是达到最小值，地雷着陆角都达到最大值，使得落点诸元达到最优，图4为符合要求非劣解集在空间分布情况。即对于某一确定目标点射程存在着多组射角与开舱时间的解能够满足作战需求，决策者可以根据火力点实际情况来选择某一射击诸元。

针对不同的目标射程，根据射击诸元求解模型求出的解进行靶场射击试验，由于考虑安全性，靶场布雷试验的布雷弹采用的是真弹假雷，其射击参数都是按照真实数据设计的，在无风无雨的天气条件下，进行靶场射击试验，得到结果如表3所示。

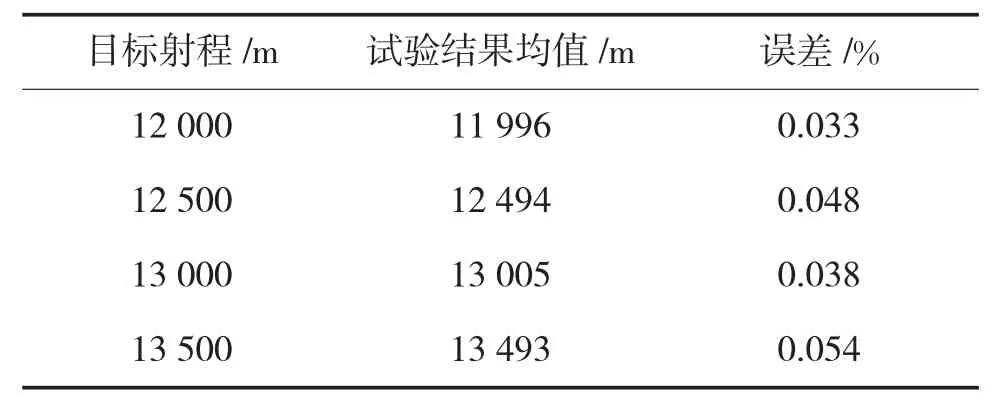
表3 靶场试验结果

通过分析试验结果，相对误差小于0.06%，满足射击条件，从而验证了本文弹道模型及射击诸元求解算法的有效性。

4 结论

本文选择了自适应步长的龙格库塔法的火箭布雷弹弹道模型，基于改进的多目标粒子群算法，以布雷弹落点速度、角度和射程为优化目标，针对某布雷装备进行仿真求解，得到了符合要求的满意解。1）该方法建立了合理的布雷弹外弹道模型，保证了弹道的精度与准确度；2）该方法利用改进的多目标粒子群算法得到一个可行解集，为火箭布雷装备的射击诸元的求解提供可靠的方法；3）该方法是一种通用的射击诸元解算方法，针对不同的模型，合理的改变参数即可。

［1］郭铭.新军事变革条件下的武器装备采办项目风险管理研究［D］.北京：北京邮电大学，2009.

［2］刘炳琪，吴强.火箭布雷弹的空中散布及数值解［J］.数学理论与应用，2001，21（1）：126-128.

［3］刘松培.布雷外弹道学［M］.北京：兵器工业出版社，1999.

［4］吕强，李建勋，周启煌.RBF网络用于战车火控系统弹道解算的方法［J］.火力与指挥控制，2007，32（4）：26-28.

［5］刘彦君.基于改进的遗传算法与龙格库塔法的弹道求解方法［J］.兵工自动化，2011，30（1）：4-7.

［6］伍思敏，陈珺，刘飞.基于多目标粒子群的非线性系统PID 控制器设计［J］.计算机工程与应用，2014，50（23）：69-72.

［7］徐明友.火箭外弹道学［M］.哈尔滨：哈尔滨工业大学出版社，2004.

［8］张珂.子母弹抛撒技术研究［D］.南京：南京理工大学，2012.

［9］孙幸福，狄邦达.高炮火控外弹道实时解算及其应用［J］.火力与指挥控制，2007，32（5）：110-112.

［10］雷德明，严新平.多目标智能优化算法及其应用［M］.北京：科学出版社，2009.

［11］陈增强，周茜，袁著祉.基于Kent映射的数字喷泉编解码 方 法 研 究 ［J］.系 统 科 学 与 数 学 ，2011，31（6）：731-741.

［12］刘宝宁，章卫国，李广文，等.一种改进的多目标粒子群优化算法 ［J］.北京航空航天大学学报，2013，39（4）：458-462.

［13］刘丽琴，张学良，谢黎明，等.基于动态聚集距离的多目标粒子群优化算法及应用［J］.农业机械学报，2010，43（3）：189-194.