基于卫星无源探测的飞行器主动段轨道估计*

陈江波，刘培学，曹爱霞，高 颖

（1.青岛黄海学院机电工程学院，山东 青岛 266427；2.烟台大学光电信息科学技术学院，山东 烟台 361005）

0 引言

随着科学的发展，卫星探测技术已步入一个新的阶段［1］。传统的有源探测存在一些缺陷，阻碍了它的发展，针对这些问题，需不断寻求新的卫星探测技术，提高卫星探测工作能力和工作效率，从而使其有广阔的应用。因而，无源探测工作方式越来越受到各国的广泛重视［2］。

要推断空间飞行器的轨道参数，需用观测的数据来建立数学模型，再匹配相应的计算方法来实现［3］。无源定位是实现目标探测的一项关键技术，目前，该技术不断得到完善，拥有广阔的应用前景。所谓无源定位，就是在不向目标发射电磁波的条件下，通过测量雷达、通信等发射机（辐射源）的，即可化为下列一阶微分电磁波参数或测量目标的可见光和红外参数来获取辐射源及其携载平台或目标位置的一种定位方法［4］。通过该定义，可以知道无源定位系统不仅隐蔽性好、作用距离远，而且生存能力强。一般空间飞行器的飞行历经主动段、自由段和再入段，自由段和再入段合称为被动段。虽然主动段时间不长，但是火箭发动机尾焰的红外辐射很强，能够被预警卫星红外传感器探测到。因此，对于主动段的建模和估计是头等大事［5］。

1 运动方程以及研究问题

在基础坐标系下，由变质量质点的动力学可知，空间飞行器主动段的简化运动方程可表示为：

在式（1）中，如果只保留式中的第一项，则简化运动方程为：

在观测坐标系下，使用两个无量纲比值来确定化简后得到的空间飞行器的观测数据，如下所示：

观测的数据具有不准确性，会存在误差。根据工程经验，通过将模型进行相应的简化，可以将存在的系统误差分解为影响较弱的原点位置误差和影响较大的三轴指向误差。只要尽可能减小三轴指向误差便可以极大提高观测数据的准确性，在这里将其分解为一个旋转误差和两个平移误差［7-8］。

现在忽略系统误差的影响，在仅考虑随机误差的情况下，研究以下问题：

1）在任意时刻观测卫星的位置计算是估计的前提，根据第九届全国研究生数学建模竞赛B题中给出的数据satinfo.txt和上述观测卫星的简化运动方程式（2），计算题目中09号观测卫星在50.0 s、100.0 s、150.0 s、200.0 s、250.0 s 5 个时刻的三维位置。satinfo.txt中包含了卫星在初始时刻对地的高度、速率等，可以认为是卫星实际运行数据。

2）在竞赛过程中给定所需的仿真数据下，06号和09号观测卫星对0号空间飞行器形成了立体交叠观测，按照逐点交汇定位的思路，给出0号空间飞行器在式（1）框架下的轨道估计。

2 解决方案及结果

2.1 问题1解决方案

考虑采用常微分方程初值问题数值解法来求取 09 号观测卫星在 50.0 s、100.0 s、150.0 s、200.0 s、250.0 s 5个时刻的三维位置［9］。由于观测卫星的简化运动式（2）是一个二阶微分方程，因此，可以选择运用龙格-库塔公式计算数值解。

对于二阶微分方程的初值问题：

针对这个问题应用四阶龙格--库塔公式

其中，

带入式（5）整理可得

09号观测卫星在基础坐标系下的初始位置和速度数据见表1所示。

表1 09号观测卫星在基础坐标系下的初始位置和速度

利用Matlab软件对式（2）进行数值计算，得到09 号观测卫星在 50.0 s、100.0 s、150.0 s、200.0 s、250.0 s 5个时刻的三维位置坐标，见表2所示。

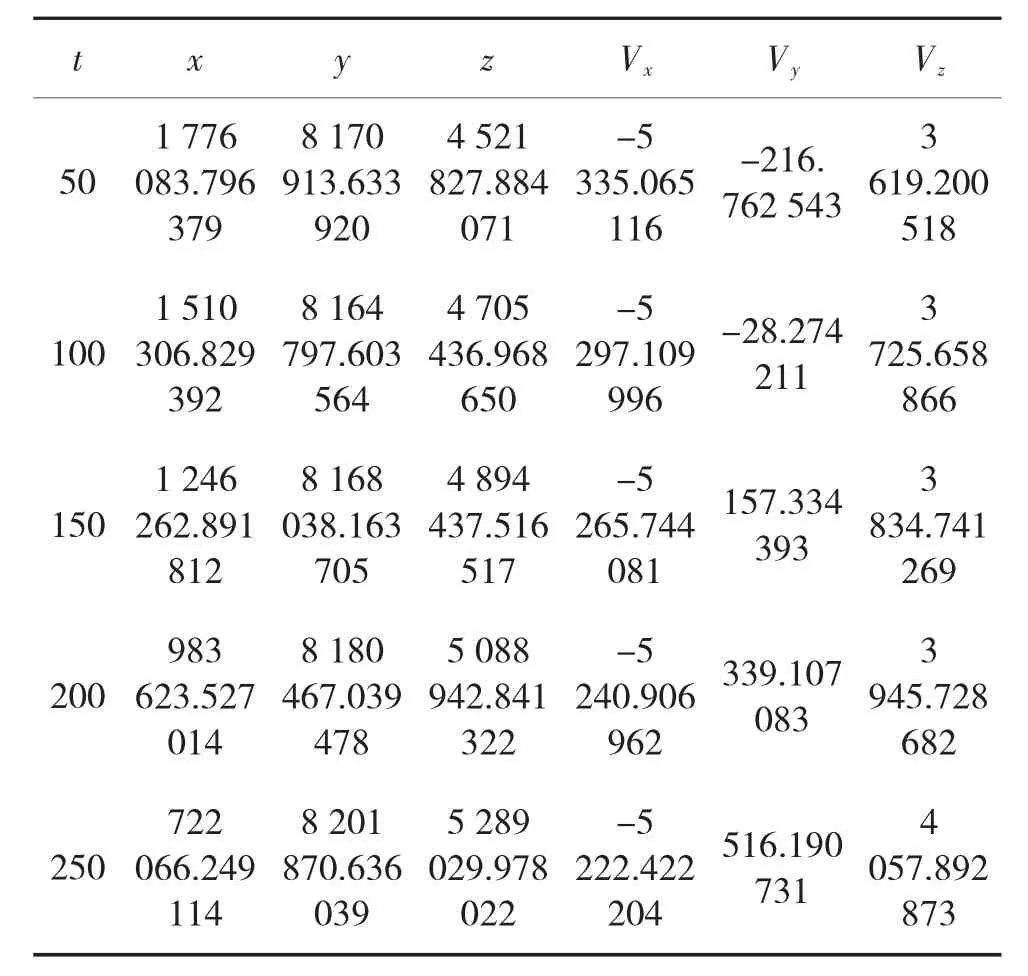
表2 09号观测卫星在5个时刻的三维位置坐标

2.2 问题2解决方案

首先，选取基础坐标系，本文选取随地心平移的坐标系，其次，原点选取地球中心Oc，z轴选取地球的自转轴，这里取指向北极的方向作为z轴的正方向，选取由Oc指向零时刻的0经度线作为x轴，y轴是按照右手系最终确定，由选取的x轴，y轴，z轴，原点Oc建立直角坐标系。地心Oc围绕着太阳椭圆轨道进行运动，因此，在理论上直角坐标系系不是惯性系。由于空间飞行器的观测弧段时长远小于地球公转周期，因此，这里在较短时间内可以将该直角坐标系看作是惯性系，值得注意的是基础坐标系是不随地球运动的［10］。

第2个坐标系是随卫星运动的观测坐标系Os-XsYsZs，见图1，选取卫星中心Os作为原点，选取OcOs所在直线作为Xs轴，这里取远离地球方向作为Xs轴的正方向，选取垂直Xs轴为Zs轴，其方向指向正北，Ys轴也是根据右手系来确定。

首先，应用3次样条插值将修正后的06号、09号观测卫星对0号空间飞行器在各自观测坐标系下的各个离散数据点拟合成一条连续的曲线，从而能近似得到每个时刻的α和β值，进而将时间进行统一［11-12］，见表 3、表 4 所示。

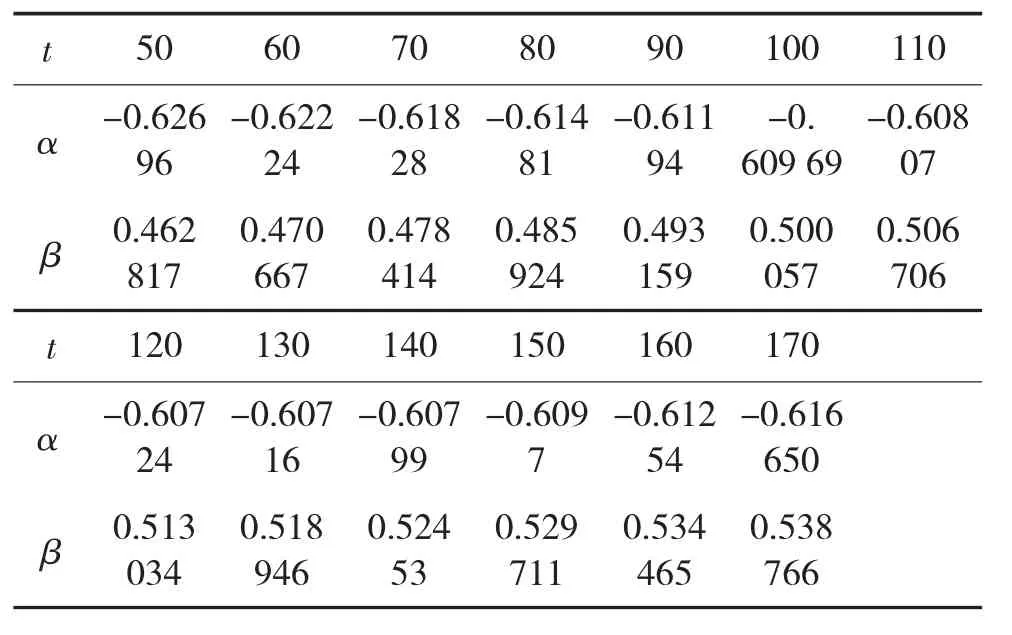
表4 09号观测卫星对0号空间飞行器在采样点近似数据

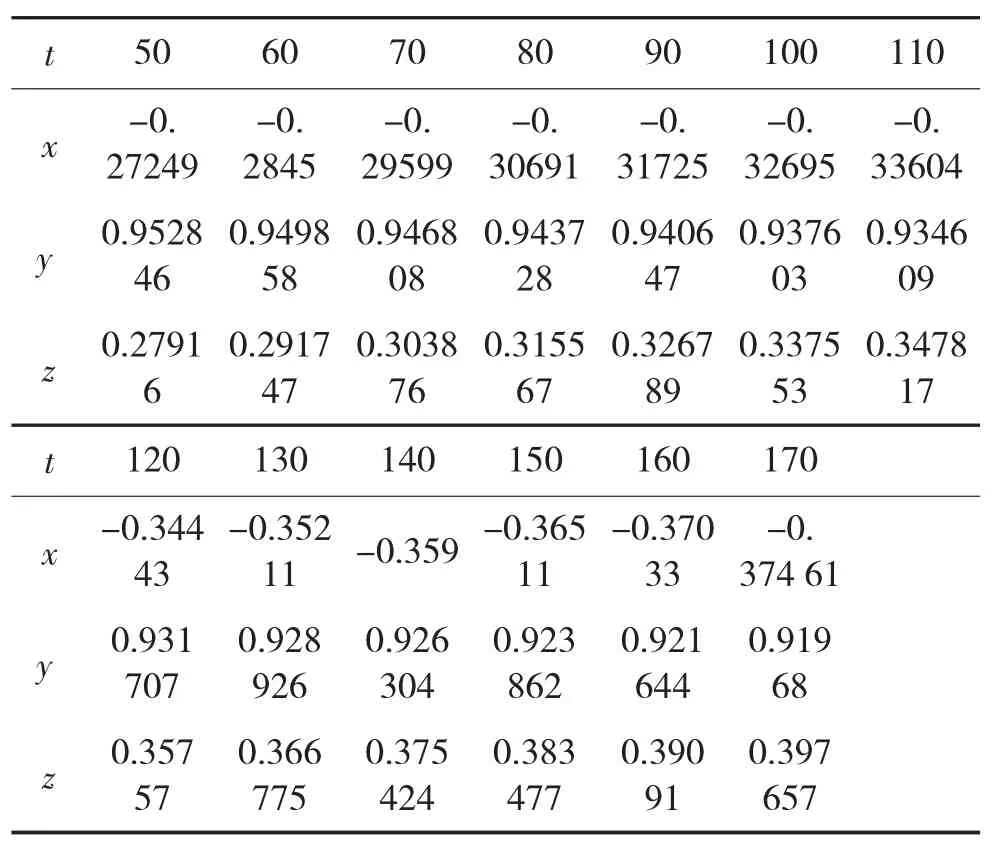
表5 0号空间飞行器相对于06号观测卫星各个采样点在基础坐标系下的方向向量

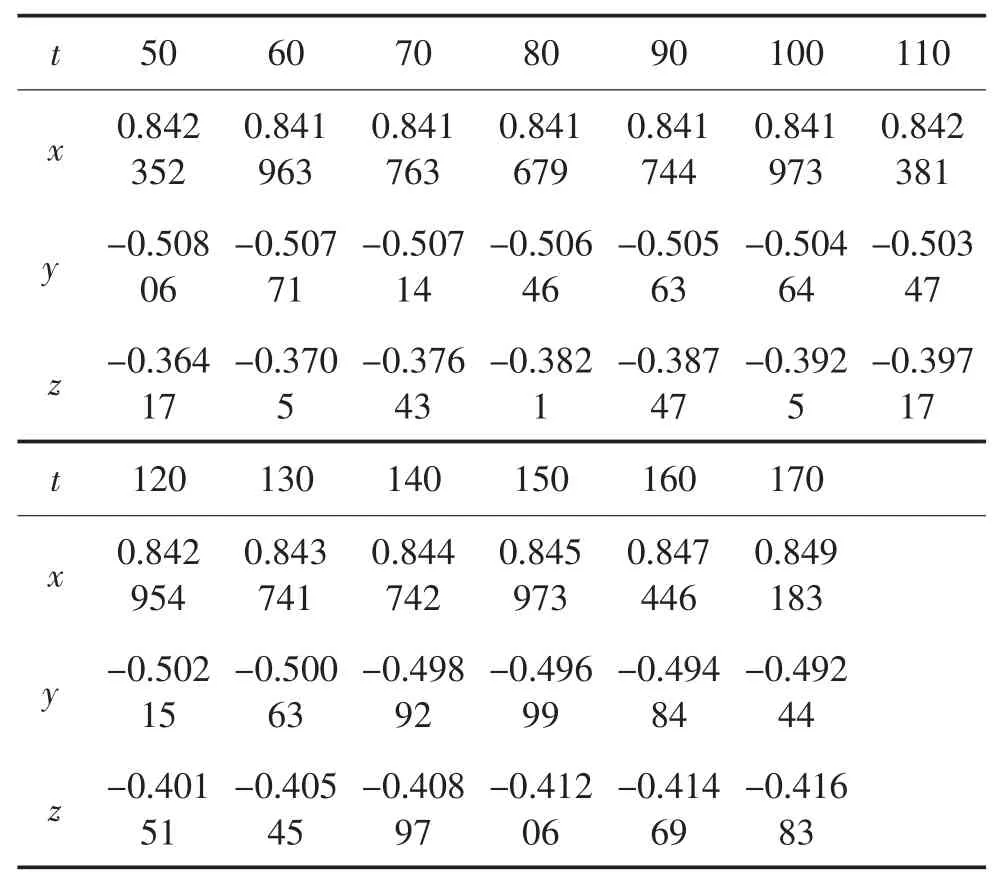
表6 0号空间飞行器相对于09号观测卫星各个采样点在基础坐标系下的方向向量

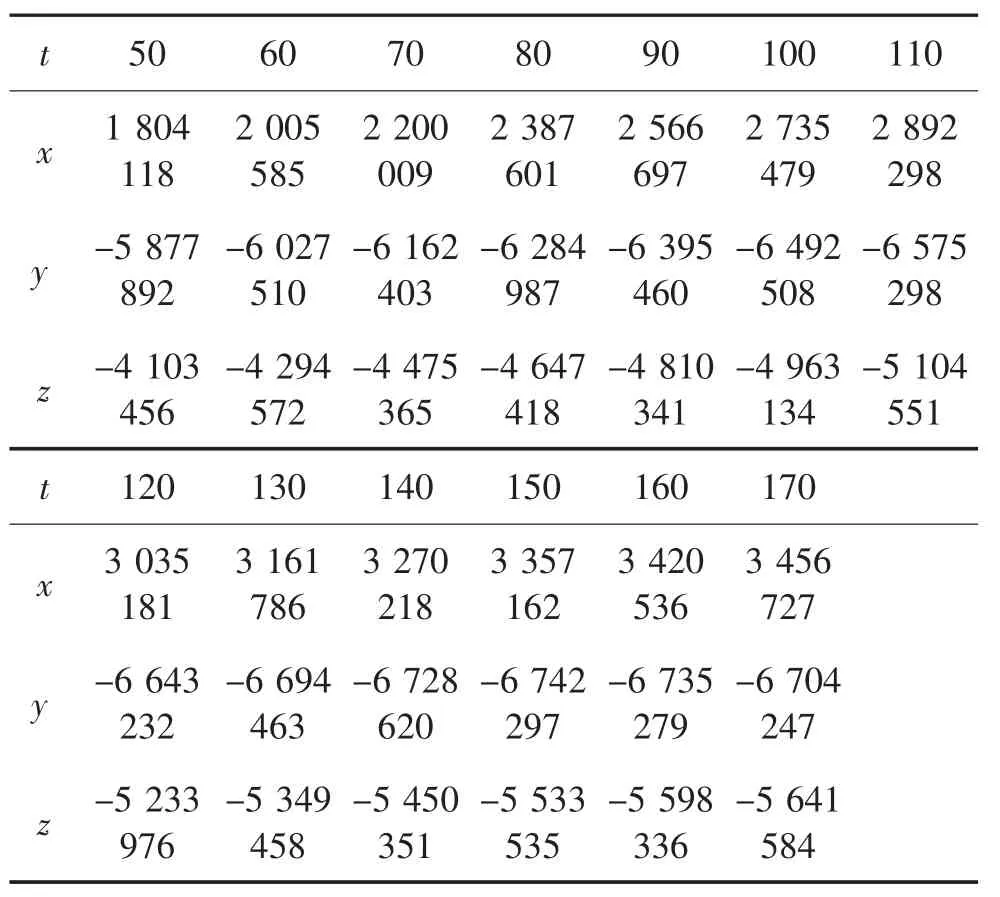
表7 0号空间飞行器在基础坐标系下的三维坐标

其次，设方位角为a，俯仰角为e，见图2，则

0号空间飞行器在06号、09号观测卫星坐标系下的单位向量为：

基础坐标系与观测坐标系间的转换矩阵式

最后，从50.0 s到170.0 s每间隔10.0 s对空间飞行器在06号和09号卫星观测坐标系下的修正数据进行采样，利用上述公式应用MATLAB软件，分别计算得出0号空间飞行器相对于06号观测卫星、09号观测卫星的各个采样点在基础坐标系下的方向向量，见表5、表6所示。

观测卫星逐点交汇定位飞行器即为同一时刻两颗以上的卫星关于同一个目标的视线相交，利用最小二乘法的原理解决超定方程，近似得出空间飞行器在基础坐标系下的三维坐标，见表7所示。

此式对任意时刻t的x，y，z均成立，于是化简为：

解得

选取适当基底，应用Mathematica软件进行最小二乘拟合，得出空间飞行器在基础坐标系下的位置函数及轨迹，见图3、图4所示。

最后进行残差估计。通过空间飞行器在基础坐标系下所拟合的轨迹方程每间隔10.0 s求得其从50.0 s到170.0 s的13个坐标，见表8所示。

表8 0号空间飞行器在拟合轨迹中采样点的三维坐标

其中残差为观测值与预测值（拟合值）之间的差的平方平方值（样本标准差）。通过本文算法，所得到的残差见表9所示。

表9 残差估计值

3 结论

关于卫星无源探测空间飞行器主动段轨道估计与误差分析是一个庞大的、繁琐复杂的问题，本文针对其中的一部分内容进行了研究，应用多种工具软件进行数值计算和估计，使其得到的结果更为精确，估算出空间飞行器在基础坐标系下主动段的简化运动方程，求解方程，由解的形式可选取适当方法拟合0号空间飞行器的轨道方程，并估计残差，通过残差的对比，发现本文方法的精度高、可信度强。但是本文没有确定的具体表达式，仅给出其通式，确定的具体表达式将是本文下一步的研究方向。

［1］刘莹.基于北斗卫星的无源雷达定位方法研究［D］.新乡：河南师范大学，2013.

［2］黄伟，徐建城，吴华兴.弹载SAR末制导段轨迹控制算法［J］.系统工程与电子技术，2016，38（9）：2115-2121.

［3］刘科，郭小和，周继强.基于卫星无源探测的空间飞行器轨道估计［J］.电光与控制，2014，21（5）：97-103.

［4］胡磊，刘辉，闫世强，等.导弹预警卫星对助推段导弹的探测能力建模［J］.火力与指挥控制，2015，40（1）：174-177.

［5］张雨，贺婷婷，郭建广，等.基于卫星无源探测的空间飞行器主动段轨道估计与误差分析［J］.数学的实践与认识，2013，43（14）：187-196.

［6］漆亚龙，李汇军，项杰，等.低轨航天器弹道系数估算及热层大气模型误差分析［J］.空间科学学报，2014，34（1）：89-94.

［7］EMMERT J T.A long-term data set of globally averaged thermospheric total mass density［J］.J.Geophys.Res，2009，114，A06315，doi：10.1029/2009JA014102.

［8］全杰.弹道导弹目标威胁评估模型和算法［J］.现代防御技术，2014，42（4）：24-30.

［9］李晓宇，田康生，郑玉军，等.单星观测下弹道导弹状态估计与预测误差分析［J］.火力与指挥控制，2015，40（8）：5-8.

［10］张丽艳，杜忠华，张志安，等.一维弹道修正弹分段解算控制算法的研究［J］.火力与指挥控制，2015，40（8）：143-145.

［11］KOPPENWALLNER G.Satellite aerodynamics and determinati-on of thermospheric density and wind［J］.AIP Conf.Proc.，2011，1333：1307-1312.

［12］EMMERT J T，LEAN J L，PICNE J M.Recordlow thermospheric density during the 2008 solar minimum ［J］.Geophys.Res.Lett.，2010（37）：L12102.