浅谈培养学生审题能力的策略

李美云

[摘 要]审题是解题过程中的关键环节，也是解决问题的基础和先导，培养学生的审题能力是数学教学的重要内容。在教学中，教师应调动学生的多种感官，从听、说、读、写等方面教会学生正确的审题方法，培养学生认真、严谨的审题习惯。

[关键词]读；说；画；审题方法；审题习惯

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2018）02-0080-02

学生的作业是课堂教学的一面“镜子”，是师生交流信息的“窗口”。作业反映了学生对知识的理解与掌握情况，教师可以通过学生完成作业的情况，了解学生对基础知识和基本技能的掌握程度，了解学生的学习水平和存在的问题。教师还可以通过作业反映出来的问题进行总结与反思，从而及时调整和改进教学内容、教学方式，提高教学效率。学生完成作业的质量与态度也是家校交流的主要话题，很多家长反映：“对于孩子作业中的错题，我们看了很吃惊，都是一些很低级的错误，孩子太粗心了……”这样的遗憾在每个年级、每个班级的每次作业中均有存在。

其实，粗心、马虎暴露的是学生理解能力和审题能力薄弱的问题。审题能力是一种获取信息、分析信息和处理信息的能力，它以一定的知识水平为基础，以良好的读题习惯、有效的思考方法为保证。为培养学生的审题能力，我从以下三方面着手。

一、读一读，想一想

读题是培养审题能力的第一步。通过读题，学生初步理解题意，为进一步思考、分析、作答做准备。教师在教学中要根据学生的年龄特点，对读题形式和要求做出明确的规定。

教学一年级的学习内容时，由于一年级学生年龄小，识字量少，读题有一定的困难，教师应注意有目的地引导学生读题，找出关键词，正确理解题意后再解答。引导学生读题有以下几种方法。

1.范读。教师读题，要求学生听题时左手指着题目，右手拿笔随时准备书写。教师读题时速度要尽可能慢，留给学生思考的时间。

例如，教学“确认位置”时，题目中出现了“前、后、左、右、上、下”这些方位词，它们是答题的关键。一些有超前意识的家长在学生进入小学前就教学生识字，这样的学生理解题目就相对容易，但对于大多数刚入学的学生来说，许多字还都很陌生，教师应当先示范读题，再带领学生认读，并在读懂题意后再答题。

2.跟读。随着学生知识的不断积累，教师可让学生小声地跟教师一起读题，细读、慢读，逐步理解题意。

3.精读。教师带领学生读题时，要注意对题目中的关键词使用不同的语气，让学生易于领悟。

例如，教学“几和第几”时，有这样一道题：

☆ ☆ ☆ ☆ ☆

（1）从左边起，圈出4个☆。

（2）从右边起，给第4个☆涂上颜色。

教师读题时可以通过语气强弱的变换，暗示学生要注意左右，并思考左边第4个与右边第4个的区别。经过几次训练，学生遇到此类题目时，就会找准解题关键词了。这样教学生读题，可以培养学生的审题能力，使学生作业正确率有所提高。

二、看一看，说一说

学生观察事物的过程自始至终地伴随着思维活动。低年级教材中的题目多数图文并茂，这就要求学生具备一定的观察能力和語言表达能力。

审题时能否准确理解词义是解题的关键。教师必须有意识地引导学生学会用心观察，学会用自己的语言准确地概括题意，进而提高分析能力。

例如，教学“6、7的分与合”时，教师在学生观察螃蟹图后这样引导。

师：一只只张牙舞爪的大螃蟹想和我们比赛。大家看，它们争先恐后地出题考我们，大家有没有信心战胜它们？

生（齐）：有。

师：知己知彼，方能百战百胜。谁能说出一只大螃蟹身上的数字6和两只小螃蟹身上的数字1、5有什么关系？

生1：6可以分成1和5。

生2：6可以分成5和1。

生3：1和5、5和1，合起来都是6。

师：下面谁来替第二只螃蟹出题？

生4：哪个数可以分成4和3？

生5：你的问题可以换成4和3合起来是几。

教师通过生动有趣的语言、激励的语气，先引导学生观察配图，厘清题目中蕴含的数量关系，不仅调动了学生学习的积极性，还培养了学生的语言表达能力。

三、圈一圈，画一画

教育家叶圣陶先生说过：“什么是教育，简单一句话，就是培养良好的习惯。”到了中高年级，审题更是解题的灵魂，审题正确，则有可能所向披靡；审题失误，则有可能满盘皆输。即便是到了高年级，教师在教学中仍然要重视培养学生良好的审题习惯，有效提高学生的学习效率。

1. 做记号。教师要引导学生按要求审题，逐字逐句推敲，把题中简化了的成分清楚明白地标记出来，或把隐藏的条件补充完整，使题意更具体、明确。教师可以引导学生圈一圈、点一点，把已知的、未知的、疑惑的地方标注出来，以读代审，边读边画题中的重点字句，避免因审题不细、题意没弄清而造成列式错误。对于易混淆的关键词，在题中加着重号。

例如，在教学“一个数的亿位、千万位、千位上的数字都是9，其余各位上的数字都是0，这个数写作（ ），改写成用‘万作单位的数是（ ），省略亿后面的尾数是（ ）亿。”时，我引导学生在“改写”和“省略”的下方加上着重号，以便引起重视。

2.画图。在解决比较复杂的问题时，数量关系难以厘清，教师可引导学生通过画示意图或线段图的方法使题中的数量关系更直观，从而找到解决问题的突破口。

例如，教学“解决问题的策略”时，有这样一道题：“小明从家出发，先向东走了50米，再向北走了20米，接着向西走了40米，最后向南走了20米，你知道小明现在离家有多少米吗？”信息太多，学生一时间很难回答，于是我提示学生尝试画图表示题意。学生画完示意图后，题目中的数量关系就清晰地显现出来了，学生由此很快就解决了这道题。endprint

又如，教学“解决问题的策略”中的另一道题：“小宁和小春共有72枚邮票，小春比小宁多12枚邮票。两人各有多少枚？”

师：怎样整理条件和问题，使题意更直观、更清楚？

生（齐）：画线段图。

师：怎样画呢？请大家在草稿纸上画一画。

（学生动手画线段图，并展示自己的线段图，说明线段图表示的意义）

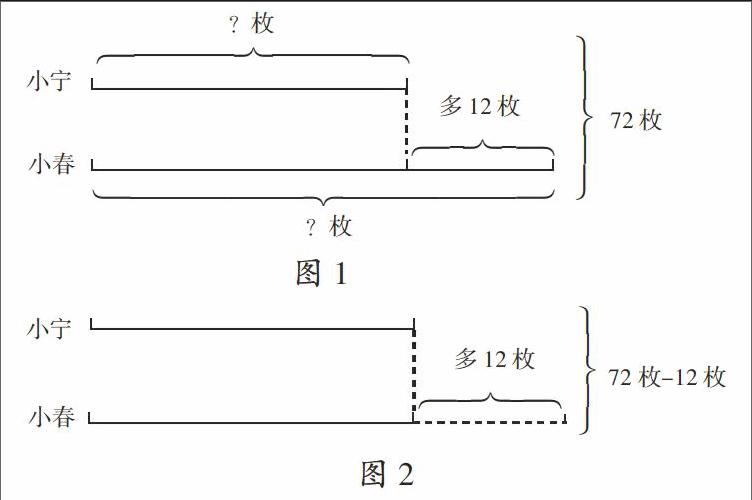
师（学生画出了线段图，如图1）：画图要完整，不仅要表示条件，还要标出问题。请把你的线段图完善一下。

师：只看线段图，你能说一说条件和问题吗？（隐去题目，学生发挥）你打算如何解决这两个问题呢？请大家尝试用不同的方法解决问题。请大家互相交流、讨论，说说自己的想法。

（学生借助线段图，交流不同的解题方法）

方法一（如图2）：

生1：减去小春比小宁多的12枚，两人现在的邮票数就同样多，用邮票总数72枚减去12枚就等于小宁邮票数的2倍，由此可以先求出小宁的邮票数。邮票总数-12=小宁的邮票数×2，求出了小宁的邮票数，那么小春的邮票数=小宁的邮票数+12。

方法二（如图3）：

生2：因为小春的邮票数比小宁的多12枚，所以，如果小宁的邮票数增加12枚，那么两人的邮票数就同样多，用邮票总数72枚加上12枚就等于小春邮票数的2倍，即邮票总数+12=小春的邮票数×2，求出小春的邮票数，则小宁的邮票数=小春的邮票数-12。

方法三（如图4）：

生3：邮票总数不变，把小春比小宁多出的12枚分一半给小宁，使两人的同样多，再分别求出小宁和小春的邮票数。

师：从线段图中，我们能看出什么？

生4：从线段图中，我们不仅能看出题目的条件和问题，还能清楚地看到题目中的数量关系。

师：好，现在请你选择自己喜欢的方法，列式并解答。

师：在刚才的解题过程中，是什么帮助我们快速理解题意并顺利答题的？

生（齐）：线段图。

这样的教学设计使学生在画线段图的过程中理解题意。教师给学生留有足够的时间去观察线段图，寻找数量之间的关系，激发学生主动探索解决问题的不同方法，学生在积累数学活动经验的同时获得了成功的体验，感受到画图的优越性。在这样的教学过程中，教师不但培养了学生利用几何直观分析、判断、推理的能力，还培养了学生的审题能力。

审题能力的培养并不是一蹴而就的，它是一个积累、反思、巩固的长期过程。学生审題能力的强弱，直接影响到解题能力的强弱。教师要明确“授人以鱼，不如授之以渔”，从低年级开始，重视培养学生的审题能力，帮助学生逐渐养成良好的审题习惯，形成较强的审题能力，从而提高学生的解题能力。

（责编 韦 迪）endprint