探究楔形玻璃板间液面曲线的方程

张舜尧

(焦作市第一中学 河南 焦作 454003)

1 引子

如图1所示，取两片尺寸相同的平板长方形玻璃板，一侧并齐，另一侧夹一根细金属丝，然后用夹子固定两片玻璃，使板间产生一个上下通透的狭窄的楔形空间．

图1 毛细现象实验装置图

将装置底部插入被染色的水中，液面在玻璃板间的楔形狭缝中逐渐上升，上升的高度随着玻璃板间缝隙厚度的减小而逐渐增大，液体颜色也随着玻璃板间缝隙厚度的减小由浓变淡，有色液面在玻璃板间形成一条平滑的曲线，生动地揭示了毛细现象的基本规律，实验画面呈现出物理学科的美感．

2 探究楔形玻璃板间液面曲线的方程

很多人对楔形玻璃板间液面曲线的性质产生了浓厚的兴趣，有的认为是抛物线，也有的认为是双曲线，大家各执一词，互不相让．

那么，楔形玻璃板间的液面曲线到底是什么性质的函数曲线呢？

2.1 探究影响平行玻璃板间液面高度的因素

如图2所示，设长为L的两个玻璃板A，B平行正对，板间相距为d，竖直插入水中．由于水能浸润玻璃，则玻璃板板间水膜的水位高出水面，产生毛细现象．

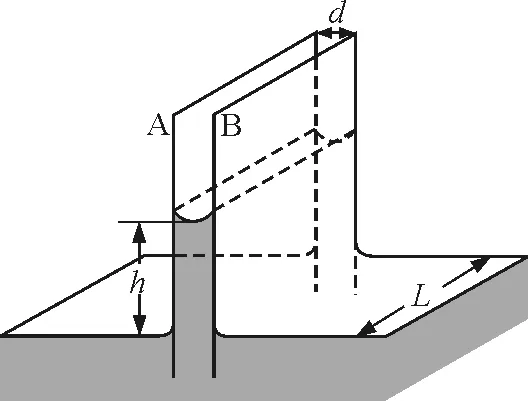
图2 玻璃板间毛细现象示意图

如图3所示，以玻璃板间高出水面的这部分水膜为研究对象，水膜两侧受到A，B玻璃板施加的水平压力NA和NB；水膜上方受到A，B玻璃板对液体凹型表面的斜向上的拉力FA和FB，拉力FA和FB与竖直方向的夹角均为浸润角θ，因为水浸润玻璃，所以浸润角θ为锐角；除此之外，水膜还受到自身重力作用．

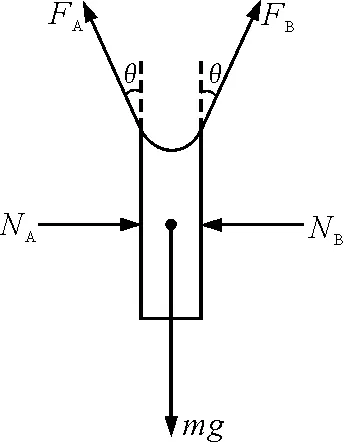
图3 玻璃板间液面受力分析图

设水的表面张力系数为σ，水的密度为ρ，当地重力加速度为g，则水膜的重力为

mg=hLdρg

(1)

由表面张力公式可知，玻璃板对水膜斜向上的拉力为

F=σL

(2)

当玻璃板间的水膜稳定后，由物体平衡条件可知

mg=2Fcosθ

(3)

由式(1)～(3)可得，水膜高出水平面的高度为[1，2]

(4)

由式(4)可知，平行玻璃板间的水膜高度h与玻璃板间的距离d成反比例关系．

2.2 探究楔形玻璃板间液面曲线的方程

如图4所示，以楔形玻璃板与水平面的交界线为x轴，以两玻璃板交界线为y轴，建立直角坐标系．

设玻璃板的宽度为a，金属丝的直径为D，则在距楔形尖端为x的位置，板间厚度为d为

(5)

考虑到两玻璃板间的夹角非常小，可以将水平向右方向上厚度均匀变化的楔形水膜视为一系列在水平向右方向上厚度成阶梯状递增的长条形等厚水膜，则每一个长条形等厚水膜的高度和厚度关系都将符合式(4)．

由式(4)、(5)可得，楔形玻璃板间的液面曲线的方程为

(6)

由式(6)可知，楔形玻璃板间的液面曲线为反比例函数曲线．

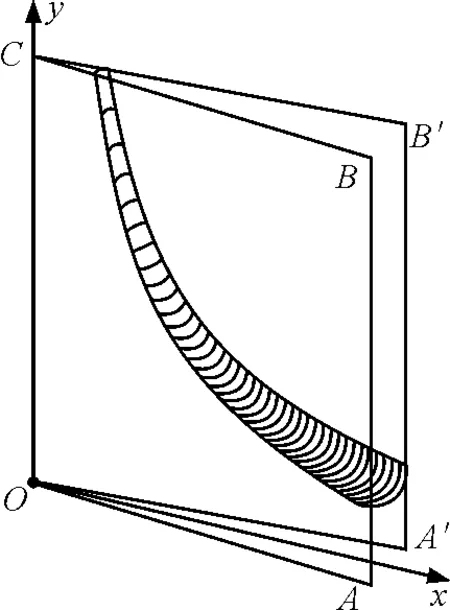
图4 楔形玻璃板间的液面曲线

3 实验验证

为了检验上述分析的可靠性，笔者在Photoshop中将实验照片中的玻璃板调节长方形，消除因拍摄方向与玻璃板不垂直带来的图像畸变，并将照片的长度设置为16 cm，高度设置为12 cm，使照片的尺寸与实物一致．

然后，将矫正过的玻璃板实验照片复制到几何画板中，并在几何画板中以楔形玻璃板与水平面的交界线为x轴，以两玻璃板的交界线为y轴，建立直角坐标系，绘制一条反比例函数曲线，缓慢调节反比例函数的比例系数，将反比例函数曲线与楔形玻璃板间的液面曲线相比对，对比结果如图5所示．

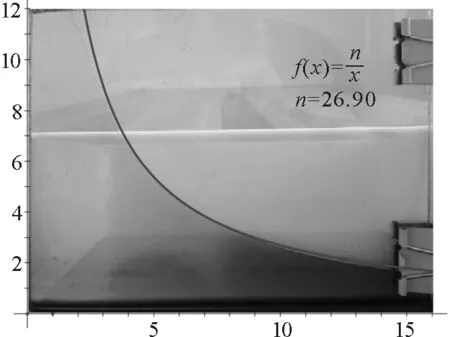
图5 液面曲线与反比例函数曲线比照图

显然，楔形玻璃板间的液面曲线与反比例函数曲线有着良好的重合度．

在本实验中，玻璃板的宽度a=0.16 m，金属丝的直径D=0.000 7 m，表面张力系数σ=0.072 N/m，水在玻璃板上的接触角θ=35°，水的密度ρ=

1 000 kg/m3，重力加速度g=9.8 m/s2．将上述数据代入式(6)可得，比例系数的理论值为n=2.75×10-3m2．

几何画板中坐标系的默认单位长度为1 cm，在此坐标系下的比例系数测量值为n′=26.90 cm2．

比较比例系数的实验值和理论值可得，比例系数测量值为理论值的0.978倍．在误差允许的范围内，比例系数的理论值与测量值相互吻合．

4 结论

两块长方形玻璃板一侧并齐，另一侧夹一细金属丝，可以组成楔形结构，用于毛细现象的实验演示．毛细现象发生时，液面提升的高度与缝隙的宽度成反比，楔形玻璃板间的液面曲线是反比例函数曲线．

1 何济洲.毛细管中液柱的高度.南昌大学学报,1995,17(2):80～82

2 程阳. 由于毛细现象液面上升高度计算的思考.数理医学杂志,2010,23(4):477～478