四辊冷轧机水平非线性主共振分析

尹鹏举， 李冲

（河南理工大学机械与动力工程学院，河南焦作 454000）

0 引言

随各行各业对冷轧板带材的需求量逐年增多，对其质量的要求也越来越高；然而，轧制过程中的振动却是影响其质量的重要因素之一，严重时甚至引起设备损坏，造成巨大的经济损失[1-2]。因此，国内外很多学者都在致力于轧机振动的研究，以求揭示其机理，便于控制。

轧机振动从振动形式上分为垂振、扭振和水平振动，国内外学者对垂振和扭振研究的比较多[3-10]，对水平振动研究的相对较少；然而轧机水平振动严重时会引起发生断带、堆钢和抱辊等事故。文献［11］考虑轧制界面动态的摩擦特性，分析了轧辊的水平振动模态。文献［12］考虑轧制界面间的变摩擦力特性，建立了板带轧机垂直-水平耦合非线性动力学模型。文献［13］建立了水平振动、垂振和扭振三种振动形式下的耦合模型，并研究了三者之间的相互耦合关系。但这些研究都是把水平振动作为激励，再和其他方向的振动进行耦合，而不能清晰地揭示其他方向的振动对轧机水平振动产生的影响。

针对上述问题，本文以垂直振动作为激励，水平振动为响应，通过对四辊冷轧机机构的合理简化，建立了一种新的轧机水平非线性动力学模型，来揭示四辊冷轧机的垂直振动对水平振动的影响。

1 四辊冷轧机机构动力学模型

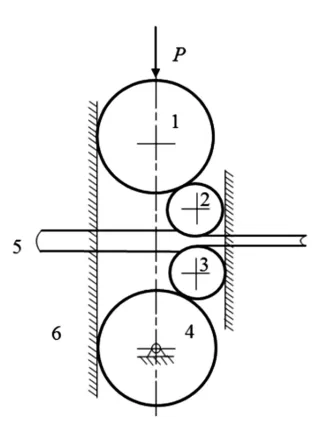
图1 四辊冷轧机机构工作简图

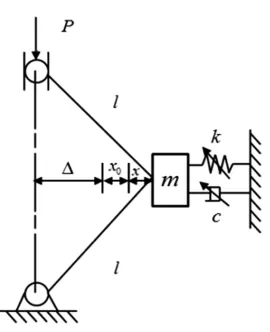
图2 动力学模型图

由于工作辊轴承座与机架之间存在间隙及工作辊与支承辊之间存在偏心，所以四辊冷轧机的机构模型如图1所示。

对模型做出以下假设：1）视轧辊为刚体；2）视上下支承辊在机构上对心；3）把上下工作辊视为一个整体且对心。则图1可简化为如图2的动力学模型。图2中：m为上下工作辊质量之和；k、c为水平方向的刚度、阻尼；Δ为偏心距；x0、x为平衡位置、偏离平衡位置的距离；l为工作辊和支承辊半径之和。

动态轧制力取为如下形式：

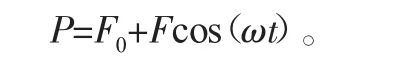
式中：F0为轧制力均值；F为轧制力浮动幅值；ω为轧制力变化频率。

考虑轧制界面摩擦力动态特性[14]及带钢波动等非线性因素，水平弹性恢复力和阻尼力写作如下形式：

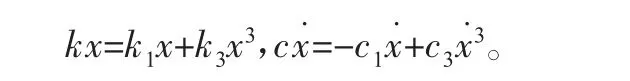
式中：k1、k3为线性刚度、非线性刚度；c1、c3为线性阻尼、非线性阻尼。

对m受力分析可得：

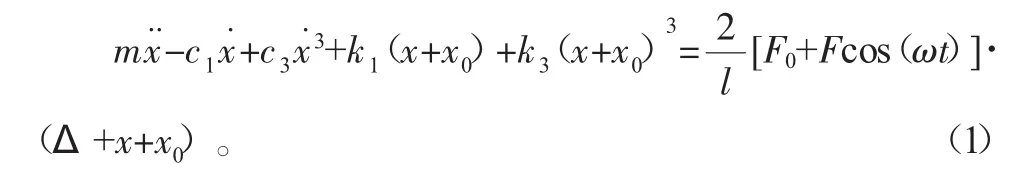
由平衡位置可得：

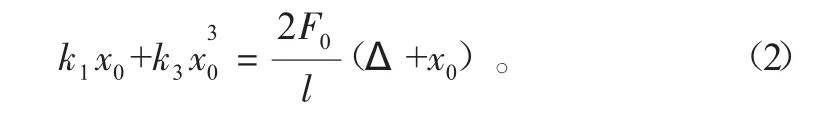
联立式（1）和式（2）可得：

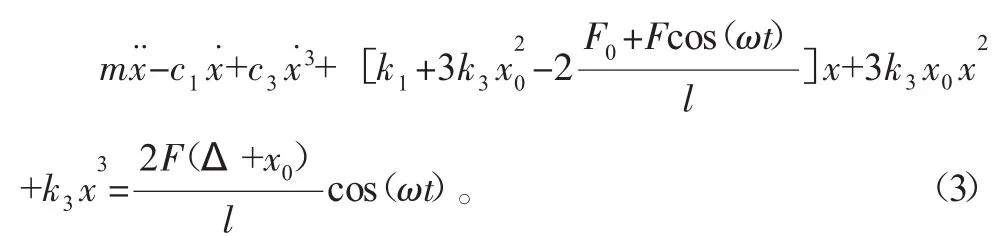
忽略较小的参数激励项并令：

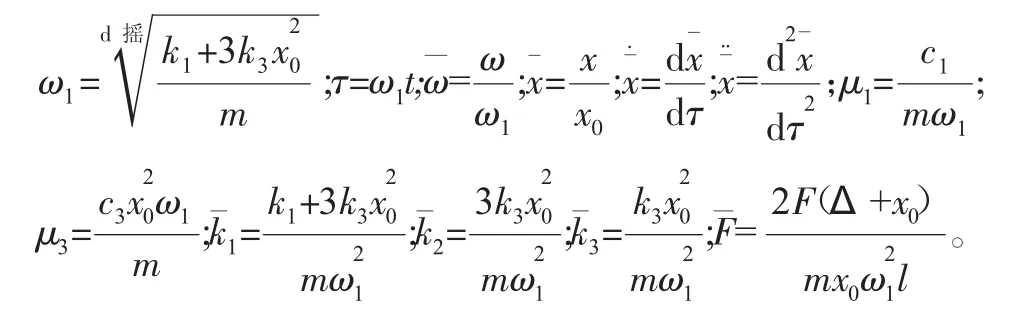
则式（3）可化为

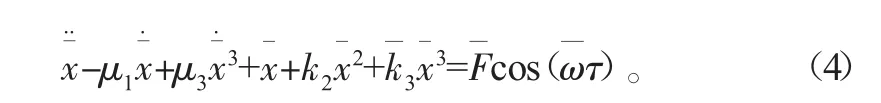
由此可知水平方向的振动为非线性的强迫振动。

2 主共振分析

采用多尺度法[15]对式（4）进行分析，设ε为小参数，令

并且认为线性阻尼项、非线性阻尼项、非线性刚度项和外激励项与ε2同量级，平方非线性刚度项与ε同量级，则

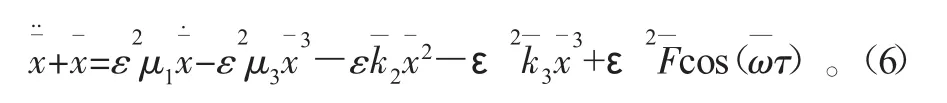
引入时间尺度Tn=εnτ，其中n=0,1,2…，则式（6）的二次近似解为

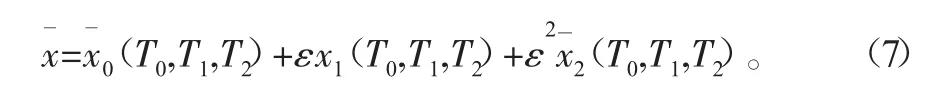
由于

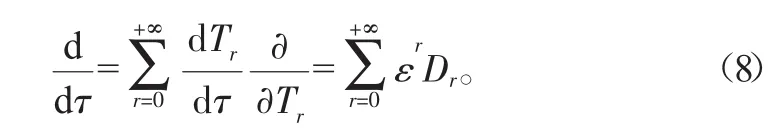
将式（5）、式（7）和式（8）代入式（6），比较ε的幂次，可以得到一组偏微分方程组:

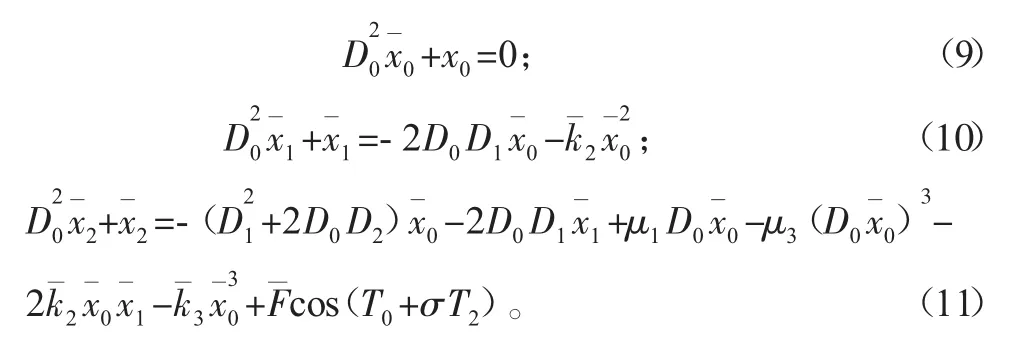
式（9）的解为

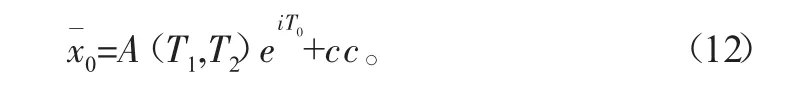
其中,cc代表其前面各项的共轭，下面不再说明。

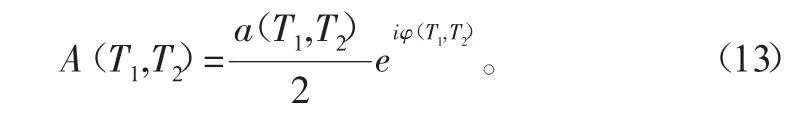
将式（12）代入式（10）中，可得

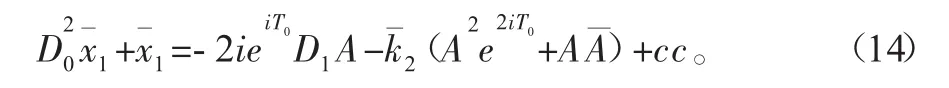
从式（14）中消除产生永年项的一次谐波项，可得D1A=0,则式（14）的解为

将式（12）和式（15）代入式（11）中，可得

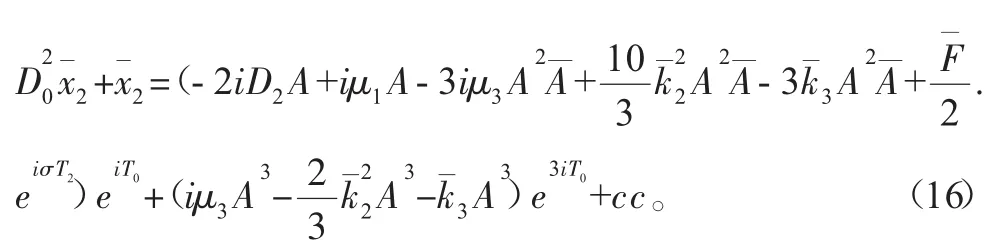
消除永年项可得

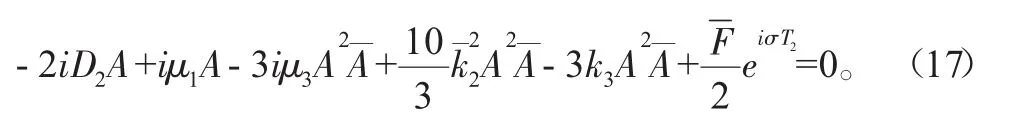
将式（13）代入式（17）中，并分离实部和虚部可得：

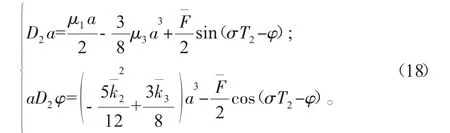
令σT2－φ=ψ,则式（18）变为

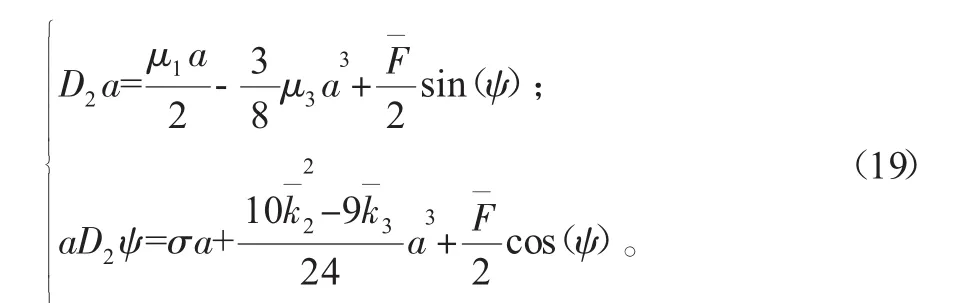
则二次近似解为

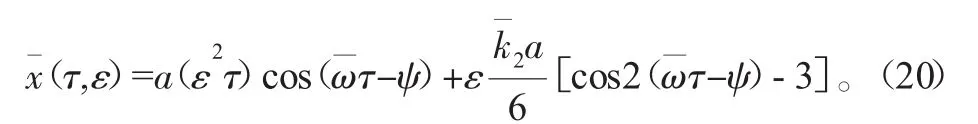
令D2a=D2ψ=0，可得

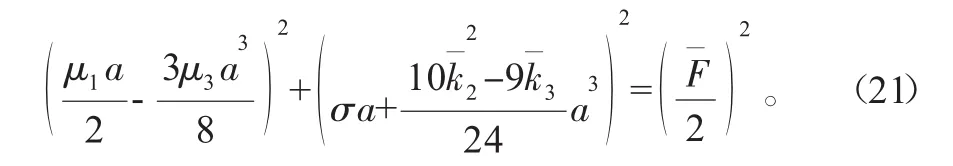
式（21）为幅频响应方程。

3 数值仿真

对式（21）进行仿真，如无特殊说明仿真参数取如下数据：质量m=18.4 t，长度l=1.0875 m，偏心距Δ=6 mm，线性阻尼c1=6×105N·s/m，非线性阻尼c3=2×1010N·s3/m3，线性刚度k1=1.2×1010N/m，非线性刚度k3=1.1×1020N/m3，轧制力均值F0=30 000 kN，浮动幅值F=3000 kN。

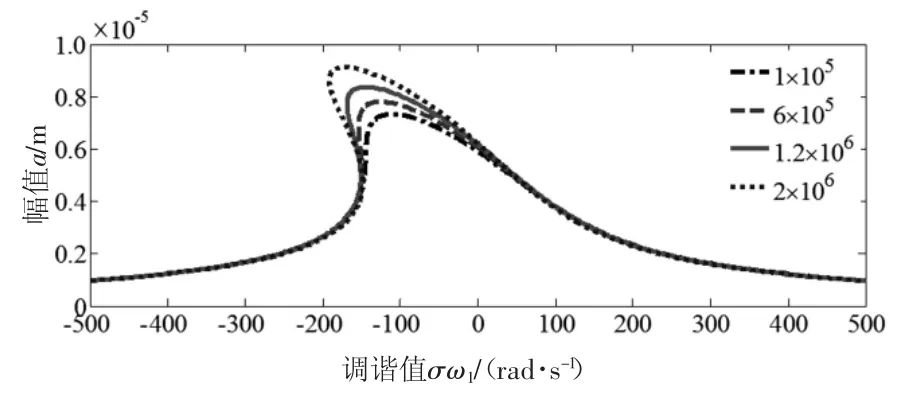
图3 c1对幅频特性的影响

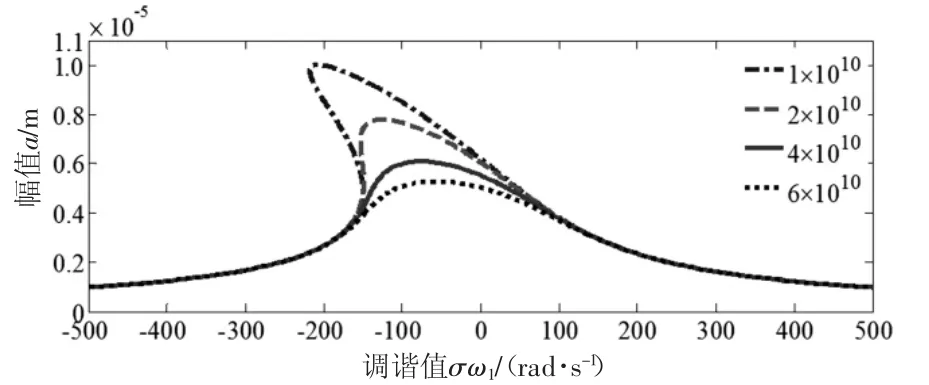
图4 c3对幅频特性的影响

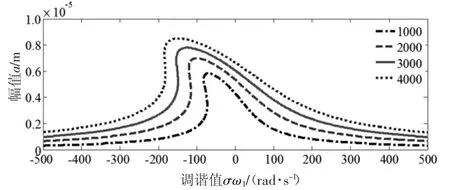
图5 F对幅频特性的影

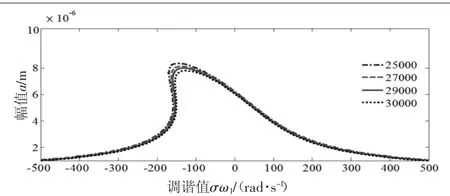
图6 F0对幅频特性的影响

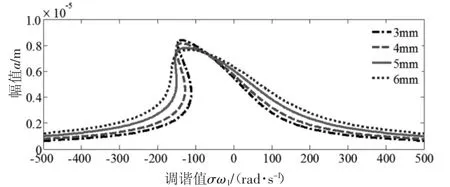
图7 Δ对幅频特性的影响

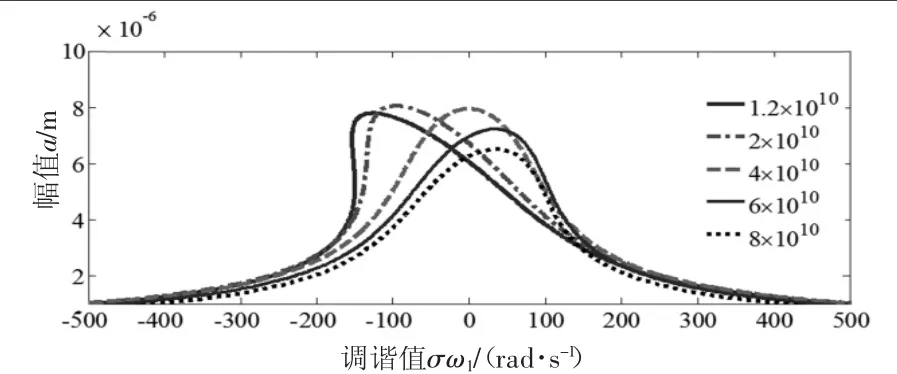
图8 k1对幅频特性的影响

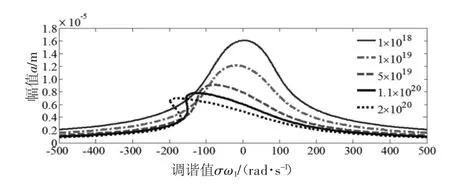
图9 k3对幅频特性的影响

由图3和图4可知，阻尼对主共振振幅具有很大的影响，随着线性阻尼c1的增大，振幅变大；非线性阻尼c3的增大，振幅变小；工程中可以通过控制轧制界面的摩擦因数及带钢的波动来控制阻尼的变化。

从图5和图6可以看出，随着F的增大，振幅幅值变大；F0的增大，振幅变小，但影响不大；因此可以通过控制垂直方向的振动，来控制水平振动的大小。

图7为偏心距Δ的影响。偏心距越小，共振区越弯、越窄、越高；偏心距越大时，相反；因此可以通过减小间隙减小共振区域，并且远离共振区。

图8和图9为刚度的影响。随着k1的增大，系统由软刚度向硬刚度变化，幅值先略为变大后变小；随着k3的增大，系统由硬刚度向软刚度变化，幅值一直变小；因此可以通过合理增加水平刚度，减小共振幅值，减弱系统的非线性。

4 结论

本文通过对四辊冷轧机机构的简化，建立了新的四辊冷轧机水平非线性动力学模型，通过仿真分析不同参数对轧机工作辊水平主共振特性的影响，可以得到如下结论：1）轧机工作辊水平方向的阻尼和刚度对其水平振动影响较大，应严格控制其波动。2）轧制力的波动幅值对轧机工作辊水平方向的主共振幅值影响较大，可以通过控制垂振来减小工作辊的水平振动。3）轧辊偏心距越小，共振区越小，共振幅值越大；偏心距越大则相反；可以通过合理调整偏心距，来减小四辊冷轧机工作辊的水平振动。

本文的研究补充轧机振动理论，并对实际的轧机振动控制具有一定的指导意义。

[1] YUKIO K,YASUHIRO S,NOBUO N,et al.Analysis of chatter in tandem cold rolling mills[J].ISIJ International,2003,43(1):77-84.

[2] 石野和成,小桧山昭彦,壁矢和久,等.压延机チャタリングの振动解析と对策[C]//日本机械学会论文集C编.2004:3009-3016.

[3] 陈勇辉,史铁林,杨叔子.四辊冷轧机非线性参激振动的研究[J].机械工程学报,2003,39(4):56-60.

[4] 林鹤,邹家祥,岳海龙.四辊冷轧机第三倍频程颤振[J].钢铁,1999,34(12):56-59.

[5] TLUSTY J,CHANDRA G,CRITCHLEY S,et al.Chatter in Cold Rolling[J].CIRP Annals-Manufacturing Technology,1982,31(1):195-199.

[6] NIZIOL J,SWI？TONIOWSKI A.Numerical analysis of the vertical vibrations of rolling mills and their negative effect on the sheet quality[J].Journal of Materials Processing Technology,2005,162(20):546-550.

[7] KIMURA Y,SODANI Y,NISHIURA N,et al.Analysis of Chatter in Tandem Cold Rolling Mills[J].Isij International,2007,43(1):77-84.

[8] 时培明,夏克伟,刘彬,等.含间隙多自由度轧机传动系统非线性扭振动力特性[J].机械工程学报,2012,48(17):57-64.

[9] 时培明,夏克伟,刘彬,等.多自由度轧机传动系统非线性非主振扭振特性[J].振动与冲击,2015,34(12):35-41.

[10] 高崇一,杜国君,张忠健.考虑多间隙影响的轧机主传动系统扭转分析[J].机械工程学报,2014,50(3):130-136.

[11]DWIVEDY S K，DHUTEKAR S S，EBERHARD P．Numerical Investigation of Chatter in Cold Rolling Mills[M]//Materials with Complex Behaviour II.Advanced Structured Materials,vol 16.Berlin:Springer,2012:213-227．

[12] 侯东晓,彭荣荣,刘浩然.变摩擦力下板带轧机辊系垂直-水平耦合振动特性[J].东北大学学报(自然科学版),2013,34(11):1615-1619.

[13] 王瑞鹏,彭艳,张阳,等.轧机耦合振动机理研究[J].机械工程学报,2013,49(12):66-71.

[14]李鸿光,闻邦椿.具有间隙和振动边界的自激振动系统的非线性振动[J].振动工程学报,2000,13(1):122-127.

[15] 胡海岩.应用非线性动力学[M].北京:航空工业出版社,2000:57-60.