球-平板微动摩擦行为研究
张明松, 王瑶, 程炼兵, 李宜, 伍强
(三峡大学机械与动力学院,湖北宜昌 443002)
0 引言
锯片在剧烈振动时,集中了大部分振动能量,噪声也加大,因此研究如何降低圆锯片横向振动问题具有重要的现实意义。大量实验研究显式采用阻尼技术的圆锯片降噪幅度可达20 dB(A)[1]。制备一种新型的阻尼接头结构,在圆锯片基体的一面熔覆一层阻尼接头结构,使其与另外一张基体复合在一起,并沿圆周焊接。阻尼接头和圆锯片基体的接触,可以看做是一个弹性半球体与一个刚性面板的接触问题;弹性球体与刚性面板的相互作用是复杂的高度非线性问题,在求解问题前,并不能知道具体的接触范围;且大多数接触问题都要涉及摩擦阻尼因素。
摩擦是一种复杂的接触过程,摩擦副发生整体滑动之前,接触面上部分区域将发生细微滑动[2-4],摩擦过程中接触区域、受力大小、受力方向以及接触面间的磨损和各种应力应变的不确定性,使人们至今还无法准确地对摩擦过程进行数学描述[5],这也使得研究摩擦的相关特性变得十分复杂。且摩擦的接触计算和接触面间的耗能机理研究一直是摩擦学理论分析的重点[6]。而接触问题具有高度非线性特性,目前在对接触类问题的处理过程中还存在两个困难[7]:1)在求解问题之前,并不知道接触区域;2)在动力学分析过程中,接触面之间是通过相互贴合面进行力和能量传递的,由于动力学接触过程力和能量传递的复杂性,并且经常是多部件的接触,会出现多种接触对的相互耦合与相互作用。大多数实际工程类装配体部件间的接触过程,并不是绝对平面,其表面粗糙度各不相同[8]。
传统的赫兹理论是在许多假设的前提下推导出来的近似解,利用赫兹理论只能解决一些规则几何形状的接触问题[9],不具备解决问题的普遍适用性。本文采用的ABAQUS[10]精于求解高度非线性问题而见长,能够解决所有工程类接触问题,且求解结果精度好。通过计算滑动过程接触耗能对系统势能总量的影响,可以描述宏观摩擦力在移动过程中所做的功,进而求得宏观的摩擦力大小和整体摩擦因数,对描述宏观接触动力学系统的耗能现象具有十分重要的意义。
1 半球头的法向阻尼因子计算
为了方便分析问题,将摩擦表面的接触滑动行为等效成为一个粗糙表面和一个刚性平面的接触,且等效粗糙表面具备各向同性的分形理论特征:且忽略接触过程中相邻接触微凸体之间的相互作用,以及弹塑性接触的强化作用[11]。在全体实数内,所有连续并处处可导且具备统计学自相似性的Weierstrass-Mandelbrot分形函数为
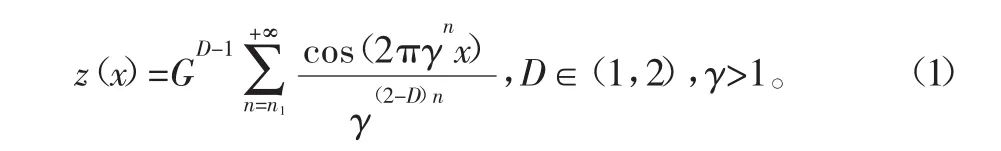
式中:x为轮廓沿接触平面上的位移;G为分形粗糙度;D为表面粗糙度轮廓分形维数;n为频率指数;n1为最低频率的初始项;γ为大于1的常数,它对应相应的波长。
由于粗糙表面轮廓对工程研究可认为是连续的,而且随着放大倍数的增加,在任何一点上都会呈现出更多的具有统计自相似自仿射性的粗糙度细节。根据以上分形理论定义[12],为了使本接触类型的表面构建具备自相似性,需重新构建傅里叶级数的振幅并改变函数沿轴向方向的变化趋势。修改后的分形函数为:
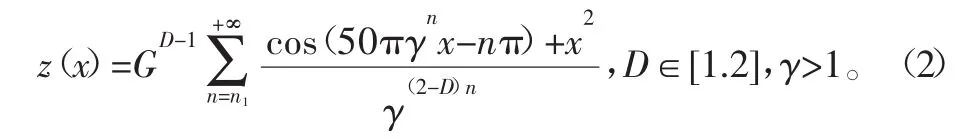
其整体形貌变化趋势如图1所示。以此来表示阻尼接头的几何形状。
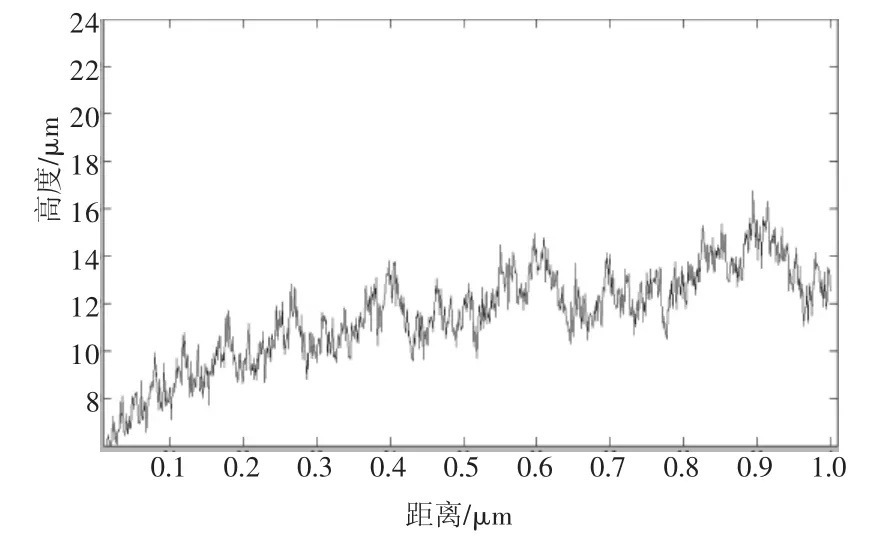
图1 阻尼接头表面粗糙度
对于一个给定点截面面积为a的微凸体,由式(2)得出峰元顶端的变形量δ,取得出单个微凸体的变形量为[13]
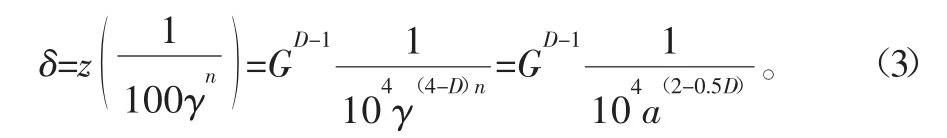
式中,a为峰元接触点面积,且满足:

微凸体与刚性表面接触示意图如图2所示,根据其几何关系:R2=(R-δ)2+r2,略去δ2高阶无穷小量得2Rrδ=r2;再结合面积公式a=πr2,得到凸体的曲率半径为

将式(3)带入式(5)可得:

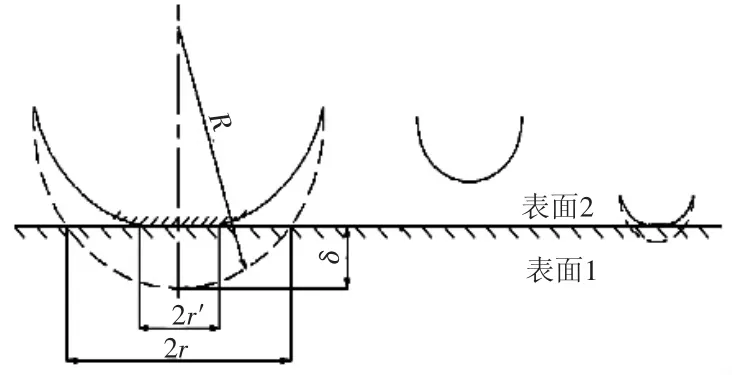
图2 当量粗糙度表面1与理想刚性表面2的接触
根据赫兹理论弹性接触点上接触面积与载荷的关系式,峰元承受的垂直于柔性结合部的法向弹性载荷[14]:
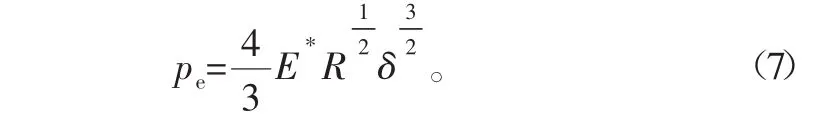
结合面的复合弹性模量可以表示为
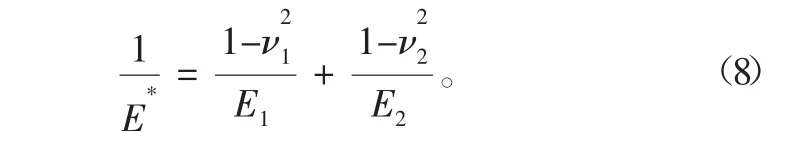
式中:E*为两接触复合材料的弹性模量;E1、E2为两接触材料的弹性模量;ν1、ν2为两材料的泊松比。
而本节中一接触部件为刚体,令E1为阻尼接头的弹性模量,即
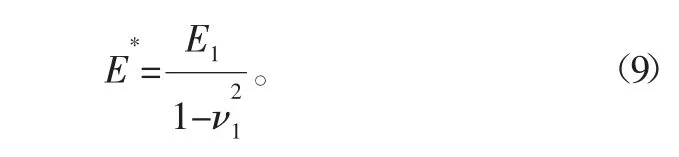
将式(3)、式(6)代入式(7)中整理得
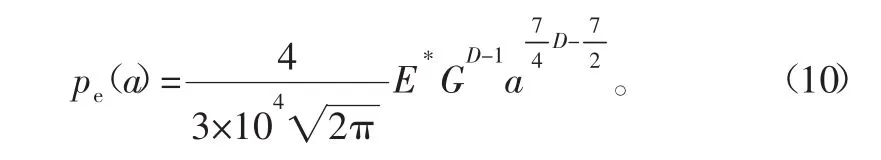
单个峰元在接触部分承受着法向弹性载荷和塑性载荷,塑性接触点上截面积α与塑性接触载荷pp的关系为[15]

其中H为较软材料的硬度。
对于峰元的描述,除半径外还应有高度参数,如峰高、峰距、两表面间距、峰与表面间的距离在实际接触面积的计算中,先接触峰元的接触面积随接触的继续发展由小变大,随后又有新的峰元进入接触。其接触点面积a的分布密度函数为:
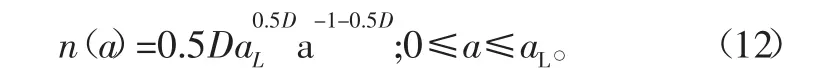
式中aL为峰元的最大变形接触面积。
弹性接触区域的弹性应变能为
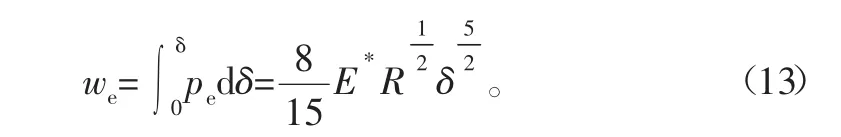
弹性区域产生的应变能为
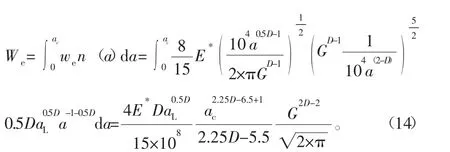
塑性接触区域单个微凸体塑性应变能为
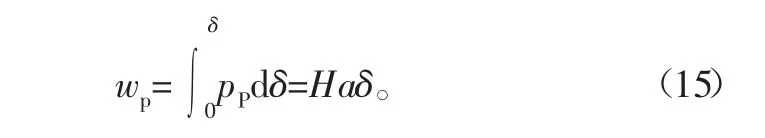
因而塑性接触区域总的应变能为
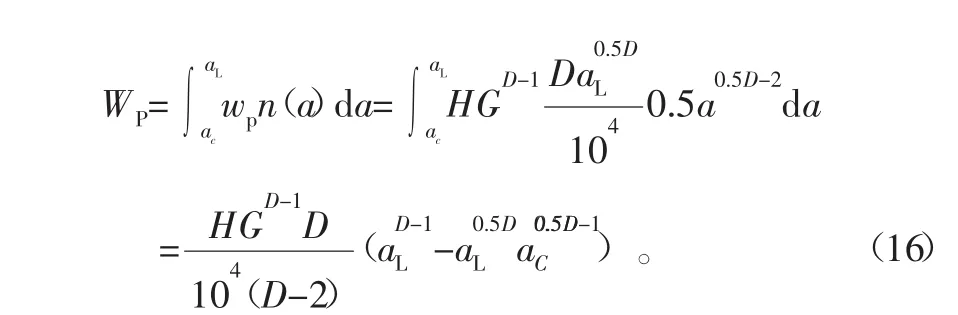
式中aC到aL为弹性区域面积转变为塑性区域面积。
通过阻尼产生的机理,即用损耗的振动能量和总的振动能量的比值来衡量结构的阻尼特性。在接触表面不考虑摩擦时,接触力为法向力。由定义可得出阻尼接头的损耗因子计算公式,把式(14)、式(16)代入可得
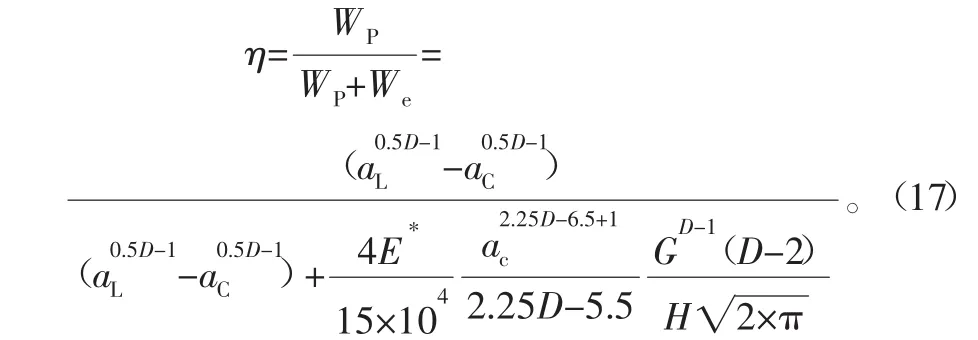
而在整张圆锯片上有k个这样的阻尼接头,因此,取所有接头的平均阻尼表达式为

本文取每个阻尼结合面法向损耗因子为0.03。
2 球-平板有限元接触分析
2.1 阻尼接头应力应变
半球头与平板间为接触摩擦,在ABAQUS有限元分析过程中,假设平板为刚性部件,半球头为变形部件,取法向力为10 N,对半球头施加沿着X方向的速度场,速度为100 mm/s,法向阻尼因子取0.03,接触截面间的摩擦因数取0.05,滑动距离为0.5 mm。控制相关约束条件,提交JOB运行,最后查看结果。
图3中,(a)、(b)、(c)分别显示了滑动半球头在X、Y、Z三个方向的应力云图,其中可以从应力数据上可以看出,沿着X方向上所受到的应力最大,这是因为半球头在运动方向上由于受到摩擦阻尼的作用使得半球头产生切向应力所致。整体总应力变形见图3(d),从应力云图颜色深度部分可以发现在接触区域所受到的接触应力最大。
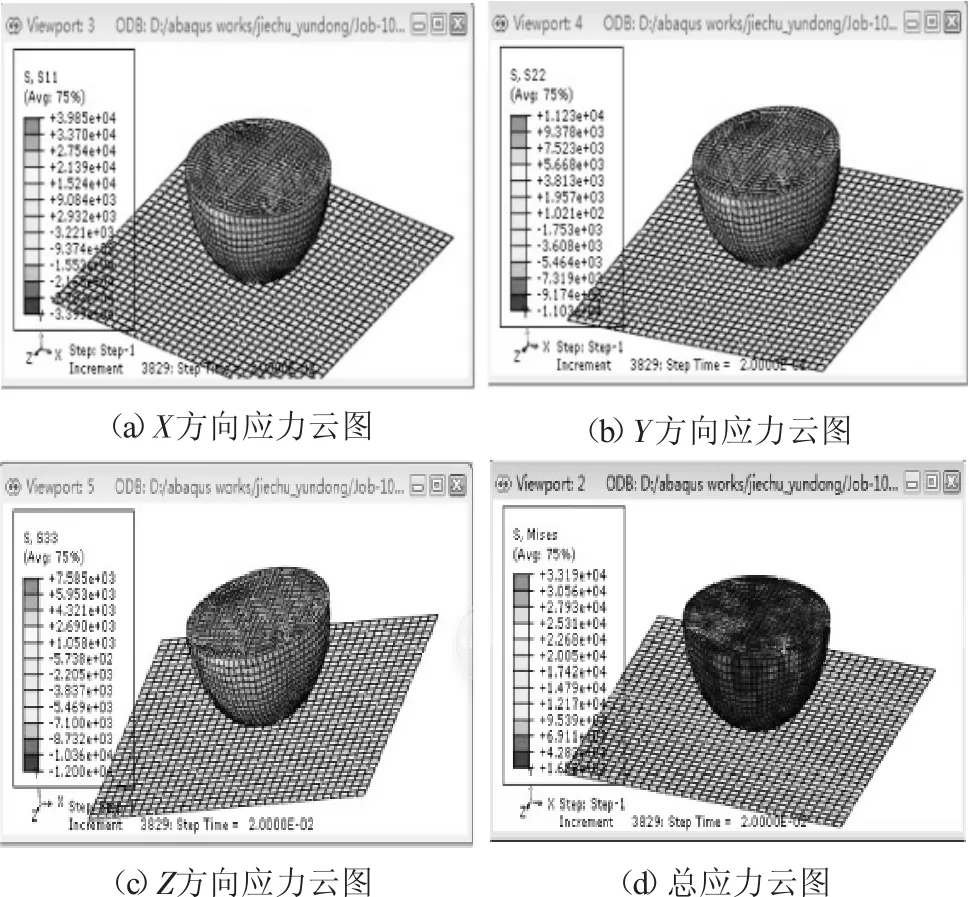
图3 接触运动应力云图
2.2 摩擦能分析
从能量的方面来看。本文提取6种能量曲线,半球头能量项作用的曲线图如图4所示,分别是摩擦耗能曲线(ALLFD),伪应变能曲线(ALLAE),内能曲线(ALLIE),动能曲线(ALLKE),非弹性应变能曲线(ALLPD)以及弹性应变能曲线(ALLSE)。可以看出,半球头在受到法向力F作用时系统的内能是不断增加,在半球头刚准备运动之前,速度v赋予给阻尼半球头,致使半球头的动能最大,而在发生运动以后,由于受到切向摩擦力的作用,动能缓慢减少,半球头受到力F的作用时,半球头与平板的接触面积会增大,此时摩擦阻尼也会增大,系统的内能将变大,而动能将进一步减少,半球头在法向方向上存在法向阻尼,使应变滞后于应力,从而使弹性应变能和塑性应变能发生更加缓慢的变化。
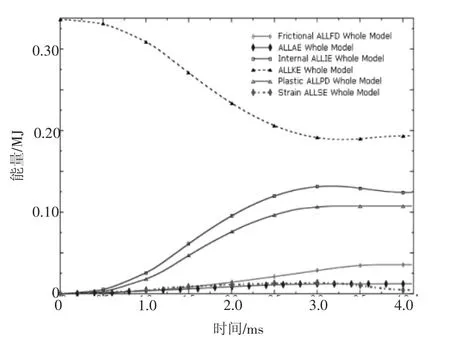
图4 阻尼接头能量项作用的曲线图
运用后处理命令将摩擦耗能曲线(ALLFD)和动能曲线(ALLKE)添加到combine函数中,使摩擦耗能曲线除以系统的动能曲线,得到如图5的能量损耗率图形,可以看出摩擦损耗的能量占系统总动能的18%左右。
求解系统的总耗能,耗能量包括系统的摩擦耗能、系统的塑性应变能,系统的总能量是动能和内能的总和,其表达式为
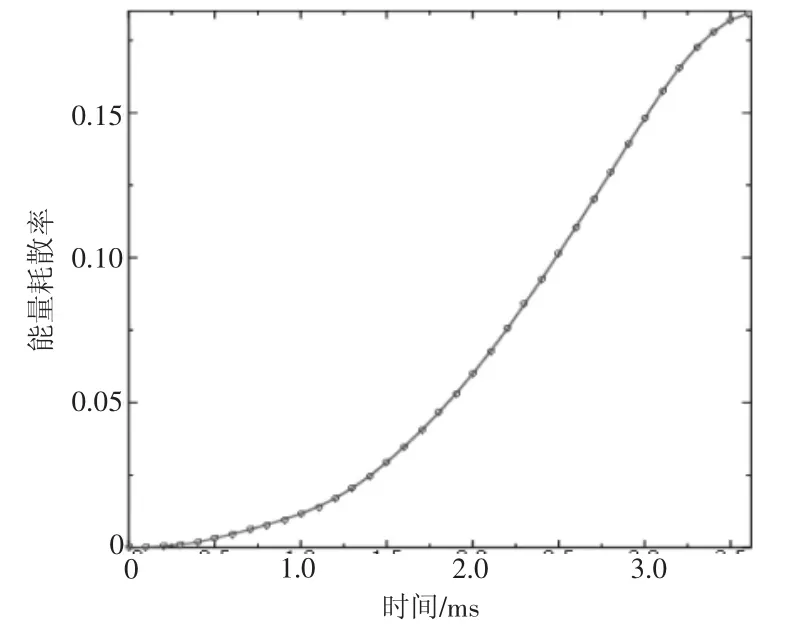
图5 摩擦能量损耗率
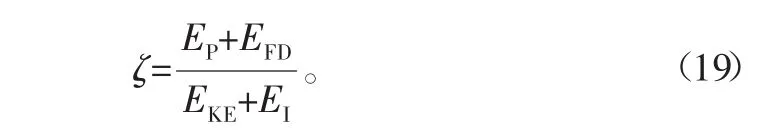
将非弹性应变能曲线(ALLPD)、摩擦耗能曲线(ALLFD)、动能曲线(ALLKE)和内能曲线(ALLIE)同样添加到combine函数中,使前两项耗能量除以后两项能量,得到如图6系统能量耗散率图,可以看出耗散的能量占系统总能量的44%左右。
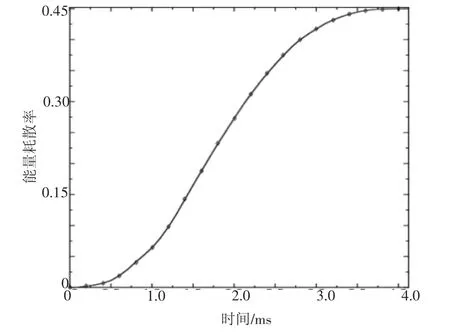
图6 系统能量耗散率图
3 结 论
将阻尼接头看成是一个半球形模型,锯片基体看作是缸体部件,与变形部件相比,缸体部件有很高的计算效率。通过对半球头与平板进行显式动力学分析,得到半球头能量项作用的曲线图,分析可知发生运动后,半球头的动能减少,内能增加,而增加的内能则是以热能的形式传递出去了,达到了耗能的目的。通过后处理得到的能量耗损率图和系统能量耗散率图,可以看出,摩擦耗能占该系统总动能的18%,而耗散的能量占系统总能量的44%左右。通过以上分析最终得出,阻尼接头在微小范围内的滑动能够有效地起到摩擦耗能的作用,因而阻尼技术可广泛应用于需要减振降噪的零件或设备。
[1] 孙庆鸿,张启军,姚慧珠.振动与噪声的阻尼控制[M].北京:机械工业出版社,1993:44-48.
[2] COURTNEY J S,EISNER E.The effect of a tangential force on the contact of metallic bodies[J].Proc.R.Soc.,1957,238:529-550.
[3] BHUSHAN B,ISRAELACHVILI J N,LANDMAN U.Nanotribology:Friction,wear and lubrication at the atomic scale[J].Nature,1995,374:607-616.
[4] BEN-DAVID O,RUBINSTEIN S M,FINEBERG J.Slip-stick and the evolution of frictional strength[J].Nature,2010,463:76-79.
[5] PEITGEN H O.Beno it B mandelbrot(1924-2010)[J].Science,2010,330(6006):926.
[6] 谢友柏.摩擦学的三个公理[J].摩擦学学报,2001,21(3):161-166.
[7] 博嘉科技.有限元分析软件-ANSYS融会贯通[M].北京:中国水利水电出版社,2002.
[8] NAYAK P R.Random process model of rough surfaces[J].Transactions of the ASME Journal of Lubrication Technology,1971,93:398-407.
[9] HERTZ H.On the contact of elastic solids[J].Reine Angew.Math,1881,(92):156-171.
[10] 石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2006.
[11]MAJUMDAR A,BHUSHAN B.Fractal Model of Elastic-Plastic Contact Between Rough Surfaces[J].Journal of Tribology,1991,113(1):1-11.
[12] 朱华,姬翠翠.分形理论及应用[M].北京:科学出版社,2011:10.
[13]尤晋闽,陈天宁.结合面法向动态参数的分形模型[J].西安交通大学学报,2009,43(9):91-94.
[14]波波夫.接触力学与摩擦学的原理及其应用[M].北京:清华大学出版社,2011:47.
[15]YAN W,KOMVOPOULOS K.Contact analysis of elasticplastic fractal surfaces[J].Journal of Applied Physics,1998,84(7):3617-3624.

