回采巷道底板破坏范围及其影响研究
黄庆享,郝高全
0 引言
我国煤炭开采深度以每年8~12 m的速度递增[1],埋深的增加导致高应力软岩巷道底鼓问题突出[2-5]。关于软岩巷道底板破坏机理和支护问题,国内学者开展了大量研究。杨建中从巷道底板岩体极限承载力入手,研究了巷道底鼓机理,认为底鼓主要是超过了极限承载力,发生剪切破坏和挤出造成的[6];董方庭等提出了巷道围岩的松动圈理论,指出围岩松动圈的范围越大,巷道支护越困难,给出了底板松动圈的破坏深度[7];姜耀东等根据底板岩性和应力水平的差异,将底鼓分为4种形式:挤压性底鼓、挠曲褶皱性底鼓、遇水膨胀性底鼓以及剪切错动性底鼓,将底板研究引向深入[8]。康红普等对深部软岩巷道稳定性进行了深入研究,认为底鼓是由底板岩体塑性流动、岩石扩容、水理作用和弯折断裂多种作用的结果[9];初明祥等研究了底板断裂、隆起和帮脚移动特征,认为底鼓始于巷道底角与底板中部,两帮脚发生外移是造成底鼓的主要原因[10];王卫军等研究认为巷道两帮和底板存在相互影响,提出加固两帮可在一定程度上控制回采巷道底鼓[11];刘泉声等提出底鼓主要是软弱破碎围岩的挤压流动变形造成的[12];张红军等提出采用“锚杆”和“锚注”联合支护能有效减小围岩变形量,提高承载结构的整体性与承载能力[13];袁亮等提出了基于“应力状态恢复改善、围岩增强、破裂固结与损伤修复、应力峰值转移与承载圈扩大”的深部岩巷围岩稳定控制理论[14];黄庆享等基于多年的实测和实践,认为巷道“底板-两帮-顶板”之间存在相互影响,指出巷道围岩控制应当将“底-帮-顶”作为一个整体进行控制,据此提出了巷道围岩“极限平衡圈”支护理论,以及“治顶先治帮,治帮先治底”和“整环控制”的软岩巷道支护原则[15-16]。上述研究为文中提供了良好基础,其中关于底板破坏深度的确定是底鼓控制的重要参数,对此目前的认识不统一,研究尚不深入。
文中以陕西省蒋家河煤矿煤层巷道为背景,通过现场实测、物理模拟和数值计算,揭示底板破坏的机理,通过理论分析确定巷道底板破坏深度,完善了“极限平衡圈”理论。
1 巷道变形破坏特征
陕西省彬县蒋家河煤矿主采煤层埋深为545~641 m,埋深大,地应力较高。煤层底板主要为砂质泥岩及炭质泥岩,强度低。ZF204运输顺槽设计宽5.0 m,高3.1 m,巷道顶板出现喷层开裂等变形,顶底板移近量达1 300 mm.巷道两下帮变形量比较严重,靠近采空区侧下帮变形量300~440 mm,工作面侧下帮变形量50~260 mm.
巷道总长1 270 m,底鼓量在400~900 mm的巷段长度超过450 m,巷道底鼓量超过900 mm的长度超过300 m,局部最大底鼓量达1 100 mm.巷道底鼓形状为中间大,两侧小,如图1所示。

图1 巷道变形特征(mm)Fig.1 Deformation characteristics of entry
2 底鼓型巷道变形破坏实验分析
2.1 巷道变形破坏物理模拟
根据地质报告,巷道围岩物理力学参数见表1.采用几何相似比1∶25,进行物理相似模拟实验。采用河砂做骨料,选取石膏、大白粉做胶结材料,采用云母粉模拟原生层理与构造裂隙,相似材料及配比见表2.模型尺寸为:1 200 mm×909 mm×120 mm,模型巷道宽20 cm,高12.4 cm,如图2所示。
根据实测采动支承压力峰值,实验加载至1.68倍原岩应力模拟采动影响,加载后巷道变形破坏有如下规律。

表1 煤岩层物理力学参数Tab.1 Physical and mechanical parameters of rock

表2 相似材料配比Tab.2 Similar material proportion

图2 巷道物理模拟模型(cm)Fig.2 Physical simulation model of entry
1)顶底板移近量1 350 mm,两帮移近量700 mm,顶板下沉量为350 mm,底鼓量1 000 mm.模拟巷道变形情况基本与实际相符;
2)巷道围岩变形破坏主要为底板破坏,底板破坏深度3 750 mm;
3)巷道顶板和两帮下沉,两帮脚内收,底板中部向上隆起,两帮脚底板向内平移,形成以底鼓为主的收敛移动,如图3所示;
4)巷道底板和帮脚处围岩变形最为剧烈,以挤压流动型变形破坏为主,如图4所示。

图3 实验巷道变形Fig.3 Deformation of entry
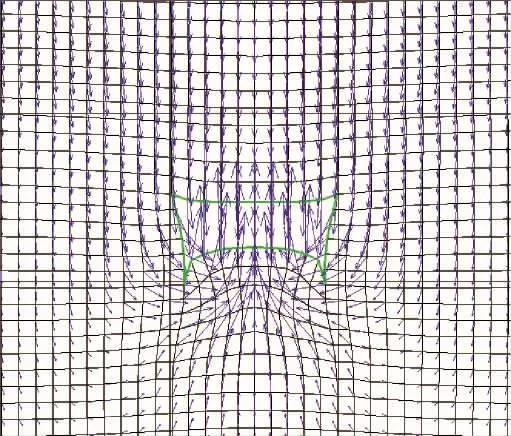
图4 巷道变形位移矢量Fig.4 Deformation displacement vector of entry
2.2 巷道底板破坏数值模拟
依据巷道围岩地质条件,采用FLAC3D模拟软件建立数值模拟模型。模型长宽高尺寸为25 m×25 m ×23 m.覆岩载荷为16.25 MPa,下边界z方向固定,左右边界x方向位移固定,前后边界y方向位移固定(图5)。
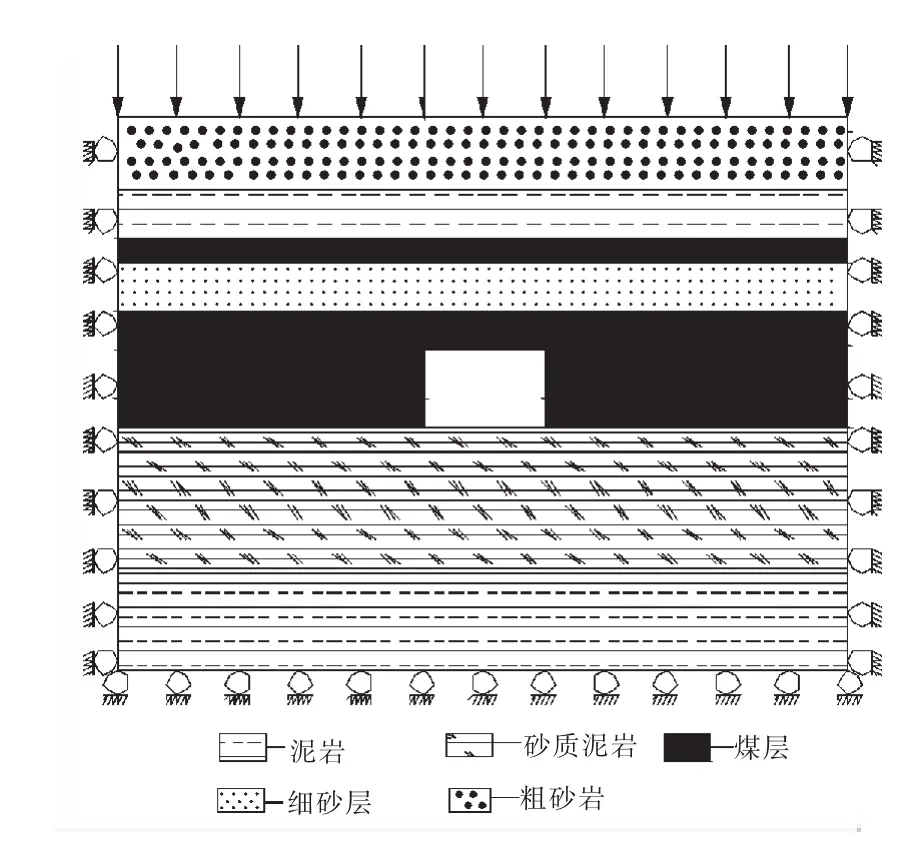
图5 模型边界约束Fig.5 Model boundary
巷道围岩位移规律:巷道垂直位移分布为巷道中部底鼓量最大达800 mm,两底脚处底板底鼓量较小为300 mm,顶板最大下沉量500 mm,两肩下沉量300 mm,顶板相对于两肩下沉200 mm,顶底板最大移近量1 300 mm,是原巷道高3.1 m的41.9%.巷道底鼓变形量中间大两边小(图6),水平位移分布为巷道上帮移近量200~300 mm,中帮最大移近量600 mm,底板两侧移近量500 mm,为巷宽的12%(图7)。

图6 巷道垂直位移分布Fig.6 Vertical displacement of entry
巷道围岩应力分布规律:巷道最大垂直应力30 MPa,位于两帮2~4 m深处(图8);最大水平应力14 MPa,位于巷道顶板2.5~4 m 和底板4.5~6 m处(图9),在巷道周围形成应力卸荷圈。
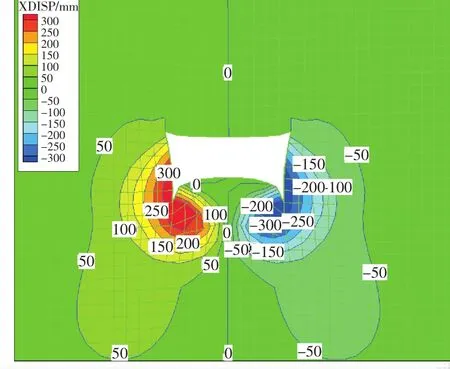
图7 巷道水平位移分布Fig.7 Horizontal displacement of entry
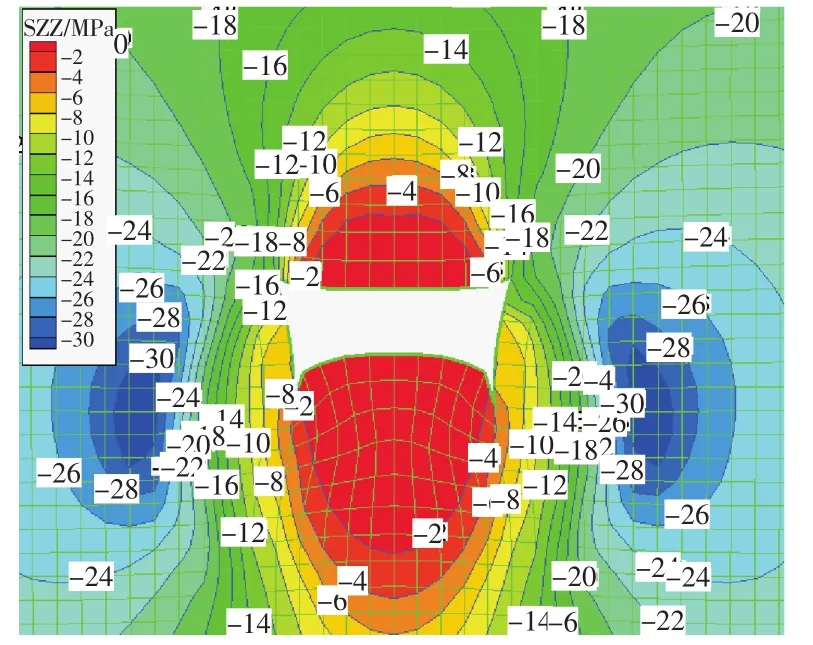
图8 巷道垂应力分布Fig.8 Vertical stress of entry
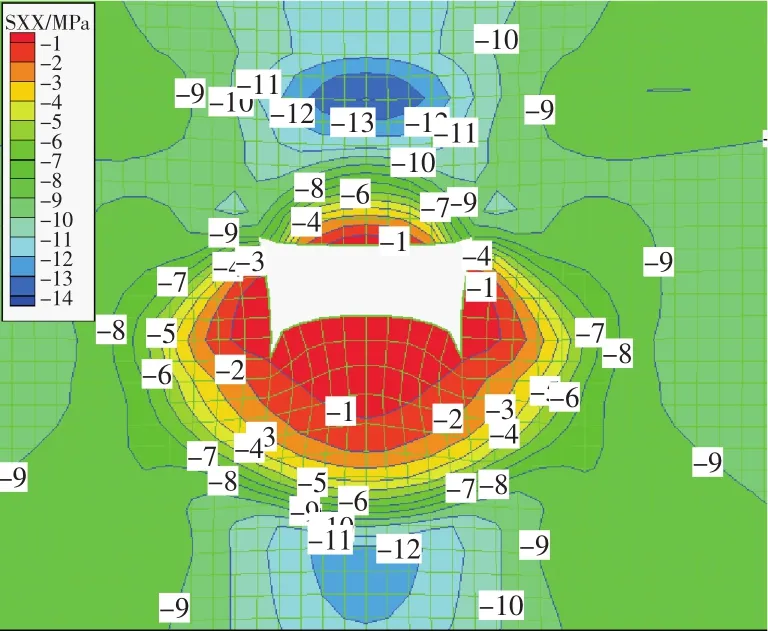
图9 巷道水平应力分布Fig.9 Horizontal stress of entry
3 巷道底板破坏深度分析
3.1 建立巷道底板破坏力学模型
对于挤压流动型底鼓巷道,由于底板强度弱,引入地基极限承载力理论进行分析。选取巷道一侧作为研究对象,建立巷道底板破坏力学模型如图10所示。

图10 底板破坏力学模型Fig.10 Mechanical model of floor failure
受煤帮均匀载荷P和底板上均布载荷q的作用,底板oac区与ocb区分别处于主动和被动塑性应力状态。底板最大破坏(极限平衡区)深度为hd.主动契体A上的最小主应力为σ3A,最大主应力为σ1A;被动契体B上的最小主应力为σ3B,最大主应力为 σ1B.根据极限平衡条件,σ3A=σ1B.A区底板最大主应力为垂直应力,B区最大主应力为水平应力。
3.2 底板极限承载力
3.2.1 不考虑底板自重的极限承载力
被动破坏区B的最小主应力为σ3B=q,主动破坏区A的最大主应力为岩体极限承载P,内摩擦角α=45°+/2,为岩石的内摩擦角;c为内聚力。被动破坏区B的最小主应力为σ3B与最大主应力σ1B.根据Mohr-Coulomb强度准则

将σ3B=q代入(1)式得

由极限平衡条件,σ3A=σ1B得

主动破坏区A的最小主应力为σ3A与最大主应力σ1A,根据Mohr-Coulomb强度准则,有

将(3)代入(4)得
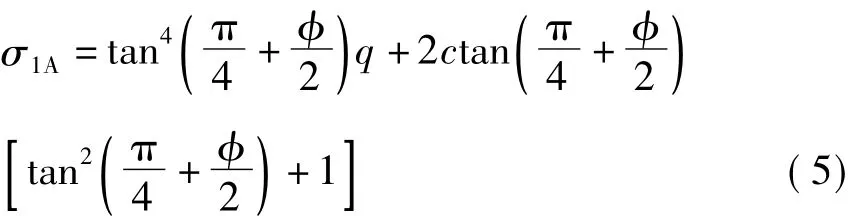
由σ1A=P可得巷道两帮底板极限承载力

若巷道底板无支护,即q=0时
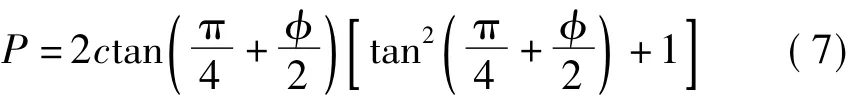
可见,底板极限承载力与内聚力成正比,与内摩擦角正相关。
郑颖人等认为,岩土体渐进失稳过程中强度参数是不断衰减的,并且内聚力和内摩擦角的衰减速度和程度不同[17]。借鉴双折减系数强度折减法[18]提出底板强度折减系数η,折减后内聚力c*为ηc,内摩擦角*为 arctan(ηtan),可得

内聚力 c为1.72 MPa, 为35°时,可求出极限承载力P随着η的减小而降速减小(图11)。

图11 底板极限承载力与折减系数的关系Fig.11 Ultimate floor bearing load vs.reduction factor
3.2.2 考虑底板自重的极限承载力
考虑底板自重时,设煤帮处底板破坏深度为hd,底板岩层容重为γ,则被动破坏区B的最小主应力为σ3B=q+1/2γhd,主动破坏区A的最大主应力为岩体极限承载P为
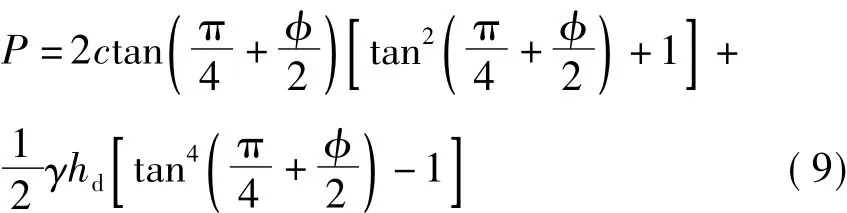
可见,不计自重的极限承载力略小,一般可按照不计自重的公式(8)进行计算。
取底板容重 γ=24 000 N/m3,内聚力c=1.72 MPa,底板破坏深度hd=3.57 m,分别取 =28°~38°,可得P随内聚力c的减小而线性减小,随内摩擦角的减小非线性减小(图12)。
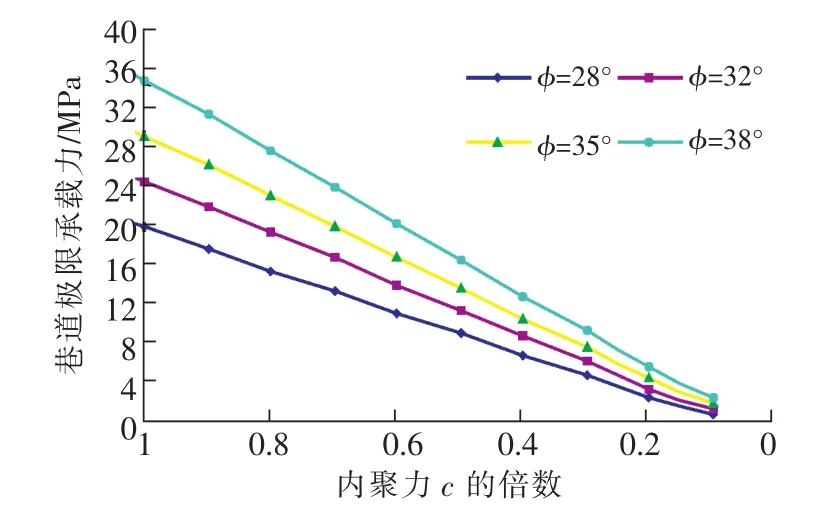
图12 巷道底板极限承载力P与c和的关系Fig.12 Ultimate floor bearing load P vs.c and
3.3 巷道底板稳定性分析
考虑巷道开挖后的侧向支承压力峰值系数k,巷帮承受的载荷为P1

式中 P0为巷道原岩应力,MPa.
则巷道底板稳定性判据为

3.4 巷道底板破坏范围确定
根据土力学普朗德尔-瑞斯纳、梅耶霍夫与汉森等计算地基极限承载力,可将极限平衡区的发展规律,简化为主动极限区、被动极限区与过渡区[19]。在《矿山压力与岩层控制》中,利用其计算采场底板破坏深度[20]。建立底板极限平衡底板破坏范围模型如图13所示,图中,L为巷帮下部底板极限平衡区宽度,m;γθ为oc边长,m;γθ为过渡区螺旋半径,m;hbd为巷帮底板破坏区深度,m;hdmax为底板最大破坏深度,m;lmax为底板破坏最深点位置与煤帮距离,m.
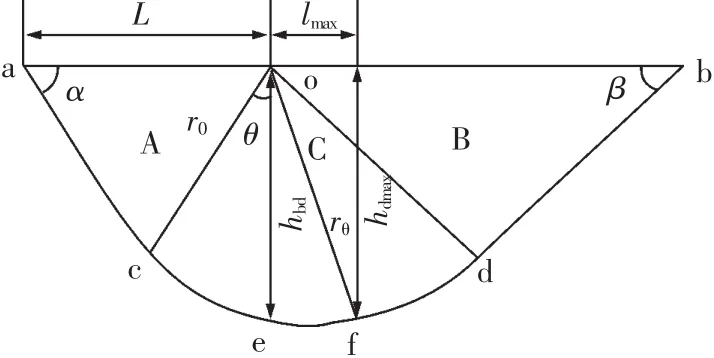
图13 巷道底板极限平衡深度计算模型Fig.13 Model of limit equilibrium depth of floor
图13 中A主动极限区和被动极限区B的滑移线均为两组直线。其中α=π/4+/2,β=π/4--2.而过渡区C的滑移线一组为对数螺线。通过文献[20]可知θ=π/4+/2时破坏深度最大为

当θ=π/4-/2时,帮脚底板破坏深度

将(14)代入(12)和(13)中得

由(18)可以求得

可以看出,值一定时,底板岩体帮脚破坏深度随煤帮极限平衡区宽度线性增长。
巷道底板破坏最大深处与巷帮距离为

4 底鼓巷道围岩极限平衡圈支护分析
4.1 巷道围岩极限平衡圈模型
“极限平衡圈理论”认为,巷道底板破坏会引起两帮破坏扩展,两帮破坏又会导致顶板破坏范围增大,应当将“底-帮-顶”作为一个相互影响的整体进行支护,支护的对象是巷道极限平衡圈内的岩体。根据极限平衡圈理论[15-16],考虑底板破坏的极限平衡圈范围如图14所示。
设W0为巷道开挖宽度,巷道左右侧(符号下标分边取1,2),若 l1max+l2max<W0,则巷道底板成“W”破坏;若l1max+l2max≥W0,巷道底板成反拱形破坏。
当 l1max=l2max=0.5W0时,有
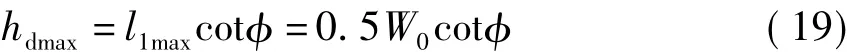
代入(17)可得底板破坏引起巷帮破坏深度为(可作为巷帮锚杆长度确定的依据)
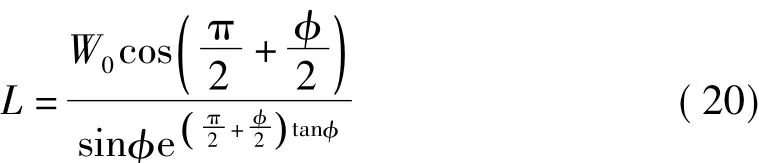
顶板极限平衡拱的高度为

将(20)代入(21),可得顶板极限平衡拱高度为(可作为顶板锚索长度的确定依据)y
lim=
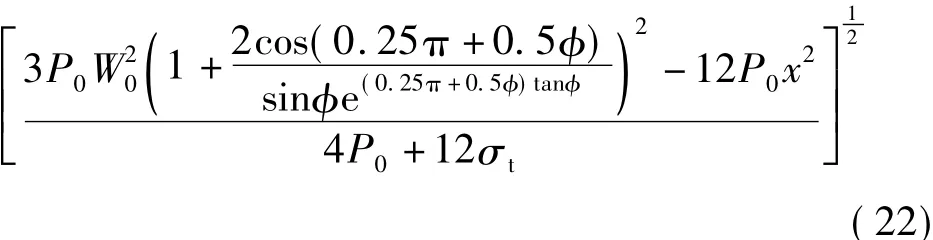

图14 巷道支护的极限平衡圈Fig.14 Limit equilibrium ring of roadway support
4.2 实例分析
以蒋家河煤矿ZF204运输顺槽为例,巷道底板未支护,q=0 MPa;内聚力 c=1.72 MPa;底板容重γ =24 kN/m3; =35°;W0=5.0 m,η =0.9;c*=1.55 MPa;*=32.22°;k=1.68;P0=16.25 MPa.由公式(8)得巷道极限承载力
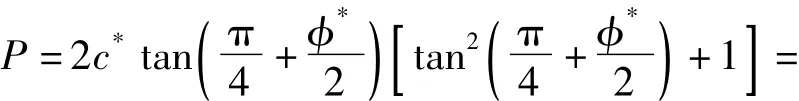
23.99 MPa
而P1=kP0=27.3 MPa>P,故底板破坏。
1)l1max=l2max=0.5W0=2.5 m,巷道底板最大破坏深度hdmax为
hdmax=l1max× cot =3.57 m
2)巷帮破坏深度

3)巷帮底板破坏深度为

4)巷道顶部的平衡拱、极限平衡拱高度
原岩应力P0=16.25 MPa,顶板岩石抗压强度σc=65.32 MPa,抗拉强度 σt=4.25 MPa,巷帮高度hw=3.1 m,巷宽 W0=5.0 m,巷帮破坏深度 L=1.87 m.
两帮稳定时的平衡拱高度

有底板破坏时的极限平衡拱

根据上述计算,巷道底鼓使顶板破坏区高度增加了2.71 m.顶板锚索长度按照极限平衡拱高度取6 m,两帮锚杆长度取2 m.根据工程经验,按照帮部底板破坏深度的70%取底板锚杆长度2.0 m.实践表明,巷道变形量小于10%,巷道在使用期间安全稳定。
5 结论
1)巷道两帮下沉,两帮脚内收,底板中部上升,顶板下沉,形成向巷道中心的收敛变形。巷道底板破坏严重,为挤压流动型底鼓;
2)巷道底板极限承载力随底板内聚力、内摩擦角和折减系数的减小而减小;
3)巷道帮脚底板破坏深度和底板最大破坏深度随巷帮极限平衡区宽度线性增长;
4)巷道两侧最大底板破坏区不重叠时,底板成“W”型破坏;重叠时底板成拱形破坏。底板与两帮和顶板破坏区相互影响,共同形成巷道“极限平衡圈”。
[1] 程远平,俞启香.中国煤矿区域性瓦斯治理技术的发展[J].采矿与安全工程学报,2007,24(4):383 -390.CHENGYuan-ping,YUQi-xiang.Development of regional gas control technology for Chinese coalmines[J].Journal of Mining and Safety Engineering,2007,24(4):383-390.
[2] 周宏伟,谢和平,左建平.深部高地应力下岩石力学行为研究进展[J].力学进展,2005,35(1):91 -99.ZHOU Hong-wei,XIE He-ping,ZUO Jian-ping.Research progress of deep rock mechanics behaviors under high geostress[J].Advances in Mechanics,2005,35(1):91-99.
[3] 李 刚,梁 冰,张国华.高应力软岩巷道变形特征及其支护参数设计[J].采矿与安全工程学报,2009,26(2):183-186.LI Gang,LIANG Bing,ZHANG Guo-hua.Deform ation features of roadway in highly stressed soft rock and design of supporting parameters[J].Journal of Mining and Safety Engineering,2009,26(2):183 -186.
[4] 康红普.软岩巷道底鼓的机理及防治[M].北京:煤炭工业出版社,1993.KANG Hong-pu.The mechanism of floor heave of soft rock tunnel excavation and prevention[M].Beijing:Coal Industry Publishing House,1993.
[5] 陆士良,姜耀东.巷道底鼓的机理和防治[J].中国煤炭,1995(8):13-17.LU Shi-liang,JIANG Yao-dong.The mechanism of floor heave of roadway and the prevention and control[J].China Coal,1995(8):13 -17.
[6] 杨建中.巷道底鼓的机理分析[J].云南冶金,1998,27(4):13-16.YANG Jian-zhong.A study mechanism of tunnel floorheave[J].Yunnan Metallurgy,1998,27(4):13 -16.
[7] 董方庭.巷道围岩松动圈支护理论及其应用技术[M].北京:煤炭工业出版社,2001.DONG Fang-ting.The broken zone support theory andits application technology for surrounding rock of roadway[M].Beijing: China Coal Industry Publishing House,2001.
[8] 姜耀东,赵毅鑫,刘文岗,等.深部开采中巷道底鼓问题的研究[J].岩石力学与工程学报,2004,23(14):2396-2401.JIANG Yao-dong,ZHAO Yi-xin,LIU Wen-gang,et al.Research on floor heave of roadway in deep mining[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(14):2396 -2401.
[9] 康红普,陆士良.巷道底臌机理的分析[J].岩石力学与工程学报,1991,2(4):362 -373.KANG Hong-pu,LU Shi-liang.An analysis on the mechanism of roadway floor heave[J].Chinese Journal of Rock Mechanics and Engineering,1991,2(4):362-373.
[10]初明祥,王清标,夏均民.采空侧巷道底鼓形成机制与防治技术研究[J].岩土力学,2011(S2):413-417.CHU Ming-xiang,WANG Qing-biao,XIA Jun-min.Study of formation mechanism of floor heave at goaf side of roadway and prevention technology[J].Rock and Soil Mechanics,2011(S2):413 -417.
[11]王卫军,冯 涛.加固两帮控制深井巷道底臌的机理研究[J].岩石力学与工程学报,2005,24(5):808-811.WANG Wei-jun,FENG Tao.Study on mechanism of reinforcing sides to control floor heave of extraction opening[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(5):808 -811.
[12]刘泉声,刘学伟,黄 兴,等.深井软岩破碎巷道底臌原因及处置技术研究[J].煤炭学报,2013,38(4):566-571.LIU Quan-sheng,LIU Xue-wei,HUANG Xing,et al.Research on the floor heave reasons and supporting measures of deep soft-fractured rock roadway[J].Journal of China Coal Society,2013,38(4):566 -571.
[13]张红军,李海燕,李术才,等.深部软岩巷道围岩变形机制及支护技术研究[J].采矿与安全工程学报,2015,32(6):955 -962.ZHANG Hong-jun,LI Hai-yan,LI Shu-cai,et al.Deformation mechanism of surrounding rock and support technology in deep soft rock roadway[J].Journal of Mining and Safety Engineering,2015,32(6):955 -962.
[14]袁 亮,薛俊华,刘泉声,等.煤矿深部岩巷围岩控制理论与支护技术[J].煤炭学报,2011,36(4):535-543.YUAN Liang,XUE Jun-hua,LIU Quan-sheng,et al.Surrounding rock stability control theory and support technique in deep rock roadway for coal mine[J].Journal of China Coal Society,2011,36(4):535 -543.
[15]黄庆享,刘玉卫.巷道围岩支护的极限自稳平衡拱理论[J].采矿与安全工程学报,2014,31(3):354 -358.HUANG Qing-xiang,LIU Yu-wei.Ultimate self-stable arch theory in roadway support[J].Journal of Mining and Safety Engineering.2014,31(3):354 -358.
[16]黄庆享,郑 超.巷道支护的自稳平衡圈理论[J].岩土力学,2016,37(5):1231 -1236.HUANG Qing-xiang,ZHENG Chao.Theory of selfstable ring in roadway support[J].Rock and Soil Mechanics,2016,37(5):1231 -1236.
[17]郑颖人,赵尚毅,李安洪,等.有限元极限分析法及其在边坡工程中的应用[M].北京:人民交通出版社,2011.ZHENG Ying-ren,ZHAO Shang-yi,LI An-hong,et al.FEM limit analysis and its application in slope engineering[M].Beijing:China Communications Press,2011.
[18]袁 维,李小春,王 伟,等.一种双折减系数的强度折减法研究[J].岩土力学,2016,37(8):2222 -2230.YUAN Wei,LI Xiao-chun,WANG Wei,et al.Study on strength reduction method based on double reduction parameters[J].Rock and Soil Mechanics,2016,37(8):2222-2230.
[19]谢定义,姚仰平,党发宁.高等土力学[M].北京:高等教育出版社,2008.XIE Ding-yi,YAO Yang-ping,DANG Fa-ning.Advanced soil mechnics[M].Beijing:Higher Education Press,2008.
[20]钱鸣高,石平五,许家林.矿山压力与岩层控制[M].徐州:中国矿业大学出版社,2010.QIAN Ming-gao,SHI Ping-wu,XU Jia-lin.Mining pressure and strata control[M].Xuzhou:China University of Ming and Techology Press,2010.

