Boost变换器的环路补偿设计
(广西大学 电气工程学院,广西 南宁 530004)
1 引言
一直以来,开关电源中环路的补偿和计算都是一个难点问题,也是工程应用中需要重点关注的部分。在开关电源的设计中需要使电源拥有一个良好的静态指标和动态指标,这就要求在人们除了对主电路进行精心计算还需要一个良好的反馈控制系统,而补偿网络直接影响着反馈回路的性能因此补偿回路的设计非常重要。由于在开关变换器中电感的等效串联电阻和输出滤波电容的等效串联电阻ESR会给变换器引入一个右半平面的零点,从而对整个环路的设计带来影响,因此分析这两个电阻对环路所带来的影响有着重要的研究意义[1-2]。
本次设计是以传统的Boost变换器为例,来研究非线性器件中的等效串联电阻对变换器环路所带来的影响,并应用小信号分析法建立模型,最后利用仿真分析来验算系统的合理性[3]。
在开环增益为1时,系统的总开环相位延迟必须小于360°。在截止频率出开环相位延迟小于360°的角度称为相位裕量。为使系统在最恶劣情况下仍能稳定,要求系统至少有35°到45°的相位裕量。据此原则进行环路设计,可以实现在温度发生变化或负载突变时都能满足稳定调节[4-5]。
2 本次设计的主要技术指标
输入电压:Vin=10V;输出电压Vo=20V;开关频率f=50kHz;电感L=20uH,RL=0.005Ω;电容C=1000uF,RC=0.005Ω,R1=10kΩ,R2=10kΩ。

图1 Boost变换器的原理图
其负反馈控制框图如图2所示。
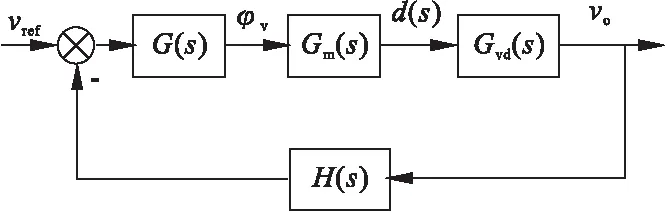
图2 Boost变换器的闭环控制系统
其中Gvd(s)为变换器的占空比d(s)到输出电压Vo(s)的传递函数,Gm(s)为PWM脉宽调制器的传递函数,H(s)表示反馈网络的传递函数,G(s)为补偿网络的传递函数[6]。
(1)

PWM脉宽调制信号的传递函数为:
Gm(s)=1/Vm
(2)
反馈网络的传递函数为:
H(s)=R2/(R1+R2)
(3)
因此Boost变换器的回路增益传递函数为:
(4)
由式(4)可以看出Boost变换器的传递函数存在一个右半平面的零点,为了避免此零点引起过多的相移,一般取环路带宽为其频率的1/4~1/5,此处取1/5即fg=10kHz[7]。
3 Boost变换器补偿网络的设计
将Boost变换器的参数数据代入式(4)中得到:
(5)
用Matlab来分析不加补偿器时Boost变换器的Bode图,如图3所示。
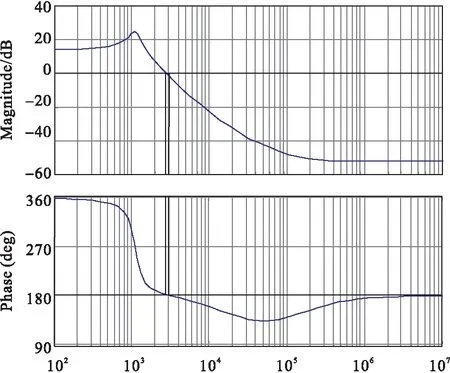
图3 不加补偿网络的Bode图
从上图中可以看出在低频时增益保持不变,整个增益以-40dB/decade穿越0dB线,穿越频率fc=2.76kHz。相位裕度为2.07°,显然系统是一种不稳定的状态,需要添加补偿网络来提高系统的稳定性,所添加的补偿网络在fg处应该提供一个+20dB/decade的斜率,采用双零双极点补偿电路,如图4所示[8]。
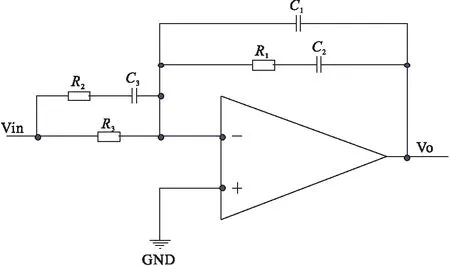
图4 补偿电路
传递函数:
(6)
补偿网络为有源超前-滞后网络,有两个零点、三个极点(R3≥R2,C2≥C1)。零点频率为:
(7)
极点频率为:
(8)
设置控制器的两个零点均为fz1=fz2=0.5fp0=563Hz;第一个极点fp1用来抵消右半平面的零点fz,fp1=fz=19.9kHz;第二个极点fp2用来增加高频衰减率,其值为fp2=10fc=27.6kHz。设R1=10kΩ,在高频段的电压放大倍数为Av2=(fp1/fc)*42=R1/R2=300,可得R2=33Ω,将上述参数代入到式(7)、(8)中得出相应为参数为:
C2=28.3nF,C3=0.242μF,C1=577pF,R3=1.2kΩ
补偿函数为:
(9)
补偿后的系统Bode图如图5所示。

图5 补偿后的Bode图
从图中可以看出系统的相位裕度为68.4dB,穿越频率为6.09kHz。此时整个系统是处于稳定的状态。
4 结论
本文利用Boost变换器的小信号传递函数,将控制理论与变换器的环路补偿相结合,通过设计合适的相位裕量来保证开关电源的稳定性,其过程经实验证明具有较好的通用性,对实际电路中参数的选取具有很好的指导意义。

