多向荷载作用下隔离矿柱采场矿壁受力分析

过江，赵岩，张为星，戴兴国，谢学斌



多向荷载作用下隔离矿柱采场矿壁受力分析

过江，赵岩，张为星，戴兴国，谢学斌

(中南大学 资源与安全工程学院，湖南 长沙，410083)

为确定梯形侧向荷载和垂直荷载共同作用下矿壁的应力分布，基于弹性力学平面应变假设，建立矿壁力学模型进行应力求解。通过模型分析，确定矿壁合理宽度，分析可能发生破坏的形式，提出矿壁稳定性的控制措施。研究结果表明：初始侧向荷载对水平应力、垂直应力和剪应力均有影响，初始垂直荷载0只影响垂直应力；水平应力最大值和最小值不随宽度改变而改变；剪应力沿矿壁中心轴呈对称分布，在中心位置达到最大值。当矿壁宽度较窄时，在充填体一侧会出现拉应力，在矿壁的采空区侧的底端出现垂直压应力最大值。结合冬瓜山工程实例，计算出矿壁宽度需大于3.5 m，现场工程选择4 m宽矿壁进行开采，矿壁稳定性较好。

多向荷载；稳定性；宽度设计；力学模型

随着长期大范围的开采，浅部有色矿产资源已接近枯竭，矿床的开采逐渐向深部发展。在进行深部金属矿床开采时，原岩的初始应力遭到破坏，应力重新分布。矿柱作为支撑采空区的重要结构，其稳定性显得至关重要。矿柱一旦失稳，就可能造成顶板围岩冒落、充填体垮落，直接影响生产，甚至造成设备损毁与工作人员受伤等重大事故发生。目前，国内学者对矿柱稳定性进行了大量研究，如：姜立春等[1]基于动态强度折减法，揭示了矿柱渐进失稳演变规律；宋卫东等[2]对矿柱稳定性影响因素敏感性进行分析，得出条形矿柱布置下矿柱宽度影响最大的结构；付建新 等[3]基于弹塑性力学对存在初始几何缺陷的超高矿柱的挠度和内力进行分析，结果表明矿柱的附加挠度随着初始挠度和压力比的增加而增加；李江腾等[4]应用断裂力学讨论硬岩矿柱初始裂纹在上覆岩层作用下贯通形成层状结构的机理，为合理布置采场提供了依据；王连国等[5−6]将突变理论应用在煤柱失稳、矿壁失稳等采场稳定性的问题上，均取得了较好的效果；陈庆发等[7−8]构建了顶板−矿柱三维空间力学模型，分析了对称协同开采人工矿柱的失稳机制；陈顺满等[9]利用正交极差分析方法对矿柱稳定性影响因素进行敏感性分析；程海勇等[10]利用统计学原理计算矿柱厚度影响因素的变异系数，并进行权重分析，最终获得矿柱的合理宽度；王晓军等[11]根据普氏地压学说理论，通过分析得出回采跨度与回采深度对人工矿柱合理宽度的影响；赵国彦等[12−13]通过数值模拟对房柱法的矿柱合理尺寸、境界矿柱的稳定性进行研究，均取得较好效果。总体来说，学者们通过各种方法对矿柱稳定性进行了研究，也取得了不错的效果，但对如何建立矿柱的弹性力学模型还研究较少。曹帅等[14]基于弹性力学建立金属矿山阶段嗣后充填胶结充填体矿柱力学模型，对侧向三角形荷载胶结充填体矿柱进行力学分析，但未考虑梯形荷载的情况。充填法采矿不仅有效控制地表位移，也可以实现对尾砂的充分利用。对采空区进行充填后，充填体不能接顶导致充填体不能直接承受上部荷载，当上部岩体完整性较差时，可能发生冒落导致充填体对矿柱产生梯形侧向荷载。本文作者基于弹性理论，对梯形侧向荷载分布的矿柱进行求解，以冬瓜山铜矿工程为实例，对计算所得结果进行工程实际验证，说明结果的合理性。

1 工程概况

冬瓜山铜矿床位于安徽省铜陵市狮子山矿田内，是我国典型的深埋矿床，主矿体长1 820 m，平均宽度为500 m。矿体赋存标高为−1 010~−690 m，但大部分位于−730 m以下，最大厚度为100.7 m，最小厚度为1.13 m，平均厚度为20~50 m。矿体总体走向北东35°，倾向与背斜两翼产状一致，分别倾向北西和南东，平均倾角为20°，最大倾角为40°，图 1所示为−730 m地质及采场布置情况。

冬瓜山矿床的主要构造为青山背斜，断层有近南北向、东西向、北东向3组，多为张性、张扭性或压性断裂，断裂带倾角大部分大于70°，对主矿体无明显的破坏作用。矿体主要由铜矽卡岩、含铜磁黄铁矿、含铜蛇纹岩和含铜黄铁矿等组成，矿体构造简单，节理裂隙不发育，岩性坚硬，力学强度高、稳定性好。矿体顶板为黄龙、船山组大理岩和矽卡岩，底板为砂岩、粉砂岩以及闪长岩。为实现安全、高效、低成本的回采，采用预留隔离矿柱阶段空场嗣后充填采矿方法进行回采，要求沿矿体走向方向每隔100 m划分 1个盘区，盘区之间留设隔离矿柱以确保矿体回采的安全性以及盘区之间开采相互独立。在盘区内每隔 18 m沿垂直矿体走向方向布置矿房与矿柱，首先采用隔一采一的方式进行矿房回采，对回采完毕的矿房进行全尾砂胶结充填，然后回采矿柱，回采完毕后进行全尾砂充填。随着铜矿矿产资源开采殆尽，为了充分提高矿产资源采出率，需要对隔离矿柱进行开采。

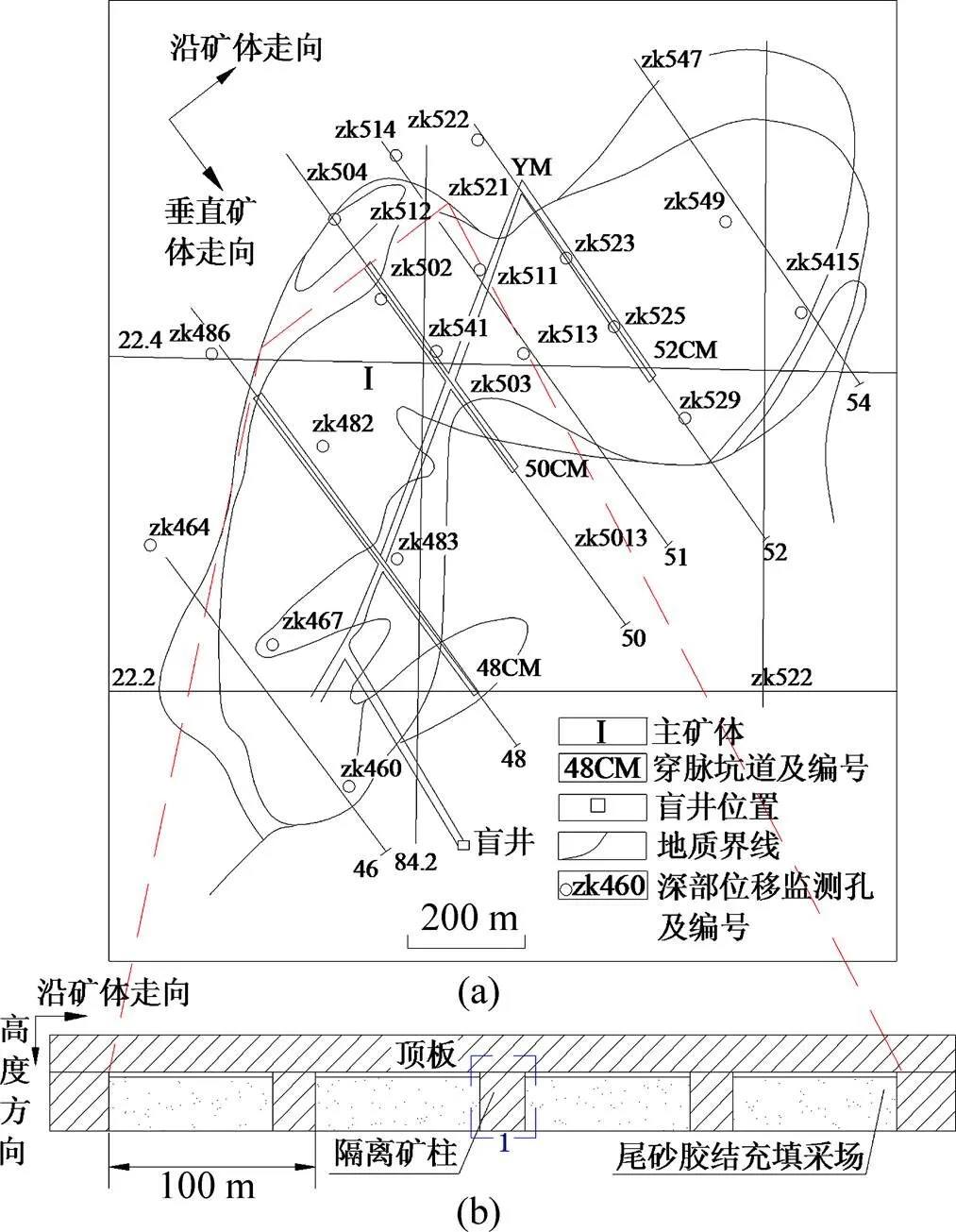
(a) −730 m地质图；(b) 采场布置剖面图

隔离矿柱是盘区大范围矿产资源回收并充填完毕后的剩余资源，虽然大部分开采区岩体完整性良好，但存在部分开采区岩体完整性较差现象，尤其是50线以北构造节理发育，不仅破坏了井巷围岩，而且存在充填体上部顶板岩体冒落现象，如何有效回收隔离矿柱资源，创造经济效益，是矿山面临的主要问题。

2 矿壁力学模型

2.1 力学模型的确定

在弹性力学理论中，一般将横截面积不沿长度变化，在柱面上受平行于横截面积且不沿长度变化的面力或约束，同时体力也平行于横截面积且不沿长度变化的空间问题简化为平面问题。为了满足弹性力学的基本假定，进行如下假设：矿壁是连续的、均匀的、各向同性的完全弹性体，而且由于形变和位移的尺寸完全小于矿壁的尺寸，所以，其满足小变形假定[15]。

图2(a)所示为对图1标注1位置采用大直径深孔后退式侧向崩矿对隔离矿柱进行回采图，图2(b)所示为落矿后矿壁的力学模型。图2 中：为矿壁重度；为矿壁高度；为矿壁宽度；为初始侧向荷载；为侧向压力系数；1为充填体重度；0为初始垂直荷载。

(a) 隔离矿柱回采；(b) 矿壁力学模型

2.2 力学模型求解

基于基本假设和充填体侧荷载的分布形式，可知左侧边界是关于的一次函数且存在常数项，故采用弹性力学半逆解法，并设

反推可得应力函数为

应力函数的应满足相容方程：

将式(2)代入式(3)得

经过积分计算得到()，1()和2()的函数形式为

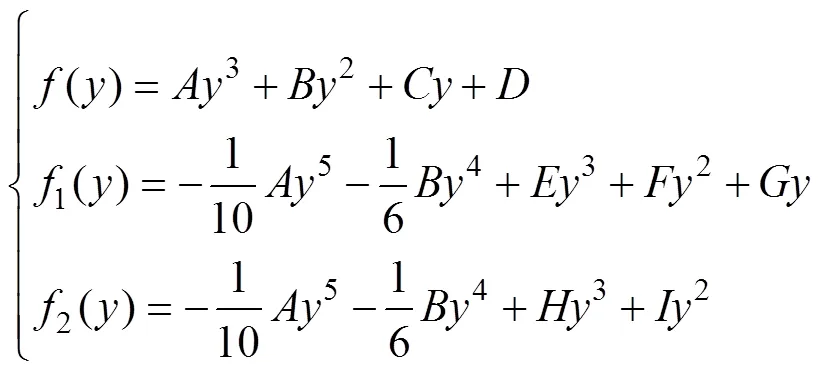
将式(5)代入式(2)得应力函数：

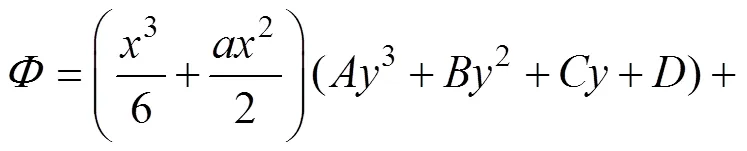
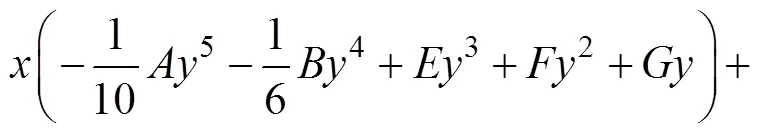
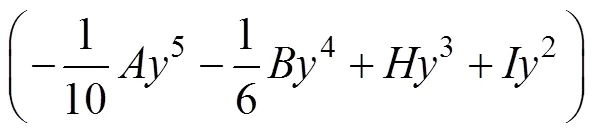
在只考虑自重的影响下，f=，f=0，所以，应力分量的计算可以表示为

将式(6)代入式(7)得应力分量

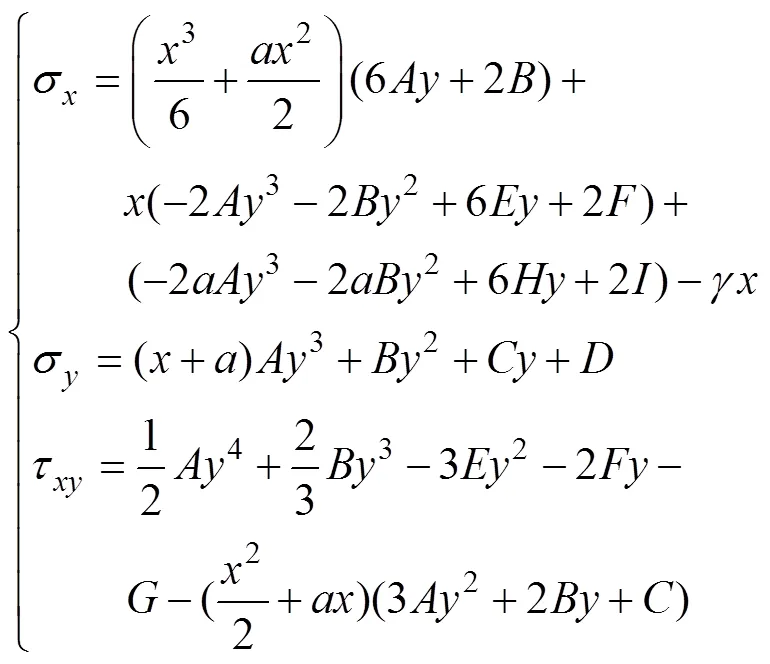
式中：σ为矿壁水平应力；σ为矿壁垂直应力；τ为矿壁剪应力；，，，，，，，，和为方程的待定系数。

2.3 确定边界条件

由于矿体顶板为缓倾斜状态，为了荷载计算方便假设顶板水平。由于矿壁高度远大于宽度，所以，左、右两侧为主边界应完全满足边界条件，此时，上、下两侧不能完全满足边界条件，所以，引用圣维南定 理[15]用积分的应力边界条件代替，使边界条件得到近似的满足。

在深部回采过程中，由于埋深较深的矿壁承受的压力较大，且顶板稳定性较差，节理部分发育，所以，将矿壁顶端简化为只受水平约束，底端简化为只受固定端约束。通过结构力学位移法可以求解出，顶端和底部的支座反力Ft与Fb分别[16]为：

1) 左侧边界条件，在靠近充填体一侧

2) 右侧边界条件，在靠近采空区一侧水平应力与剪应力均为0，即

3) 上部边界条件，在矿壁顶部的垂直应力与剪应力分别为：

4) 下部边界条件，在矿壁底部的垂直应力与剪应力分别为：

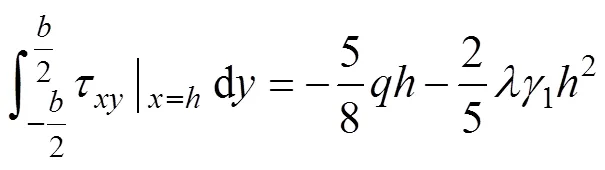
将式(8)代入式(11)~(17)，最终得到矿壁的应力分量计算结果为

由式(18)可见：初始侧向荷载对水平应力、垂直应力和剪应力均有影响，初始垂直应力0只影响垂直应力；水平应力是一个与高度无关的函数，所以，水平应力不随高度改变而改变；当一定时，剪应力是一个关于的偶函数。

3 矿壁合理宽度优化

3.1 计算参数的确定

表1所示为矿岩物理力学参数。

表1 矿岩物理力学参数

在稳定性较差的岩体中开挖，顶板岩体在一定范围内发生冒落。工程实践结果表明，冒落后会在顶部形成1个包含塑性区域的平衡拱，也称为普氏拱。

由普氏理论可知无支护条件下塑性区厚度p的计算公式为[17]

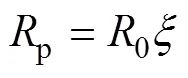
塑性区半径修正系数为

等效开挖半径[18]为

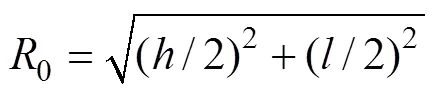
顶板处的垂直自重应力为

式中：为塑性区半径修正系数；0为等效开挖半径；为顶板处的垂直自重应力；t为顶板岩体黏聚力；为顶板岩体内摩擦角；为开挖长度；2为顶板岩体重度；0为开采深度。

3.1.1 矿壁的初始侧向荷载的确定

对采空区进行充填以后，由于充填体没有接顶所以不能直接承受顶部的压力，由普氏理论可知充填体上部冒落岩体自重为

初始侧向荷载为

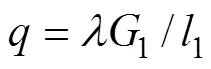
将式(19)~(23)代入式(24)，得出矿壁受到的初始侧向荷载的计算公式为

式中：p1为充填体区域塑性区的等效半径；1为充填体的长度；1为充填体上部冒落岩体对充填体的 压力。

3.1.2 矿壁受到的垂直应力0的确定

矿房矿柱开挖后使用全尾砂进行充填，由普氏理论可知对隔离矿柱开采前，形成的普氏拱如图3所示。由于充填体未接顶，不能直接承受上部岩体重力，所以，隔离矿柱承受上部相同数字对应的塑性区岩体自重。

隔离矿柱承担的岩体自重为

隔离矿柱开挖后，塑性区岩体自重由预留下的两侧矿壁承担，各个矿壁承担的均布荷载为

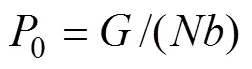
把式(19)～(22)、式(26)代入式(27)，得出矿壁受到的初始垂直荷载0的计算公式为

式中：p0为沿矿体走向长度塑性区的等效半径；为隔离矿柱上部塑性区岩体的重力；0为剖面上沿矿体走向长度；2为隔离矿柱宽度；为承压的矿壁个数。

图3 塑性区分布图

Fig. 3 Plastic zone distribution

3.1.3 侧向压力系数的确定

充填体对矿壁的侧向压力，采用朗金土压力理论进行计算，其主动侧向压力系数为

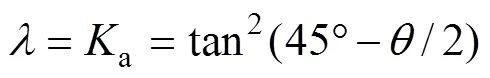
式中：a为充填体对矿壁的主动侧向压力系数；为充填体的内摩擦角。

3.2 应力分量结果分析

由于求得的应力函数复杂，故本文针对=25 m高的矿壁，宽度按3，4和5 m 3个水平划分通过图像对应力进行分析,根据矿山实际情况，取参数= 730 m，0=400 m，1=78 m，2=22 m，=2。

3.2.1 垂直应力分析

图4所示为矿壁不同高度垂直应力分布图。由图4可见：不同高度矿壁的垂直应力关于点(0，0)对称，从式(18)计算得0即为−0；当矿壁宽度较窄时，矿壁在充填体一侧可能会出现拉应力，从式(18)分析拉应力是由侧向荷载引起的；在矿壁的采空区侧的底端出现垂直压应力最大值，是确定矿壁合理宽度的关键 因素。

(a) b=3 m；(b) b=4 m；(c) b=5 m

3.2.2 水平应力分析

图5所示为矿壁不同高度水平应力分布图。由图5可见：矿壁靠近采空区处对应的水平应力为0 Pa；而在靠近充填体侧，矿壁水平应力在底端达到最大值；在高度一定的情况下，在充填体侧水平应力随矿壁高度增加而增加，且最大值和最小值不随宽度的改变而改变。

(a) b=3 m；(b) b=4 m；(c) b=5 m

3.2.3 剪应力分析

图6所示为矿壁不同高度剪应力分布图。由图6可见：矿壁在采空区侧和充填体侧的剪应力为0 MPa，沿矿壁中心轴呈对称分布，在中心位置达到最大值；在宽度一定的情况下，剪应力随高度的增加而增加，在矿壁底端达到最大值；在高度一定的情况下，剪应力随宽度增加而减小。

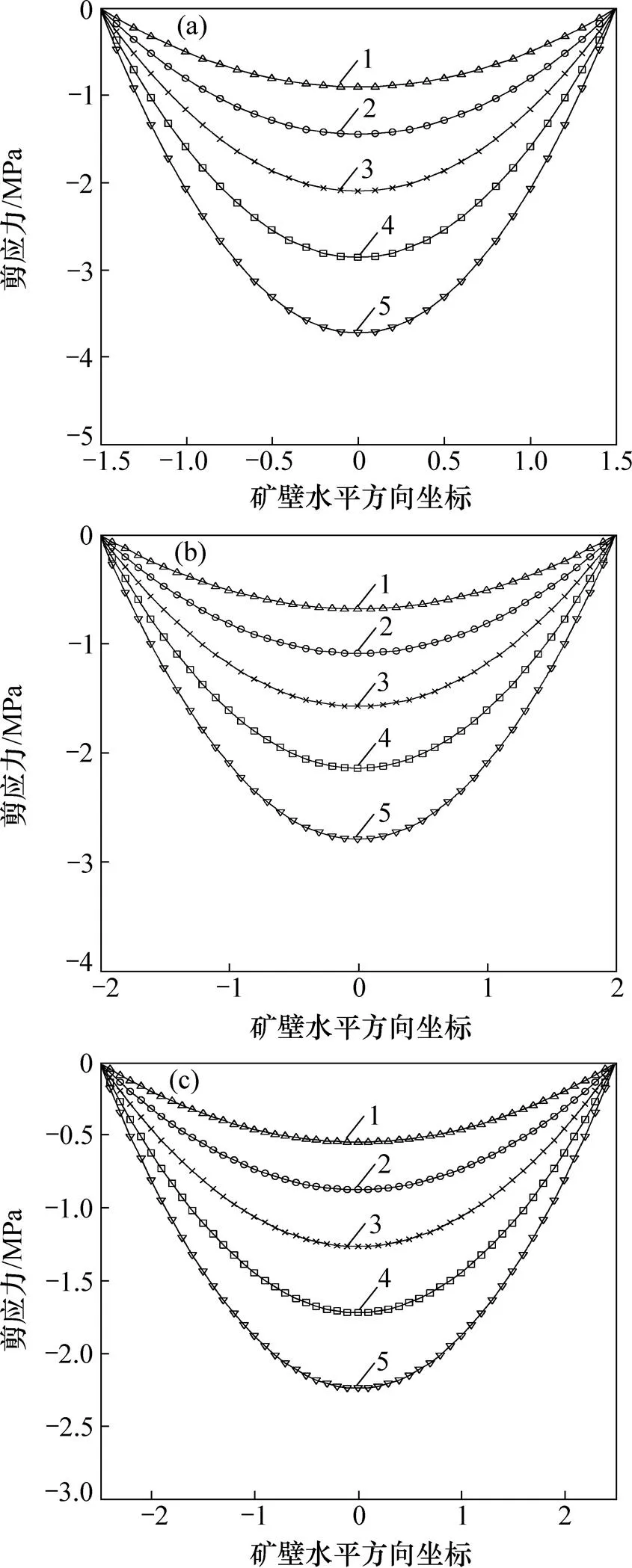
(a) b=3 m；(b) b=4 m；(c) b=5 m

3.3 矿壁稳定性及宽度优化

由应力分量结果分析可知：垂直应力在矿壁底部达到最大，且在靠近充填体侧可能出现拉应力；水平应力随矿壁充填体高度增加而增大，在底端达到压应力最大值；剪应力在矿壁底端中部达到最大值。不同高度的隔离矿柱预留矿壁宽度不同将会导致不同的受力情况，矿壁过窄将会导致矿壁失稳，过宽又会导致资源浪费。为了避免浪费，充分回收矿产资源，矿壁宽度应满足：

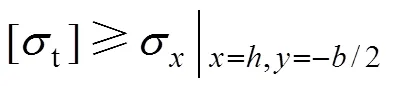
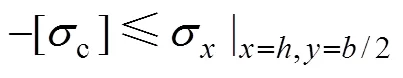
由霍克−布朗岩体强度准则[19−20]可知：

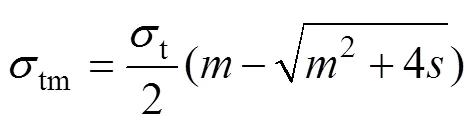
式中：f为完整岩体的抗剪强度；1与3为岩体破坏时的最大最小主应力；c为完整岩块的抗压强度；为霍克布朗常数；为表征岩体质量量纲一的量；tm为岩体单轴抗拉强度；t为完整岩块的抗拉强度。

根据矿山的实测数据，取参数c=190.3 MPa，t=17.1 MPa，=6.9，=0.302。当3=0时，可求得矿壁的岩体抗压和抗拉强度分别为[t]=0.74 MPa，[c]=104.5 MPa，观察图7发现矿壁水平应力和剪应力较小，矿壁宽度主要由式(30)和式(31)控制，经计算分别得≥3.4 m，≥3.5 m。结合矿壁的受力情况分析，矿壁可能发生屈曲失稳和整体倾覆破坏，可采取相关措施杜绝可能存在的安全隐患，确保开采的安全。根据前面的分析结果，主要从以下个2个方面考虑。

1—式(30)；2—式(31)；3—式(32)；4—式(33)。

1) 加强顶板管理。在进行回采作业前，对区域内硐室、巷道顶板稳定性状况进行勘查、评估并确认，对区域内发现的如脱钎、离层及有裂缝的不稳定顶板进行加固处理。

2) 在底部漏斗施工及爆破回采阶段，需注意底部矿壁的维持。在回采过程中不允许出空，应预留一定高度的矿石层以起到护壁与垫层的作用，避免中间回采过程矿壁底部压应力过大发生破坏。

3.4 工程实际验证

根据理论分析，现场留设4 m宽薄矿壁进行开采，采用 CMS 空区精密探测技术(3D Cavity Monitoring System)对空区进行扫描，并使用BGK－A3多点位移计对隔离矿柱采场进行监测，以反映回采过程矿壁变形，分析矿壁稳定性。

由Optech制造的CMS是标准采矿作业中危险和难以接近的空区的理想扫描解决方案[21]。CMS检测主要使用360°旋转扫描头进行集成激光扫描收集距离和角度数据。矿山G6隔离矿柱试验采场回采后，G6 CMS空区扫描结果如图8所示。

由图8可见：隔离矿柱采场两侧矿壁顶部保持完整，未发现倾覆破坏的现象，矿壁底部未发生大的断裂，承压性能良好；采空区顶板未发现冒落，多点位移计监测到顶板最大位移为34 mm，位移变化量在控制范围内；空区扫描及出矿均未发生充填体大量混入现象，充填体稳定性良好。通过工程验证，整个空区稳定性较好，与理论计算结果基本一致。

图8 G6 CMS空区扫描

4 结论

1) 初始侧向荷载对水平应力、垂直应力和剪应力均有影响，初始垂直荷载0只影响垂直应力。

2) 当矿壁宽度较窄时，矿壁在充填体一侧会出现拉应力，在矿壁的采空区侧的底端出现垂直压应力最大值；在高度一定的情况下，在充填体侧水平应力随矿壁高度增加而增加，且最大值和最小值不随宽度的改变而改变；矿壁剪应力沿矿壁中心轴呈对称分布，在中心位置达到最大值；在宽度一定的情况下，剪应力随高度的增加而增加，在矿壁底端达到最大值；在高度一定的情况下，剪应力随宽度增加而减小。

3) 结合冬瓜山工程实例，分析得出矿壁宽度主要受充填体侧拉应力和采矿区侧压应力控制，计算出矿壁宽度需大于3.5 m，并提出可能发生破坏的形式以及矿壁稳定性控制措施。为了保证安全，现场工程选择4 m宽矿壁进行开采，监测得到整个采场稳定性较好，隔离矿柱G6等3个试验采场的成功回采验证了此力学模型的合理性，为盘区后续隔离矿柱采场回采奠定了基础。

[1] 姜立春, 魏叙深, 吴爱祥. 基于动态强度折减法矿柱渐进失稳演变规律[J]. 中南大学学报(自然科学版), 2016, 47(2): 621−627. JIANG Lichun, WEI Xushen, WU Aixiang. Gradual evolution law of pillar based on dynamic strength reduction method[J]. Journal of Central South University(Science and Technology), 2016, 47(2): 621−627.

[2] 宋卫东, 曹帅, 付建新, 等. 矿柱稳定性影响因素敏感性分析及其应用研究[J]. 岩土力学, 2014, 35(S1): 271−277. SONG Weidong, CAO Shuai, FU Jianxin, et al. Sensitivity analysis of impact factors of pillar stability and its application[J]. Rock and Soil Mechanics, 2014, 35(S1): 271−277.

[3] 付建新, 曹帅, 宋卫东, 等. 考虑初始缺陷的超高矿柱蠕变分析及失稳滞后时间研究[J]. 中国矿业大学学报, 2017, 46(2): 279−284.FU Jianxin, CAO Shuai, SONG Weidong, et al. Creep analysis and delay time of instability of ultrahigh pillar considering initial imperfections[J].Journal of China University of Mining, 2017, 46(2): 279−284.

[4] 李江腾, 曹平. 硬岩矿柱纵向劈裂失稳突变理论分析[J]. 中南大学学报(自然科学版), 2006, 37(2): 371−375. LI Jiangteng, CAO Ping. Analysis of pillar stability in hard rock mass by longitudinal splitting based on catastrophe theory[J]. Journal of Central South University(Science and Technology), 2006, 37(2): 371−375.

[5] 王连国, 缪协兴. 基于尖点突变模型的矿柱失稳机理研究[J]. 采矿与安全工程学报, 2006, 23(2): 137−140. WANG Lianguo, MIAO Xiexing. Study of mechanism of destabilization of the mine pillar base on a cusp catastrophic model[J]. Journal of Mining & Safety Engineering, 2006, 23(2): 137−140.

[6] 王贻明, 徐恒, 吴爱祥, 等. 基于尖点突变模型的临时矿壁系统失稳机制及矿壁厚度优化[J]. 采矿与安全工程学报, 2016, 33(4): 662−667, 675. WANG Yiming, XU Heng, WU Aixiang, et al. Study on instability mechanism and thickness optimization of temporary ore wall based on cusp catastrophe model[J]. Journal of Mining & Safety Engineering, 2016, 33(4): 662−667, 675.

[7] 陈庆发, 古德生, 周科平, 等. 对称协同开采人工矿柱失稳的突变理论分析[J]. 中南大学学报(自然科学版), 2012, 43(6): 2338−2342. CHEN Qingfa, GU Desheng, ZHOU Keping, et al. Analysis of catastrophe theory for artificial pillar instability in symmetric synergistic mining[J]. Journal of Central South University(Science and Technology), 2012, 43(6): 2338−2342.

[8] 谢学斌, 邓融宁, 董宪久, 等. 基于突变和流变理论的采空区群系统稳定性[J]. 岩土力学, 2018, 39(6): 1963−1972. XIE Xuebin, DENG Rongning, DONG Xianjiu, et al. Stability of goaf group system based on catastrophe theory and rheological theory[J]. Rock and Soil Mechanics, 2018, 39(6): 1963−1972.

[9] 陈顺满, 吴爱祥, 王贻明, 等. 深部回采矿柱稳定性影响因素分析及其应用[J]. 中南大学学报(自然科学版), 2018, 49(8): 2050−2057. CHEN Shunman, WU Aixiang, WANG Yiming, et al. Analysis of influencing factors of pillar stability and its application in deep mining[J]. Journal of Central South University(Science and Technology), 2018, 49(8): 2050−2057.

[10] 程海勇, 吴爱祥, 韩斌, 等. 露天−地下联合开采保安矿柱稳定性[J]. 中南大学学报(自然科学版), 2016, 47(9): 3183−3192. CHENG Haiyong, WU Aixiang, HAN Bin, et al. Stability of safety pillars in opencast-underground combined mining[J]. Journal of Central South University(Science and Technology) , 2016, 47(9): 3183−3192.

[11] 王晓军, 冯萧, 杨涛波, 等. 深部回采人工矿柱合理宽度计算及关键影响因素分析[J]. 采矿与安全工程学报, 2012, 29(1): 54−59. WANG Xiaojun, FENG Xiao, YANG Taobo, et al. Reasonable width calculation and analysis of artificial pillar in deep mining[J]. Journal of Mining & Safety Engineering, 2012, 29(1): 54−59.

[12] 赵国彦, 周礼, 李金跃, 等. 房柱法矿柱合理尺寸设计及矿块结构参数优选[J]. 中南大学学报(自然科学版), 2014, 45(11): 3943−3948. ZHAO Guoyan, ZHOU Li, LI Jinyue, et al. Reasonable pillar size design and nugget structural parameters optimization in room-and-pillar mining[J]. Journal of Central South University(Science and Technology), 2014, 45(11): 3943−3948.

[13] 李元辉, 南世卿, 赵兴东, 等. 露天转地下境界矿柱稳定性研究[J]. 岩石力学与工程学报, 2005, 24(2): 278−283. LI Yuanhui, NAN Shiqing, ZHAO Xingdong, et al. Stability of boundary pillars for transition from open pit to underground mining[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(2): 278−283.

[14] 曹帅, 杜翠凤, 谭玉叶, 等. 金属矿山阶段嗣后充填胶结充填体矿柱力学模型分析[J]. 岩土力学, 2015, 36(8): 2370−2376. CAO Shuai, DU Cuifeng, TAN Yuye, et al. Mechanical model analysis of consolidated filling pillar using stage-delayed backfill in metal mines[J]. Rock and Soil Mechanics, 2015, 36(8): 2370−2376.

[15] 徐芝纶. 弹性力学[M]. 5版. 北京: 高等教育出版社, 2016: 10−84. XU Zhilun. Elasticity[M]. 5th ed. Beijing: Higher Education Press, 2016: 10−84.

[16] 朱慈勉, 张伟平. 结构力学(上册)[M]. 北京: 高等教育出版社, 2009: 168−194. ZHU Cimian, ZHANG Weiping. Structural mechanics(volume one)[M]. Beijing: Higher Education Press, 2009: 168−194.

[17] 赵文, 曹平, 章光. 岩石力学[M]. 长沙: 中南大学出版社, 2010: 162−166. ZHAO Wen, CAO Ping, ZHANG Guang. Rock mechanics[M]. Changsha: Central South University Press, 2010: 162−166.

[18] 过江, 冯永菲. 深部回采矿柱失稳的尖点突变理论分析及宽度优化[J]. 中国安全生产科学技术, 2017, 13(7): 111−116. GUO Jiang, FENG Yongfei. Cusp catastrophe theory analysis and width optimization on instability of pillar in deep mining[J]. Journal of Safety Science and Technology, 2017, 13(7): 111−116.

[19] 何江达, 张建海, 范景伟. 霍克−布朗强度准则中，参数的断裂分析[J]. 岩石力学与工程学报, 2001, 20(4): 432−435. HE Jiangda, ZHANG Jianhai, FAN Jingwei. Fracture analysis of,parameters in HOEK−BROWN criteria[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(4): 432−435.

[20] 王文星. 岩体力学[M]. 长沙: 中南大学出版社, 2004: 60−68. WANG Wenxing. Rocks mechanics[M]. Changsha: Central South University Press, 2004: 60−68.

[21] HUANG Zhiguo, DAI Xingguo, DONG Longjun. Buckling failures of reserved thin pillars under the combined action of in-plane and lateral hydrostatic compressive forces[J]. Computers and Geotechnics, 2017, 87: 128−138.

Stress analysis of mine wall in panel barrier pillar-stope under multi-directional loads

GUO Jiang, ZHAO Yan, ZHANG Weixing, DAI Xingguo, XIE Xuebin

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

In order to determine the stress distribution of the mine wall under the trapezoidal lateral load and vertical load, a mechanical model of the mine wall was established and analyzed based on the elastic plane strain assumption. Using the model, the reasonable width of the mine wall was determined, the possible forms of failure were analyzed, and the controls related to the mine wall stability were proposed. The results show that the initial lateral loadaffects the horizontal stress, the vertical stress and the shear stress, and the initial vertical load0only affects the vertical stress. The maximum and the minimum of horizontal stress do not change with the width. The shear stress is symmetrically distributed along the central axis of the mine wall and the maximum appears in the center of the mine wall. When the mine wall is small, the tensile stress appears on the side of filling body. The maximum vertical compressive stress appears at the bottom on the side of the cavity. According to the cases of Dongguashan copper mine, the width should be more than 3.5 m. The mine wall with 4 m in width is selected for on-site engineering, and the mine wall stability is in good condition.

multi-directional loads; stability; width design; mechanical model

10.11817/j.issn.1672−7207.2018.12.016

TD 323

A

1672−7207(2018)12−3020−09

2017−12−20；

2018−01−25

国家自然科学基金资助项目(51774321)(Project(51774321) supported by the National Natural Science Foundation of China)

过江，副教授，从事采矿与充填技术研究；E-mail：guojiang@csu.edu.cn

(编辑 刘锦伟)