基于高程多假设的地固单站短基线运动辐射源跟踪方法
张 敏,邓 伟,薄 超,晏行伟,郭福成
(1.国防科技大学电子信息系统复杂电磁环境效应国家重点实验室,湖南 长沙 410073;2.北京航天万源科技有限公司,北京 100176;3.中国航天科工集团8511研究所,江苏 南京 210007)
0 引言
自身不发射电磁信号,仅利用地面固定的单个或多个观测站被动接收和处理非合作运动辐射源的电磁信号,进而确定辐射源运动状态的无源跟踪滤波技术,在侦察监视、战略预警、战场态势感知、搜索救援等军用和民用领域具有重要应用价值[1-3]。

(1)

(2)
式中,矩阵R表示各坐标上加速度噪声的协方差阵。在以上状态矢量基础上建立观测模型为:
zk=fxk+vk
(3)
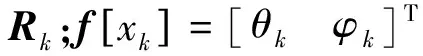
(4)

φk=2π/λ(r1k-2r2k+r3k)
(5)
式中,λ为信号波长,r1k=((pk-p1o)T(pk-p1o))1/2,r2k=((pk-p2o)T(pk-p2o))1/2,r3k=((pk-p3o)T(pk-p3o))1/2,p1o=[x1oy1oz1o]、p2o=[x2oy2oz2o]、p3o=[x3oy3oz3o]分别为三个阵元的位置。需要注意的是这里没有考虑三阵元等长短基线差分相位差的模糊,可通过多个接收天线解差分相位差模糊,解模糊的方法可参考文献[7]~[8]。
2 高程多假设方法
2.1 扩展卡尔曼滤波
对运动辐射源跟踪滤波中,应用最广泛的滤波算法是基于测量方程一阶泰勒级数展开的扩展卡尔曼滤波(EKF)方法,EKF定位方法的滤波方程[9]如下:EKF滤波方程如下:状态预测:
xk|k-1=Φk|k-1xk-1|k-1
(6)
预测误差协方差:

(7)
Kalman增益:
(8)
状态更新:
xk|k=xk|k-1+Kk[zm-Hkxk|k-1]
(9)
更新误差协方差:
(10)
式中,Hk为测量方程在预测点xk|k-1处计算的Jacobi矩阵。为了适应具有显著高程的运动辐射源,在扩展卡尔曼滤波的基础上,设计了一种基于高程多假设运动辐射源跟踪方法。

图1 基于高程划分的快速跟踪滤波原理
2.2 高程多假设滤波原理
本文设计的跟踪滤波方法通过多个滤波器组同时在不同高程进行跟踪滤波,最终通过加权计算的方式融合多个滤波器结果,在保证对目标跟踪定位精度的前提下,实现更为快速的跟踪定位。将辐射源可能的最大高程hmax划分为C个值,在每个高程值下对辐射源运动状态进行跟踪滤波处理。不失一般性,可将高程进行等间隔划分,取每个区间的中点作为对应的高程值。对应的高程多假设扩展卡尔曼滤波原理如图1所示。在上图所示的算法流程示意图中,每个滤波器可以采用扩展卡尔曼滤波(EKF)方法进行跟踪滤波计算。根据上述高程划分,对应的每个滤波器的初始状态和误差协方差为:
(11)Pk-1|k-1(c)=diag([Pp,Pv])
(12)
式中,c=1,…,C,C为高程划分的数量,Pp为一维测向+短基线差分相位差定位误差协方差,Pv为速度误差协方差,可取为Pv=diag([(vmax/2)2,(vmax/2)2]),vmax为辐射源可能的最大运动速率。
2.3 高程多假设滤波算法
当获得初始权值、均值和协方差后,通过递推滤波方法,进行跟踪滤波计算。状态预测:xk|k-1(c)=Φk|k-1xk-1|k-1(c)

(14)ωk|k-1(c)=ωk-1|k-1(c)
(15)
状态更新:
xk|k(c)=xk|k-1(c)+Kk(c)νk(c)

(18)
式中,新息为:
νk(c)=zk-f(xk|k-1(c))
(19)
新息协方差矩阵为:
(20)
Jacobi矩阵为:
Hk(c)=∂fk/∂xk|k-1(c)
(21)
卡尔曼增益为:
(22)
权值更新:

(23)
加权输出:
ωk|k(c)xk|k(c)
(24)
3 跟踪误差的理论性能
在不考虑系统噪声的情况下,基于多次观测跟踪滤波的克拉美-罗下限(CRLB)可通过EKF滤波的形式得到[1],所不同的就是Jacobi矩阵的计算使用的是目标位置的真值。利用运动辐射源运动状态真值,得到的滤波协方差为Pk-1|k-1的计算过程如下:
(25)
初始条件为:
(26)
其中,P0为有先验信息条件下的状态先验误差矩阵。因此观测时刻tk的定位误差的CRLB可定义为:

(27)
式中,trace(·)表示求矩阵的迹。
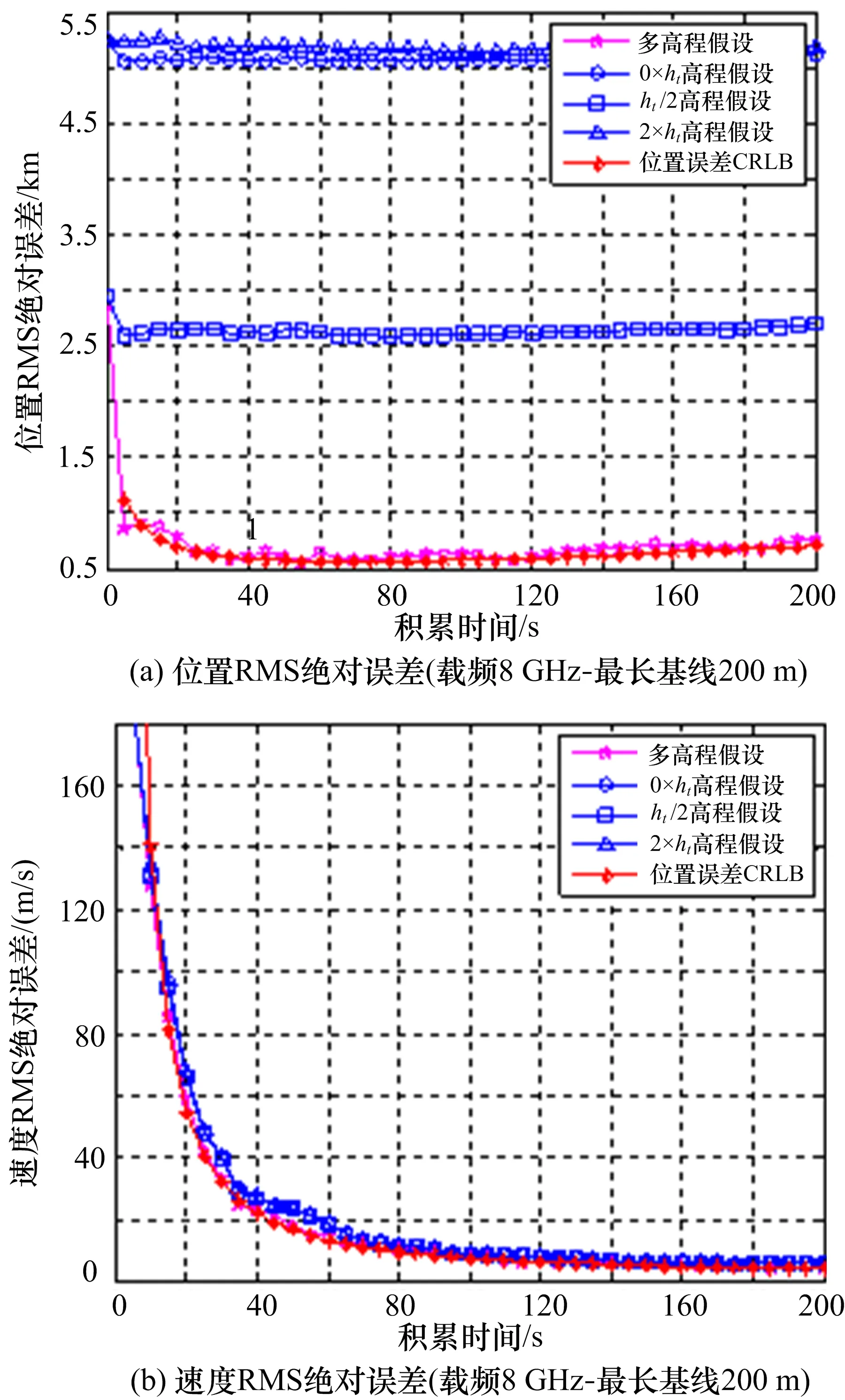
图2 辐射源初始距离50 km

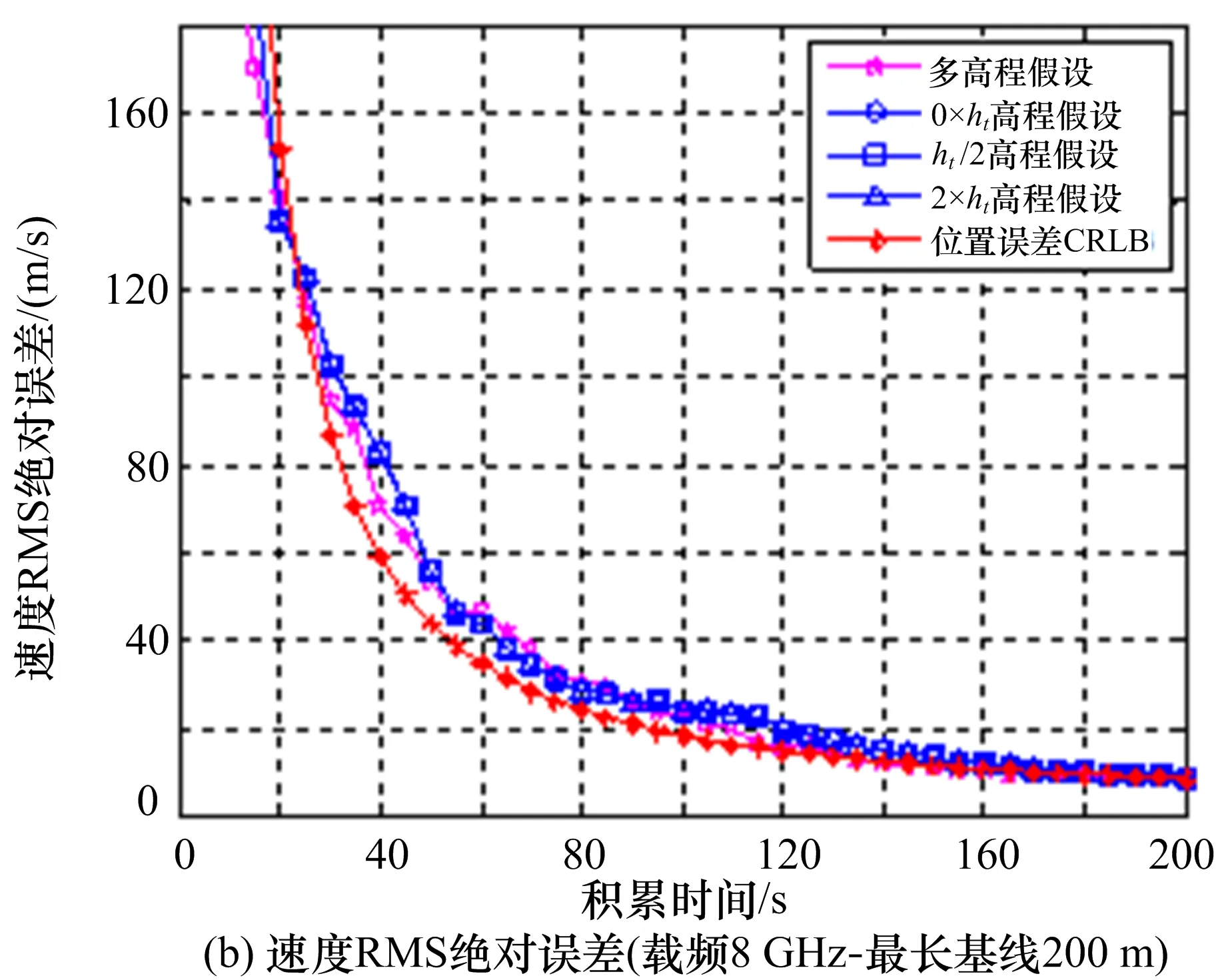
图3 辐射源初始距离100 km
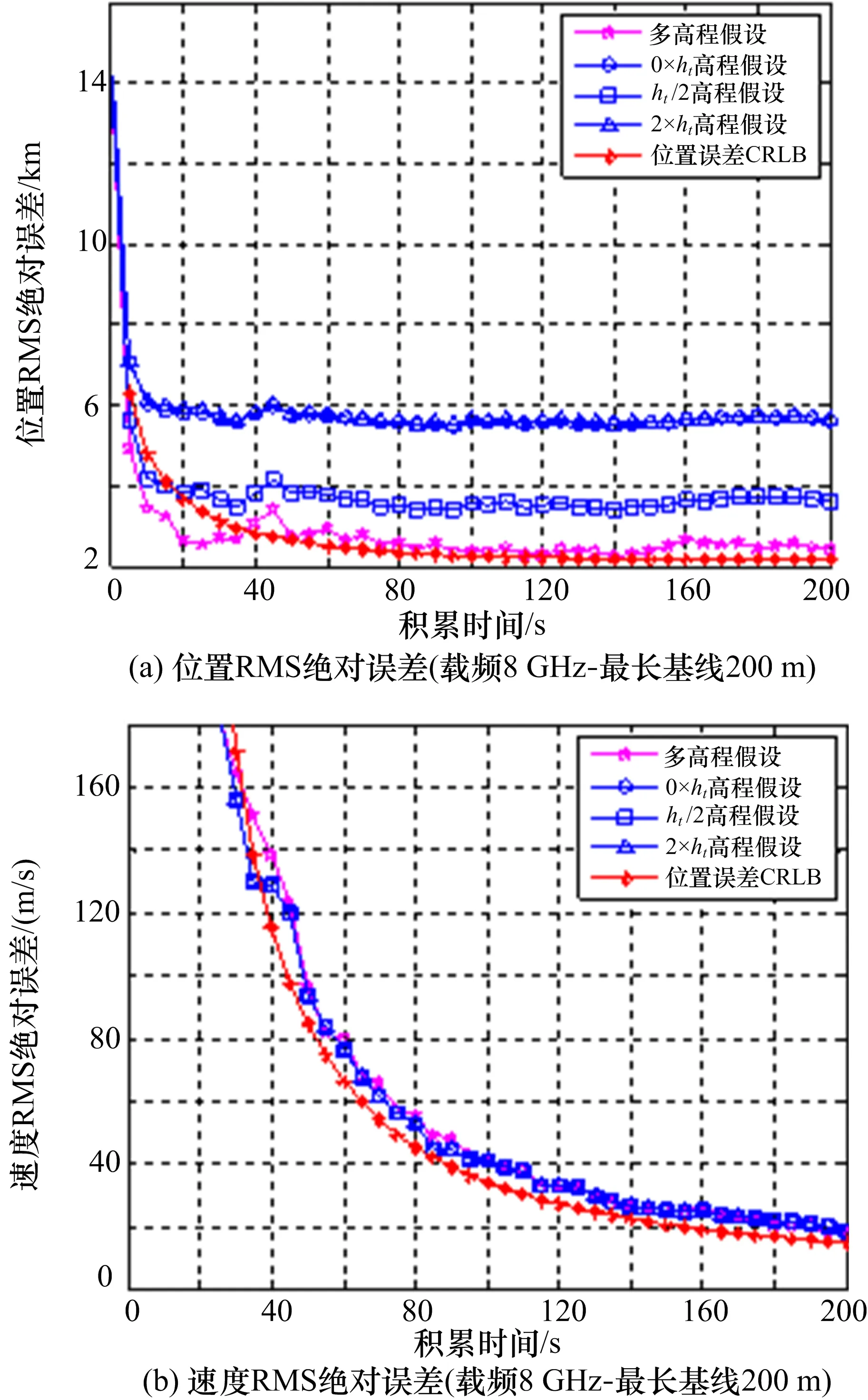
图4 辐射源初始距离150 km
4 仿真性能
为了验证提出算法的有效性,下面进行计算机仿真。典型仿真条件如下:假设观测站的位于定位坐标系原点,等间隔三阵元短基线最长基线长度为200 m;初始时刻辐射源到观测站的距离分别为50 km、100 km、150 km;初始时刻辐射源到观测站连线与真北方向的夹角为45°;辐射源的运动速度为300 m/s,飞行航向与真北方向的夹角为90°;辐射源载频分别为8 GHz;辐射源飞行高度为5 km;一维测向精度为1°;一维测向和差分相位差的数据率为2 Hz,即每秒钟测量2次时差和相位差。采用蒙特卡洛方法对运动辐射源位置和速度跟踪的均方误差(RMS)进行统计,仿真次数为50次。对不同辐射源初始距离下得到的仿真结果如图2~4所示。从仿真结果可以看到:1)当采用高程假设(零高程、半倍高程、2倍高程)进行跟踪滤波时,对辐射源位置RMS误差都会存在显著,且与真实高程差异越大,位置估计RMS误差越大;而在不同高程假设下对辐射源速度估计RMS误差基本相当。2)在不同辐射源初始距离下,初始距离越小高程假设引起的位置RMS误差越显著。3)采用本文多高程假设的跟踪滤波方法,在不同辐射源初始距离下,对辐射源位置和速度估计RMS误差都可接近CRLB,表明本文方法的有效性。
5 结束语
本文采用地面固定单站测一维测向+短基线差分相位差实现对运动辐射源跟踪滤波,当匀速巡航运动辐射源存在显著的高程时,采用传统的常规高程假设会造成显著的跟踪误差,本文提出的一种基于高程多假设的地固单站一维测向+短基线差分相位差的运动辐射源跟踪方法,采用多个并行的具有不同高程的扩展卡尔曼滤波器进行跟踪滤波,通过计算每个滤波器的权值,输出加权后的滤波结果。通过蒙特卡洛计算机仿真验证了本文方法在不同场景下对辐射源位置和速度估计RMS误差都可接近CRLB,表明了本文方法的有效性。■

