白令海峡及其邻近海域潮汐潮能数值模拟
李蔷 高郭平,2 安佰超 程灵巧,2
(1上海海洋大学海洋科学学院,上海201306;2上海海洋大学大洋渔业资源可持续利用省部共建教育部重点实验室,上海201306)
0 引言
白令海峡位于亚洲东北端西伯利亚和北美洲西北端阿拉斯加之间,长约60 km,宽约85 km,深约50 m,南与白令海相接,北与楚科奇海相连,是沟通太平洋与北冰洋的唯一航道。白令海是太平洋最北端的边缘海,东北部是水深小于200 m的宽广大陆架,存在阿纳德尔湾和诺顿湾两个海湾,以及圣劳伦斯岛、努尼瓦克岛和圣马休岛3个主要岛屿,经白令海峡延伸向楚科奇海。楚科奇海是北冰洋的边缘海,东至巴罗角,南至科策布湾,西至费兰格尔岛,平均水深约70 m(图1)。白令海峡及其邻近海域是太平洋与北冰洋之间海水交换的重要通道。
白令海峡的水交换对北冰洋的大气、海洋和海冰系统的显著变化有一定作用[1-4]。通过白令海峡北向输入的淡水通量占北冰洋淡水总量的40%[5],对北冰洋的温盐结构和生物地球化学结构有深刻影响[6],并通过弗拉姆海峡以及加拿大群岛间的水道进入北大西洋并对其产生影响[7]。白令海峡的水交换携带的碳、营养盐和浮游生物,对维持白令海–楚科奇海生态系统丰富的生产力有重要作用[8-10]。因此,研究白令海峡水交换的动力机制对北极研究具有重要意义。
风和潮汐是驱动海洋内部混合的主要机械能来源,大洋表层,风驱动海水混合,大陆架海区,潮汐为海洋的垂直混合提供能量[11]。潮汐是白令海峡区域的主要水动力环境控制因素之一,为该区域提供持续动力。潮汐在北冰洋混合过程中起着重要作用,会导致海冰的大量减少,对海水的温度、盐度和密度也有重要的影响作用。在海冰覆盖区,尤其是岸边固定冰覆盖地区,潮汐为海冰与海水之间的垂直混合提供主要动力[12-15]。Zhang等[16]对白令海海冰变化进行模拟,发现潮汐通过改变海冰的运动变形及海流影响海冰的空间分布。Luneva等[17]发现潮汐在北冰洋海冰减少因素中占15%,在减少上层海水(100 m内)的淡水及热量因素中占7%。
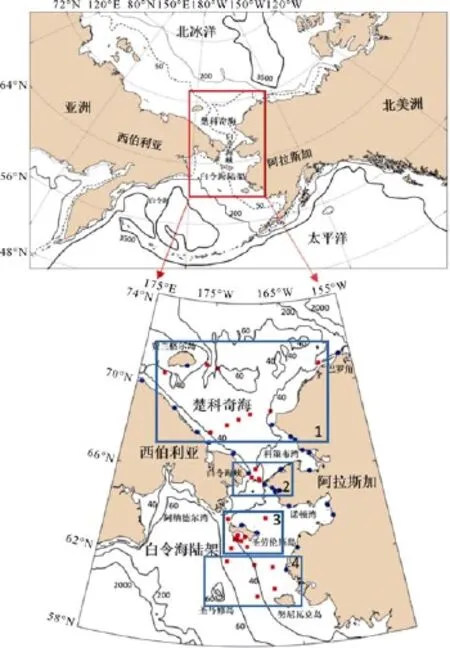
图1 研究区域水深地形及站位分布.蓝色圆点: 潮位站;红色正方形: 潮流站Fig.1.Topography of study area and distribution of observation stations.Blue dot: tide-gauge station; Red square: current station
目前,数值模型是研究极地海洋的主要工具之一,然而北冰洋模型与观测分析论坛(FAMOS)中仅有少数全球和泛北极模型有足够的分辨率模拟陆架海中的物理海洋过程,其中包括 FVCOM(Finite-Volume Coastal Ocean Model)模型,分辨率达 1—50 km[18]; 全球 1/12° NEMO(Nucleus for European Modelling of the Ocean)模型[19-20];HYCOM 模型,分辨率达 3—5 km[21]。这些模型中,仅有 FVCOM真正解决了潮汐与复杂的地形岸线问题[17]。前人利用实测数据和模型分别对白令海和楚科奇海潮汐进行了大量研究[22-27],通常把白令海峡关闭,单独研究分析白令海和楚科奇海潮汐特征,并且少有人研究该海域的潮能通量和耗散。因此,本文基于有限体积海岸海洋模型FVCOM,把白令海陆坡、白令海峡以及楚科奇海陆坡作为一个整体,进行了高分辨率的潮汐数值模拟研究,利用实测潮汐潮流资料对模拟结果进行了验证,模拟结果和实测数据符合良好,说明了模拟结果的可靠性。在此基础上,分析了该海域潮汐潮流的分布及特征,研究其潮汐能的传播与耗散特性。
1 模式简介及应用
白令海峡及其邻近海域海岸线及海底地形复杂,区域内岛屿较多(图1),采用非结构型三角网格的海洋模式可以实现对分辨率及计算效率的要求,因此选取目前广泛应用的 FVCOM海洋数值模型,由美国麻省理工大学开发的新一代非结构全球海洋模式。基于海洋原始方程的三维海洋数值模型,水平方向采用非结构三角元有限体积算法,垂直方向采用σ坐标系来体现不规则的底部边界,模式的水平方向采用无结构化的三角形网格,空间分辨率灵活,较好拟合复杂的岸线。垂向混合系数由二阶湍流闭合模型(Mellor-Yamada模型)确定,水平扩散项由 Smagorinsky公式求得[28-30]。采用内、外模时间分裂法,内模时间步长较短,外模时间步长较长,节省运行时间。
本文计算的区域 175°E—155°W,58°N—75°N(图2)包括白令海陆架区,白令海峡,楚科奇海,由位于楚科奇海和白令海陆架上的两条开边界闭合而成。该海域岸线复杂,包含许多岛屿,众多海湾,因此选用非结构三角网格模式能够在适当的计算需求下,实现该海域的高分辨率模拟。在水平方向上,利用 SMS(Surface-Water Model System)软件生成了高质量、无结构化的不规则三角形网格,通过改变分辨率的方法,实现了在海峡及岛屿区域对网格的加密,在白令海峡分辨率最高为1 km,在开边界处分辨率最低为10 km,整个计算区域共包括54 534个网格节点和106 187个三角单元。垂直方向分为 10个等间隔的σ层,模式设置内模步长为30 s,外模步长为3 s。
图2 模式计算区域网格Fig.2.Mesh structure of computational domain in the used model
水深资料和岸线资料对潮汐潮流的数值模拟的准确性至关重要,水深资料来自 NOAA(National Oceanic and Atmospheric Administration)数据中心的 GEBCO格点化水深数据,分辨率为30'×30',通过内插求得其余海域各计算网格点的水深,在岸边区域模型最小水深设为5 m,得到较精确的海区水深数据; 岸线数据利用 GEODASNG软件,从 NOAA数据中心发布的 GSHHG(Global Self-consistent,Hierarchical,High-resolution Geography Database)中提取白令海峡海域的高精度岸线数据。
FVCOM模式的驱动力包括潮汐、风、大气压、热通量、降水与蒸发、河淡水通量以及海冰,本文仅分析潮汐结果。潮汐模式由 8个天文分潮K1、O1、Q1、P1、M2、K2、N2和S2产生的平衡潮驱动,本文将来自全球海洋潮汐模型(TPXO7.2)中研究海域的上述 8个分潮的调和常数,利用OTPS(Osu Tidal Prediction Software)差值到模式的开边界点上,再利用以下水位预报公式进行计算:
其中,ζ为水位,hi、gi和wi分别是第i个分潮的振幅、迟角和角速度,fi为分潮的交点因子,ui为分潮的焦点订正角,voi为分潮的天文初位相位。计算开边界节点处在5月1日—7月31日(UTC),共计92 d的水位时间序列,作为开边界的驱动。在正压模式中,整个海洋初始是静止的,不考虑风、大气压力、热通量、淡水通量的影响,也不考虑分层的影响。模式区域内的所有三角网格中心的水平垂向速度均为 0,不考虑温度和盐度的变化,分别取常数,参考前人工作基础[25],底摩擦系数取0.002 5。模式模拟5月1日—7月31日计算区域的潮汐和潮流状况,每 1小时输出一次结果,待模型稳定后,取运行30 d后的模拟结果进行调和分析。
2 模型验证
为验证模型模拟结果的准确性,收集到26个潮位站和 28个海流的锚系数据资料(图1),来自于 3个数据中心: NOAA潮汐潮流中心(http://tidesandcurrents.noaa.gov/)、阿拉斯加大学(http://www.ims.uaf.edu/tide/)和华盛顿大学极地科学中心(http://psc.apl.uw.edu/)。潮位站和海流的锚系数据均满足 Lefèvre等[31]提出的有关验潮资料的标准: 验潮站位置具有连贯性,数据资料连续且时间超过1个月。从图1可以看出,潮位站多位于美国阿拉斯加和圣劳伦斯岛沿岸地区,其调和常数来自NOAA潮汐潮流中心,其结果都是基于一年以上的观测值,足够准确; 俄罗斯西伯利亚沿岸仅有6个,且均位于楚科奇海,其调和常数来自阿拉斯加大学 Kowalik和 Proshutinsky[32-33]对北极潮汐的观测。海流的锚系数据在白令海峡、白令海陆架和楚科奇海均有分布,均来自华盛顿大学极地科学中心。本节分别利用以上实测潮位站、海流的锚系数据对模型模拟的潮汐、潮流结果进行验证。
2.1 潮汐验证
因为研究海域振幅普遍较小,会影响迟角的方差,导致迟角不稳定,仅仅比较潮汐调和常数的观测值与模拟值的均方根是不合理的,因此,除对比均方根之外,还对比了相对差值D,公式如下:
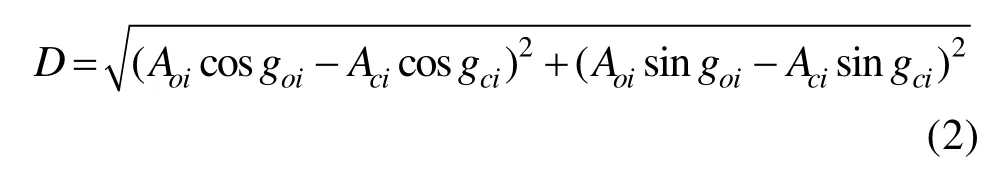
其中,Aoi和goi分别是第i个站点振幅和迟角的观测值,Aci和gci分别是与观测值对应的模拟值。所有振幅的均方根误差公式如下:
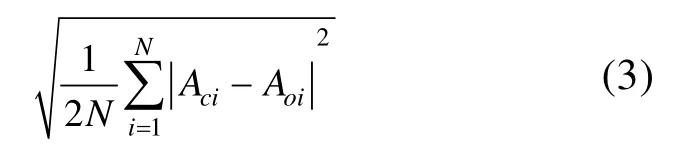
利用收集的验潮站调和常数,与模型模拟结果进行对比。在本文计算区域内,选取了26个验潮站的实测资料,通过插值寻找与观测点距离最近的点,对比 M2、K1分潮观测站与其对应模拟值的结果(表1)。
整体上,实测验潮站调和常数与模拟结果吻合良好,M2分潮的振幅、迟角的平均绝对误差为0.89 cm和10.95°,K1分潮的振幅、迟角的平均绝对误差为0.77 cm和7.34°,M2和K1分潮所有振幅的均方根误差分别为 3.26、2.95 cm(表1)。然而,从表1中可以看出,M2和K1的振幅、迟角的相对误差存在一些较大值,这些潮位站均位于诺顿湾、科策布湾等湾内沿岸。造成这种现象的原因可能有,潮汐模拟结果的准确性与水深精确度有关,模式采用的水深数据分辨率不足以精确刻画沿岸浅水区域,此外,进行对比时,通过插值和寻找距离观测点最近的模拟点并不能完全与实测站点重合。
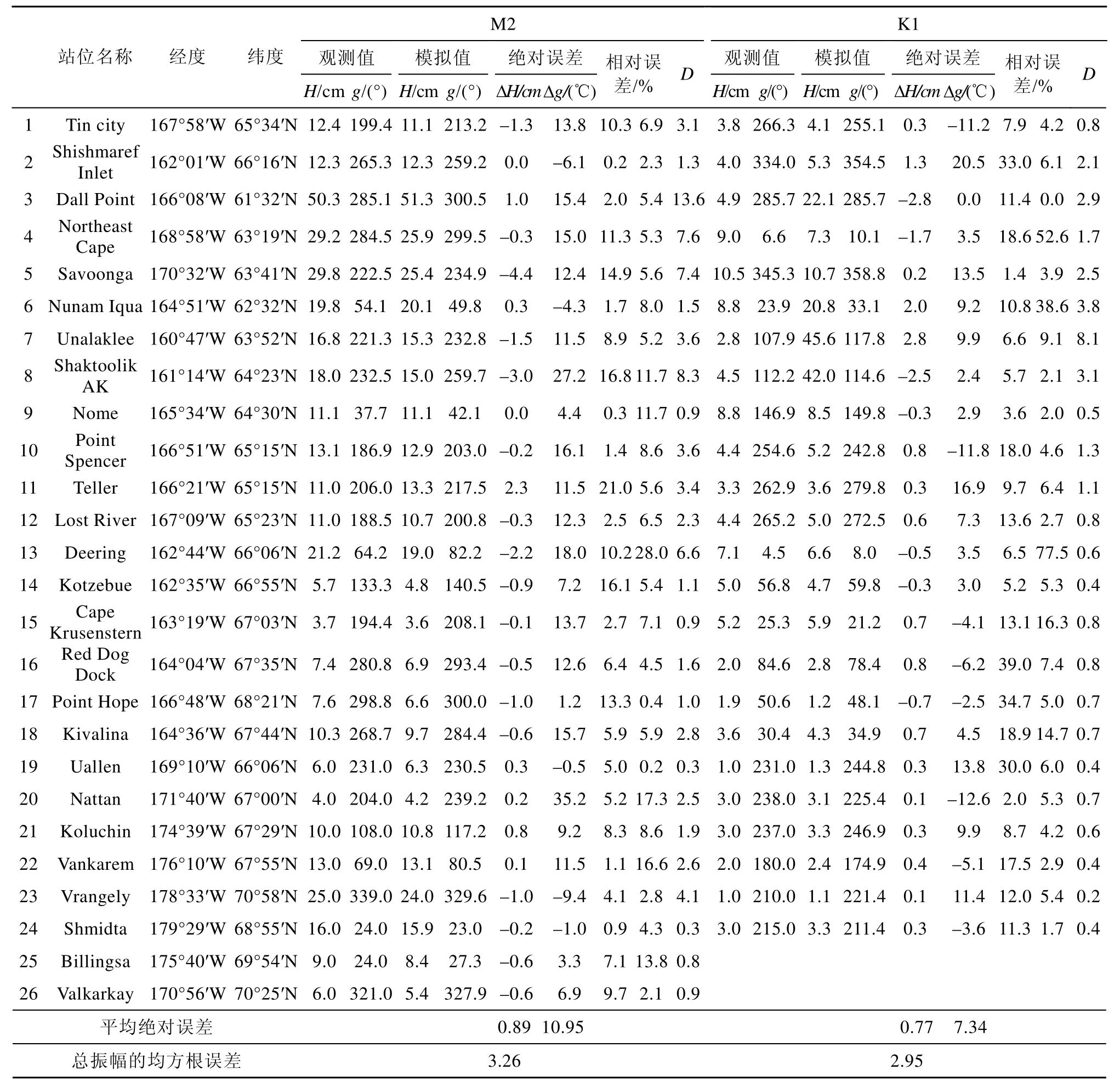
表1 M2、K1分潮调和常数实测值与模拟值对比Table 1.Observed and calculated tidal harmonic constant of M2,K1
2.2 潮流验证
利用收集的 28个海流锚系站的数据验证潮流模拟结果,根据其位置分布不同,划分为 4个区域(图1)。海流锚系数据来自声学多普勒海流仪(ADCP)和安德拉海流仪(RCM),数据进行线性差值和校准。根据实测数据水深,验证模拟结果相对应的σ层,其中ADCP实测数据用其测量深度的平均值,RCM 实测数据用测量深度。通过Matlab的调和分析工具(T-tide)对实测及模拟结果进行调和分析得到潮流椭圆要素。在验证潮流椭圆要素时面临两个问题: 一是潮流椭圆要素中的方向和相位会随季节和年份的变化而改变,即同一个站位的同一个深度上,不同时间记录的方向和相位会有差距; 二是实测站位的水深与模型使用的水深数据并不完全一致。Murty等[34]提出由于海冰覆盖的时空变化以及海水分层的季节和年际变化,潮流椭圆要素也有季节变化。本文仅在正压条件下模拟潮汐,因此,对待潮流验证结果应谨慎分析。
图3表明,整体上,各观测站点与模拟的潮流椭圆要素间的吻合性较高。在楚科奇海域及圣劳伦斯岛附近,实测与模拟潮流椭圆的长短半轴基本一致,方向略有偏差; 在白令海峡及努尼瓦克岛,模拟潮流椭圆的长短半轴均比实测小,方向也有差别。造成这种现象的原因除上述客观存在的问题,还有可能因为计算潮流只是三角形网格中心的流速,通过插值得到观测点上的流速,与实测站位并不能完全重合。潮流椭圆的验证结果表明,模拟结果能基本反映研究海域潮流的变化特征。
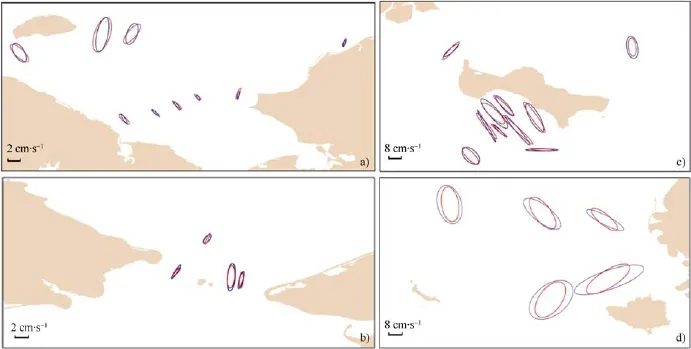
图3 M2底层潮流椭圆对比图.红色: 模式数据; 蓝色: 观测数据Fig.3.Comparison of the modeled and observed bottom M2 tide ellipse.Red ellipse: modeled results; blue ellipse: observed results
3 潮汐模拟结果分析
鉴于以上模拟结果的验证,模拟结果与实测情况符合较好,本节对模拟结果后60 d结果进行调和分析,得到M2、K1、N2、S2、O1五个主要分潮等振幅线、等迟角线和潮流椭圆要素,分析讨论研究区域潮汐、潮流的基本特征。
3.1 M2分潮
对每个网格点的模拟结果进行调和分析,计算得到M2分潮的潮汐调和常数和潮流椭圆参数,绘制 M2分潮的同潮图和潮流椭圆图(图4)。M2分潮同潮图(图4a)的分布状况与 Kowalik等[27,35]和Li[25]研究结果相似。研究海域M2分潮的振幅范围在2—100 cm。从图4a中可以看出,白令海陆架大部分海域振幅在30 cm以上。较大振幅出现在白令海陆架东南部,振幅值超过70 cm。在狭窄的浅海湾振幅增加,在诺顿湾振幅达到35 cm,阿纳德尔湾振幅可达60 cm。较小振幅出现在阿纳德尔湾的纳瓦林角、圣劳伦斯岛东南部、诺顿湾和白令海峡东南部,都形成旋转潮波系统。此外,楚科奇海整体振幅偏小,大部分海域振幅小于20 cm。较大振幅位于西伯利亚沿岸浅水区,振幅超过 30 cm。较小振幅位于科策布湾入口和波因特莱近岸处,在这两处存在旋转潮波系统。
从图4a中的等迟角线可以看出,来自白令海的半日潮波在进入白令海陆架时,受到半封闭地形的影响,部分潮波发生反射,在白令海陆架中形成多个逆时针旋转潮波系统。来自白令海的半日潮波通过白令海峡进入楚科奇海,与来自北冰洋向南传播的半日潮波相互干涉,在楚克奇海的科策布湾入口和波因特莱近岸处形成两个逆时针旋转潮波系统。
为更好了解研究海域的潮流的运动形式,图4b、c给出了M2分潮表层潮流椭圆分布,红色椭圆代表顺时针旋转潮流,蓝色椭圆代表逆时针旋转。研究海域潮流椭圆以逆时针旋转为主,然而,在沿岸地区出现顺时针旋转。从潮流椭圆的主轴长短可以看出,潮流在白令海东南部最强,由南向北逐渐减弱,在白令海峡处流速达到最小; 潮流在楚克奇海较弱,由南向北逐渐增强,在费兰格尔岛处较强。与图4a对比可以看出,强潮流与高振幅是相对应的,高振幅的地区潮流较强,低振幅的地区潮流较弱。
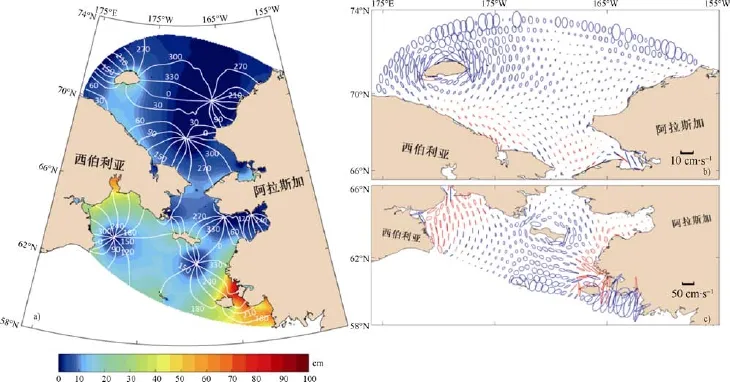
图4 M2分潮同潮图和潮流椭圆分布.a)同潮图(颜色填充: 潮汐振幅,单位为cm; 白色实线: 等迟角线格林尼治0:00);b),c)表层1 m潮流椭圆(红色: 顺时针旋转潮流; 蓝色: 逆时针旋转潮流)Fig.4.Cotidal charts and tidal ellipses of the M2 tide.a) cotidal chart(filled contours denote the magnitude of the tidal elevation amplitude(in centimeters),white contour lines denote the co-phase lags lines GMT at 0:00); b),c)tidal current ellipses are the surface ellipses at 1 m depth(red ellipses denote clockwise rotation; blue ellipses denote counterclockwise rotation)
3.2 K1分潮
通过每个网格点调和分析得到 K1分潮潮汐调和常数和潮流椭圆参数,绘制K1分潮的同潮图和潮流椭圆图(图5)。从K1分潮同潮图(图5a)可以看出,K1分潮的潮汐结构比M2分潮简单。研究海域K1分潮的振幅范围在2—70 cm,最大振幅出现在白令海陆架东南沿岸和诺顿湾里,这与 Kowalik[35]的研究结果一致。整体趋势从白令海向楚科奇海递减,楚克奇海潮汐微弱,振幅均在6 cm以下。从图5a中的等迟角线可以看出,来自白令海的全日潮波进入白令海陆架后向东北传播,经过圣劳伦斯岛进入诺顿湾,在诺顿湾以全日分潮为主。潮波继续向北传播,通过白令海峡进入楚克奇海,与北冰洋的潮波相互作用,在楚科奇海形成旋转潮波系统。
图5b、c给出了K1分潮的潮流椭圆图,从图中可以看出,楚科奇海潮流流速普遍很小,白令海潮流流速比楚科奇海流速大,较大流速位于白令海阿拉斯加沿岸,最大流速出现在诺顿湾。与M2分潮潮流不同的是,K1在阿拉斯加沿岸潮流均为顺时针旋转,在阿纳德尔湾顺时针旋转潮流较少。在诺顿湾里 K1分潮潮流比 M2分潮潮流强,这也证明在诺顿湾,K1分潮占主导地位。
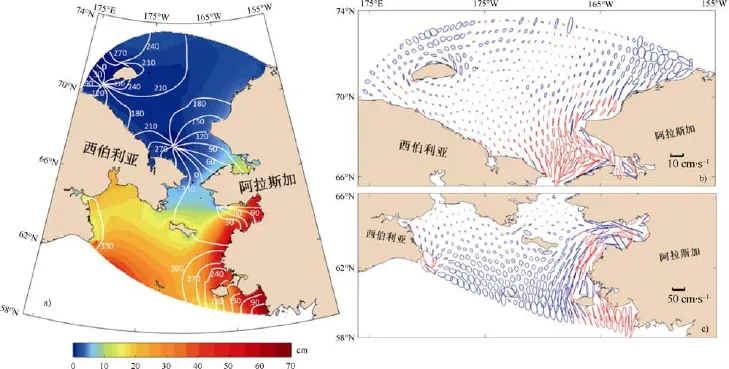
图5 K1分潮同潮图和潮流椭圆分布.a)同潮图(颜色填充: 潮汐振幅,单位为cm; 白色实线: 等迟角线格林尼治0:00);b),c)表层1 m潮流椭圆(红色: 顺时针旋转潮流; 蓝色: 逆时针旋转潮流)Fig.5.Cotidal charts and tidal ellipses of the K1 tide.a) cotidal chart(filled contours denote the magnitude of the tidal elevation amplitude(in centimeters),white contour lines denote the co-phase lags lines GMT at 0:00); b),c)tidal current ellipses are the surface ellipses at 1 m depth(red ellipses denote clockwise rotation; blue ellipses denote counterclockwise rotation)
3.3 N2、S2和O1分潮
研究海域的潮汐主要受北太平洋向北传入白令海的潮波影响,其次受北冰洋向南传播的潮波影响。白令海陆架4个主要分潮分别是M2、N2、K1和O1,楚克奇海4个主要分潮分别是M2、S2、K1和O1。N2、S2和O1也是研究海域的主要分潮,调和分析得到 3个分潮的调和常数。限于篇幅,N2、S2和O1的同潮图和潮流椭圆没有给出。N2和S2分潮的潮汐系统特征与M2分潮相似,在研究海域存在6个无潮点,振幅比M2分潮小,但是在白令海陆架上,N2分潮的振幅比 S2分潮的振幅大,在楚克奇海S2分潮振幅比N2分潮振幅大。O1分潮的潮汐系统特征与K1分潮相似,在楚克奇海存在1个无潮点,振幅比K1分潮的振幅小。
4 潮汐能通量和耗散
潮汐是驱动海洋内部混合的主要机械能来源[11],在浅海中湍底边界层(bottom boundary layer,BBL)主导耗散平衡。白令海峡及其邻近海域的潮汐能通量及耗散并未很好估算,本节计算研究海域的潮能通量和潮能 BBL耗散,对其潮汐动力进行分析。
4.1 潮能通量传播
潮能通量的计算公式如下:
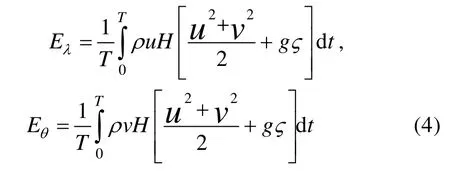
式中,Eλ和Eθ分别代表潮能通量在纬向和经向的分量,u和v分别代表潮流速度在纬向和经向的分量,H代表水深,ς代表潮位,ρ是海水密度,是重力加速度,T是潮周期。M2(图6a)和 S2、N2(未给出)潮能的空间分布相似,但S2和N2分潮潮汐能大小仅为 M2分潮的 1/10,并且在楚克奇海S2比N2潮能通量大,在白令海陆架N2比S2潮能通量大。K1(图6b)和 O1(未给出)潮能的空间分布也相似,但是O1比K1潮能通量小。为了研究半日分潮和全日分潮潮能通量的不同,分别以M2和K1分潮为代表,绘制M2和K1分潮的潮能通量矢量分布图。
利用正压半日潮潮能的传播途径研究 M2分潮潮能传播的空间分布(图6)。研究海域主要受到太平洋向北传入白令海的潮能影响,其次受到北冰洋向南传入楚科奇海的潮能影响。研究海域水深较浅,潮流速度较小,潮能通量较小,潮能从白令海传入白令海陆架,分成两部分,一部分向西北传播,在阿纳德尔海峡又分为两支,一支继续向西北传播进入阿纳德尔湾,并在阿纳德尔湾沿岸反射,形成一个逆时针传播,另一支在阿纳德尔海峡处向东北传播,并在圣劳伦斯岛沿岸形成顺时针传播; 另一部分向东北传播,穿过斯番博格海峡进入诺顿湾。来自白令海的潮能继续向北传播,通过白令海峡,进入楚科奇海。来自北冰洋的潮能向南进入楚克奇海,也分为两部分,一部分从西伯利亚沿岸向南传播至白令海峡,另一部分沿费兰格尔岛形成顺时针传播。
研究海域中的K1分潮潮能传播特征与M2分潮潮能传播特征有很多区别。从图6b可以看出,K1分潮潮能从白令海传入白令海陆架分为两部分。一部分沿着阿纳德尔湾向北传播,在阿纳德尔湾入口处分为三支。第一支向北进入阿纳德尔湾里,并在阿纳德尔湾沿岸发生反射形成逆时针传播,但相对于M2潮汐能小得多,且范围仅局限在阿纳德尔湾里。第二支一直向东北传播,遇到圣劳伦斯岛分为南北两支,北面一支的小部分继续向北穿过白令海峡传入楚克奇海,其余部分向东传入诺顿湾,南面一支沿圣劳伦斯岛南岸穿过斯番博格海峡进入诺顿湾。第三支在阿纳德尔湾入口处向东南传播,在圣马休岛与奴尼瓦克岛之间发生偏折后向东北传播,最终传入诺顿湾。另一部分沿阿拉斯加沿岸向西北传播,至奴尼瓦克岛继续向北传播。
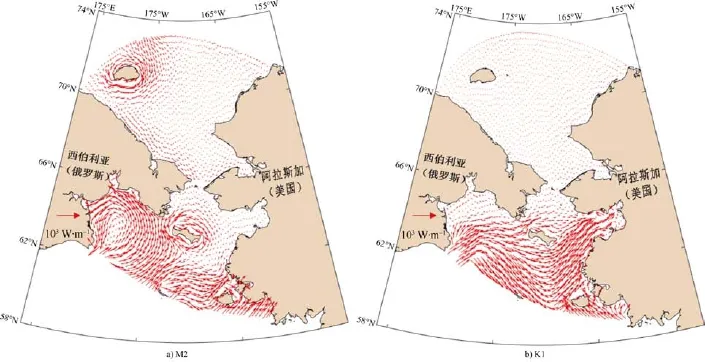
图6 M2和K1分潮的潮能通量矢量分布(单位: W·m–1)Fig.6.Distribution of the M2,K1 tidal energy flux(Unit: W·m–1)
4.2 不同断面的潮能通量
为了初步研究潮汐能的空间分布特征,在研究海域选取了7条断面(图7),计算讨论了通过不同断面的潮汐能通量,其中 A、B断面为白令海进入白令海陆架截面,C、D断面为北冰洋进入楚科奇海截面,L1为阿纳德尔海峡截面,L2为斯番博格海峡截面,L3为白令海峡截面。
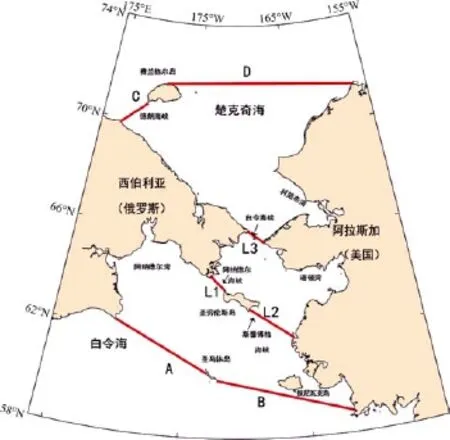
图7 计算断面分布Fig.7.Distribution of sections
表2为4个主要分潮在各个截面上的潮能通量值,M2、S2、K1、O1四个主要分潮通过A、B、C、D断面进入研究海域的潮能通量分别为384.945、6.554、285.321和 73.707 MW(1 MW=106W),其中M2分潮约占4个分潮总入射能的51%,K1分潮约占38%,O1分潮约占10%。
在诺顿湾海域,潮能耗散总量约为188 MW,其中 K1分潮潮能耗散约 131 MW,约占总量的70%; 在圣劳伦斯岛以南的白令海陆架区,潮能耗散总量约为526 MW,其中M2分潮潮能耗散约369 MW,约占总量的70%。潮能进入白令海陆架后,M2分潮主要在圣劳伦斯岛以南陆架区耗散,K1分潮主要在诺顿湾海区耗散。从通过C、D两个截面的潮能通量可以看出,经过C断面的半日分潮潮能为正,全日分潮潮能为负,即半日分潮潮能通过德朗海峡进入楚克奇海,全日分潮潮能通过德朗海峡流出楚克奇海; D断面与C断面情况相反。
4.3 潮能BBL耗散
计算4个主要分潮的底边界耗散。底边界潮能耗散公式由Taylor于1919年提出:
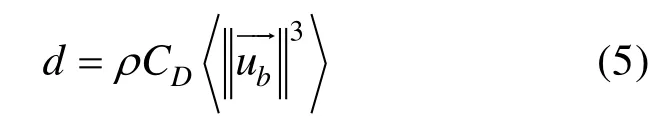
对d在整个海域进行积分,就得到整个海域的潮能耗散:
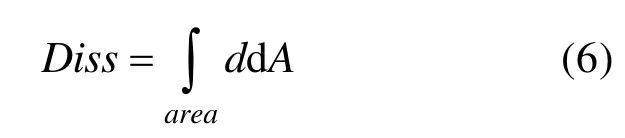
式中,CD为底摩擦系数,取0.002 5,ρ为海水密度,为底层速度,括号代表在一个潮周期内进行平均,A是三角单元的面积。
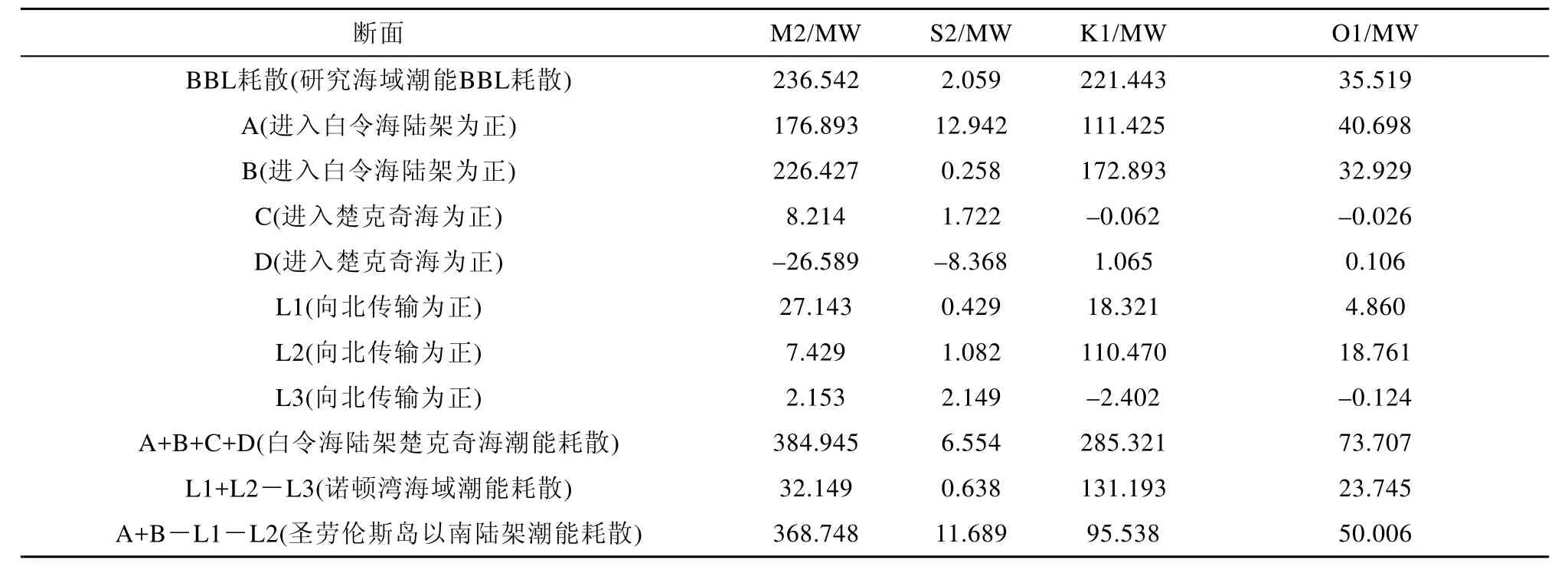
表2 计算各断面的潮能通量Table 2.Tidal energy fluxes across different sections(1 MW=106 W)
图8是M2、S2、K1和O1四个主要分潮的底边界耗散,等值线代表潮能耗散取对数后的值。从图中可以看出,M2分潮和S2分潮的底摩擦耗散相似,K1分潮和O1分潮的底摩擦耗散相似,分别与图4中的M2、K1分潮的潮流椭圆分布特征接近。在楚克奇海M2分潮的耗散比S2分潮的耗散大1—2个量级,在白令海陆架M2分潮的耗散比 S2分潮的耗散大得多。在白令海陆架K1分潮的耗散比O1分潮的耗散大1—2个量级,在楚克奇海K1和O1分潮的耗散都很小。
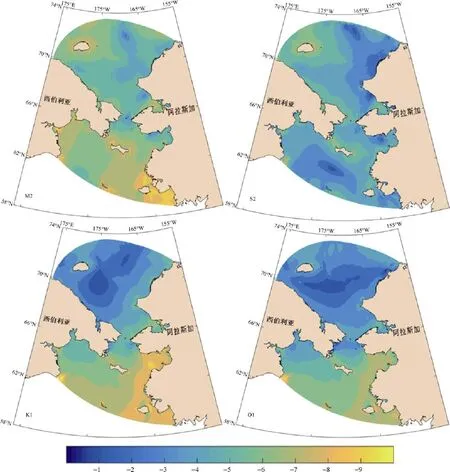
图8 4个主要分潮底边界耗散分布:lgd(d的单位:W·m–2)Fig.8.Distributions of the BBL of M2,S2,K1 and O1 constituents: lgd(unit of d: W·m–2)
从表2中可以看出,四个主要分潮M2、S2、K1和O1在研究海域的底边界层(BBL)的耗散值分别为 236.542、2.059、221.443和35.519 MW,分别约占研究海域内总耗散的61%、31%、78% 和48%。四个主要分潮的总BBL耗散为495.563 MW,约占总耗散量的 66%,相应地,约 34%的潮能参与到海水的内部混合过程中,其中,四个主要分潮M2、S2、K1和O1分别约有148.403、4.495、63.878和38.188 MW潮能进行了内部混合。
5 结论与讨论
本文基于FVCOM海洋数值模型对白令海峡及其邻近海域的潮汐、潮流进行数值模拟研究,模拟结果与实测吻合良好,能够较真实地反映研究海域正压潮潮汐及潮汐能的特征。
研究结果如下。
1.研究海域潮汐主要受白令海的潮汐影响,其次受到北冰洋微弱的潮汐影响。白令海陆架4个主要分潮分别是M2、N2、K1和O1,楚克奇海4个主要分潮分别是 M2、S2、K1和 O1。潮汐类型混合复杂,白令海陆架区以半日潮为主,但在诺顿湾海域附近以全日潮为主,楚科奇海和白令海峡主要以半日潮为主。研究海域M2分潮存在6个无潮点,K1分潮也存在1个无潮点。造成这种现象的原因主要是半日潮与全日潮的相互作用以及阿拉斯加、西伯利亚沿岸独特的地形和水深。
2.研究海域潮流椭圆以逆时针旋转为主,沿岸地区存在一些顺时针旋转。M2分潮潮流在白令海陆架东南部及阿纳德尔湾较强,K1分潮潮流在诺顿湾潮流达到最大值。重力、科氏力和水深分布在潮汐动力过程中发挥着重要作用。
3.研究海域潮能通量较小,这是由于水深较浅,潮流速度也较小,4个主要分潮在白令海陆架和楚科奇海的潮能耗散总量约为 751 MW(1 MW=106W),M2潮能耗散占总量的52%,K1潮能耗散占总量的38%; 在诺顿湾海域,潮能耗散总量约为188 MW,K1潮能耗散占总量的70%;在圣劳伦斯岛以南的白令海陆架区,潮能耗散总量约为526 MW,M2潮能耗散占总量的70%。潮能进入白令海陆架后,M2分潮主要在圣劳伦斯岛以南陆架区耗散,K1分潮主要在诺顿湾海区耗散。
此外,本文仅研究正压条件下的潮汐潮能特征,未考虑其他条件,然而在楚科奇海海域,夏季仍存在浮冰和固定冰,海冰对潮汐振幅的影响不大,但其对潮汐迟角和潮流椭圆方向有较大影响,造成楚科奇海海域潮汐迟角和潮流椭圆方向的误差。在今后的工作中,以此潮汐动力背景为基础,进一步考虑海冰等的影响。
1 陈立奇,赵进平,卞林根,等.影响北极地区迅速变化的一些关键过程研究[J].极地研究,2003,15(4): 283—302.
2 Cooper L W,Whitledge T E,Grebmeier J M,et al.The nutrient,salinity,and stable oxygen isotope composition of Bering and Chukchi Seas waters in and near the Bering Strait[J].Journal of Geophysical Research: Oceans(1978—2012),1997,102(C6): 12563—12573.
3 Hu A X,Meehl G A,Han W Q.Role of the Bering Strait in the thermohaline circulation and abrupt climate change[J].Geophysical Research Letters,2007,34(5): L05704.
4 高郭平,赵进平,董兆乾,等.白令海峡海域夏季温、盐分布及变化[J].极地研究,2004,16(3): 229—239.
5 Woodgate R A,Aagaard K.Revising the Bering Strait freshwater flux into the Arctic Ocean[J].Geophysical Research Letters,2005,32(2): L02602.
6 Carmack E C,Macdonald R W,Perkin R G,et al.Evidence for warming of Atlantic water in the southern Canadian Basin of the Arctic Ocean: results from the Larsen-93 expedition[J].Geophysical Research Letters,1995,22(9): 1061—1064.
7 Steele M,Morison J,Ermold W,et al.Circulation of summer Pacific halocline water in the Arctic Ocean[J].Journal of Geophysical Research: Oceans(1978—2012),2004,109(C2): C02027.
8 Grebmeier J M,McRoy C P,Feder H M.Pelagic-benthic coupling on the shelf of the northern Bering and Chukchi seas.1.Food supply source and benthic biomass[J].Marine Ecology-Progress Series,1988,48: 57—67.
9 Walsh J J,McRoy C P,Coachman L K,et al.Carbon and nitrogen cycling within the Bering/Chukchi Seas: source regions for organic matter effecting AOU demands of the Arctic Ocean[J].Progress in Oceanography,1989,22(4): 277—359.
10 Springer A M,McRoy C P.The paradox of pelagic food webs in the northern Bering Sea—III.Patterns of primary production[J].Continental Shelf Research,1993,13(5—6): 575—599.
11 Munk W,Wunsch C.Abyssal recipes II: energetics of tidal and wind mixing[J].Deep Sea Research Part I: Oceanographic Research Papers,1998,45(12): 1977—2010.
12 Padman L,Dillon T M.Turbulent mixing near the Yermak Plateau during the coordinated Eastern Arctic Experiment[J].Journal of Geophysical Research: Oceans,1991,96(C3): 4769—4782.
13 Wang J,Kwok R,Saucier F J,et al.Working toward improved small-scale sea ice-ocean modeling in the Arctic seas[J].EOS,Transactions American Geophysical Union,2003,84(34): 325—330.
14 Holloway G,Proshutinsky A.Role of tides in Arctic ocean/ice climate[J].Journal of Geophysical Research: Oceans,2007,112(C4):C04S06.
15 St.Laurent L,Garrett C.The role of internal tides in mixing the deep ocean[J].Journal of Physical Oceanography,2002,32(10):2882—2899.
16 Zhang J L,Woodgate R,Moritz R.Sea ice response to atmospheric and oceanic forcing in the Bering Sea[J].Journal of Physical Oceanography,2010,40(8): 1729—1747.
17 Luneva M V,Aksenov Y,Harle J D,et al.The effects of tides on the water mass mixing and sea ice in the Arctic Ocean[J].Journal of Geophysical Research: Oceans,2015,120(10): 6669—6699.
18 Chen C S,Gao G P,Qi J H,et al.A new high-resolution unstructured grid finite volume Arctic Ocean model(AO-FVCOM): an application for tidal studies[J].Journal of Geophysical Research: Oceans(1978—2012),2009,114(C8): C08017.
19 Bacon S,Marshall A,Holliday N P,et al.Seasonal variability of the east Greenland coastal current[J].Journal of Geophysical Research:Oceans,2014,119(6): 3967—3987.
20 Duchez A,Frajka-Williams E,Castro N,et al.Seasonal to interannual variability in density around the Canary Islands and their influence on the Atlantic meridional overturning circulation at 26°N[J].Journal of Geophysical Research: Oceans,2014,119(3):1843—1860.
21 Metzger E J,Smedstad O M,Thoppil P G,et al.US Navy operational global ocean and Arctic ice prediction systems[J].Oceanography,2014,27(3): 32—43.doi.10.5670/oceanog.2014.66.
22 Sündermann J.The semi-diurnal principal lunar tide M2in the Bering Sea[J].Deutsche Hydrografische Zeitschrift,1977,30(3):91—101.
23 Mofjeld H O.Recent observations of tides and tidal currents from the northeastern Bering Sea shelf[R].NOAA Tech.Memo.ERL PMEL-57,1982.
24 Mofjeld H O.Observed tides on the northeastern Bering Sea shelf[J].Journal of Geophysical Research: Oceans,1986,91(C2):2593—2606.
25 Li P L,Zhou J,Li L,et al.Tidal energy fluxes and bottom boundary layer energy dissipation in the Bering Sea[J].Journal of Marine Science and Application,2010,9(3): 340—346.
26 Danielson S,Kowalik Z.Tidal currents in the St.Lawrence Island region[J].Journal of Geophysical Research: Oceans(1978—2012),2005,110(C10): C10004.
27 Kowalik Z,Matthews J B.The M2 tide in the Beaufort and Chukchi Seas[J].Journal of Physical Oceanography,1982,12(7): 743—746.
28 Mellor G L,Yamada T.Development of a turbulence closure model for geophysical fluid problems[J].Reviews of Geophysics,1982,20(4): 851—875.
29 Galperin B,Kantha L H,Hassid S,et al.A quasi-equilibrium turbulent energy model for geophysical flows[J].Journal of the Atmospheric Sciences,1988,45(1): 55—62.
30 Smagorinsky J.General circulation experiments with the primitive equations: I.The basic experiment[J].Monthly Weather Review,1963,91(3): 99—164.
31 Lefèvre F,Le Provost C,Lyard F.How can we improve a global ocean tide model at a regional scale? A test on the Yellow Sea and the East China Sea[J].Journal of Geophysical Research: Oceans,2000,105(C4): 8707—8725.
32 Kowalik Z,Proshutinsky A Y.Diurnal tides in the Arctic Ocean[J].Journal of Geophysical Research: Atmospheres,1993,98(C9):16449—16468.
33 Kowalik Z,Proshutinsky A Y.The Arctic ocean tides[M]//Johannessen O M,Muench R D,Overland J E.The Polar Oceans and Their Role in Shaping the Global Environment.Washington,DC: American Geophysical Union,1994.
34 Murty T S.Modification of hydrographic characteristics,tides,and normial modes by ice cover[J].Marine Geodesy,1985,9(4):451—468.
35 Kowalik Z.Bering Sea tides[M]//Loughlin T,Ohtani K.The Bering Sea: Physical,Chemical and Biological Dynamics.Fairbanks:Alaska Sea Grant Press,1999: 93—127.

