暴露数学思维过程的课堂教学研究——透过培养学生数学核心素养的视点

☉淮北师范大学数学科学学院 张 昆

☉江 苏 扬 州 中 学 张乃达

数学新课程理念认为，数学知识来源于主体思维活动的结果，因而数学教学就是教师引导学生数学思维活动的教学，在这种理念指导下，在数学课堂教学中，自然要竭尽所能地促进学生将发生数学思维活动的原创性过程暴露出来.数学教学实践也已经证明，真实的数学思维过程是数学教学中最有意义、最能实现数学课程资源教育价值的策略与手段，借助于数学课程资源启发学生探究发现活动的思维过程，是学生必备的核心素养之一.因此，在数学课堂教学中，促进学生暴露自己关于发生数学认识的思维过程具有重要意义，也是我们教师需要考虑与努力的一个重要的方向性目标.

一、掩盖思维活动过程在现实数学教学实践中的具体体现及其原因与危害

在数学课堂教学中，遮蔽或掩盖数学活动中的思维过程是数学教学中的不良倾向的共同本质.例如，满堂灌、注入式的要害就在于根本不承认思维活动过程的教育价值；题海战术则是使用增加知识量的方法来替代思维能力的不足，从而避开发展数学思维这一艰巨的课堂教学任务；至于在数学公开课中所表现出来的广泛的形式主义的倾向，则是遮蔽数学思维活动过程的表现.一般来说，掩盖数学思维过程的具体表现主要有如下几种：其一，忽视概念的萌生过程；其二，忽视结论的发现过程；其三，忽视方法的形成过程；其四，忽视问题的提出过程；其五，忽视规律的揭示过程.

产生掩盖思维活动过程的原因出自于两个方面.其一，数学教师自己思想认识上的偏差.有些教师害怕学生提问而导致教师“挂黑板”（特别是在公开课上），于是，在课堂上（特别是在公开课上）不敢让学生（特别是数学比较差的）回答问题，害怕自己被学生问住，故而，不敢让学生提出问题.其二，由于课堂教学时间是最可贵的，教师在课堂教学中稍有不慎就可能打乱教学预案设计好的时间安排，暴露学生思维活动过程的教学往往致使教师在课堂上不能精确地掌控教学时间，从而导致拖堂.［1］

因此，不少教师的课堂教学方式犹如一潭死水，死气沉沉，掀不起半点涟漪，整个课堂教学过程看不到思维的火花，甚至根本不存在积极的数学思维.这种教师在教学活动过程中不敢暴露甚至于尽其可能掩盖数学思维活动过程的现象，致使数学课堂教学成了一场场精心编导的演出，学生就像木偶戏中的“木偶”一样，一个个被教师牵动着在做着被动的活动，使数学课程资源发挥不了自身的教育价值，教师在课堂教学预设时所设定的目标也就形同虚设了.

二、课程教学中暴露思维活动过程示例

充分暴露数学思维活动过程的课堂教学，是对良好的教学方式、方法的概括与总结，也是许多先进的教学方法的出发点.如发现式教学把培养学生的探究式思维方式作为教学根本目标，透过模拟数学家在科学研究中的发现过程来保证在课堂上充分暴露思维活动的目的；单元教学法则为打破传统教学中课时划分的局限，在突出数学知识结构的同时，为探究思维活动的展开提供了广阔空间，为暴露数学思维的宏观过程创造了条件；启发式教学则通过数学教师的主导，发挥学生的主体地位，启发学生在课堂上进行积极的思维活动，从而达到暴露思维活动过程的目的.如果不了解这些良好的教学方法产生的指导思想，局限于对某些教学方法的程序的僵死的模仿，有时就会不自觉地在教学中掩盖学生的思维活动过程.

理在用中方知妙，再好的理论不能被广大数学教师转化为实践的动力，理论就是不结果实的花儿，是没有生命力可言的.数学知识的形式往往是从概念（定义）出发，过渡到定理，教科书的安排常常也是如此，从概念到定理再到例、习题，教师长时间受此熏陶，对此已经司空见惯、习以为常了.如此，在课堂教学活动中，教师往往只是执行教科书的安排，致使在数学概念的课堂教学中，暴露思维活动过程大打折扣.

（一）暴露萌生概念的数学思维活动过程.

数学概念教学中，教师必须仔细思考，精心设计预案，在课堂上执行预案的过程中，应随着学生思维活动的具体情况，及时、合理地加以调整.我们看萌生“二元一次方程组的解”这个例子.

例1兔子野鸡三十九，一百只脚地上走，问你辛苦狩猎人，多少野鸡多少兔（.我国古代《孙子算经》上的问题）

师：大家首先预习教科书［2］P99～106，看看可否找到解决这个问题的方法.

生1：可以通过列方程组的方法解决问题.设兔为x只、鸡为y只，由题意，可列出如下的方程组：

师：如何求这个方程组的解？

生2：首先化简方程②，将方程②的两边都除以2，即②÷2，得2x+y=50 ③.

师：接下来怎么办？

生3：由于方程①与②中的x与y分别表示这个具体问题中的兔的个数与鸡的个数，于是，x与y虽然在两个方程中，实际上是指同一个数，所以可以将方程③的左右两边同时减去方程①的左右两边，即：③-①，得x＝11.

答：鸡28只，兔11只.

教科书上就是首先定义了“二元一次方程组的解”，但是，教科书在呈现教学内容时，如同例1一样，在说明为什么可以使用加减消元法时，没有运用“二元一次方程组的解”这个概念，确实，采用鸡兔的具体脚数的事实，来说明加减消元法的使用是正确的原因，这大大损伤了发挥“二元一次方程组”课程资源的教学价值.对于学习者而言，如此教学没有进入他们的核心素养，因为，这只是借助于“实物”的具体数量在“实用性”思维层次上进行的思考活动，而不是基于数学“抽象”在“理性”思维层次上的思考活动.为了解决这个问题，我们出示抽象的方程组：

例2解方程组

师：如何解这个方程组？

生5：由⑤得x=3-2y ⑥.

把⑥代入④，得2（3-2y）+3y=-7，则-y=-13，y=13.

把y=13代入⑥，化简得x=-23.

师“：把⑥代入④”为什么可以实现呢？

生6：这是“代入消元法”所规定的.

师：听清楚我的问题，我所问的正是“代入消元法”为什么可以实现？

生：……

师：在“鸡兔同笼”问题中，是怎样实现“代入消元法”与“加减消元法”的？

生7：那里，所设的x与y是分别指那个问题中的兔数与鸡数，于是，两个方程中的x是同一个数，y也是指同一个数，因此，可以使用“代入消元法”与“加减消元法”.例2这个方程组却没有说明方程④与方程⑤中的x与y分别指同一个数……

师：生7的分析非常有道理.因此，使用“代入消元法”与“加减消元法”求解这个方程组的解就成问题了.怎么办？

生：……

师：书到用时方恨少，事非经过不知难.大家阅读“3.3消元解方程组［1］”这一页（第95页）的教学内容，看看可否解决这个问题.

生8：我看到了“使二元一次方程组中的每个方程都成立的两个未知数的值，叫作二元一次方程的解”.由于这种定义的规定，我们知道，方程组中两个方程的相同的未知数的值是相同的，因而，可以使用“代入消元法”与“加减消元法”求方程组的解.

笔者的课堂教学过程，活生生体现了“二元一次方程组的解”这个概念的萌生过程，伴随着这一过程，学生可以体会到从“实用性”思维过渡到“理性思维”的心路历程.其实，解决数学问题具有两个不同的层次，一个是事实性的层次，以“实用性”思维为支点，一个是抽象性层次，以“理性”思维为支点，因此，“二元一次方程组的解”这个核心概念萌生构成了“代入消元法”与“加减消元法”的逻辑起点，也是培养学生理性思维的关键性环节.理性思维是一个人必不可少的素养之一，是重要的核心素养，因而是数学课堂资源的重要教育价值所在.从“实用性”思维上升到“理性”思维是教学教育的一项非常重要的任务，如果数学教师对此具有清晰的认识，或早或迟总是可以或多或少地完成这项教学任务.

（二）暴露发现结论的数学思维活动过程.

在“勾股定理”的课堂教学中，有教师采用了如下的教学途径.其一，教师给每个学生发放一张坐标纸（内含同一面积单位），在坐标纸中先给出一个边长为3、4、5的特殊的直角三角形（有的教师选择使用等腰直角三角形，指导学生作以下同样的操作活动）.其二，次第以这个直角三角形的边为边长分别向这个直角三角形外画三个正方形，指导学生（通过坐标纸的方格数）分别数出这三个正方形的面积，从三个正方形面积的数据出发，启发学生猜想出32+42=52，即直角三角形两直角边的平方和等于斜边的平方.其三，再将边长为3、4、5的直角三角形一般化，得到了一般性的结论.其四，直接出示赵爽的“勾股圆方图”，带领学生对这个一般性的结论加以确证.

这种课堂教学活动恰恰遮蔽了学生在课堂上发现勾股定理这个命题产生的思维活动过程，这是因为：其一，不论是边长为3、4、5的特殊的直角三角形还是等腰直角三角形，都是教师提供的，不是学生提出来作为探究活动的基础的；其二，向形外作正方形也是教师要求学生去做的，而不是学生自己心理上产生这样的操作行为的欲望；其三，验证勾股定理的“勾股圆方图”也是教师直接提供给学生的，不是学生自己为了证明这个结论而探究发现的.由此可见，这样的课堂教学活动，主要是教师在课堂上向学生提供关键性的探究与思考的环节，同时，忽视了问题的提出过程，只是教师讲解学生记录的教学方式罢了.笔者通过思考，在课堂教学中，设计了如下的教学活动过程：

［环节一］

师：由于种种原因，古人特别喜欢使用面积来表示（或证明）代数恒等式，请你设计一个图形，表示完全平方式（a+b）2=a2+2ab+b2.

生1：可以构建一个边长为a+b的正方形，如图1，就可以达到目的.

［环节二］

师：能够构造一个说明完全平方差公式（a-b）2=a2-2ab+b2的几何图形吗？

生2：可以，只要将图1变成图2，就可以达到达到目的.图2中的面积关系为：（a-b）2=（a+b）2-4ab=a2-2ab+b2，这正是完全平方差公式.

图1

图2

图3

［环节三］

师：假如要研究一个直角边长分别为a、b，斜边长为c的直角三角形的三边关系，可以借助上述研究结果中的图形吗？

生3：可以.分别连接图2中四个矩形的对角线，得到图3，去除图3中外围四个4直角三角形，就可以得到图4.图4中的四个直角三角形与一个正方形之间的面积关系，可以用一个代数式表示为即c2=a2+b2.

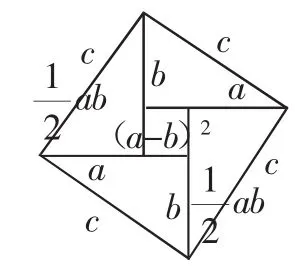
图4

图5

师：这就是今天我们要学习的勾股定理的内容：直角三角形两直角边的平方和等于斜边的平方.［3］

这种从提出问题到发现数学命题的结论，再到验证结论的过程，是借助数学课程资源培养学生的核心思想之一，教师对此必须具有清醒的认识.赵爽在为《周髀算经》“勾股圆方图”作注中写道，“案弦图又可以勾、股相乘为朱实二，倍之为朱实四，以勾股自差自乘为中黄实.加差实亦成弦实”［4］（这里的“实”用现代语说就是指图形的面积——引者注）.如图5，教科书为了帮助教师施教、学生学习，在验证勾股定理时，直接给出了图5所示的结论.如何构建出图5，具有极其重要教育价值，它的实现，教师非细心地把握学生构建时的心理活动不可.很多教师就只是忠实地执行了教科书对课堂教学的提示活动，而没有将注意力集中到如何通过课堂教学活动启发学生构造出赵爽的“勾股圆方图”的心理过程，笔者的课堂行为正是借助于数学史知识的辅助，实现了启发学生构造出“勾股圆方图”的课堂教学活动过程.

然而，通过反思认识到，笔者的这种课堂教学过程其实也不尽如人意，这其中的重要一点，就是问题的提出过程基本上是笔者奉献给学生的，因此，这种课堂教学活动也有待于进一步完善，但是，笔者到目前为止，还没有寻得一种好的办法解决这个问题.不过，既然已经发现了问题，在笔者不断思考与努力下，总会有解决的可能性.在此，也希望读者予以关注与思考，以此达到逐步完善它的目的.

（三）暴露发现思路的数学思维活动过程.

在前述勾股定理的证明活动中，我们已经发现了部分教师只是将证明过程提供给学生，造成了教学的巨大损失.在数学解题教学中，也会出现同样的弊端，教师往往忽视（略去）解决问题思路的探究活动过程，而只是将自己通过探究活动发现的结论字斟句酌地奉献给学生，致使学生能够读懂结论中的某些关键性环节的结构组成，理解其逻辑体系，而不知道这些环节是如何获得的，整个逻辑体系是怎样组建起来的，这就是典型的掩盖了发现、解决问题思路的思维活动过程.我们看实际课堂教学中的一个例子.

“这个场景和毕赣最喜欢的导演塔可夫斯基的电影片段相似，毕赣是在这个场景中利用杯子向塔可夫斯基致敬。看过塔可夫斯基的观众当然明白，然而大部分观众却是不清楚的。”沙丹说。

例3 求证：两边及其第三边中线对应相等的三角形全等.

已知：如图6，在△ABC与△EFG中，AB=EF，AC=EG，AD=EH，求证：△ABC≌△EFG.

图6

在这个例题的课堂教学中，有教师就直接把证明过程抄写到PPT上（本文限于篇幅略去不记），而不讲辅助线是如何出现的，几组全等三角形是如何组成一个环环紧扣的逻辑体系的，这种逻辑体系如何最终得以精致的表达，导致学生只有经由记忆的途径来学习这道题的解决.这就掩盖了解决问题的探究发现活动过程，造成了课堂教学的损失.笔者在课堂教学中，对此加以改进（省略号表示学生思维活动的中断）：

师：如何发现这道证明题的思路？

生：……

师：条件是AB=EF，AC=EG，由“边角边”或“边边边”公理，要么证明AB、AC的夹角∠BAC与EF、EG的夹角∠FEG对应相等，即∠BAC=∠FEG ①，要么证明第三组边BC、FG对应相等，即BC=FG ②.然而，从已知中找不出这样的条件.怎么办？

生1；老师您的分析使我认识到，必须将相等的中线这个条件转化为两边的夹角相等，或转化为第三边相等.

生2：由于条件没有牵涉角的相等关系，所以寻找对应角相等是不可能的，因此，我想只有考虑转化为某两个三角形的三组对应边相等.

师：好想法.如何转化为三组对应边相等？

生3：我想将线段AB（与EF）转移到它需要的地方去，与此同时，又可以使用上条件AD=EH.

师：生3不再是对两个图形进行的理论上的想法了，而是非常具有操作性的想法.怎样才能如愿以偿？

生4（笔者在黑板上记录与整理，并相应进行了板书设计）在△ABD中，由于点D是BC的中点，可以考虑构造全等三角形将线段AB转移到与AC的一个端点相交.具体而言，延长AD到点M，使DM=DA，连接CM，由对顶角相等，知∠ADB=∠MDC.又由已知DB=DC，由“边角边”公理，知△ABD≅△MCD，从而CM=AB，∠DAB=∠DMC③.在△EFG中，也做同样的操作，可得GN=EF，∠HEF=∠HNG ④.于是，在△AMC与△ENG中，由于AC=EG（已知），CM=GN（已证），AM=2AD=2EH=EN，故由“边边边”公理，知△AMC≅△ENG，则∠AMC=∠ENG ⑤，∠HEF=∠HNG ⑥.由③④⑤⑥，知∠BAC=∠FEG成立.于是，在△ABC与△EFG中，由于AB=EF，∠BAC=∠FEG，AC=EG，由“边角边”公理，知△ABC≌△EFG.（在课堂上，将生4探究思考的结果转化为证明的表达过程使用了PPT展示，这里略）

笔者的课堂教学活动过程体现了：其一，辅助线的萌发过程，在这里作了大量的铺垫与渲染，是促使学生步步逼近解决问题关键环节的核心；其二，竭尽所能促使学生暴露发现证明思路的分析活动的思维过程.其实，从“勾股定理”与例3的解决问题的探究活动思维过程中，我们可以发现，数学解题活动是极具创造性的课程资源，甚至比数学概念、原理更具培养学生创造性的教学价值，学生由探究稍微复杂些的数学问题，可以感受到更直观的体验.［5］问题是，教师如何启发学生通过探究发现解决问题的思路，要全心全意暴露学生探究思路的思维活动过程.这种探究思路的过程是重要的数学核心素养之一，它可以直接应用于解决生活、生产与科学研究中去.

三、简要结语

以培养学生数学核心思想为数学教学的总目标，以暴露数学思维活动过程为实现这项目标的重要手段，构成了设计数学教学活动程序的依据与基础.设计数学教学程序本身也是一件创造性的工作，充分暴露数学思维活动过程是数学教学设计的指导性观念之一，教师只要具有充分暴露数学思维活动过程的教学愿望，又能根据客观知识的结构性特点与具体学生发生数学认识时的思维活动特点，假以时日，深入思考与反思，就一定会依据知识性质与学生的学习水平设计出适合学生的教学程序预案，保证课堂教学的成功，发挥数学课程资源的价值，培养学生的核心素养.

1.张乃达.数学思维教育学［M］.南京：江苏教育出版社，1990.

2.《新时代数学》编写组（吴之季、张孝达主编）.义务教育课程标准实验教科书·数学·七年级（上册）［M］.上海：上海科学技术出版社，2012.

3.张昆，张乃达.论数学教学创新设计［J］.中学数学（下），2016（8）.

4.刘钝.大哉言数［M］.沈阳：辽宁教育出版社，1993.

5.张昆，罗增儒.数学解题教学设计研究——指向渗透数学观念的视点［J］.中学数学杂志，2017（11）.