拖拉机前轴悬架参数优化设计

袁加奇，范 骏，周永清

（1.江苏开放大学 江苏城市职业学院，南京 210036； 2.南京农业大学 工学院，南京 210031）

车辆在行驶过程中，车轮受到路面不平度激励而激起的车体振动是较为剧烈的，尤其是轮式农用拖拉机经常行驶在较差的路面条件下。路面不平度所激起的拖拉机振动不仅会让驾驶员身体感到不适，危害到驾驶员的身心健康，而且容易让驾驶员产生驾驶疲劳从而降低工作效率，更严重的还会影响到拖拉机的操纵安全性，容易导致拖拉机事故的发生，所以对拖拉机的振动特性研究尤为重要[1–2]。

由于受到国内经济发展及制造水平的制约，国产拖拉机的减振技术水平相对落后，也并没有引起足够的重视，目前我国生产的大多数拖拉机基本上是无悬架刚性结构，没有任何的减振装置，拖拉机的振动较为剧烈，乘坐舒适性远远低于道路车辆。而在欧美等发达国家，由于在拖拉机上同时安装了驾驶员座椅悬架、驾驶室悬架、前轴悬架、后轴悬架以及全悬架等减振装置，大大降低了拖拉机的振动强度，乘坐舒适性、行驶平顺性和操纵稳定性等性能远远高于国产拖拉机。座椅悬架是拖拉机上的重要减振装置，它是拖拉机与驾驶员直接接触的部件，座椅悬架为驾驶员提供舒适乘坐环境和操纵稳定安全的工作条件[3]。前轴悬架是直接影响拖拉机前轮与地面接触情况的部件，对于拖拉机的转向性能和操纵安全有十分重要的作用。意大利Martelli等运用ADAMS动力学仿真软件平台对安装前轴悬架轮式农用拖拉机的行驶安全性和乘坐舒适性进行了仿真研究分析，研究结果表明装有前轴悬架的拖拉机可以改善拖拉机的行驶安全性和乘坐舒适性，但效果并不明显，而且改善效果取决于拖拉机的实际行驶条件[4]。Mazhei等的研究结果表明，当拖拉机的前端悬挂农具工作时，安装前轴悬架拖拉机的减振效果较为明显，并且减振效果的好坏还取决于前轴悬架刚度系数和阻尼系数的匹配情况[5]。Lehtonen等的研究结果表明在拖拉机上安装前轴悬架能够明显降低拖拉机的横向振动强度，而对于拖拉机垂向和纵向的振动强度影响并不明显[6]。

本文通过理论分析建立拖拉机的平面振动数学模型，运用MATLAB/SIMULINK仿真平台建立拖拉机的振动仿真模型，主要研究拖拉机前轴悬架的刚度和阻尼参数对轮式农用拖拉机振动特性的影响，并利用MATLAB优化工具箱仿真优化设计前轴悬架的刚度系数和阻尼系数的匹配。为提高国产拖拉机的减振技术水平，降低拖拉机在较差路面条件下行驶时的振动强度以及为国产轮式农用拖拉机前轴悬架系统的参数匹配设计提供重要的理论研究基础。

1 拖拉机振动模型的建立

轮式农用拖拉机振动系统的空间自由度较为复杂，为了简化振动特性的理论研究，将拖拉机整体结构及悬架系统简化为关于拖拉机中心面的左、右对称结构，并且假设拖拉机的左、右车轮在同一路面不平度条件下行驶，只是前、后车轮的路面激励存在一定的时间差△t，即拖拉机的后车轮受到的路面不平度激励比前车轮受到的路面不平度激励滞后一个时间差。考虑到拖拉机车轮和路面不平度激励之间是弱耦合系统[7–8]，理论研究和软件仿真研究时可以忽略动弯沉量对拖拉机各部位振动特性的影响。

由于考虑到拖拉机整机系统结构的对称性，可以将装有前轴悬架和座椅悬架系统的轮式农用拖拉机结构简化为二分之一整车的4自由度平面振动模型如图1所示。

根据牛顿第二运动定律可得前轴悬架拖拉机4自由度系统的平面振动微分方程式（1）。

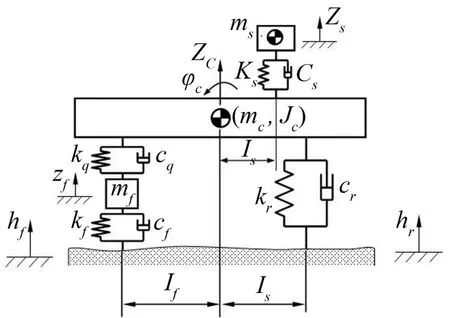
图1 前轴悬架拖拉机4自由度平面振动模型

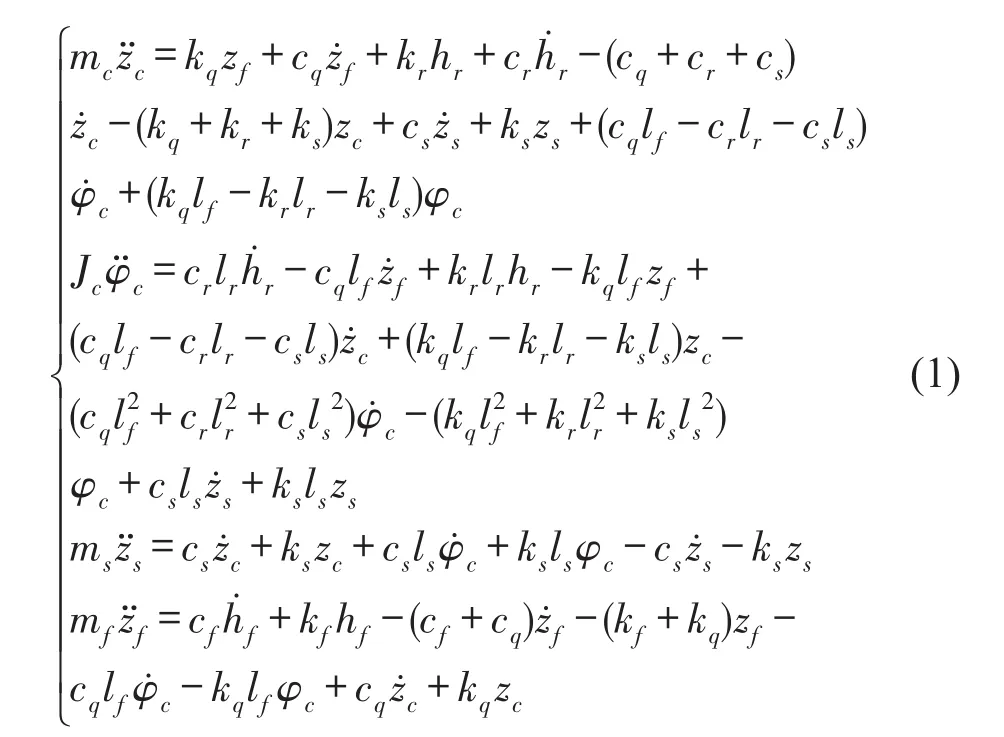
式中mc、ms、mf—拖拉机整车总质量、座椅悬架的簧上质量和前轴系统的质量，kg；Jc—拖拉机机身绕质心处的俯仰转动惯量，kg∙m2；kf、kr、ks、kq—前轮胎刚度系数、后轮胎刚度系数、座椅悬架刚度系数和前轴悬架刚度系数，N∙m-1；cf、cr、cs、cq—前轮胎阻尼系数、后轮胎阻尼系数、座椅悬架阻尼系数和前轴悬架阻尼系数，N∙s∙m-1；lf、lr、ls—拖拉机前、后车轴中心位置和座椅质心位置至拖拉机机身质心处的水平距离，m；hf、hr—拖拉机前、后车轮受到的随机路面不平度激励的垂直方向位移，m；zc、φc、zs、zf—拖拉机机身质心处垂直方向位移、机身质心处俯仰方向角位移、座椅质心处垂直方向位移、前轴悬架垂直方向位移，m。

将式（1）的振动微分方程式转换为矩阵形式

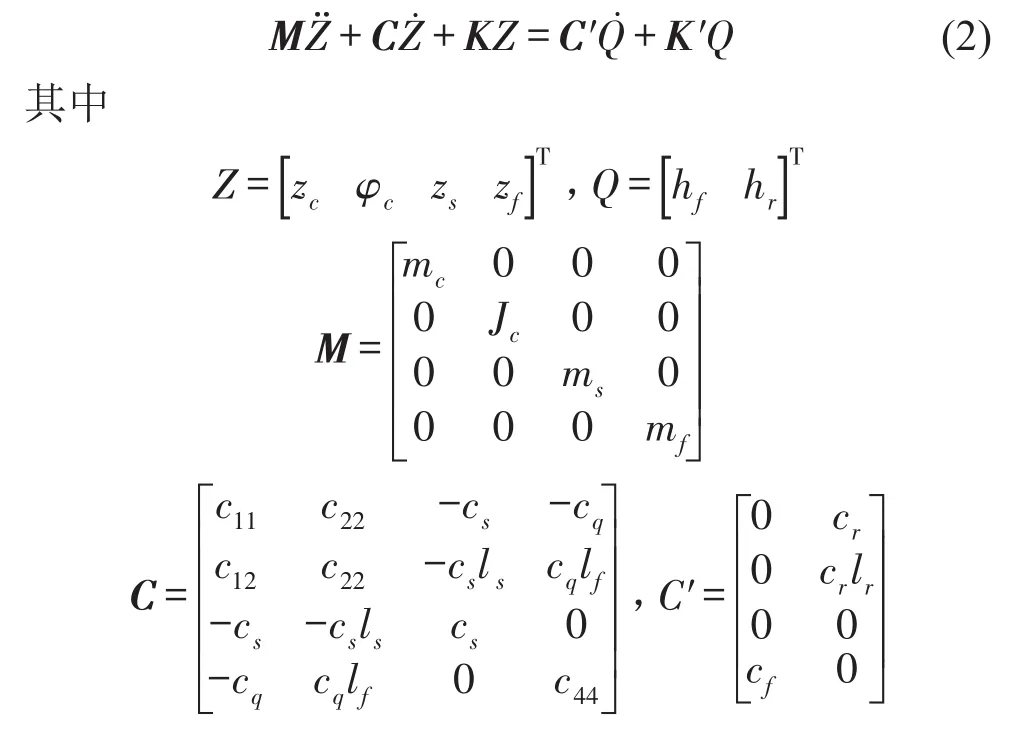
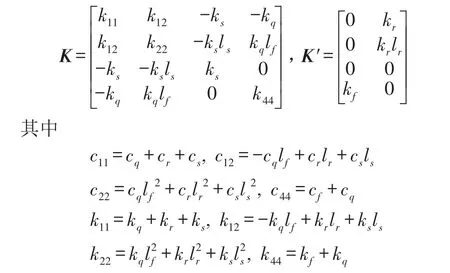
将式（2）改写成控制状态空间方程形式

2 拖拉机参数的获取

为获取常发CF700型轮式农用拖拉机的主要振动特性性能参数，在自主研制的测试试验台架上对拖拉机尺寸参数、质量参数、转动惯量参数、轮胎刚度系数以及阻尼系数等参数进行测量、测试和计算[9–10]，得到拖拉机的主要性能参数如表1所示。

依据文献研究中关于车辆悬架偏频及静挠度的选择原则[11–12]，并结合常发CF700型轮式农用拖拉机的实际工作条件，选取拖拉机前轴悬架的偏频为1.5～3.0 Hz，由车辆悬架的偏频公式可得式(4)。

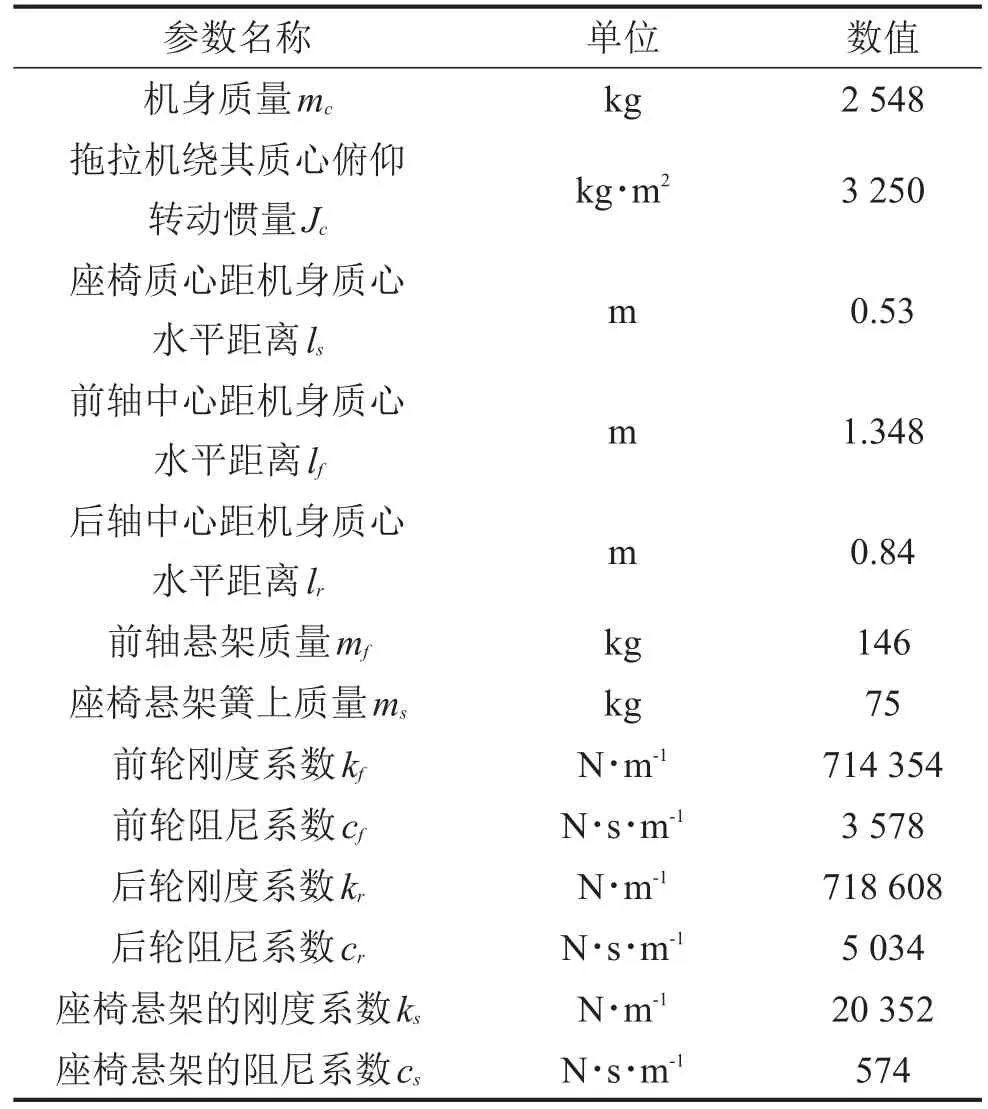
表1 CF700型拖拉机主要参数

式中m——前轴悬架的簧上质量，kg

由式(4)可得

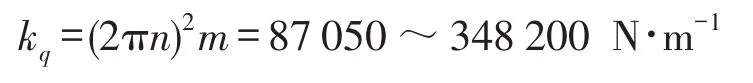
根据车辆的振动理论研究和实际工程经验，当路面不平度激励等级为D级时，一般选择悬架系统的阻尼比ζ=0.15～0.45，则可得拖拉机前轴悬架系统减振器的阻尼系数为

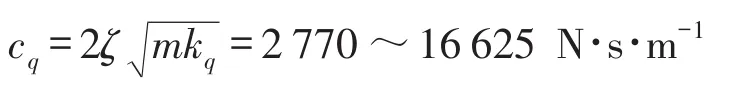
3 仿真模型的建立与验证

3.1 随机路面激励模型

拖拉机行驶路面的随机输入是分析无悬架拖拉机在时域或频域内的性能的重要参数。本文采用MATLAB/SIMULINK仿真软件产生的积分白噪声随机路面模型作为路面不平度激励，当拖拉机以恒定速度行驶时，拖拉机行驶速度的时域功率谱密度即为白噪声信号，时域功率谱密度为常数4π2Gq(n0)n02v，因此随机路面不平度激励的轮廓可由时域功率谱密度为的白噪声信号通过积分器产生得到，即

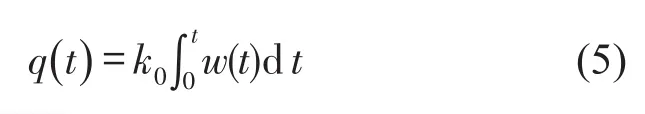
w(t)——单位白噪声。

当拖拉机行驶的随机路面不平度激励等级为D级时，随机路面的不平度系数为Gq(n0)=1 024×10-6m2，随机路面不平度激励信号的方差为n0=0.1 m-1，当拖拉机行驶速度为10 km/h时，利用MATLAB/SIMULINK仿真软件构造出随机路面不平度激励的白噪声信号模型，通过白噪声信号仿真模型产生的随机路面不平度激励的垂直方向位移轮廓如图2所示。

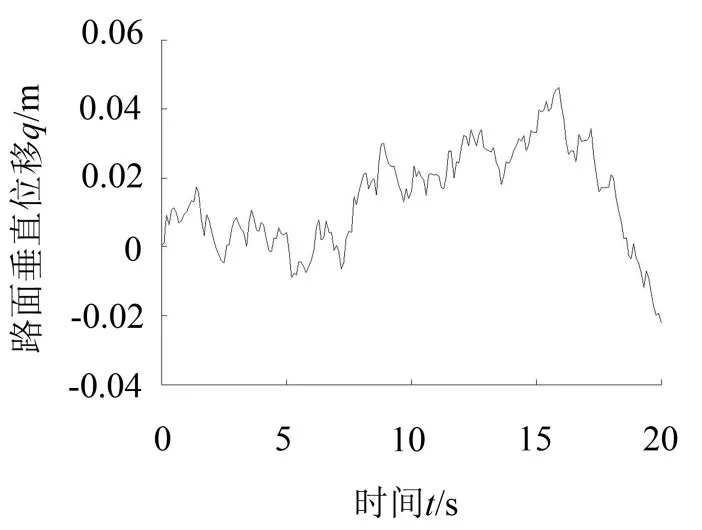
图2 积分白噪声随机路面轮廓

3.2 仿真模型的验证

为验证所建立的拖拉机系统平面振动仿真模型的可靠性，在GB/T 10910-2004规定修建的100 m较平滑标准试验路面跑道上进行拖拉机匀速行驶时的振动测试试验。振动测试试验时拖拉机在二档位工况速度下行驶，通过测试测得拖拉机二档位工况下行驶的前进速度为7 km/h。拖拉机振动测试系统包括用于采集并记录振动测试信号的LMS SCADAS Mobile便携式动态信号测量仪一台。CA-YD-185TNC型压电式单向加速度传感器3个，单向加速度传感器通过磁盘吸力分别安装固定在拖拉机前轴中心位置正下方、后轴中心位置正下方以及座椅底板中心位置处。测试用安装LMS测试软件的笔记本电脑一台用于分析振动信号。拖拉机振动试验测试系统以及加速度传感器在拖拉机机身上的安装部位如图3所示。

图3 拖拉机振动测试系统

图4所示为轮式农用拖拉机各部位垂直方向位移几何关系的平面模型，可以得到拖拉机前轴中心位置的垂直方向位移zf、后轴中心位置的垂直方向位移zr和拖拉机机身质心处的垂直方向位移zc存在以下关系式（6）所示[13]。

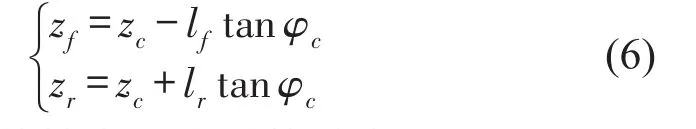
式中zf—拖拉机前轴中心位置的垂直方向位移，m；zr—拖拉机后轴中心位置的垂直方向位移，m；zc—拖拉机机身质心位置的垂直方向位移，m；zs—座椅底板位置的垂直方向位移，m。lsr—座椅质心处至后轴中心位置的水平距离。

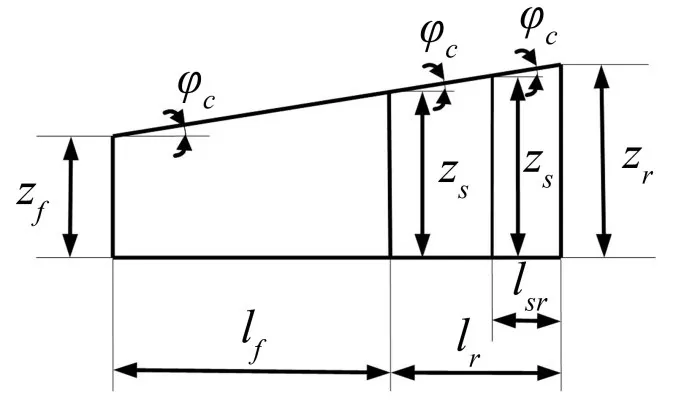
图4 垂直位移的几何关系

由于拖拉机机身俯仰方向的振动角位移φc较小，可近似 tanφc≈φc，则式（6）可简化写为

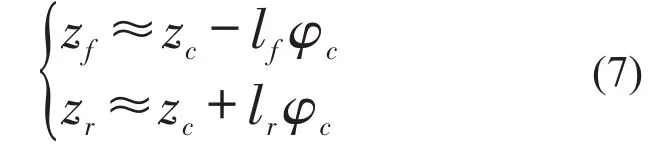
由式（7）可知，通过振动试验测得拖拉机前、后车轴中心位置的垂向振动加速度可近似计算出拖拉机质心处垂向振动加速度和俯仰方向角振动加速度。拖拉机各部位的振动测试试验结果与计算结果见图5－图8。

图5 前、后轴垂向振动加速度变化曲线

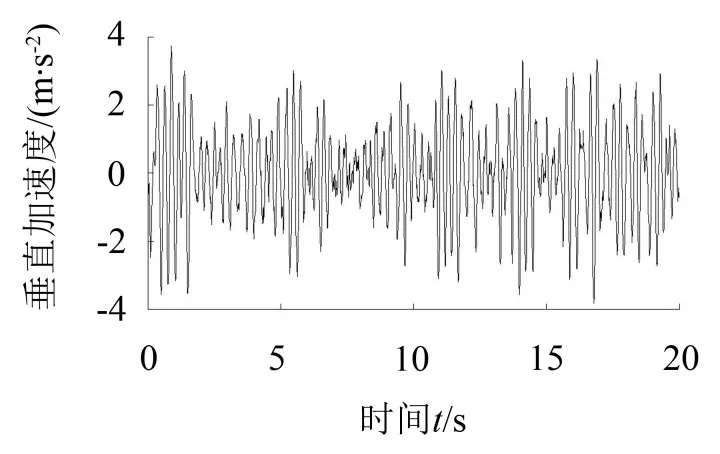
图6 机身质心处垂向振动加速度变化曲线

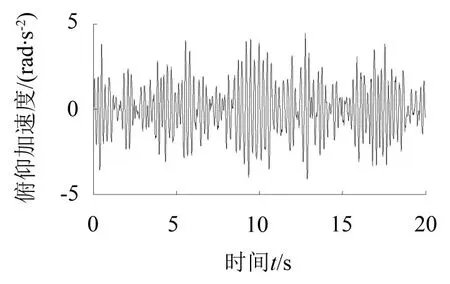
图7 机身质心处俯仰角振动加速度变化曲线

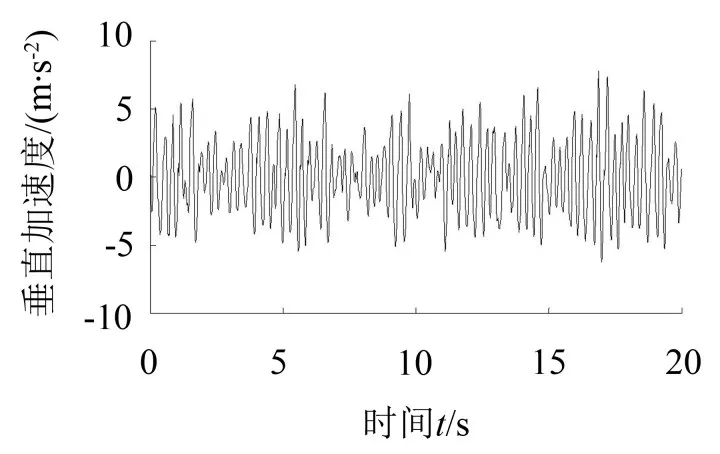
图8 座椅垂向振动加速度变化曲线

将拖拉机行驶在标准试验路面上的振动试验测试结果与在同等条件下的振动模型仿真结果对比见表2。仿真时拖拉机振动模型的主要参数为表1中没有安装前轴悬架轮式农用拖拉机的主要性能参数。

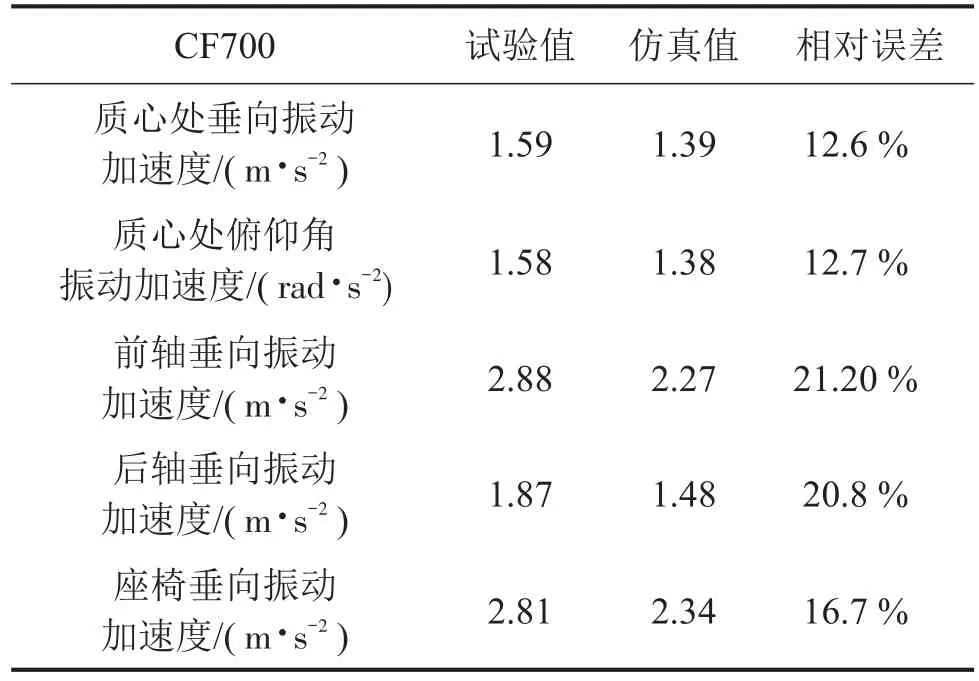
表2 试验结果与仿真结果对比

由表2中试验结果与仿真结果的对比情况可知，振动试验测试结果中拖拉机各部位的振动加速度均方根值略高于振动模型的仿真结果，试验结果与仿真结果的平均误差率为16.8%。由于在建立振动仿真模型时并未考虑到拖拉机发动机振动传递到机身，拖拉机左、右车轮受到路面不平度激励不同所引起的拖拉机的横向振动以及车轮在实际工作过程中由于轮胎气压的变化而引起的刚度系数和阻尼系数的变化等多方面因素，振动模型的仿真结果与实际振动测试试验结果的误差在可接受的范围内，且振动模型的仿真结果能够真实地反映拖拉机的振动强度和振动趋势。

4 前轴悬架参数优化

4.1 目标函数

悬架系统簧上质量的振动加速度、悬架动行程以及轮胎动载荷是评价车辆悬架系统性能好坏的最重要的三个评价指标。因此分别选取拖拉机机身质心处垂向振动加速度均方根值、拖拉机机身质心处俯仰方向角振动加速度均方根值、前轴悬架簧上质量垂向振动加速度均方根值、座椅质心处垂向振动加速度均方根值、前轴悬架动行程均方根值以及前轮胎动载荷均方根值等6个参数指标作为前轴悬架系统参数优化设计的子目标函数。

4.2 设计变量

本文主要研究前轴悬架的刚度系数和阻尼系数对拖拉机平顺性的影响，只有在悬架系统中选配恰当的弹簧和减振器，悬架系统才能起到有效抑制车身振动的作用，并保证拖拉机具有较好的行驶平顺性。因此，在对前轴悬架系统进行优化设计时，选取前轴悬架刚度系数和阻尼系数为优化配置的设计变量。

4.3 约束条件

综上所述常发CF700型轮式农用拖拉机前轴悬架刚度系数和阻尼比的取值范围约束条件为

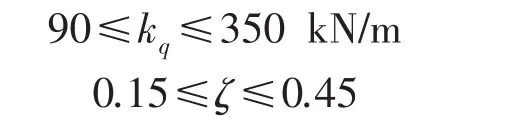
在刚度系数和阻尼比的约束条件范围内，采用逐步选优求解法，取刚度系数的步长Δk=1 kN/m，阻尼比的步长Δζ=0.05，并循环计算求解，逐步选优获得拖拉机前轴悬架刚度系数和阻尼系数的最佳配置。

4.4 仿真模型的建立

本文选择MATLAB/SIMULINK优化工具箱作为拖拉机前轴悬架刚度系数和阻尼系数的优化工具，并对拖拉机整机系统的动态振动特性进行仿真分析。通过MATLAB/SIMULINK仿真软件产生积分白噪声随机路面不平度激励模型，建立安装有前轴悬架系统的常发CF700型轮式农用拖拉机系统四自由度平面振动仿真模型，如图9所示。振动仿真模型中的输入矢量为前、后车轮受到的随机路面不平度激励，即状态方程式（3）中的A、B、C、D 4个矩阵，振动仿真模型的输出量依次是拖拉机机身质心处垂向振动加速度、俯仰方向角振动加速度、座椅位置垂向振动加速度、前轴悬架垂向振动加速度、前轴悬架动行程、前轮胎动载荷等六个振动特性参数。

4.5 优化结果分析

当拖拉机在路面不平度等级为D级路面上以前进速度为10 km/h行驶时，通过建立的前轴悬架拖拉机系统4自由度平面振动仿真模型，以及结合上述确定的优化目标函数、设计变量以及约束条件等，在MATLAB平台下编写优化函数的M文件[14]，优化仿真获得拖拉机前轴悬架系统的刚度系数和阻尼系数的最佳配置参数值。

优化仿真结果得到当前轴悬架刚度系数kq=334 kN/m，ζ=0.35，即cq=12 665 N∙s/m时，拖拉机系统的振动特性综合性能达到最优。优化结果见表3。

表3 前轴悬架拖拉机优化结果

改变拖拉机系统振动仿真模型中的状态方程矢量，在同等条件下，建立没有安装前轴悬架的刚性轮式农用拖拉机3自由度平面振动模型，仿真得到拖拉机机身质心处垂向振动加速度均方根值、俯仰方向角振动加速度均方根值、座椅底板位置垂向振动加速度均方根值和拖拉机前轮胎动载荷均方根值分别为 1.089 9 m∙s-2、1.084 2 rad∙s-2、1.829 3 m∙s-2和2.016 8 kN，安装前轴悬架拖拉机的各部位振动参数较没有安装前轴悬架时分别下降14.57%、34.31%、4.42%和17.76%，在一定程度上改善了拖拉机的乘坐舒适性和操纵安全性等多方面性能。

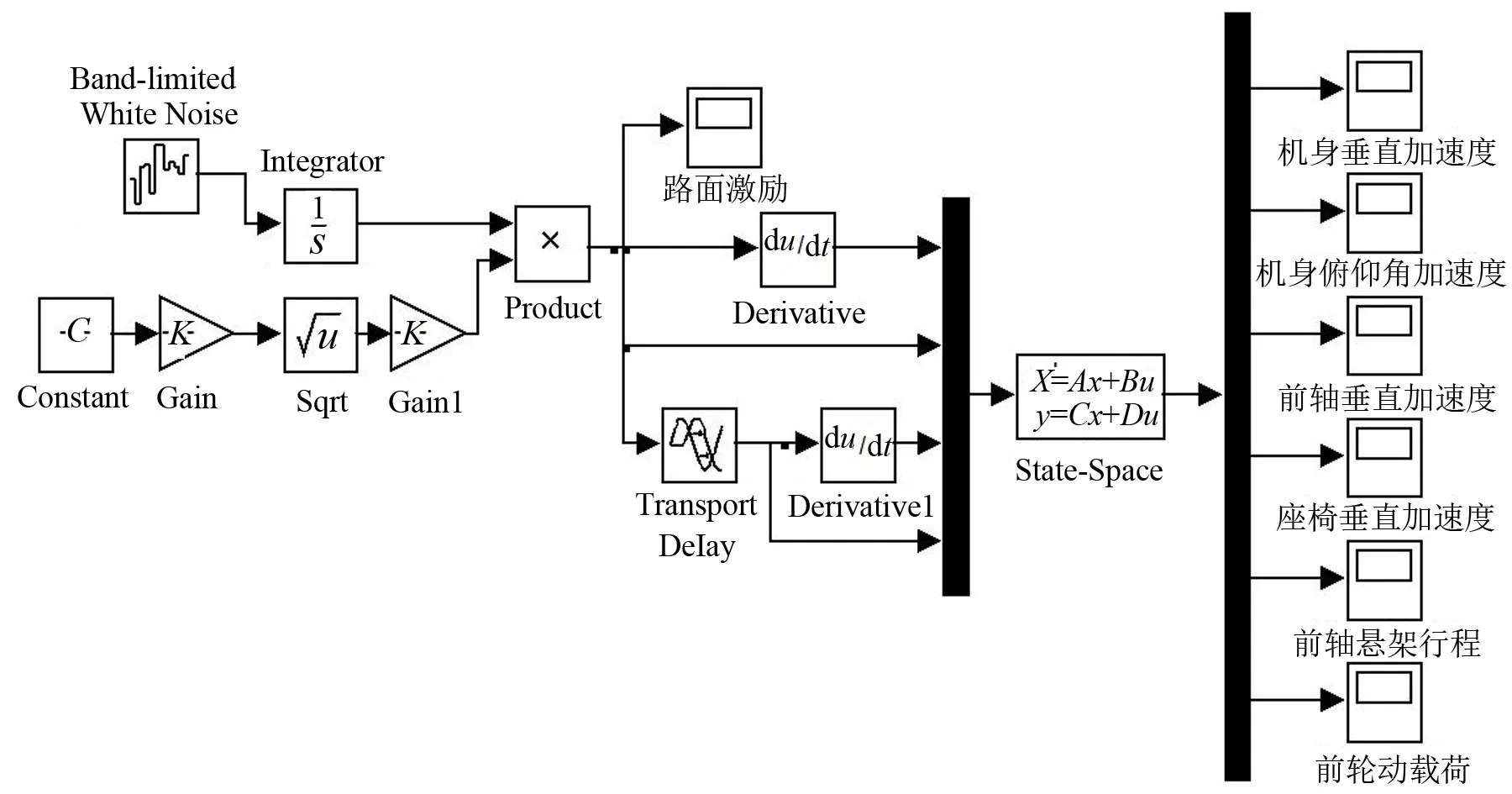
图9 前轴悬架拖拉机平面振动仿真模型

将没有安装前轴悬架拖拉机的性能参数和优化配置后获得的前轴悬架刚度系数和阻尼系数代入振动仿真模型中对比仿真分析，仿真结果得到拖拉机机身质心处垂向振动加速度值、俯仰方向角振动加速度值、座椅底板位置垂向振动加速度值以及前轮胎动载荷值随时间变化曲线分别如图10－图13所示。

图10 拖拉机质心处垂向振动加速度变化曲线

图11 拖拉机质心处俯仰角振动加速度变化曲线

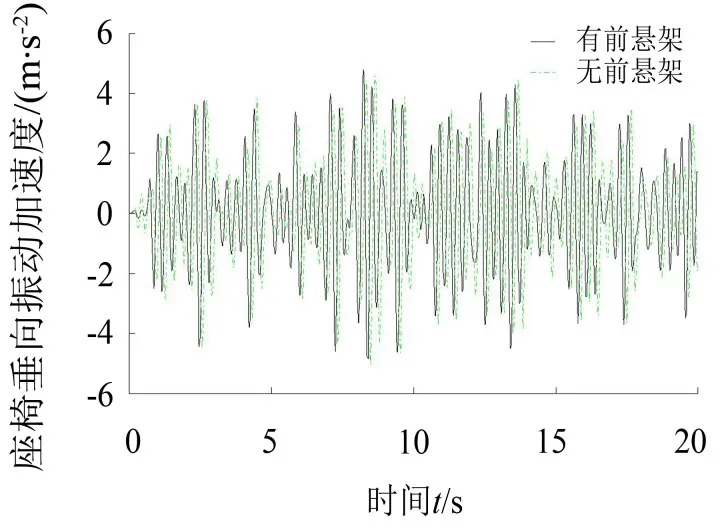
图12 拖拉机座椅垂向振动加速度变化曲线

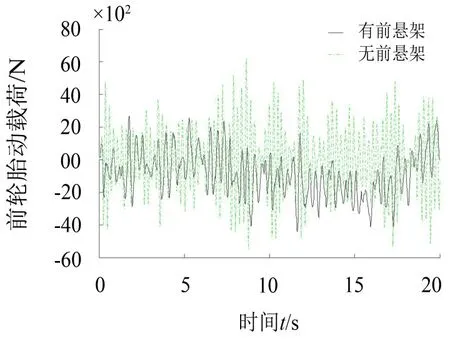
图13 拖拉机前轮胎动载荷变化曲线

5 结语

本文以常发CF700型轮式农用拖拉机前轴悬架系统参数优化设计为研究目标，运用MATLAB/SIMULINK仿真平台建立前轴悬架拖拉机系统四自由度平面振动仿真模型，仿真研究拖拉机整机系统的动态振动特性，在GB/T 10910—2004规定修建的100 m较平滑标准试验路面跑道上进行了无悬架刚性拖拉机的振动试验，并与同等条件下的振动模型仿真结果进行对比分析，得到试验结果与仿真结果的平均误差率为16.8%，综合考虑其它因素误差范围可接受，仿真结果具有一定的可靠性。在此基础上，利用MATLAB优化工具对拖拉机前轴悬架的刚度系数和阻尼系数进行优化设计，得到优化配置后的前轴悬架刚度系数和阻尼系数分别为334 kN/m和12 665 N∙s/m。安装有前轴悬架拖拉机的乘坐舒适性、行驶平顺性以及操纵安全性等各方面性能都有明显的改善。本文的研究结论为后期国产轮式农用拖拉机前轴悬架的参数匹配设计提供重要的理论研究基础。

[1]万叶青，张伟欣，杨俭，等.拖拉机机体振动分析方法及其应用[J].拖拉机与农用运输车，2005(3)：11-15.

[2]万叶青，邓彦平，李国英.拖拉机驾驶座传递振动的测量机评价[J].拖拉机，1989(1)：32-38.

[3]宋春桃.车辆座椅的磁流变液减振研究[D].南京：南京理工大学，2007.

[4]MARTELLI M,PAOLUZZI R,ZAROTTI L G.The front suspension of agricultural tractors[C].14 th International Conference of the International Society for Terrain-Vehicle Systems,Vicksburg,Ms USA October 20-24,2002.

[5]WEIGELT H.Front axle suspension for agricultural tractors[C]. Internationale Tagung Landtechnik,Braunschweig(Germany,F.R.),7-8 Nov 1985:47-49.

[6]LEHTONEN T J,JUHALA M.Predicting the ride behaviour of a suspended agricultural tractor[J].International Journal of Vehicle Systems Modeling and Testing,2005,1(1/2/3):131-142.

[7]任卫群.车-路系统动力学中的虚拟样机[M].北京：电子工业出版社，2005.

[8]FAFARD M,LAFLAMM E M.Dynamic analysis of existing continuo us bridge[J].JournalofBridge Engineering,1998,3(1):28-37.

[9]聂信天，史立新，顾浩，等.农用轮胎径向刚度和阻尼系数试验研究[J].南京农业大学学报，2011，34(5)：139-143.

[10]聂信天，史庆春，顾浩，等.拖拉机转动惯量测量及误差分析[J].机械科学与技术，2012，31(8)：1325-1328.

[11]张洪欣.汽车设计[M].2版.北京：机械工业出版社，1999.

[12]周长城.汽车平顺性与悬架系统设计[M].北京：机械工业出版社，2011.

[13]屈维德，唐恒龄.机械振动手册[M].2版.北京：机械工业出版社，2000.

[14]张德丰.MATLAB数值分析[M].北京：机械工业出版社，2012.