超声波检测焊点质量的建模方法及应用分析

何智成 汲彦军 成艾国 何道聪

1.湖南大学汽车车身先进设计制造国家重点实验室,长沙,4100822.上汽通用五菱汽车股份有限公司,柳州,545027

0 引言

点焊是连接金属薄板的一种常用方法，这种焊接方法简便易行、经济有效，而且适用于高速自动化生产，因此被广泛应用于现代制造业[1]。焊接过程中的点焊参数波动将导致焊核直径不足、虚焊,或焊核中存在飞溅、气孔、缩松、裂纹等问题[2]。点焊的质量直接影响着焊点的强度，特别是一些关键焊点，焊点质量会影响整个结构的性能[3]。

焊点质量检测主要有破坏性检测和无损检测两大类。破坏性检测存在成本较高、效率低、破坏性强等缺陷。无损检测方法中，超声波检测能进行各类焊点缺陷的识别，同时能大大降低质量控制的成本[4]。然而进口超声设备的焊点质量判定标准不透明，超声波检测无法直接应用到所有类型的焊点检测质量中。

近年来，通过定量化与数字化建立超声传播有限元模型[5]来解释和预测材料内部的缺陷，已经成为焊点质量检测的一种重要手段，国内外学者在超声传播信号处理方法及时频特征分析[6-7]等方面已有研究，但对焊点有限元建模的准确性未作深入探讨。

本文通过金相实验得到了焊点有限元模型的形状及尺寸参数，通过对焊点的超声信号分析得到了焊点有限元模型的材料阻尼系数,并建立了多种不同类型的焊点超声检测有限元模型，利用仿真模型探讨了车身曲面工况焊点检测结果的一致性。通过仿真验证分析得出：在曲面焊点检测时，超声焊点检测结果受到的影响很小，甚至可忽略。本次研究发现，焊点质量检测仿真模型可以用于建立焊点检测标准，实现焊点质量的提前预判，并为下一步实现焊点质量自动化检测提供支撑。

1 超声波检测焊点质量机理

1.1 超声信号高斯回波模型

材料或结构内部的缺陷可以通过超声波检测来识别，超声检测中的回波信号通常是一种被探头中心频率调制的宽带信号，这种信号是一种时频有限的非平稳信号，其参数化高斯数学模型如下[8]：

s(θ,t)=βe-α(t-τ)cos(2πf0(t-τ)+φ)

(1)

θ=(α,τ,f0,φ,β)

式中，α为带宽；τ为到达时间；f0为中心频率；φ为相位；β为幅值系数。

式(1)可推广到多重回波，M重回波信号的高斯模型可以表示为

(2)

θm=(αm,τm,f0m,φm,βm)

式中，θm为第m个参数矢量；n(t)为加性噪声。

1.2 超声信号特征参数

由于钢的声阻抗远远大于空气的声阻抗，所以超声波从钢中射入空气时几乎没有透射而只有反射。在超声波焊点检测过程中，由于焊核直径过小或者焊核中有气孔等都会出现非底面回波，而焊核与母材的声阻抗相差不到千分之一[9]，在母材与焊核中间不会有反射波，因此可以采用超声波对焊点的质量进行检测。

超声波在焊点中传播时，随着传播距离的增加，其能量逐渐衰减，衰减的原因主要是超声波在传播过程中被散射和吸收。焊点在检测过程中由于中间焊核的晶粒粗大，所以会引起严重衰减，焊核大小不同引起的衰减程度不一。

利用多回波信号参数估计算法[10]处理计算，可得到焊点超声信号的时域参数信息：带宽α、到达时间τ、中心频率f0、相位φ以及幅值系数β。根据这些参数信息可计算提取超声信号的时域特征值，本文提取了4个时域特征值。

(1)下层板底面回波波峰间隔S(μs或m)：反映焊接区厚度及压痕深度。

(2)底面回波幅值的衰减率：

(3)

式中，Ai为第i个下底面回波幅值。

(3)底面回波个数N1：某时间段内，下层板底面回波幅值高于预设阈值(X1)，即为一个底面回波。

(4)中间回波个数N2：某时间段内，中间面回波幅值高于预设阈值(X2)，即为一个中间面回波，合格焊点一般N2=0。

2 有限元模型建立

2.1 基于超声波焊点检测的有限元分析

在时域分析中，有很多种方法求解超声波的传播问题，如中心差分法、Houbolt法、Newmark法、Wilson-θ法等，本文采用显式中心差分法进行求解，该方法用两步长的差分公式来表示位移向量对时间的导数，即

(4)

(5)

将式(4)、式(5)代入t时刻有限元方程[11]，得

(6)

式中,M、C、K、Ft分别为焊点样件的质量、刚度、阻尼系数及载荷矩阵。

从式(4)中可以看出由已知向量Xt及Xt-Δt可解出Xt+Δt，在计算的第一步，即t=0时刻，需要知道X-Δt的值。可以从式(4)中解出X-Δt，代入式(5)，整理后得

(7)

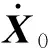
(8)

中心差分法计算过程比较简单，特别是当系统质量和阻尼矩阵为对角阵时，式(6)是一组相互独立的方程，求解过程可进一步简化。式(8)中参数M、C、K、Ft=0分别对应焊点样件的质量、刚度、阻尼系数及载荷，所以有必要建立焊点有限元模型，探究超声传播衰减情况。

2.2 焊点模型建立

本文对某厂家几款汽车白车身板材的材料类型、厚度及质量分数进行了统计分析，统计结果如表1所示。由表1可知，BLD是白车身选用最多的材料类型，常用的材料厚度依次为0.8，1.2，1.0，0.7，1.8，1.5，1.4，2.5，2.0，0.6，0.5 mm。

表1 车身板材厚度、材料类型及百分比

本文又对车身关键区域两层板焊点组合进行了统计，统计结果显示两层板样件厚度组合主要为1.4 mm×1.4 mm、0.8 mm×1.2 mm、0.8 mm×1.0 mm及1.0 mm×1.2 mm，四种厚度组合板占比达到了所有钣金件组合的60%以上。根据以上统计分析结果，针对厚度组合为1.4 mm×1.4 mm的样件类型进行仿真及实验分析。

影响焊核形成的因素较多，如焊接电流、电极压力及焊接时间等，焊点模型的准确性对仿真结果的准确性有很大影响，本次研究对焊点模型的建立步骤如图1所示。根据统计结果制作焊点样件，每组焊点样件焊接过程中，利用控制变量的思想按照一定的顺序调整焊接电压、电流及电极压力，最终得到不同质量类型的焊点，如图2所示。

图1 有限元模型建立流程图Fig.1 The flow chat of finite element model building

(a)1.4 mm×1.4mm (b)1.4 mm×1.4mm 厚度部分样件 各参数样件图2 制作样件示意图Fig.2 Diagrammatic sketch for making samples

焊点的外部参数包括焊核的形状、厚度、长度等外观尺寸。本文利用金相实验，求取平均值及标准差的方式计算得到准确的焊点外部参数。通过金相实验统计计算出1.4 mm×1.4 mm厚度组合焊核的长度、厚度等信息，结合各种缺陷焊核的特点，对应焊核有限元模型的尺寸信息如表2所示。

表2 各类型焊点外部参数Tab.2 The external parameters of the various types of welding spot mm

如果不考虑超声波在介质中衰减，则纵波在声速轴线上的声压分布表达式为

(9)

式中,ρ、c分别为介质的密度和声速；u0为源表面质点振动速度；R为超声波探头直径；λ为声波在介质中的波长；a为声束轴线上一点与声源的距离。

但由于超声波在板材中传播存在衰减[12](散射衰减和吸收衰减)，因此声压衰减规律可用下式表示：

(10)

α=αa+αs

(11)

式中，p0为入射到材料界面上的声压；p为超声波在材料中传播一段距离x后的声压；α为衰减系数;αa为只与超声波频率有关的吸收衰减系数;αs为与晶粒直径(d)和波长(λ)有关的散射衰减系数。

αs、d、λ之间有以下三种关系：

(12)

式中,c2、c3、c4为常数；F为各向异性因子;f为超声信号频率。

由此可见，由于焊接参数以及人为因素的影响，焊点内部晶粒及各向异性会产生不同的结果，从而影响到超声波的散射衰减系数αs。

由式(10)、式(11)可以得到：

(13)

式中，pn、pm为第n、第m次底面回波幅值；T为超声波在样件中传播一个焊点厚度所需要的时间。

在建立焊点CAE模型时，需要对模型的材料属性进行赋值，材料阻尼是影响超声瞬态响应的最主要因素。由于测试得到的焊点超声波回波信号只能反映信号衰减，无法直接得到焊核及板材的阻尼信息，因此需要利用超声设备测试多组焊点参数的回波信号，求出超声衰减系数。同时在仿真模型中给板材及焊核赋予一定大小的阻尼系数，通过仿真分析求得相应的衰减系数。最后进行拟合计算，得到焊点有限元模型准确的阻尼系数。具体方法如下：

(1)利用GE超声波设备对50组未经焊接的1.4mm厚度样件进行检测，并根据所得结果求得超声波在样件中的衰减系数α1；

(2)建立1.4 mm单层板样件有限元模型，给样件的结构阻尼k赋初值范围为0～0.1，每个k值间隔为0.01,对各个模型求解,计算出各个仿真模型对应的衰减系数α2～α12。

(3)从α2～α12中取最接近衰减系数α1的对应阻尼值kt，定为焊点母材的结构阻尼。计算分析求得kt为0.02。

(4)建立1.4mm×1.4mm焊点组合的CAE模型，对母材阻尼kt赋值，基于焊核结构阻尼经验值(0.1)前后取若干数值分别给焊核阻尼赋值，并分别求出对应的信号衰减系数，具体数值如表3所示。根据表3，拟合出焊核结构阻尼与超声信号衰减系数的关系,如图3所示，结合检测计算得到的合格焊点衰减系数，计算得到合格焊核的结构阻尼为0.12。

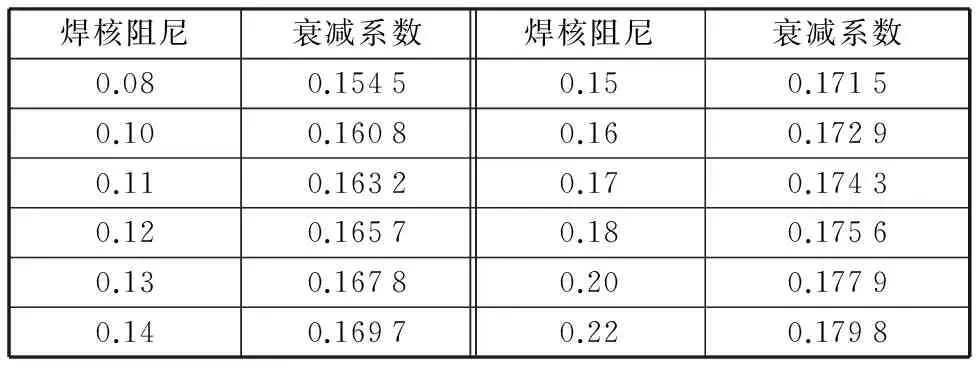
表3 焊核阻尼及对应的信号衰减系数Tab.3 Welding core damping and corresponding signal attenuation coefficient

图3 阻尼-衰减系数关系曲线Fig.3 The relationship curve between the damping coefficient and the attenuation coefficient

(5)在Hypermesh中划分网格，合格焊点有限元模型如图4所示，该模型包含上层板、下层板以及焊核，并且上下层板均有一层0.20 mm的压痕，其中焊点将上层板与下层板连接在一起，所以在有限元模型中采用节点重合的方式。

图4 1.4 mm×1.4 mm焊点组合CAE模型Fig.4 The CAE model of 1.4 mm×1.4 mm welding spot

2.3 理想情况下焊点仿真质量验证

为了验证焊点有限元模型的准确性，对建立的有限元模型用Nastran计算分析，最后导入MATLAB中进行曲线的合并优化，得到各类型焊点的超声回波曲线的图像。

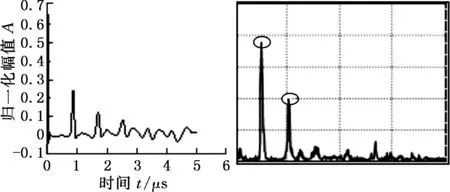
合格焊点模型仿真曲线和超声设备检测结果如图5所示，根据回波信号衰减曲线可以分别求出仿真信号曲线及检测信号曲线的衰减系数α、α′，结果显示α′≈α，并且从仿真曲线与设备检测信号可以看出,合格焊点仿真曲线与检测信号回波衰减特征趋势基本一致：均具有三个底面回波，仿真与检测的超声信号回波间距分别为0.79μs和0.82μs，且均未出现中间回波的共同特征，验证了仿真模型的准确性。

(a)合格焊点仿真曲线 (b)合格焊点实际检测波形图5 合格焊点CAE仿真与实际检测波形图Fig.5 The CAE simulation and practical detection waveform diagram of qualified welding spot

(a)过烧焊点仿真曲线 (b)过烧焊点实际检测波形图6 过烧焊点CAE仿真与实际检测波形图Fig.6 The CAE simulation and practical detection waveform diagram of burn-through welding spot

过烧焊核模型仿真曲线和超声设备检测结果如图6所示。焊接时由于焊接电流过大或通电时间过长，导致金属熔化形成焊核的过程中，形成的焊核区域比正常焊点范围更大，焊点厚度也相应增大，在短时间冷却时形成的金属晶粒较大，焊点内部的阻尼增大。通过图6可以看出，仿真信号能够很好地反映出超声信号在过烧焊核中传播时散射衰减大，衰减速度快的特征。对比图6和图5可知，过烧焊核相对于合格焊核的底面回波个数减少，回波衰减率偏小。

薄焊核模型仿真曲线和超声设备检测结果如图7所示。焊接时由于电极加载时间短或者焊接电流偏小，导致熔核厚度小，粗晶粒区域变小。对比图7所示的仿真和测试曲线可知，焊核阻尼明显大于母材阻尼，超声信号衰减趋势减慢，仿真信号与测试信号均出现多个底面回波的共同特征，较合格焊点图5中信号仿真曲线，薄焊核超声信号衰减率较高，底面回波个数明显增多。

(a)薄焊核仿真曲线 (b)薄焊核实际检测波形图7 薄焊核CAE仿真与实际检测波形图Fig.7 The CAE simulation and practical detection waveform diagram of the thin welding spot

图8为小焊核模型(熔核直径小)仿真曲线与超声设备检测波形图，对比图8a、图8b可以看出，回波信号均出现中间回波，且中间回波峰值刚好处在底面回波峰值之间的中间位置。这是因为焊核直径小，在下层板底面焊核两端产生了回波，

(a)小焊核仿真曲线 (b)小焊核实际检测波形图8 小焊核CAE仿真与实际检测波形图Fig.8 The CAE simulation and practical detection waveform diagram of the little welding spot

随着直径的减小，第一次中间回波峰值逐渐增大，下底面回波个数理论上是减少的，但由于偶数次中间回波与奇数次底面回波的叠加，图示底面回波个数适中。

从焊点的回波曲线图中可以看出底面回波个数及中间回波个数。为了更加直观地对比各类型焊点的回波参数，表4中列出了各个仿真模型中超声特征参数的量化结果。

表4 各类型焊点超声参数Tab.4 The ultrasonic parameters of the various types of welding spot

3 数据验证及复杂曲面检测分析

3.1 焊点质量识别结果

为验证理论分析以及仿真分析的正确性，本研究利用进口的Olympus设备建立了1.4 mm×1.4 mm厚度焊点质量检测的数据库，下面选取了部分样件检测数据，见表5。

表5 Olympus检测设备1.4 mm×1.4 mm样件检测数据Tab.5 The 1.4 mm×1.4 mm sample detection data of the Olympus detection equipment

从表4、表5中各类型焊点波形分析可以看出：过烧焊点的回波衰减率最小，衰减最快；小焊核焊点在两层板中间处出现中间回波；薄焊核焊点回波衰减率最大，衰减最慢。检测结果与仿真分析结果中各回波特征值一致，从数据角度说明了焊点模型的准确性。可利用此仿真方法建立准确的焊点质量标准实现焊点质量的预判，提高对焊点质量的监督。

3.2 复杂曲面焊点角度定位分析

目前可以通过多种手段确定焊点在车身的位置，但由于焊点表面是类似于圆弧的非平面，平面视觉定位机械手在角度方向上的偏差、人工检测时操作人员视觉误差以及主观判断因素带来的影响，均无法保证超声探头能够与焊点中心平面垂直。本文利用仿真模型探究主客观情况下超声探头在角度方向上相对焊点法线方向偏离一定角度(设定最小偏离角度是1°,最大偏离角度是10°)，超声信号传播衰减发生的变化及对检测结果带来的影响。

具体方法如下：对建立的焊点模型分别在X、Y方向进行加载，总载荷大小为1，载荷分配按照三角形法则进行，焊点检测角度设置在预定的区间范围(1°～10°)内。通过对模型计算分析可知，仿真结果曲线之间基本无差异，焊点质量超声波检测结果偏差极小。此结果说明：探头在空间角度方向上偏离法线方向在10°范围内，焊点质量探测结果基本无变化。因此当机械手通过视觉定位焊点质量检测时，角度方向的定位偏差及车身钣金件带来的视觉误差对检测结果带来的影响不大，这为研究焊点自动检测设备提供了依据。

为验证上述结论，本次研究通过自制的白车身焊点自动化探测设备进行实验验证,如图9所示。首先用机械手夹持探头，然后对目标焊点进行拍照，根据视觉图像处理的方法，得到焊点中心点精确的位置坐标，并将超声探头通过末端执行器运动调整到相应位置，记录焊点质量的检测结果；接下来依次调整机器人末端执行器在角度方向的位置，得到的检测结果如表6所示。

图9 机械手焊点质量检测定位Fig.9 The welding spot quality detection positioning of mechanical arm

由表6可见，超声波探头在角度方向的探测可在一定范围内具有结果的一致性，焊点检测的结果能够在保证精确探测位置的前提下，抵抗人为主观误差以及机械手在角度方向上定位偏差能力较强，也说明了超声探头在角度方向的容错能力较强。

表6 探头偏转角度及相应结果

4 结论

(1)通过焊点的金相实验得到车身焊点的基本尺寸信息，通过超声波传播衰减特性得到了焊核板材的内部阻尼，建立了焊点仿真模型。

(2)对不同类型焊点进行有限元仿真，仿真信号特征参数与实验结果吻合度较高，说明了仿真模型建立方法的准确性和有效性。仿真模型在焊点质量检测中可以根据超声波时域信息对焊点质量进行预判。

(3)通过在实际工况下控制机械手夹持探头偏转一定角度，证明了曲面焊点检测结果在一定角度范围内对检测结果影响很小，为实现焊点的自动化检测提供了支撑。

[1] 牛济泰,王式正.焊接基础[M].哈尔滨:黑龙江科技出版社,1986. NIU Jitai, WANG Shizheng. Welding Base[M]. Harbin: Heilongjiang Science and Technology Press,1986.

[2] 刚铁,张锦,沈春龙.点焊质量监控与检测的现状及发展[J].航天工艺,1998(5):51-55. GANG Tie, ZHANG Jin, SHEN Chunlong. The Present Situation and Development of Spot Welding Quality Monitoring and Testing [J]. Space Technology,1998(5):51-55.

[3] 王俊强. 基于超声回波特征的电阻点焊接头缺陷识别[D].上海：上海交通大学，2006. WANG Junqiang. Defect Identification of Resistance Spot Welding Joint Based on Ultrasonic Echo Characteristics [D]. Shanghai: Shanghai Jiao Tong University,2006.

[4] 刘登第.无损检测模糊理论及其应用研究[D].北京：北京航空航天大学,1999. LIU Dengdi. Nondestructive Testing Theory and Its Application Research [D].Beijing: Beihang University,1999.

[5] 陈丹,肖会芳,黎敏,等. 金属材料内部非金属夹杂超声检测的数值模拟[J]. 工程科学学报,2015,37(7):942-949. CHEN Dan, XIAO Huifang, LI Min, et al. Numerical Simulation of Ultrasonic Testing for Non-metallic Inclusions in Metallic Materials[J]. Chinese Journal of Engineering,2015,37(7):942-949.

[6] YU J M, ZHANG Z. Rsearch on Feature Extraction for Ultrasonic Echo Signal Based on EEMD Approach[J]. Applied Mechanics and Materials,2013,321/324:1311-1316.

[7] 于建明.基于时频分析方法的超声回波信号特征提取研究[D].呼和浩特：内蒙古大学,2013. YU Jianming. Rsearch on Feature Extraction for Ultrasonic Echo Signals Based on Time-frequency Analysis Methods[D]. Hottot: Inner Mongolia University,2013.

[8] MORBIDUCCI U, TURA A, GRIGIONI M. Genetic Algorithms for Parameter Estimation in Mathematical Modeling of Glucose Metabolism[J]. Computers in Biology and Medicine,2005,35(10)：862-874.

[9] 张崧，彭光俊，史红. 超声法检测金属薄板点焊接头质量研究[J]. 哈尔滨工业大学学报,2003,35(11)：1392- 1394. ZHANG Song, PENG Guangjun, SHI Hong. Ultrasonic Inspection of Spot Welding Quality [J]. Journal of Harbin Institute of Technology,2003,35(11)：1392- 1394.

[10] 聂昕,郭志福,何智成,等. 基于盲反卷积和参数化模型的超声参数估计[J]. 仪器仪表学报,2015,36(11):2611-2616. NIE Xin, GUO Zhifu, HE Zhicheng, et al. Parameters Estimation of Ultrasonic Echo Signal Based on Blind Deconvolution and Parameterized Model[J]. Chinese Journal of Scientific Instrument,2015,36(11):2611-2616.

[11] LIU G R, QUEK S S.The Finite Element Method-A Practical Course[M].England:Elsevier Science Ltd.,2003.

[12] 邵泽波.无损检测技术[M].北京:化学工业出版社,2003. SHAO Zebo. Nonivasive Testing Technology [M]. Beijing: China Machine Press,2003.